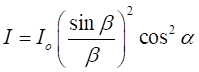DOING PHYSICS WITH MATLAB

MATLAB RESOURCES FOR

INTRODUCTION TO QUANTUM MECHANICS

3rd Edition

David J Griffiths & Darrel F Schroeter

                  

Ian Cooper

matlabvisualphysics@gmail.com

 

CHAPTER 1

THE WAVEFUNCTION

STATISTICAL INTERPRETATION

WAVE PARTICLE DUALITY

 

 

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

   GitHub

   Google Drive

 

diffraction_1slit.m

                                Simulation of the diffraction of visible light through a single slit.

diffraction_2slit.m

        Simulation of the diffraction of visible light through a double slit.

diffraction_particle.m

        Animation of the diffraction of a stream of particles passing through a double slit.

ColorCode.m

        Returns the color appropriate to a supplied wavelength. Is it assumed the supplied lambda is within the range 380-780 nm. Smaller or higher values are set notionally to the extreme values. All input measurements are in metres.

interference.m   interference1.m

          Simulation of the interference pattern of water waves passing through a pair of slits.

 

Are electrons particles or waves ?

 

LIGHT BEHAVING AS WAVES

When light passes through very narrow apertures and falls on a screen, a diffraction / interference pattern consisting of a band of bright and dark regions is observed. The brightness (intensity) of light detected on the screen is proportional to the square of the amplitude of the wave. For a plane wave incident upon an aperture, we observe Fraunhofer diffraction when the screen distance is much larger than the width of the apertures.

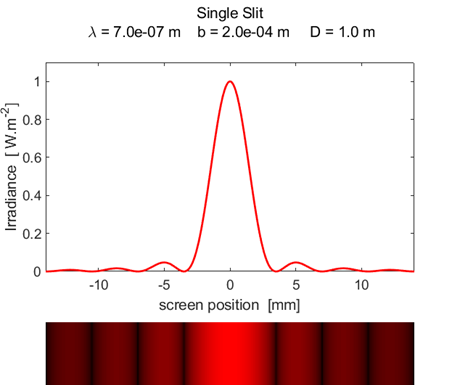
The intensity of light reaching the screen for a single slit is given by the equation

        (1)      

 where

          I        intensity of the light [W.m-2]

          Io       maximum intensity [W.m-2]

                 [rad]

          k          [rad.m-1]

               wavelength of light [m]

          b       slit width [m]

                direction to point on screen from aperture [rad]

                  

          x        position of screen [m]

          D       aperture screen distance [m]

 

 

The script diffraction_1slit.m can be used to show the diffraction pattern for a single aperture. The graphical output of the Script (figure 1) shows a graph of the intensity calculated by equation 1 and a two dimensional plot showing the bright and dark bands that would be observed. The wavelength (380 – 780 nm) and width of the aperture can be changed in the Script to observe the changes in the diffraction pattern. The script diffraction_1slit.m calls the function ColorCode.m so the color of the display corresponds to the color associated with the wavelength of the light. The maximum intensity has been normalized to 1 W.m-2.

 

 

Fig. 1.   Fraunhofer diffraction from a single slit.    diffraction_1slit.m

 

 

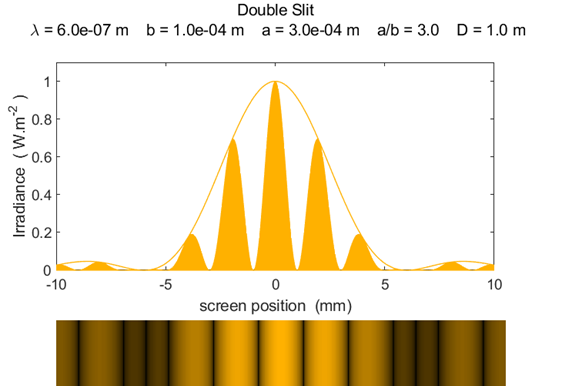
The intensity of light reaching the screen from a double slit is given by the equation

        (2)      

 

where            slit separation   a  [m]         [rad]                

 

Figure 2 shows the graphical output for a double slit using the Script diffraction_2slit.m. In the Script, you can vary the wavelength, slit width and slit separation and observe the resulting changes in the diffraction pattern. The maximum intensity has been normalized to 1 W.m-2.

 

 

Fig. 2.  Fraunhofer diffraction from a double slit (= 450 nm).     diffraction_2slit.m

 

 

PARTICLES BEHAVING AS WAVES

Waves are a mechanism for transferring energy via some kind of vibration without any matter being transferred. One characteristic of waves but not of particles, is that, diffraction / interference is observed as shown in figures 1 and 2 when a wave passes through an aperture. However, in experimental arrangements analogous to the two slit interference for light, when a beam of electrons is incident upon a biprism (mimics two slits for light as the electrons can travel in two paths around a filament) and are detected upon a screen, an interference pattern is observed. When a few electrons hit the screen, no noticeable pattern is discerned as shown in figure 3.

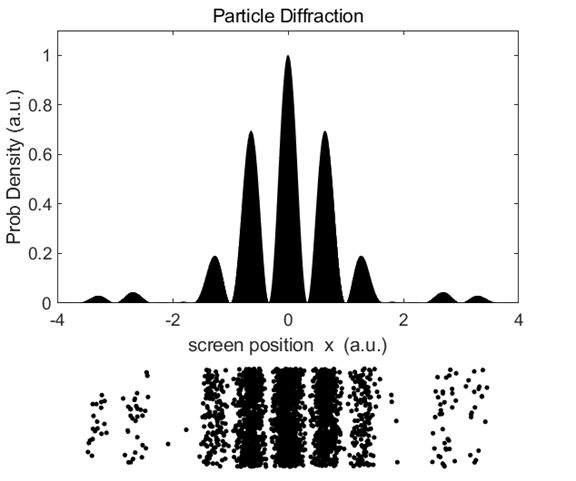
Fig. 3.   Pattern formed by 2000 electrons on passing through the equivalent of a double slit. diffraction_particle.m

 

 

However, for much longer exposures involving 80000 plus electrons, a very distinctive two slit diffraction pattern is clearly observed as shown in Figure (4). Running the Script diffraction_particle.m you can include a pause statement to animate the individual electrons hitting the screen to show how the interference pattern develops.

 

        Fig. 4.     Pattern formed by 80000 electrons on passing through the equivalent of a double slit. As more and more electrons hit the screen a two slit interference pattern develops. diffraction_particle.m

 

 

The electrons are individual particles when they strike a single point on the detection screen, but the distribution of the points on the screen gives an interference pattern which can only be attributed to a wave phenomenon. Hence, we can only conclude that electrons have this dual nature – they behave as particles or as waves. We can’t predict where a single electron will arrive on the screen. We only know the probability of where an electron will strike. This behavior is typical of the quantum world and is a good example of the interplay between indeterminism and determinism.

 

The electron is represented by a mathematical function called the wavefunction   which is a function of the position of the electron and time. The evolution of the wavefunction for a single electron is governed by the Schrodinger’s equation. However, this wavefunction is a complex quantity and can’t be measured directly. From it we can find the probability of locating the electron at some instant. The probability density is proportional to the real quantity.

 

We can now interpret the irradiance given by equation 2 as a probability density for the electron striking the screen and the area under the curve being proportional to the probability of finding the electron. For a one-dimensional system, the probability of finding an electron between x1 and x2 at time t is given by

        (3)      

 

and for the two slit example, the probability of hitting a pixel at position (x, y) on the detection screen at time t is

        (4)      

 

where A is the area of the pixel.

 

We can’t predict where a particular electron will strike the screen but the pattern formed by many electrons is predicted by the Schrodinger equation which tells how  spreads out from the slit to the screen. When a single electron leaves the slits and just before it strikes the screen, its wavefunction is spread out over a wide area which would cover many pixels, but only one pixel is triggered to respond, no other pixels respond. When a single pixel is triggered we can interpret this in terms of news spreading out instantly from the responding pixel, telling all other pixels not to respond. This is an example of quantum non-locality – what happens at one place affects what happens at other places in a manner that can’t be explained by communication at the speed of light (maximum speed at which any information can be transmitted). We say that when the electron is detected, its wavefunction collapses. In terms of quantum physics, a particle is interpreted as an entity which is found in only one place when its position is measured. 

 

For a free particle (total energy E = kinetic energy K, potential energy U = 0) its wave nature is described by its de Broglie wavelength

        (5)      

 

where h is Planck’s constant and p is the momentum of the particle. Diffraction experiments confirm that the wavelength given by equation 5 agrees with the wavelength as measured in these experiments.

 

Classical waves and matter (particle) waves have very different characteristics. Consider, for example, the interference pattern produced by water waves passing through two slits. If one slit was blocked a cork floating on the water would simply bob up and down. For the two slits, the movement of the cork is the determined by the summation of the displacement of the two waves emerging from the slits. Upon passing through the slits the waves spread out. At some locations, the cork would move up and down with maximum displacement due to the constructive interference of the two waves. 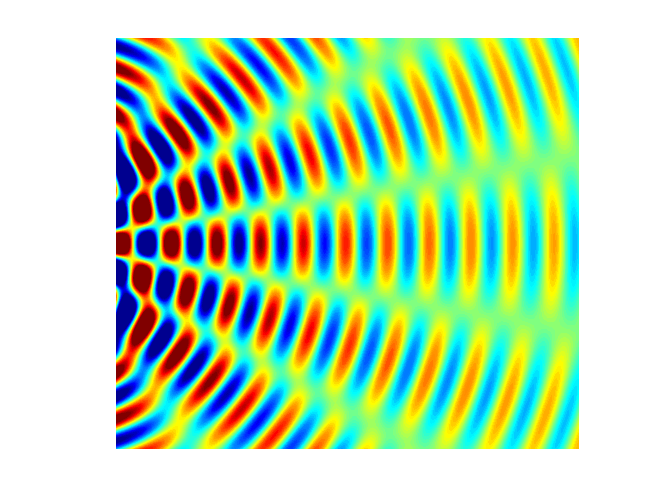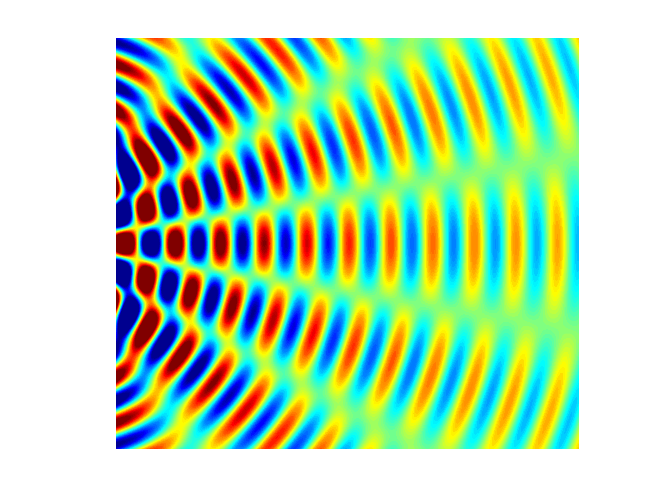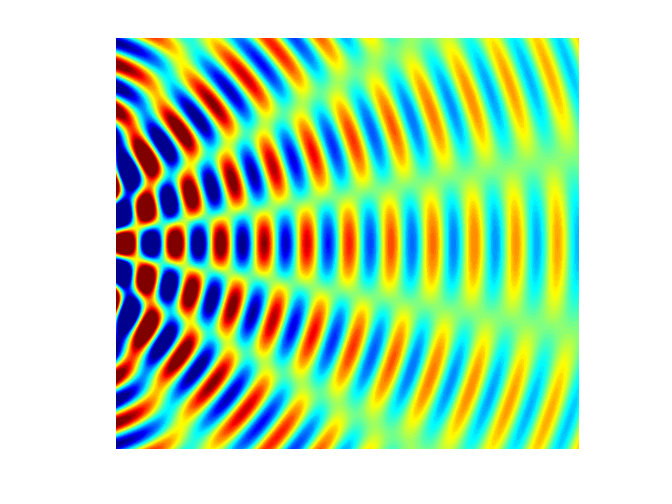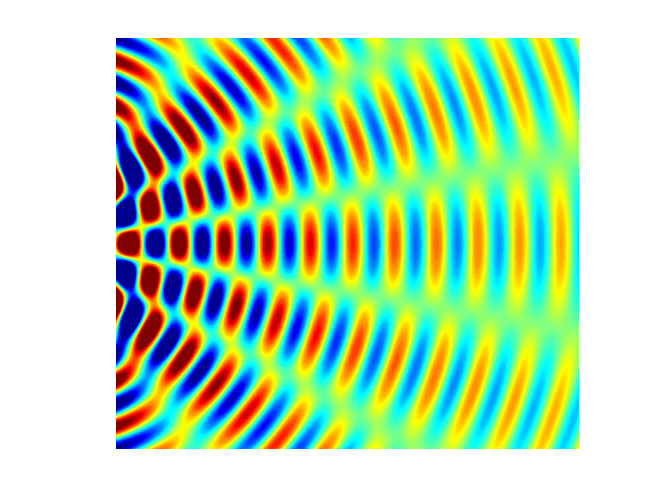At other places, the cork would remain still as the two waves cancel each other (destructive interference).  Figure 5 shows a typical interference pattern for two slits at one instant of time.


 

       

Fig. 5.     Typical two slit interference showing radiating lines for the nodes (destructive interference ) and antinodes (constructive interference). interference.m

 

The position of an electron is not known until it is measured. The electron does not spread out like the wave producing the interference pattern. The complex wavefunction gives a complete description of the electron. It is no longer sensible to think about the electron as a moving particle. tells us only the probability for finding the electron at a certain location.

 

The electrons propagate as waves (but not like classical waves) and are detected as particles – they display wave-particle duality.

 

https://stemjock.com/griffithsqm3e.htm