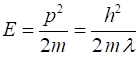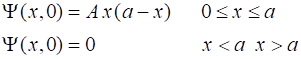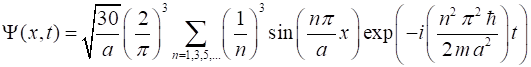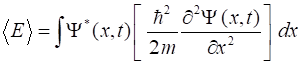MATLAB RESOURCES

INTRODUCTION TO QUANTUM MECHANICS

3^rd Edition

David J Griffiths & Darrel F Schroeter

Ian Cooper

matlabvisualphysics@gmail.com

CHAPTER 2

THE SCHRODINGER EQUATION

THE INFINITE SQUARE WELL

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

GitHub

Google Drive

simpson1d.m

QMG2B.m

Analytical solution: Animated plot for the time evolution of the wavefunction and probability density function. A plot of the wavefunction at the centre of the potential well as a function of time. Calculations of the frequency and period of the oscillation. The animation can be saved as a gif file.

QMG2BB.m

Numerical solution (finite difference time development method): Animated plot for the time evolution of the wavefunction and probability density function. A plot of the wavefunction at the centre of the potential well as a function of time. Fourier transform of the wavefunction at the centre of the potential well. Calculations of the frequency and period of the oscillation.

Calculation of the total energy E

Expectation value

Frequency

Wavelength & momentum

Uncertainty principal calculations

Expectation values

Standard deviations

The animation can be saved as a gif file.

I will only consider the Griffith Example 2.2, but in much more detail than is required from the question. The techniques and methods used in my solution will enable you to do most of the examples and problems in the section 2.2 The Infinite Square Well.

Griffith Example 2.2

A particle in the infinite square well has the initial wave function

for some constant A. Find .

After much tedious algebra, the solution for the wavefunction is

However, using the Matlab Script QMG2B.m, a greater insight to the solution can be gained by an animation of the wavefunction and probability density function. The width of the well is a = 1.0000 nm and the particle is an electron trapped inside the potential well. The Script checks that the wavefunction is correctly normalized and computes the period of the major peak in the wavefunction (n = 1).

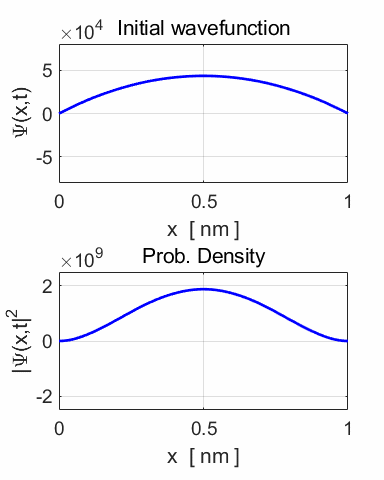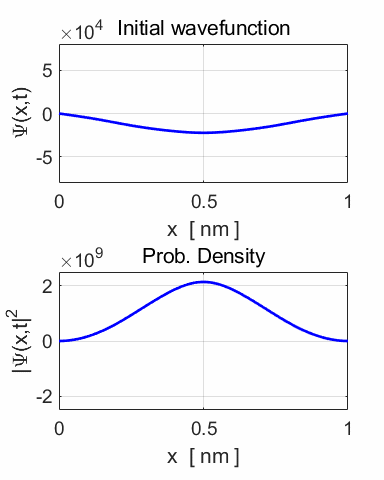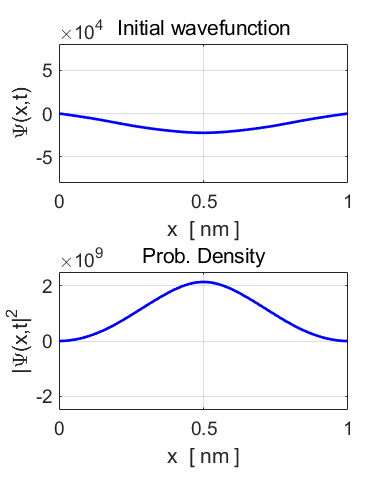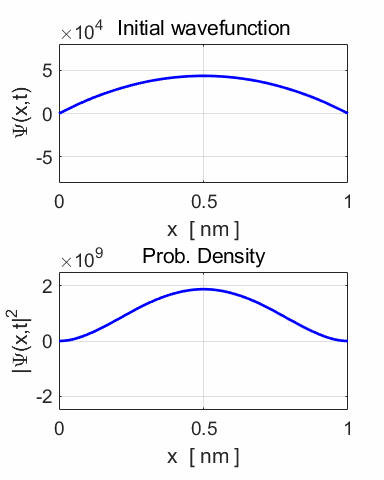
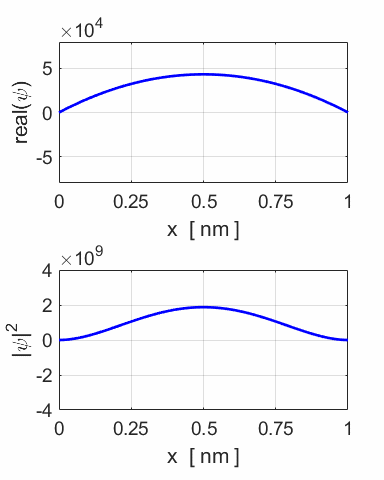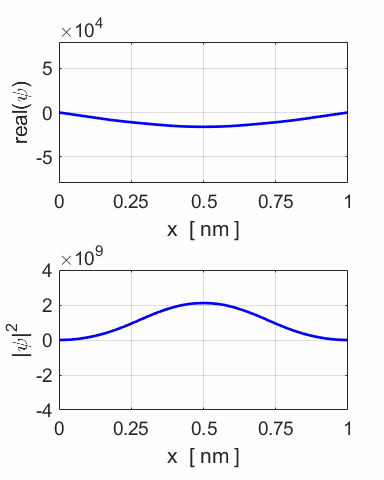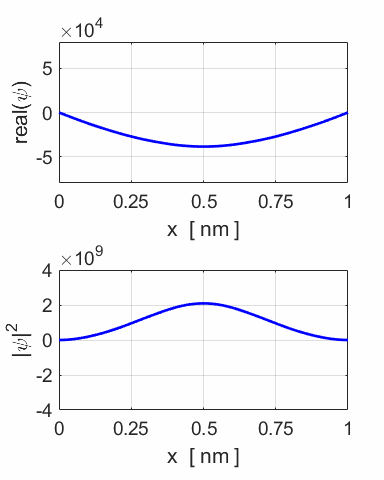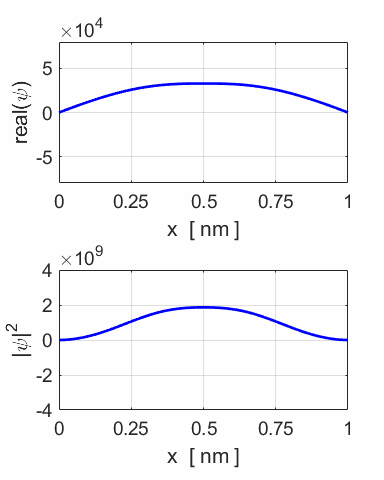
Animation of the wavefunction and the probability density function.

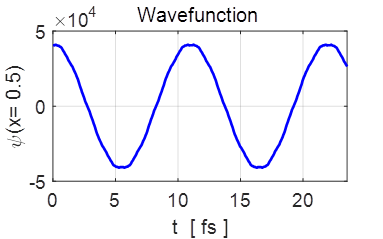
The periodic motion of the wavefunction at the centre of the potential well.

Notice the wobbles that occur in the functions, especially near the extreme positions.

Left graph QMG2B.m (analytical solution)

Right graph QMG2BB.m (numerical solution)

The angular frequency , frequency f and period P for this motion where n = 1 are

ang. frequency(n = 1) = 5.7129e+14 rad/s

period(n = 1) = 10.9982 fs

frequency(n = 1) = 9.0924e+13 Hz

An alternative way to solve this problem is by numerically solving the Schrodinger equation using the finite difference time development method (FDTD) for the given initial value of the unnormalized wavefunction using the Script QMG2BB.m. This has the advantages of not doing all the tedious algebra and it is a simple matter to change the Script for a different initial wavefunction. The analytical solution and the numerical solution give results that are basically the same. However, the wobbles are more evident in the analytical solution.

With the Script QMG2BB.m we can perform a Fourier transform on the time variation of the wavefunction at the centre of the well to estimate the frequency and period of the oscillation.

Fourier transform

fpeak = 9.23e+13 Hz

period = 10.84 fs

The period of oscillation calculated by both methods are in good agreement with each other

(P_A = 11.0 fs P_N = 10.8 fs).

We can also estimate the total energy of the system and since the potential energy is zero, the total energy equals the kinetic energy of the electron. The wavelength is approximately equal to twice the width of the well.

Wavelength = 2.0000 nm