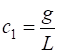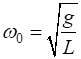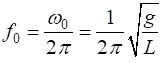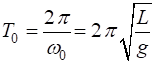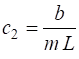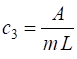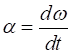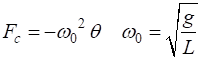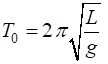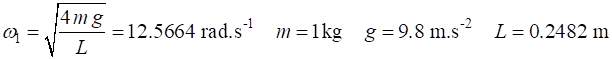DOING PHYSICS WITH MATLAB

DYNAMICS OF OSCILLATING AND CHAOTIC SYSTEMS

RIGID PENDULUM

 

Ian Cooper

 

matlabvisualphysics@gmail.com

 

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

 

chaos07A.m

Runga-Kutta method for solving the equation of motion for a rigid pendulum with damping and applied external driving force acting on the system.

chaos07AB

A bifurcation diagram for the driven damped pendulum.

 

 

 

INTRODUCTION

 

The system we will simulate is a rigid pendulum where a mass m is attached to a rigid massless rod so that the centre of mass is a distance L from a frictionless pivot. There is viscous damping of the motion and an externally applied sinusoidal driving force acting on the pendulum. The system is constrained to move in a plane. 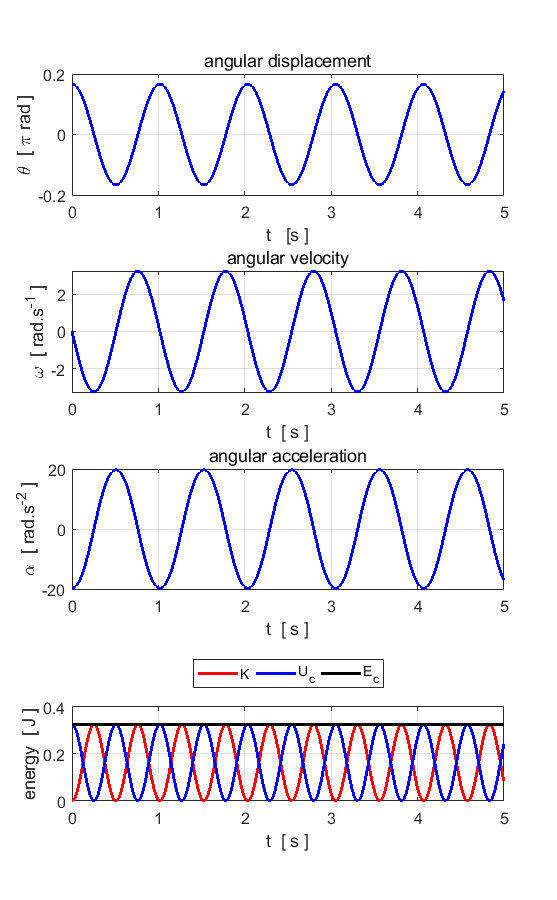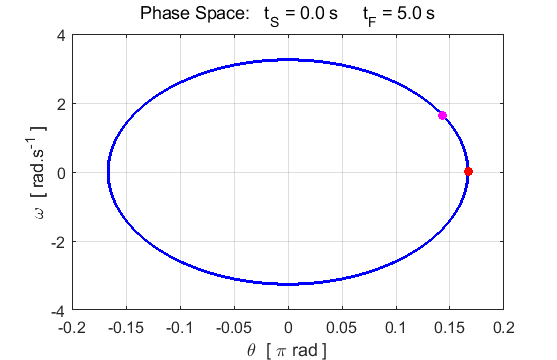The net force acting on the system is the resultant force due to the gravitational force ; a viscous drag force  and an externally applied sinusoidal driving force .  The motion is described in terms of the angular displacement , the angular velocity , and the angular acceleration .

 

The equation of motion of this system is governed by the equation of motion

      (1)      

where  is the torque about the pivot point, and   is the moment of inertia about the pivot point. Hence, the net torque acting on the system produces the angular acceleration  

                 

 

      (2a)             

 

      (2b)             

                  

where

           determines the natural frequency  of the rigid pendulum for small amplitude

                        oscillations

                       angular frequency      

                       natural frequency   

 

                       period                         

 

               determines the strength of the viscous damping

               determines the strength of the applied external driving force

 

               angular frequency of the driving force

 

This system is called a non-linear dynamical system since the differential equation describing the system contains non-linear terms.

 

Equation 2 is the equation of motion that is solved using the Runge-Kutta method.

 

The Matlab variables for the angular displacement, angular velocity and angular acceleration are:  

 

In the Matlab script chaos07A.m the equation of motion (equation 2) is given in terms of the global variable c which is a matrix of four elements. The differential equation (equation 2) is given by the Matlab function

 

% Equation of motion

function  y = fn(t,x,v)

  global c

  y = - ( c(1)*sin(x) + c(2)*v + c(3)*cos(c(4)*t) ) ;

end

   

 The default value for the parameters: m, g, T0, L, c(1) are specified in the CONSTANTS and DEFAULT section of the script chaos07A.m.

 

The INPUT section of the script chaos07A.m is used to set the values:

    nT                               number of time steps

   tMax                           simulation time

   tS and tF                    start and finish times for displaying the graphical output

  c(2), c(3) and c(4)     differential equation coefficients

  x(1) and v(1)             initial values for angular displacement and angular velocity

  

The Runga-Kutta algorithm computes the angular displacement and angular velocity at each time step. Then the angular acceleration, kinetic energy, potential energy and total of the energy of the system are calculated.

             acceleration                         

             restoring force                              (conservative force)                                                

             kinetic energy                      

            

            potential energy (conservative force  )

                                                                  

           

           total energy                         

 

         potential                               

 

We can define a potential function V associated with the conservative force FC acting on the system. The potential V is the potential energy per unit mass (electric potential is the work done per unit charge).

 

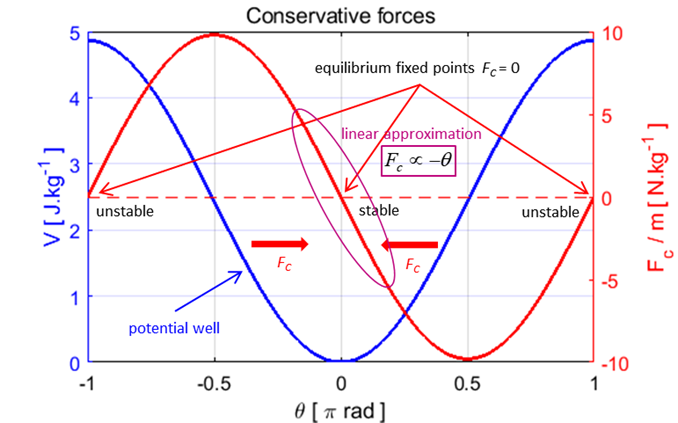
   Fig. 1.   Conservative force and associated potential curve for the rigid pendulum. 

 

The conservative force acting on the pendulum is such that it is in a direction to try and restore the pendulum to its equilibrium position at . The graph of the restoring force (conservative force) against the angular displacement is not linear but of the form . However, for small angular displacements, to a good approximation, the restoring force is a linear function of the angular displacement: .

 

There are two equilibrium positions for the pendulum. These two equilibrium points are called fixed points in chaotic dynamics. The two fixed points are:

1.    When the pendulum is hanging down from its pivot point  . This is a stable equilibrium point.

2.    When the pendulum is standing directly above the pivot point. This is an unstable equilibrium point.

 

 

SIMULATIONS     chaos07A.m

 

Simulation #1   Small amplitude, free motion of the rigid pendulum

For small amplitude oscillations, the motion of the pendulum bob is to a good approximation described by the equations of simple harmonic motion

       

 

with a natural period of oscillation

     

 

The default value for all simulations is . The numerical solution of the differential equation for the free motion of the rigid pendulum agrees with this prediction as shown in figure 2.

 

Input parameters

         nT = 801     tMax = 5     tS = 0     tF = t(end)

         c(2) = 0     c(3) = 0     c(4) = 0           zero damping and zero applied force

         x(1) = /6     v(1)  = 0                      initial angular displacement and angular velocity

 

Graphical outputs

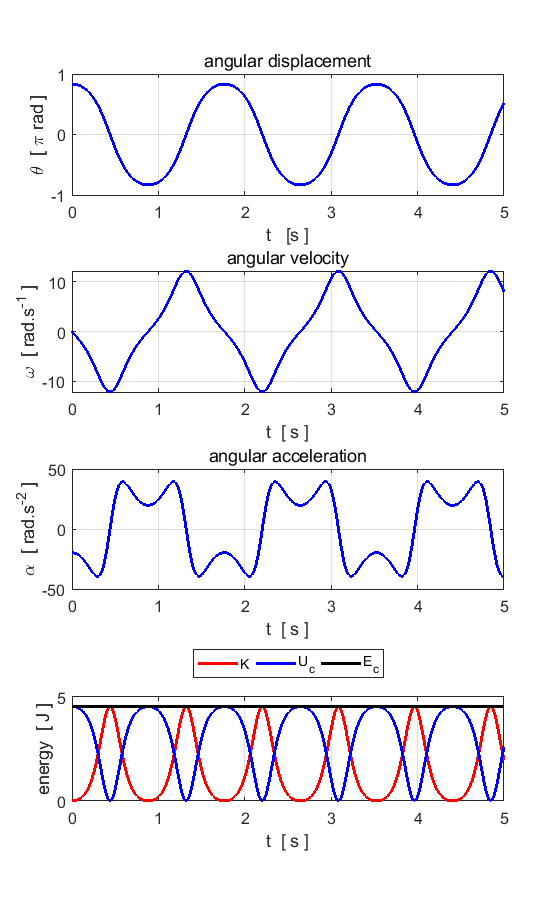
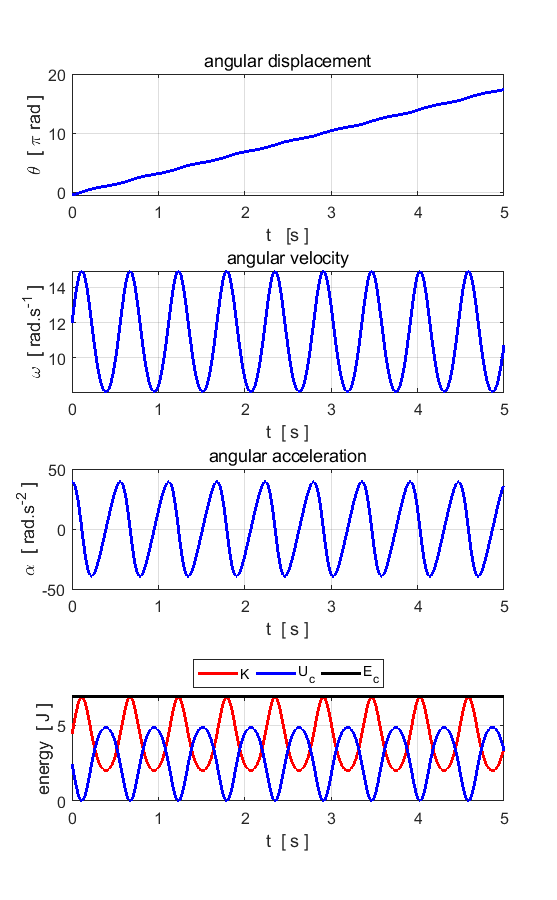
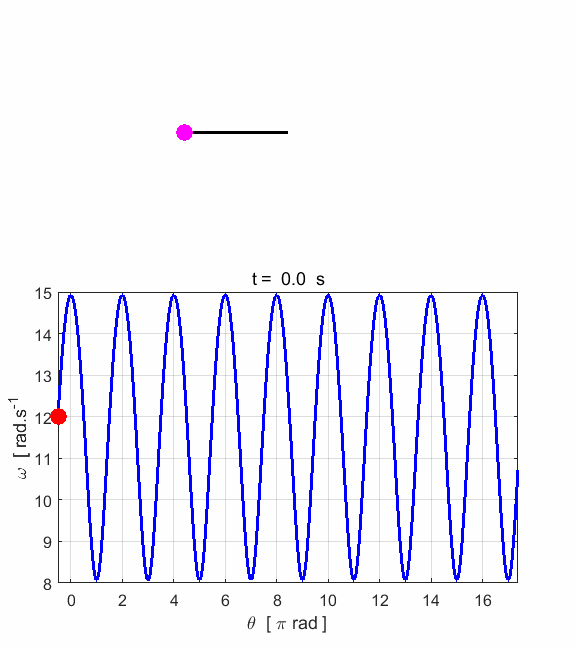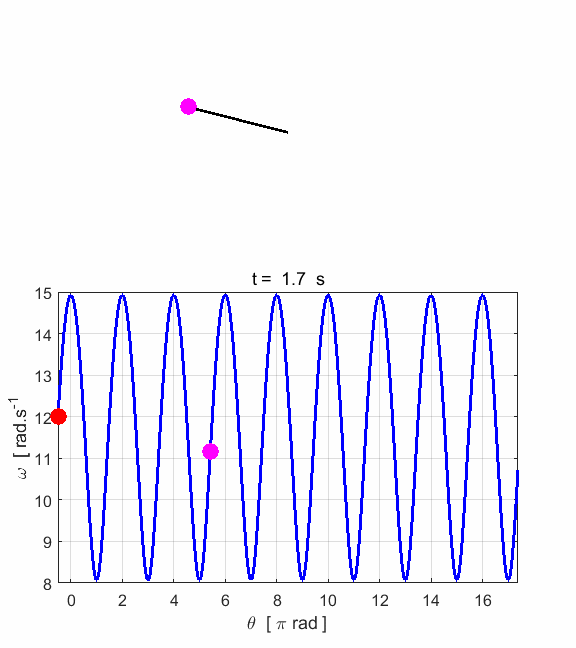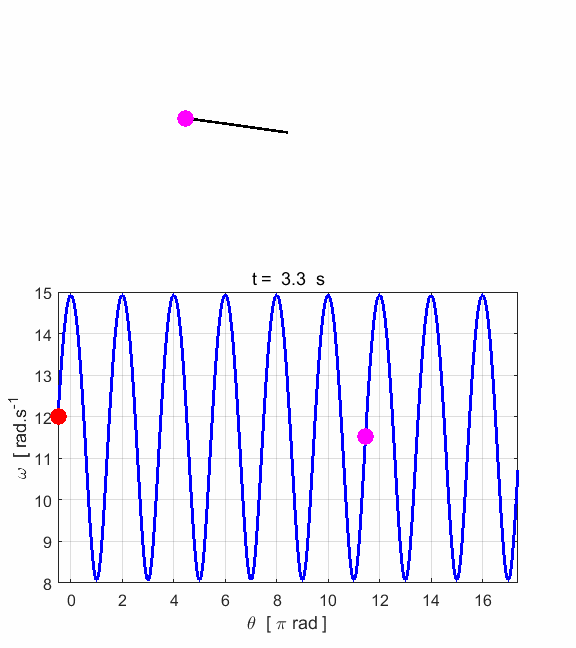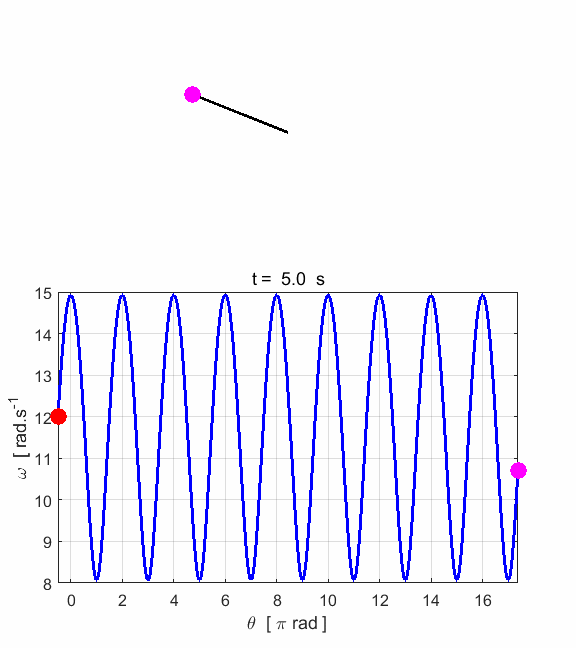
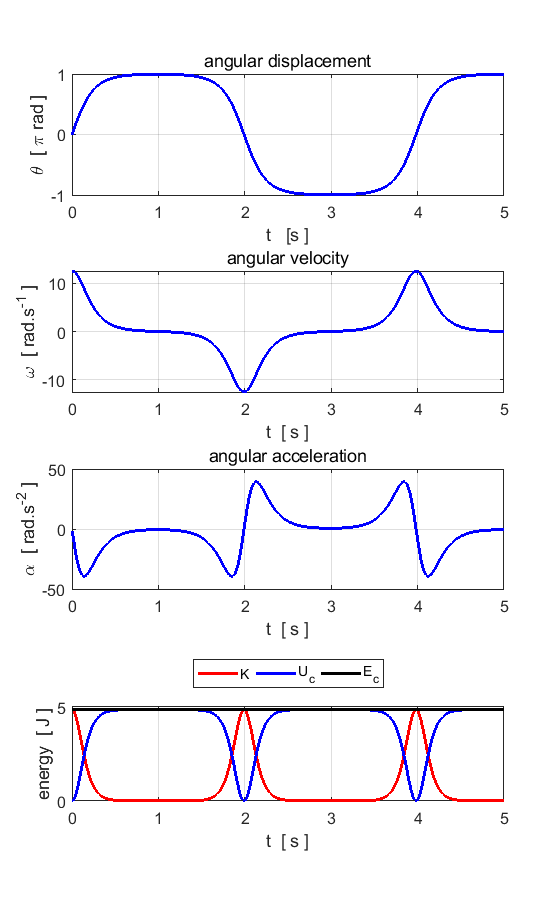
Fig. 1.1.   The motion of the pendulum bob is to a good approximation simple harmonic motion with a period of ~1.0 s. The total energy is conserved. The potential curve (figure 1) is approximately a parabolic function of angle for small angular displacements, .

 

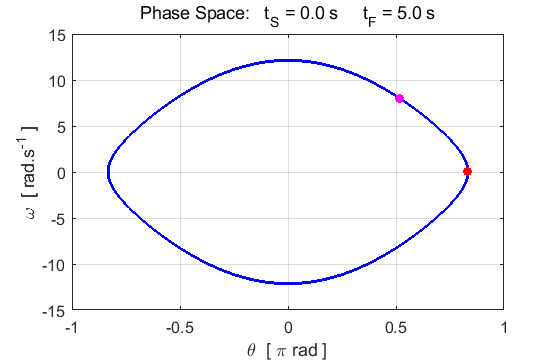
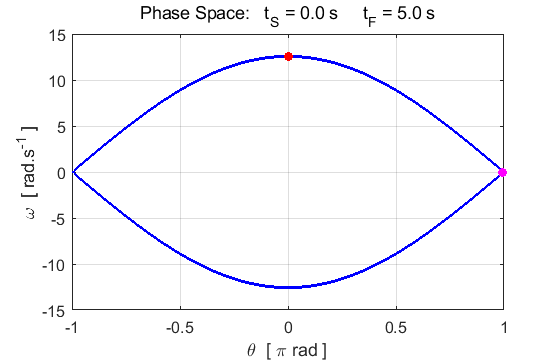
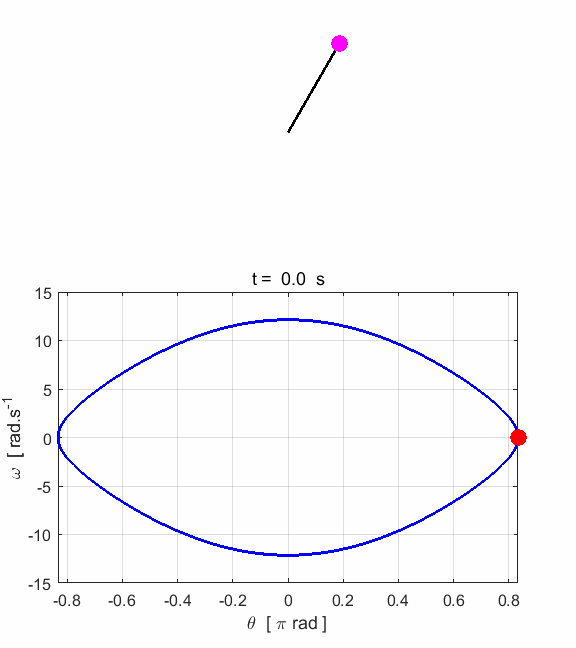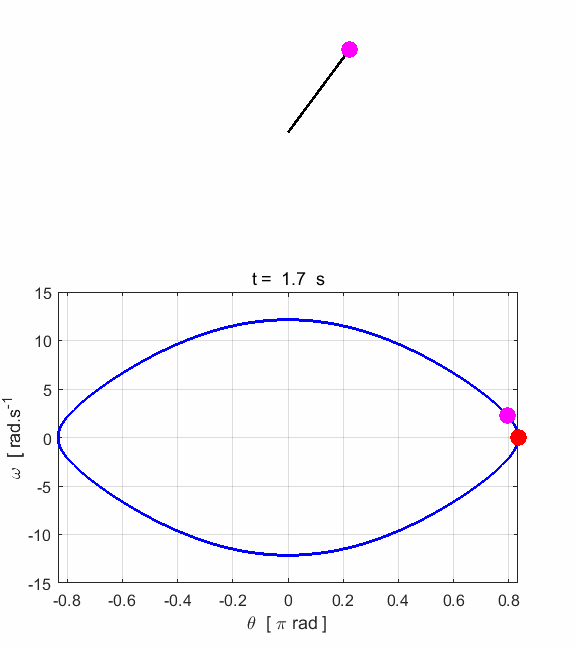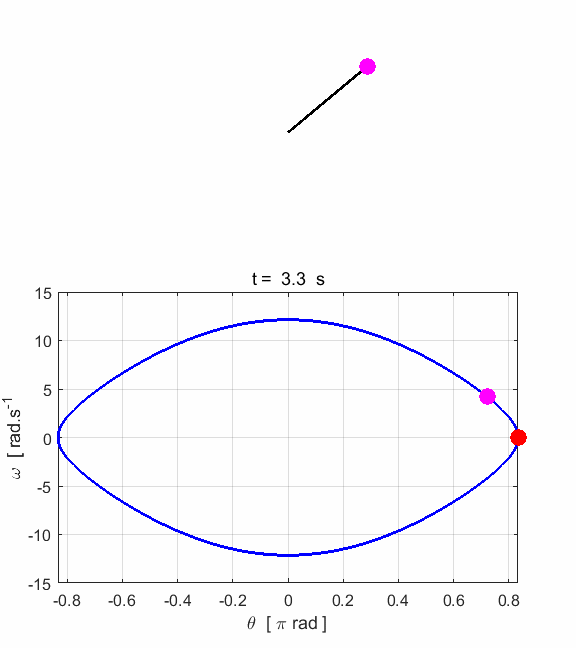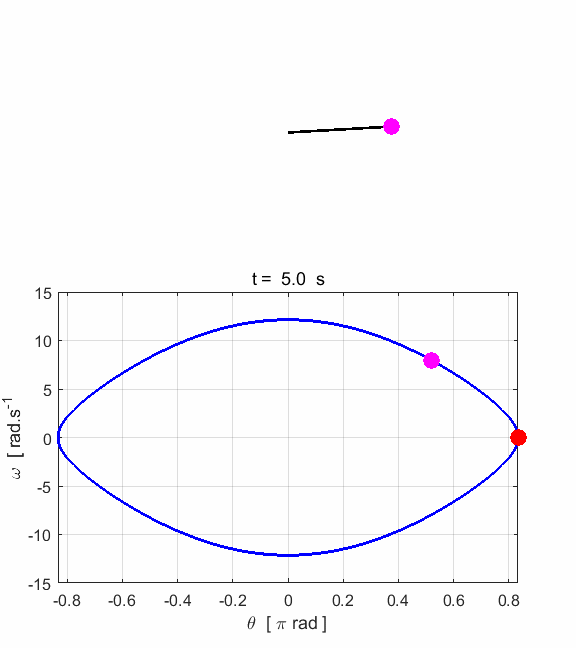
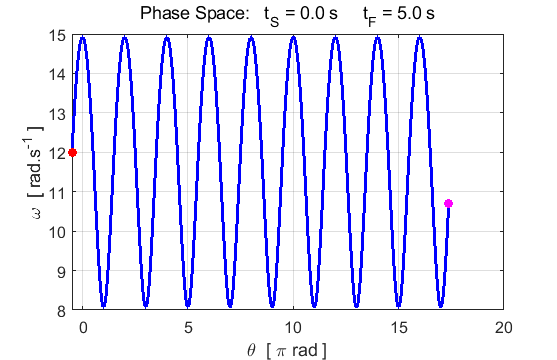
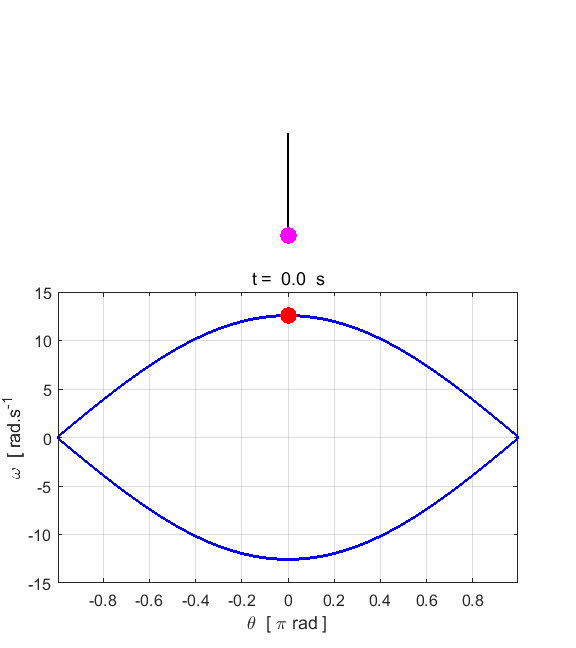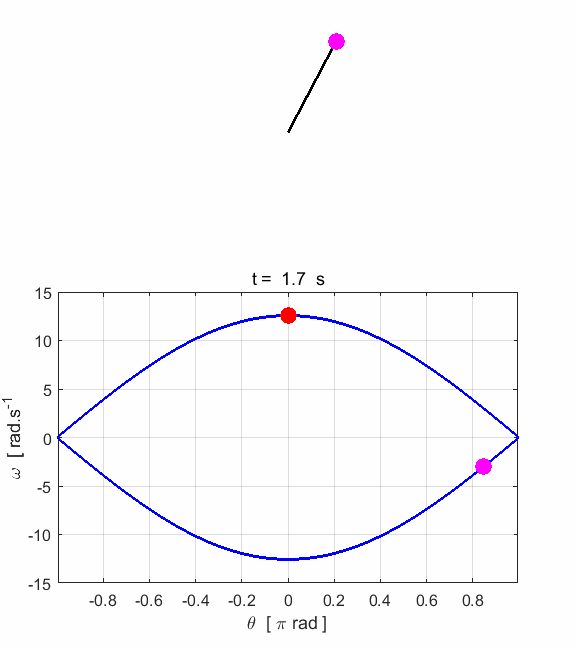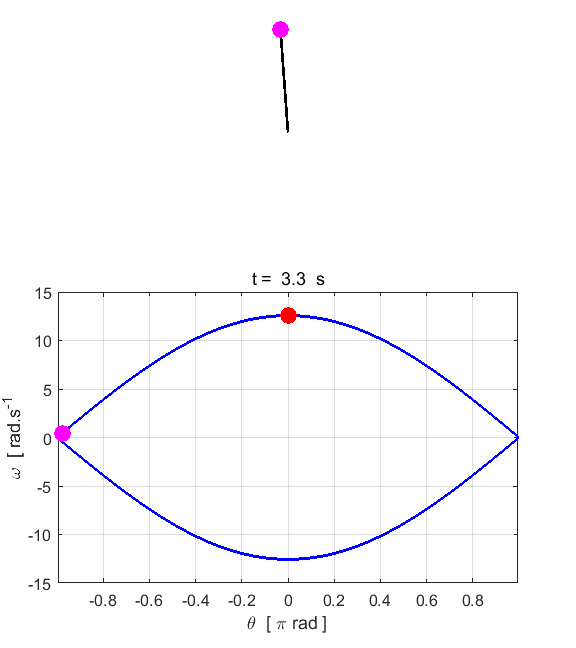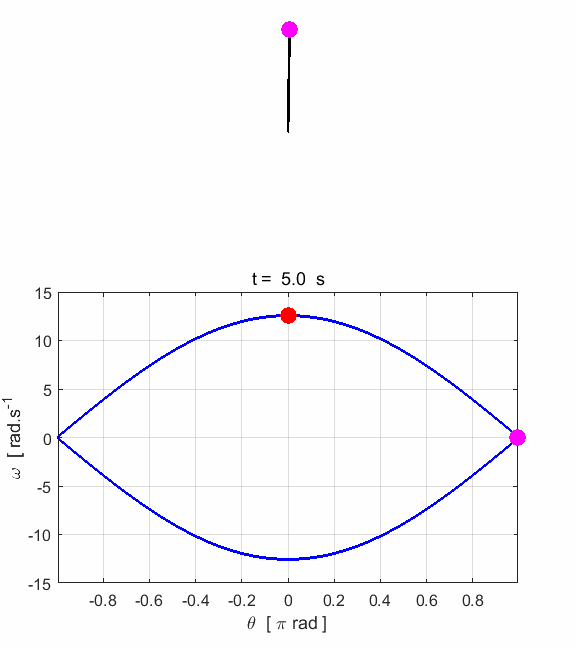
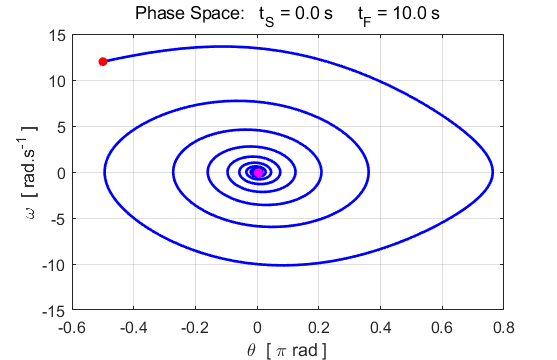
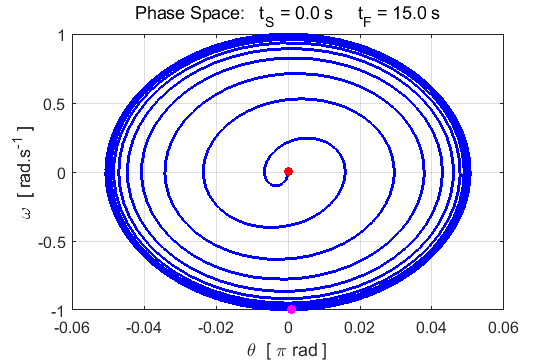
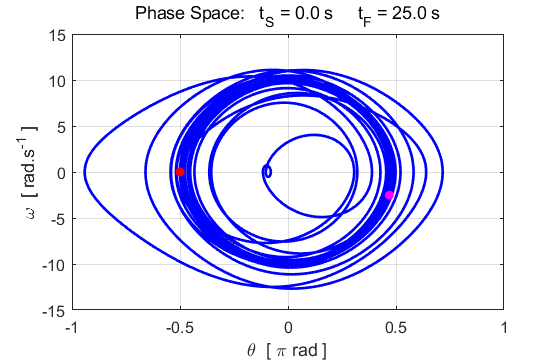
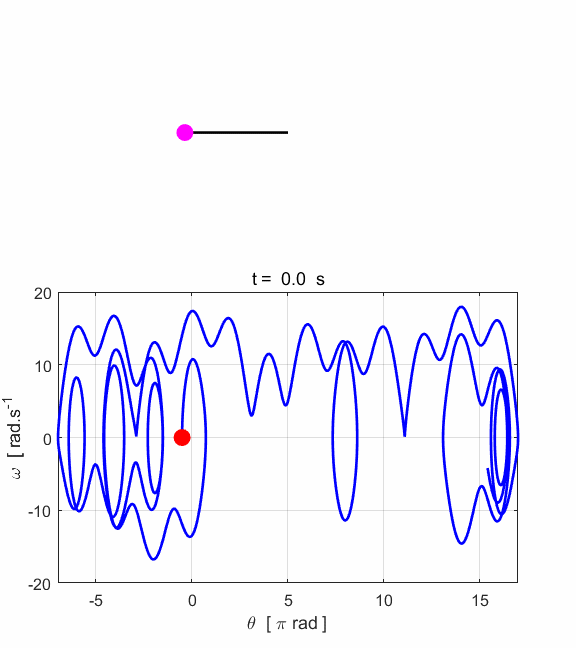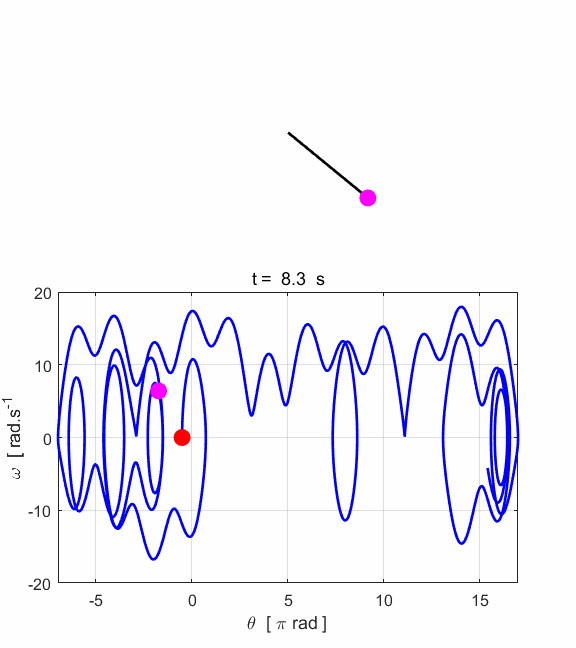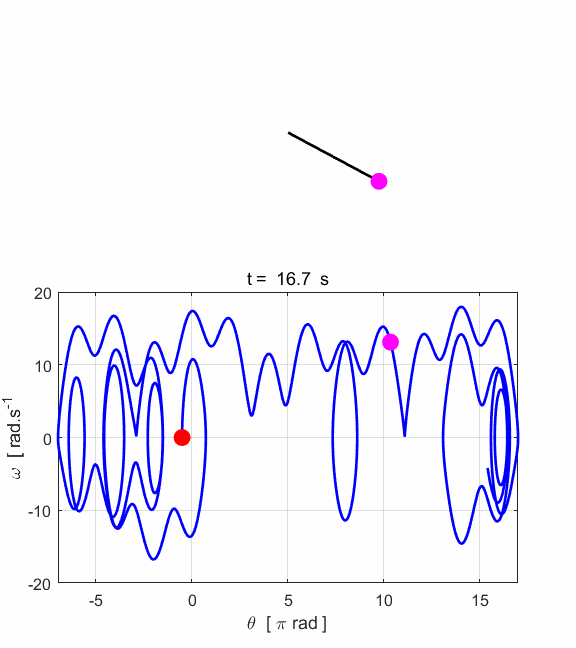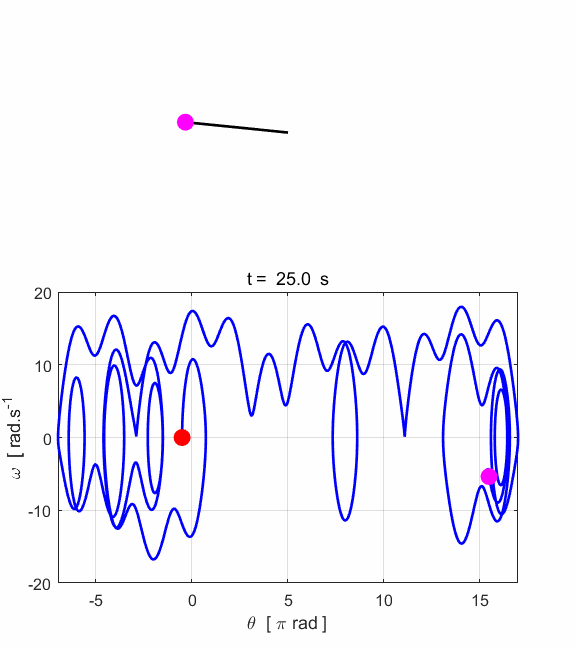
Fig. 1.2.  The phase space diagram for simple harmonic motion is an ellipse. The red dot shows the initial position of the pendulum bob and the magenta dot, the final position. After 5 periods, the pendulum does not return to its initial starting position. Therefore, the motion is not truly simple harmonic motion. If you make the initial angular displacement smaller, then the better the approximation to simple harmonic motion.

 

Fig. 1.3.   Animated motion of the pendulum and its phase space plot.

 

 

Simulation #2    Large amplitude, free motion of the rigid pendulum

For large amplitude oscillations, the motion of the pendulum bob is no longer executing simple harmonic motion. However, the motion is still periodic.

 

Input parameters

          nT = 801     tMax = 5     tS = 1     tF = t(end)

         c(2) = 0     c(3) = 0     c(4) = 0           zero damping and zero applied force

         x(1) = 5/6     v(1)  = 0                    initial angular displacement and angular velocity

 

Graphical outputs

Fig. 2.1.   Large amplitude oscillations. The pendulum is no longer executing simple harmonic motion. The motion however is still periodic. The period is now longer .

 

Fig. 2.2.  Phase space portrait for the motion of the pendulum. The trajectory forms a closed loop which is called the limit cycle. The closed loop indicates that the motion of the pendulum is periodic.

     Fig. 2.3.   Animated motion of the pendulum in phase space.

 

 

 

Simulation #3     Free rotation of the pendulum

The pendulum is given an initial push so that is continually rotates in an anticlockwise sense

 

Input parameters

          nT = 801     tMax = 5     tS = 0     tF = t(end)

          c(2) = 0     c(3) = 0     c(4) = 0           zero damping and zero applied force

          x(1) = -/2     v(1)  = 12                  initial angular displacement and angular velocity

 

Graphical outputs

     Fig. 3.1.   The pendulum spins in anticlockwise sense.

 

     Fig. 3.2.   Phase space portrait. 

Fig. 3.3.   Animated motion of the spinning pendulum. There is no orbit for the phase plot – the phase space curve is an open one. 

 

 

Simulation #4     Unstable equilibrium

The pendulum starts at the bottom of its swing in the stable equilibrium fixed point. The pendulum is given an initial velocity so that the pendulum will swing to a point vertically above the pivot point. This point is an unstable fixed equilibrium point. The pendulum hovers at the unstable equilibrium fixed point momentarily before falling. How big a push do we need? The initial velocity can be estimated from the principle of conservation of energy

     Initial total energy at the bottom of the swing  

               

     Final total energy at the bottom of the swing  

                     

  Energy is conserved      

  Initial angular velocity  

            

 

Input parameters

          nT = 801     tMax = 5     tS = 0     tF = t(end)

          c(2) = 0     c(3) = 0     c(4) = 0           zero damping and zero applied force

          x(1) = 0     v(1)  = 12.566                 initial angular displacement and angular velocity

 

Graphical outputs

Fig. 4.1.  The pendulum comes to rest momentarily at the unstable equilibrium fixed point directly above the pivot before falling.

 

     Fig. 4.2.  Phase space plot is a closed loop (limit cycle) indicating a periodic orbit.

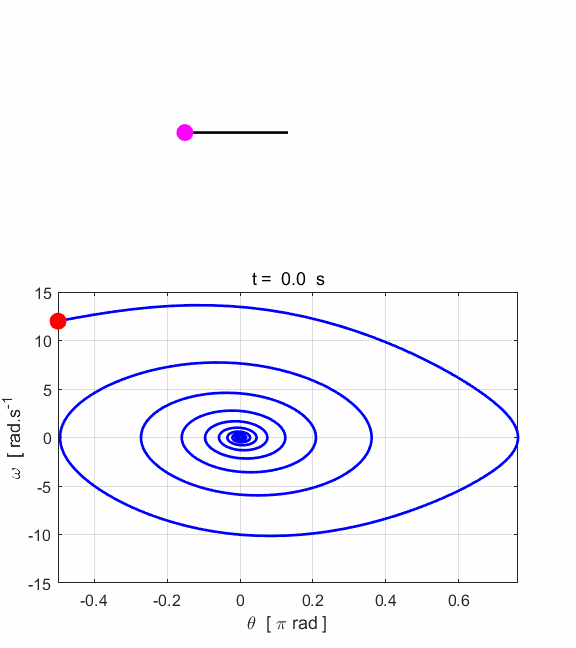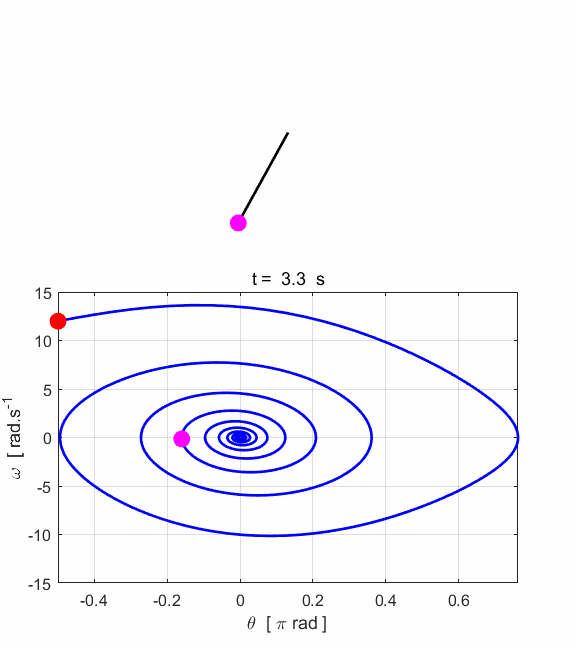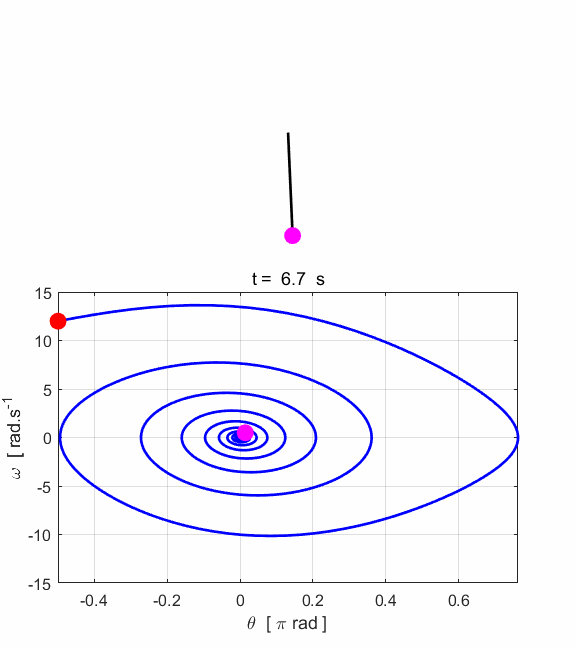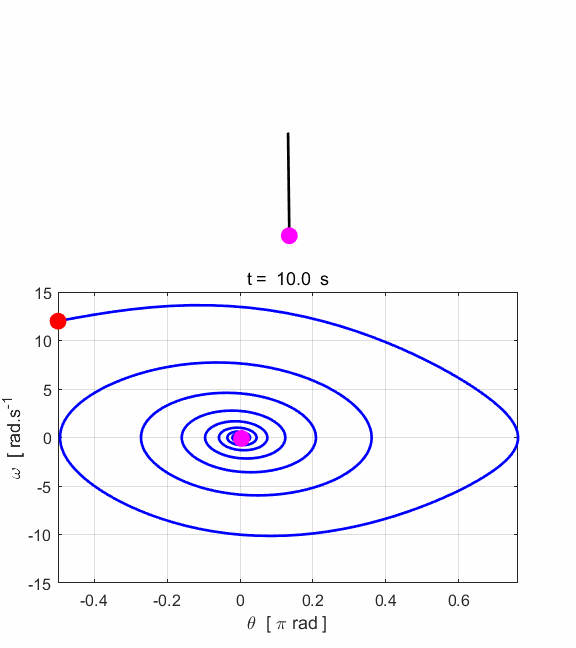
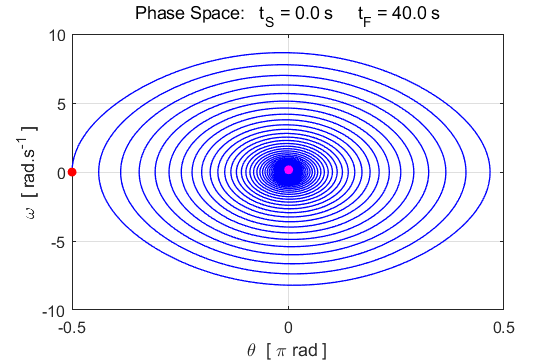
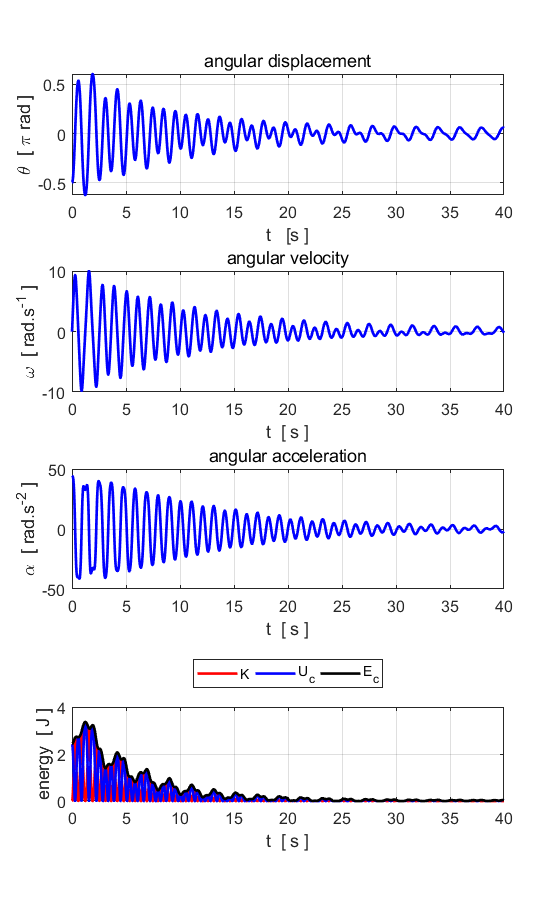
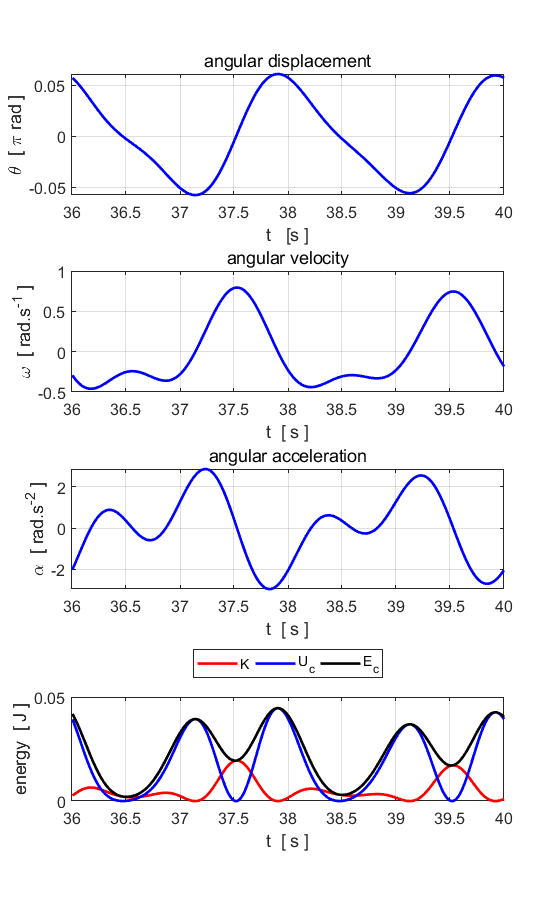
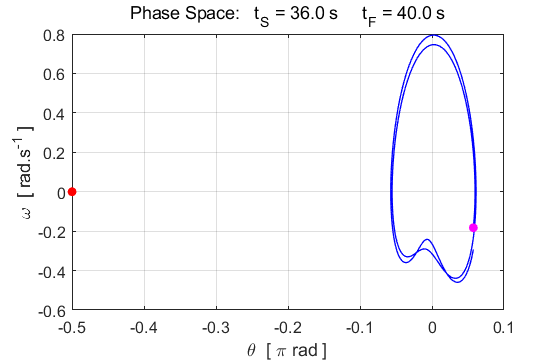
     Fig. 4.3.  Animation of the phase space plot.

 

 

Simulation #5     Damped motion

The phase space plot is a very important one to help you visualize the behaviour of our system and to understand chaotic dynamics. The viscous damping causes the pendulum to slow down as energy is dissipated and lost to the surroundings.  The behaviour of the pendulum slowing down, and the motion attracted to a fixed equilibrium point is illustrated very well in a phase space plot. The simulations for damped motion have the same initial conditions use in Simulation #3 (free rotation). Increasing the magnitude of the variable c(2) increasing the damping of the system. Try different simulations by increasing the value of c(2). Before running a simulation, predict the behaviour of the system and then test your predictions

 

Input parameters

          nT = 801     tMax = 5     tS = 0     tF = t(end)

          c(2) = 1     c(3) = 0     c(4) = 0           zero applied force

          x(1) =      v(1)  = 12                initial angular displacement and angular velocity

 

Graphical outputs

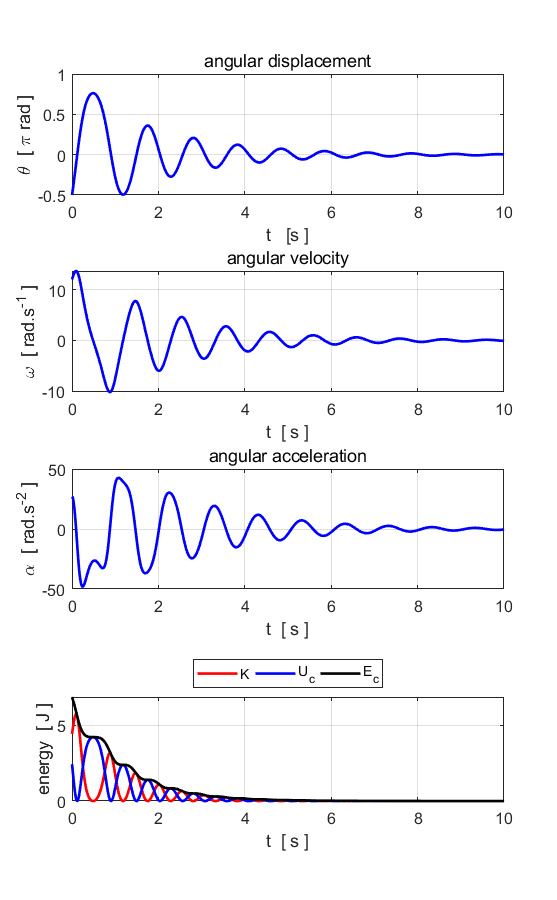
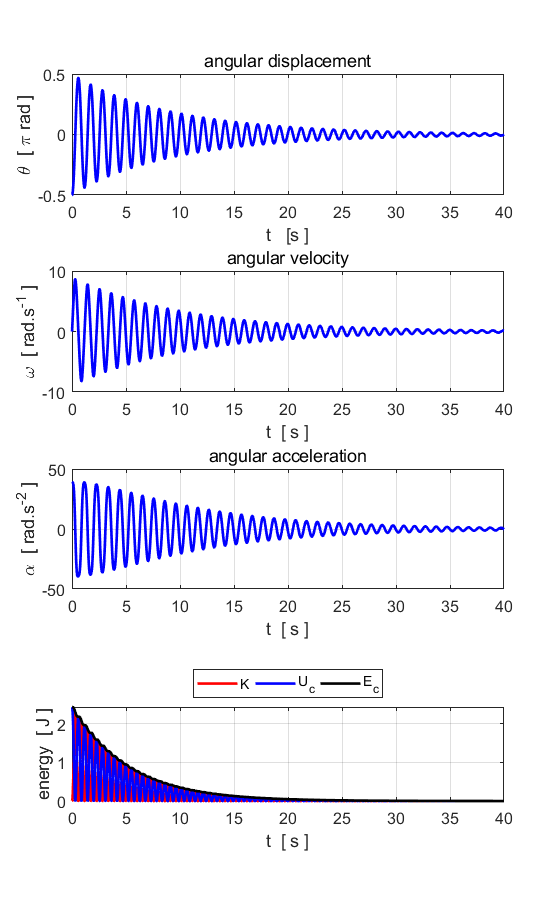
Fig. 5.1.  The motion of a damped pendulum. Energy is dissipated and lost to the surroundings.

 

In the above plots, the pendulum swings with a decreasing amplitude until is stops at the fixed point  . This point is called an attractor. An attractor is a set of points in phase space towards which a dynamical system evolves with time t. The attractor is a fixed point for our rigid damped pendulum. For an undamped oscillating pendulum, the attractor is an ellipse. This curve is called a limit cycle – a closed curve in phase space towards which an orbit may evolve as . For the damped pendulum, the attractor is the set of points  . See figure 5.3.

Fig. 5.2.   Animated motion of the damped pendulum.

 

Input parameters   increased damping

          nT = 801     tMax = 5     tS = 0     tF = t(end)

          c(2) = 2     c(3) = 0     c(4) = 0           zero applied force

          x(1) =      v(1)  = 20                initial angular displacement and angular velocity

 

Graphical outputs

 

 Fig. 5.3.   Strong damping causes the oscillations to quickly die-away. The attractor at the fixed point in phase space is .

    Fig. 5.4.   Animation of the damped motion of the pendulum.

 

 

Simulation #6     Forced damped motion:  RESONANCE

One can study the phenomenon of resonance when a damping force and external driving force act upon the system. The damping force causes the dissipation of energy from the system. However, an externally applied force may add or subtract energy from the system. When the frequency of the driving force is equal to the natural frequency of oscillation of the pendulum, then, maximum energy can be transferred into the system by the externally applied driving force. This results in the maximum amplitude of oscillation of the pendulum (provided that the strength of the driving force is not too large). If the driving frequency is not equal to the natural frequency, then the system will oscillate at the frequency of the driving force with a lower amplitude as a smaller net amount of energy is transferred to the system. The greater the difference in the frequency of the driving force and the natural frequency, then, the smaller the amplitude of pendulum oscillation.

 

Input parameters    RESONANCE

          nT = 801     tMax = 15     tS = 0     tF = t(end)

          c(2) = 1     c(3) = 1     c(4) = 2*pi/T0     driving frequency = natural frequency         

          x(1) = 0     v(1)  = 0                                   initial angular displacement and angular velocity

 

Graphical outputs

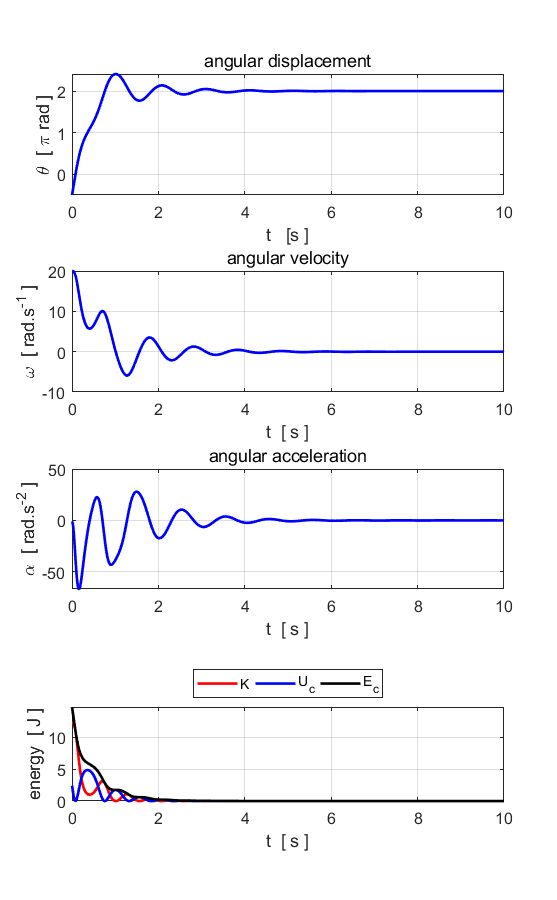
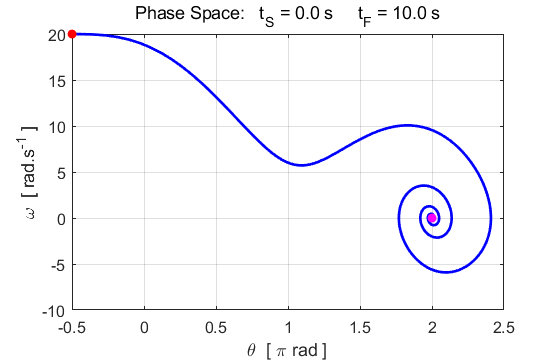
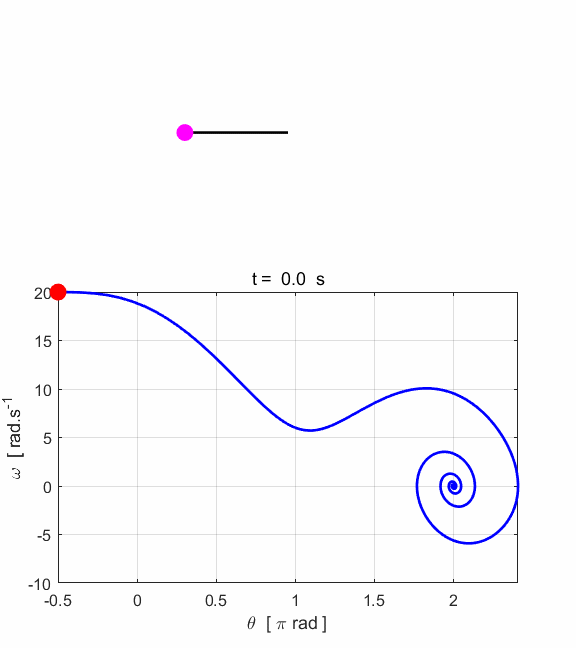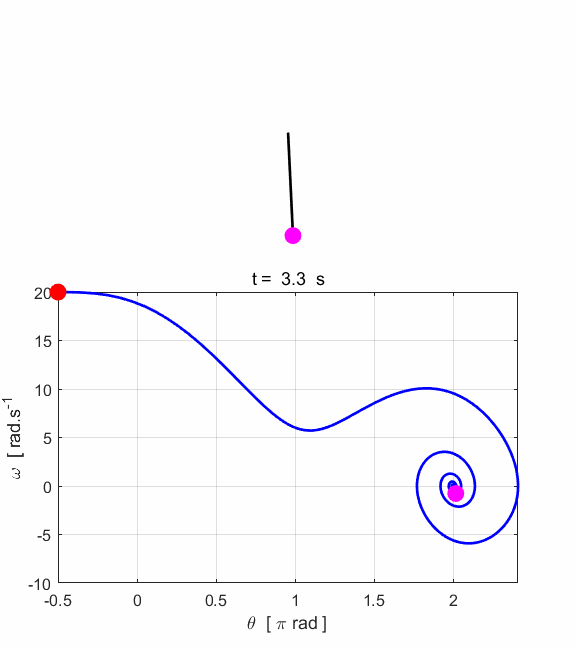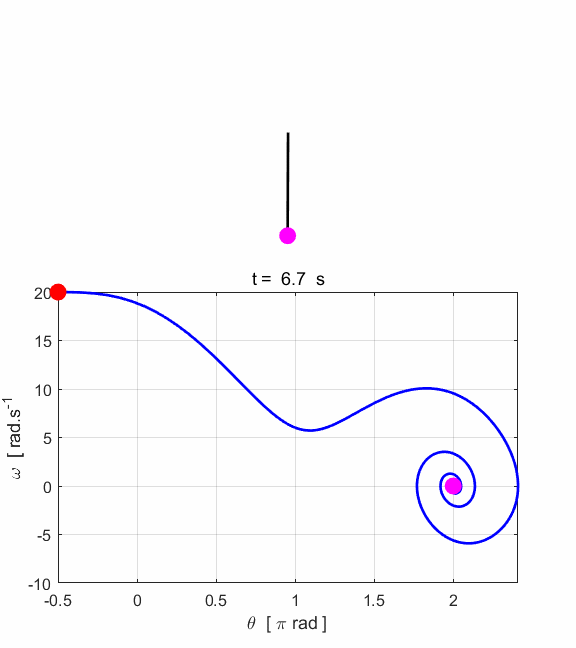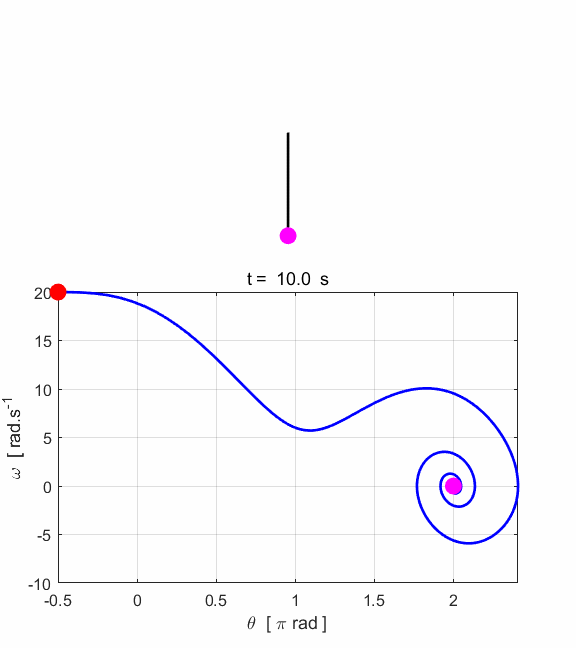
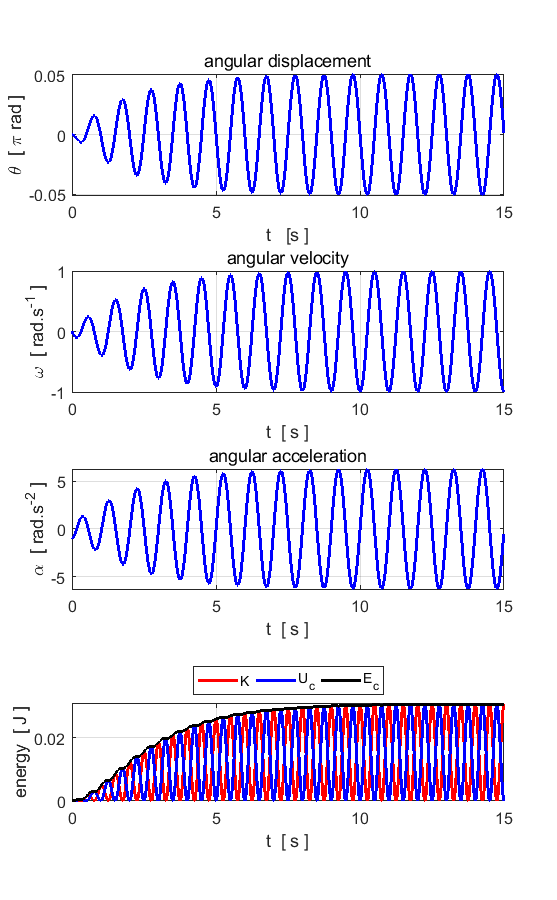
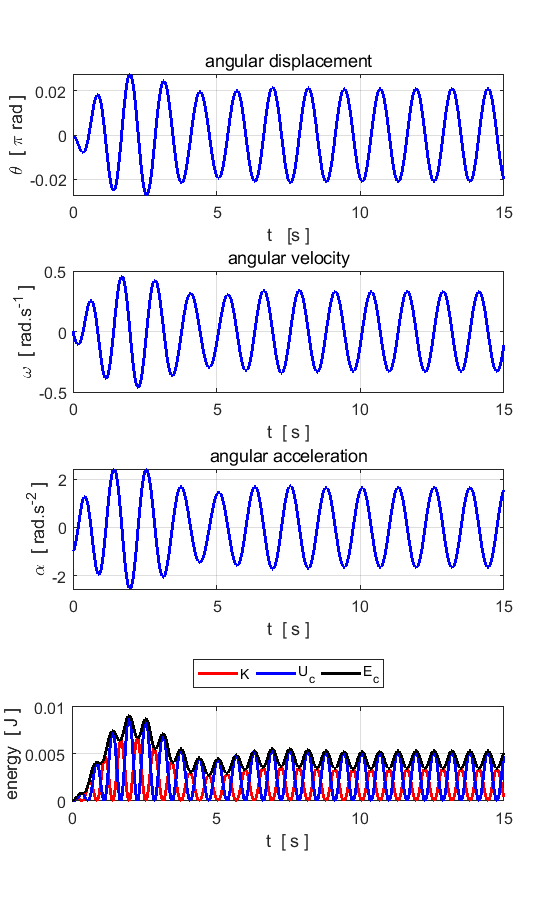
Fig. 6.1.   The applied external driving force transfers energy to the pendulum while energy is lost from the system because of the viscous damping force. After approximately 8 s the energy dissipated and transferred to the system balance and then the total energy remains constant and the pendulum swings back and forth in a periodic manner with a period of 1.0 s (period of driving force = natural period of oscillation).

 

 

 

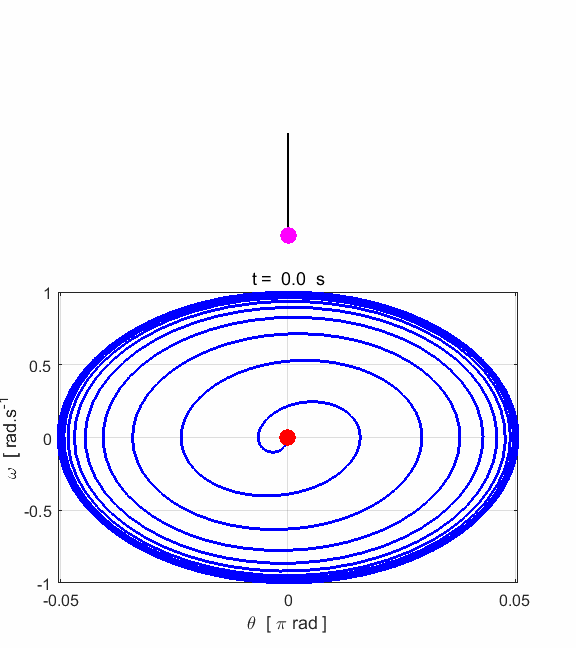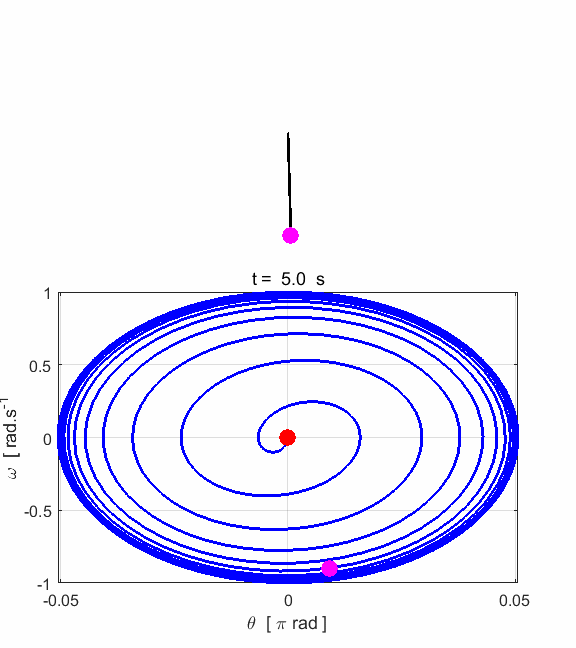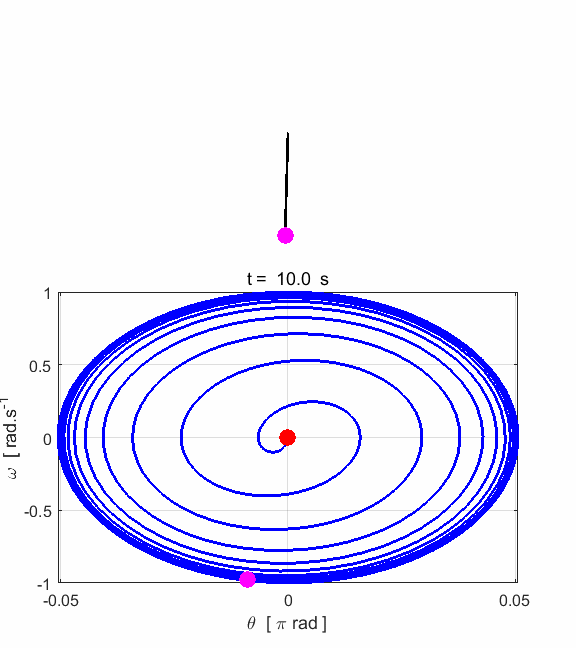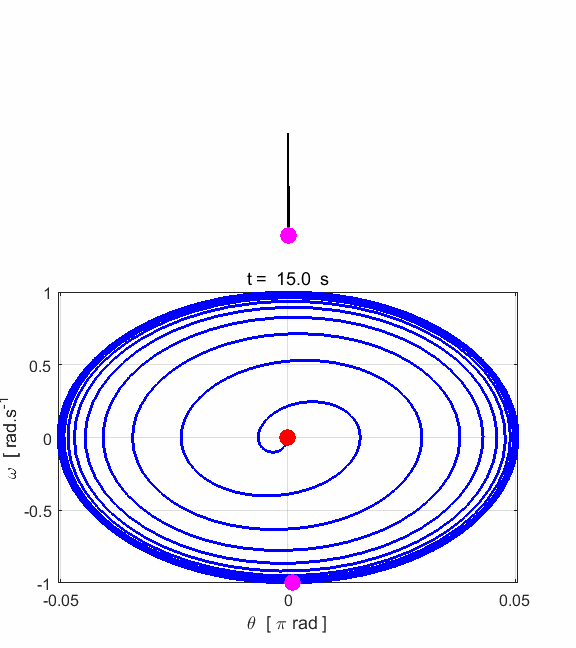
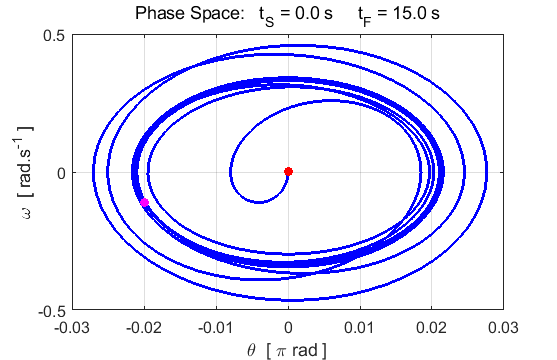
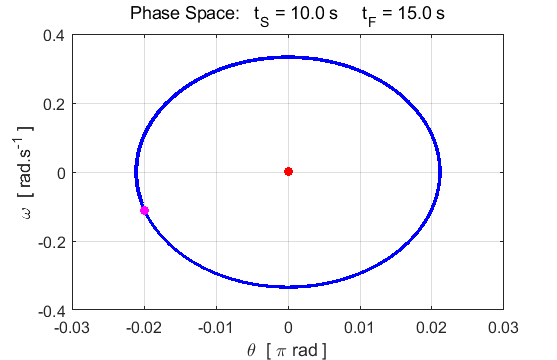
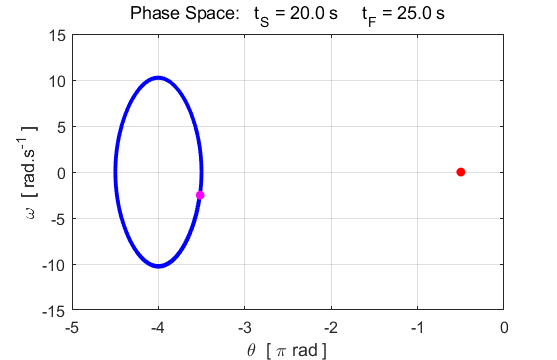
Fig. 6.2   The amplitude of the oscillation increases until the amplitude reaches its maximum value. After about 8 s a steady elliptical orbit is achieved in the phase space plot (nS = 8).

     Fig. 6.3.  Animation of the oscillating pendulum.

 

Input parameters    System not excited at its natural frequency

          nT = 801     tMax = 15     tS = 0     tF = t(end)

          c(2) = 1     c(3) = 1     c(4) = 0.8*2*pi/T0     driving frequency < natural frequency         

          x(1) = 0     v(1)  = 0                                           initial angular displacement and angular velocity

 

Graphical outputs

Fig. 6.4.   The driving frequency is less than natural frequency. The pendulum swings with a smaller amplitude as less energy is added to the system.

 

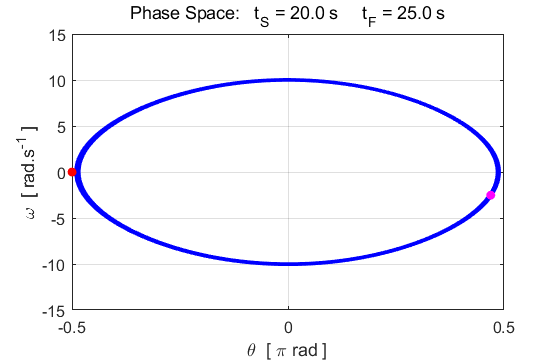
Fig. 6.5.   The phase space plot is a very useful way to illustrating important aspects of the motion. After some transient behaviour (~ 8 s), the system stabilizes. The trajectory encircles the point  and the orbit becomes periodic.  In phase space, the trajectory evolves towards a closed orbit called a limit cycle. The lower plot shows the limit cycle more clearly as the plots shows the trajectory only after some time has evolved from the initial conditions (nS = 10).

 

     Fig. 6.6.  Animation of the pendulum motion.

 

 

Simulation #7     The road to chaos

Adding a driving force increases the complexity of the phase space plots. Small changes in the strength of the driving force may result in very different trajectories of the pendulum. It is not possible for the motion of the pendulum to be chaotic if the forces acting of the pendulum are only the gravitational force and the damping force. Chaos can only occur if an external driving force also acts on the system and the driving frequency is less than the natural frequency of oscillation . If  and as the driving force increases from zero to larger values, you may observe the phenomenon of period doubling. A period doubling bifurcation in a discrete dynamical system is a bifurcation in which a slight change in a parameter value in the system's equations leads to the system switching to a new behaviour with twice the period of the original system. With the doubled period, it takes twice as many iterations as before for the numerical values visited by the system to repeat themselves. A period doubling cascade is a sequence of doublings and further doublings of the repeating period, as the parameter is adjusted further and further. Period doubling bifurcations occur in continuous dynamical systems, namely when a new limit cycle emerges from an existing limit cycle, and the period of the new limit cycle is twice that of the old one. However, it is difficult to find a set of values for the c coefficients and initial conditions that demonstrate the phenomenon of period doubling.

When the strength of the driving force exceeds a critical value, the motion becomes chaotic -the motion of the pendulum becomes erratic and unpredictable since very small changes in any parameters such as time step, initial values results in a very different trajectories.

 

Model parameters

Default values:    m = 1.0000 kg   g = 9.8000 m.s-2    T0 = 1.0000 s   à  

                               w0 = 2*pi rad.s-1 = 6.2832  rad.s-1   f0 = 1.000    L = 0.2482 m

                               c(1) = 4*pi^2 = 39.4784  rad2.s-2  

 

The damping given by coefficient c(2) should not give critical or overdamping, otherwise, the value used is not so important.


Input parameters:    driving frequency = natural frequency         

          nT = 10000     tMax = 25     tS = 0     tF = t(end)

          c(2) = 0.5     c(3) = 17     c(4) = 2*pi/T0       driving frequency = natural frequency         

          x(1) = -pi/2     v(1)  = 0                                   initial angular displacement and angular velocity

 

Graphical outputs

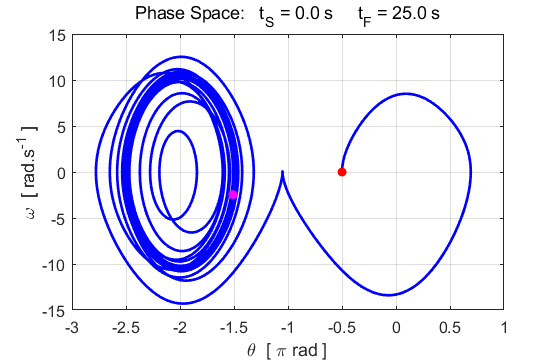
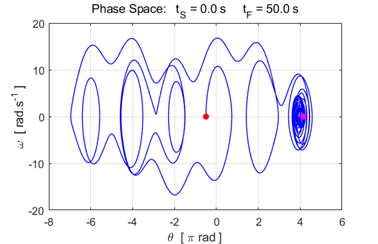
Fig. 7.1.   For values of the strength of the external driving force c(3) up to about 17, the angular displacement to a good approximation is given by a sine curve and the phase space plot is an ellipse (closed loop: limit cycle) with its centre at the fixed point attractor   indicating periodic motion with a period of 1.0 s. The pendulum oscillates at the driving frequency which is also equal to the natural frequency of oscillation. Small changes in the initial conditions or time step has negligible impact upon the motion of the pendulum.

 

The strength of the driving force c(3) increased slightly: 17 à 18.

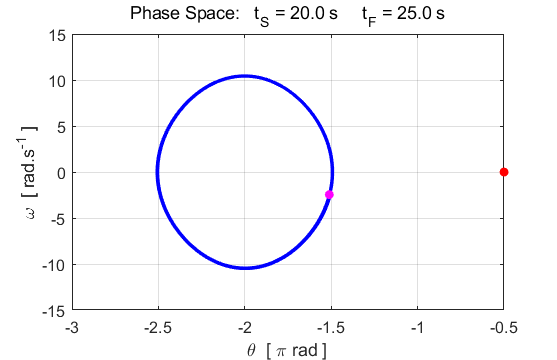
The increase in the driving force causes the trajectory to wander in a haphazard manner that appears to be chaotic but is not. The trajectory moves away from the fixed-point attractor at  to the attractors  and   until the trajectory becomes stable and periodic again around the fixed point attractor. The period of motion of the pendulum is still 1.0 s.

 

Fig. 7.2.   The motion of the pendulum for driving force strength c(3) = 18. The motion becomes periodic around the fixed-point attractor .

 

 

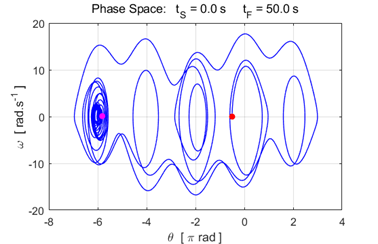
Fig. 7.3.   c(3) = 19. The pendulum motion stabilizers about the fix-point attractor .

 

 

Input parameters:  Driving frequency < natural frequency 

            Increasing the strength of the driving forces --> chaos       

                       nT = 10000     tMax = 40     tS = 0     tF = t(end)

                       c(2) = 0.2     c(3) = 0     c(4) = 0.5*w0       driving frequency < natural frequency         

                       x(1) = -pi/2     v(1)  = 0                initial angular displacement and angular velocity

 

Graphical outputs

 

 

Fig. 7.5.   c(3) = 0   Damped system with zero driving force.  The oscillations die-away and the pendulum comes to rest at the fixed-point attractor .

 

 

c(3) = 5

 

 

Fig. 7.5.   c(3) = 5   The period of the oscillation is now 2.0 s, which is double the period of the driving frequency TExt = 1.0 s. The doubling of the period is shown clearly by the double orbit in the zoom phase space view (lowest plot).

 

 

c(3) = 7

 

Fig. 7.6.   c(3) = 7   Periodic motion with a 2.0 s orbit around the fix-point attractor at .

 

c(3) = 15

 

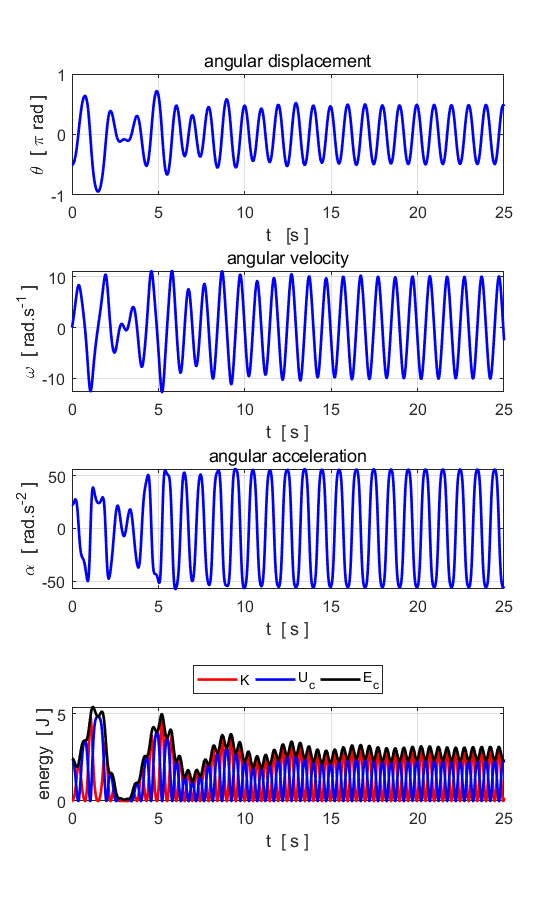
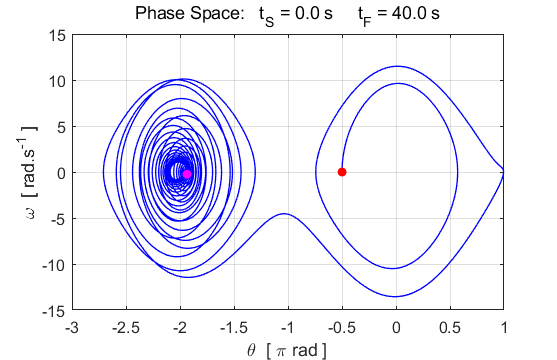
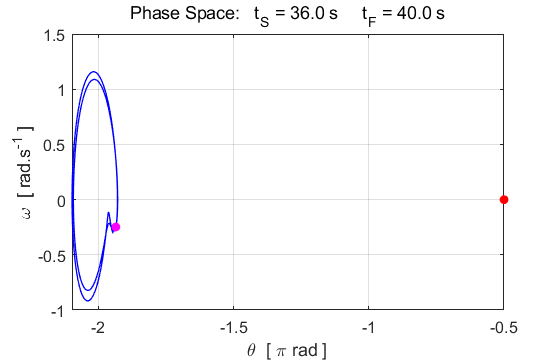
     Fig. 7.7.   c(3) = 15   The motion of the pendulum is now chaotic.

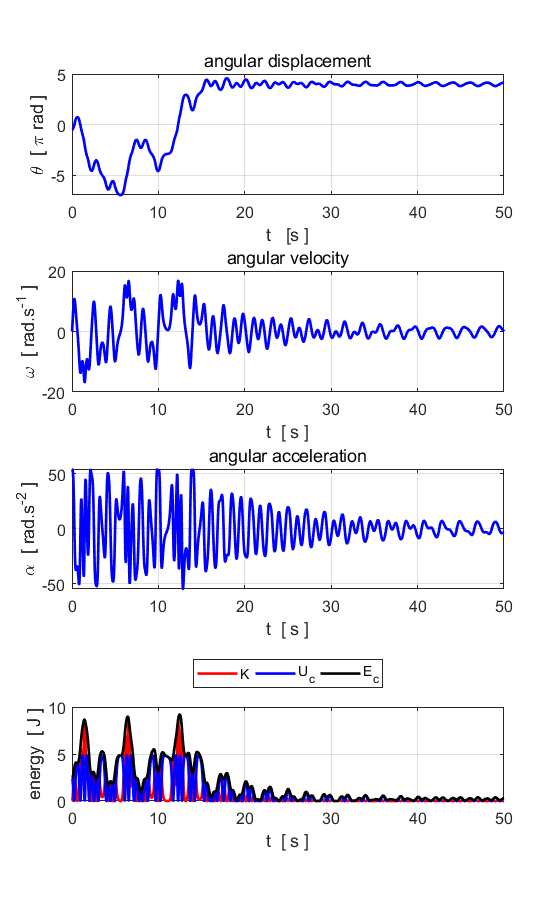
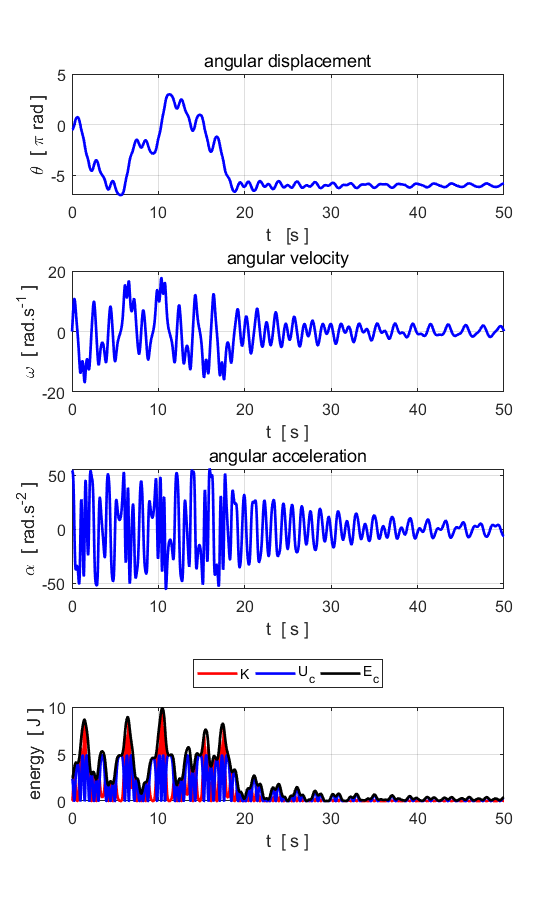
Fig. 7.7.   c(3) = 15   v(1) = 0.001    The motion of the pendulum is now chaotic. The slight increase in the initial angular velocity (0.000 à 0.001) produces a very different oscillation pattern.

 

Fig. 7.7.   c(3) = 15   The chaotic motion of the pendulum is now chaotic. The motion is not predictable since a slight change in initial values gives a very different trajectory.

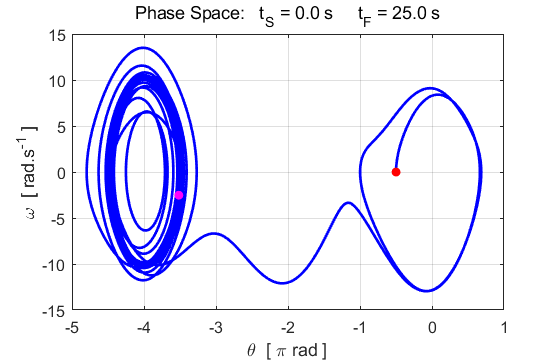
Left plot:  v(1) = 0.000 and right plot: v(1) = 0.001. The motion is truly chaotic.

 

 

When the motion of the pendulum has become chaotic, the trajectory in phase space wanders about aimlessly, sometimes the pendulum rotates clockwise and at other times it rotates anticlockwise about the pivot point. It appears to be pulled towards one of the stable points, then wanders away again to another attractor fixed point.

 

Fig. 7.8.   Animated motion of the chaotic pendulum for figure 7.6.

  

 

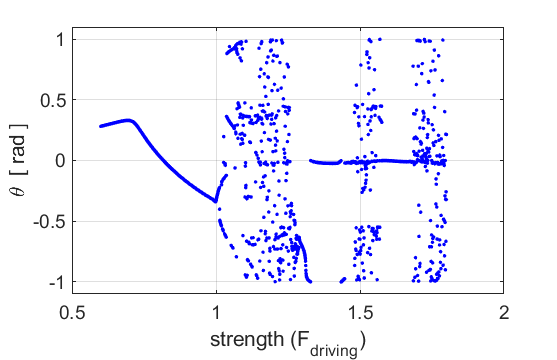
Simulation #8    BIFURCATION DIAGRAM

A bifurcation diagram can be used to show chaos. The script chaos07AB.m was used to give the bifurcation diagram shown in figure 8. The parameters used for the bifurcation are from Classical Mechanics by J. R. Taylor

 

 

Fig. 8.1.   Bifurcation diagram of a driven damped pendulum.  chaos07AB.m

The diagram may not be too good. Maybe there is a better way to get the bifurcation diagram.

 

Input parameters and Calculations:

% INPUTS ===========================================================

 

% Time domain

   nT = 5000;

% Max time interval

   tMax = 50;

            tMin = 0;

            t = linspace(tMin,tMax,nT);

            h = t(2) - t(1);

% Time interval for phase space plot start tS and finsih tF            

% Iindices nS and nF for plotting figure 3  phase space plot 

   tS = 0;

   tF = t(end);

           nS = find(t >= tS,1); nF = find(t >= tF,1); nR = nS:nF;      

% nautral frequency

   c(1) = 9*pi^2;         

% Damping constant  

   c(2) =  3*pi/2;

% Angular frequecny of driving force

   c(4) = 2*pi;

% Initial position of pendulum  xA [rad]  vA [rad/s]

             x = zeros(nT,1);

             v = zeros(nT,1);

   x(1) = 0;

   v(1) = 0.000;

 

% Strength of driving force c(3) = Fs*c1

% nS       number of calculations for varying strength of driving force

% Fs      strength of driving force factor

% theta   angular displacent at the end of the simulation

%         -pi <= theta <= +pi

   nS = 2000;

   Fs = linspace(0.6,1.8,nS);

   theta = zeros(nS,1);

 

% CALCULATIONS ========================================================

 

for cs = 1 : nS

    c(3) = Fs(cs)*c(1);

% Runga-Kutta Solution of differential equation

   for cc = 1 : nT-1

       [k1, k2, k3, k4] = coeff(t(cc),h,x(cc),v(cc));

 

       x(cc+1) = x(cc) + h*(v(cc) + (k1 + k2 +k3)/6); 

     

       v(cc+1) = v(cc) + (k1 + 2*k2 + 2*k3 + k4)/6;

   end

  

   theta(cs) = x(end);

   while theta(cs) > +pi; theta(cs) = theta(cs) - pi; end

   while theta(cs) < -pi; theta(cs) = theta(cs) + pi; end

end