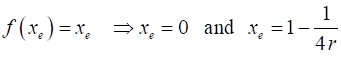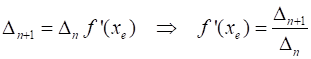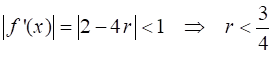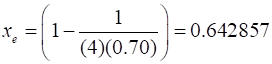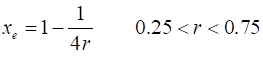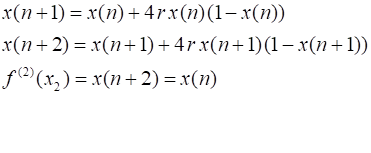DOING PHYSICS WITH MATLAB

 

Ian Cooper

matlabvisualphysics@gmail.com

 

DYNAMICAL NON-LINEAR SYSTEMS

LOGISTIC DIFFERENCE EQUATION

 

DOWNLOAD DIRECTORIES FOR MATLAB SCRIPTS

       Google drive

 

       GitHub

 

chaosLogisticsEq01.m

The logistic difference equation for the population  is iterated for a set of growth parameters r. The output gives an animated plot of the iterated values of the population  for increasing values of r. Another plot is the bifurcation diagram – a plot of the iterated values of  as a function of the growth parameter r.

 

chaosLogisticsEq02.m

The logistic difference equation for the population  is iterated for the specified initial population  and growth parameters r. The output gives a plot of the iterated values  and a plot of the quadratic function .

 

chaosLogiscticsEq03.m

Period doubling: plots of a [1D] mapping function f(n)(x) against the population x and the plot f(x) = x. The intersections of the two curves gives the fixed points. For a fixed point to be stable requires . A plot of the functions df/dx is superimposed upon the other two plots to find which fixed points are stable.

 

chaosLogisticsEq04.m

Finding the fixed points for the population dynamics from a [1D] mapping function for different orders.

 

 

INTRODUCTION

Biologists studying the variability in populations of various species where generations do not overlap found a simple difference equation that predicted the population trajectories reasonably well. One such equation is a simple quadratic equation called the logistic difference equation. Very surprising, this simple difference equation predicts under certain circumstances a fantastically complex and chaotic behaviour that was total unexpected.

 

The logistic difference equation is given by

 

            

            

 

where x(n) is a scaled population at iteration n and r is the control or growth parameter. The initial condition is specified by  where .  Each iteration can be considered as a single time step. The dynamics of this system is controlled by the single growth parameter r. The dynamical motion of the phenomenon is non-linear because of the quadratic term in the population .

 

                   This simple non-linear system does not possess simple dynamical properties

 

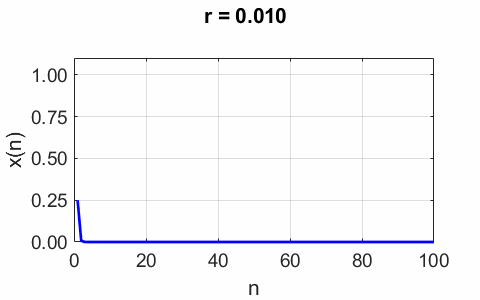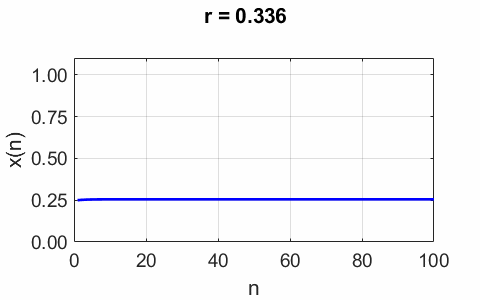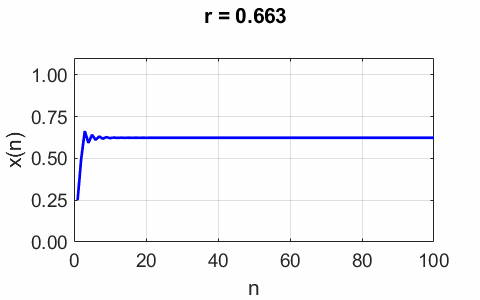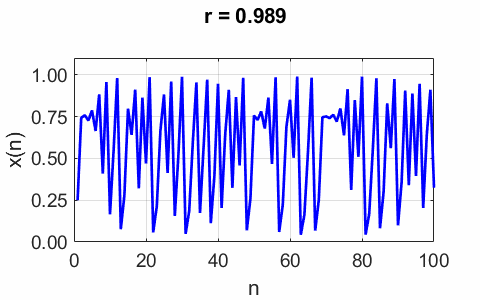
It is often observed in nature that a population x will increase from one generation to the next when small and decrease when large. This is expressed mathematically by the product  .

 

The population is computed for many time steps n = 1, 2, 3, . . .  , Nmax . Nmax = 100 to1000 is usually enough iterations so that the initial transient fluctuations in the population can be ignored and the population shows a steady state behaviour.

 

For small values of r, the population converges to a stable equilibrium population. As the value of r increases, interesting things happen as shown in figure 1.

 

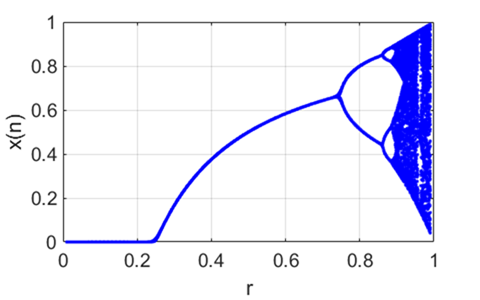
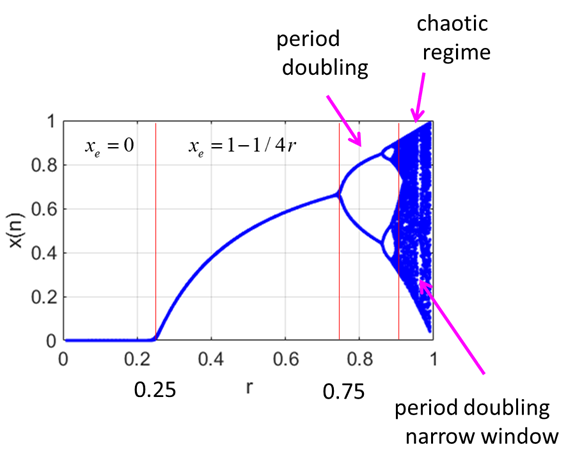
       Fig. 1.   Bifurcation diagram - plot of the iterated values of  as a function

   of the growth parameter r.  Note the transitions from stable equilibrium

   populations to oscillation and period doubling to chaotic behaviour and region

   of periodic behaviour within the region of chaos.    chaosLogisticsEq01.m

 

 

When r > ~0.75,  no longer converges to a single equilibrium population, but it oscillates between two values. This characteristic change in behaviour is called a bifurcation. Increasing the growth factor even further results in  oscillating between not two, but four values. This phenomenon is called period doubling.  As one continues to increase the growth parameter then  goes through bifurcations of period eight, then sixteen, . . . , then chaos! When growth parameter r > ~ 0.9, the population  neither converges or oscillates, but its value becomes completely random and the behaviour is largely chaotic. However, there is a particular value of r where the sequence again oscillates and period doubling occurs as r is slightly incremented.

 

Figure 2 show an animated plot of the iterated values of the population for increasing values of the growth parameter r. As r passes through one of its critical values, note the complete change in the dynamics of the system.

 

 

         Fig. 2.   Animated plot of the iterated values of the population  for

         increasing values of the growth parameter r.      chaosLogisticsEq01.m

 

The quadratic expression in the logistic difference equation is

             

 

The function  is called a one-dimensional map since the function  transforms any point on the [1D] interval , into some other point in the same interval. The plot shown in figure 2 can be referred to as the orbit of x for the [1D] map .

 

 

PERIOD 1 DYNAMICS         

 

The orbit of the population x is attracted to an equilibrium point or fixed point  for lower values of the growth parameter r where , therefore,

                            

One obvious fixed point is . The other fixed point is

           

 

We can derive analytical expressions for the fixed points of the [1D] map   to check the stability of the fixed points . The fixed-point condition is

          

 

Since , the only fixed point for  is  which means that the population will become extinct.

 

To determine the stability of the fixed points , we let

            

 

and we have

          

          

 

If  then the orbit will iterate away from since .

 

If  then the orbit will iterate towards since .

 

 

Thus, the local stability criteria for a fixed point are shown in figure 3.

       Fig 3.   Stability of fixed points

 

The first derivative is

              

Thus, for the equilibrium point  to be stable requires

            

 

Therefore, we can conclude

           

 

 

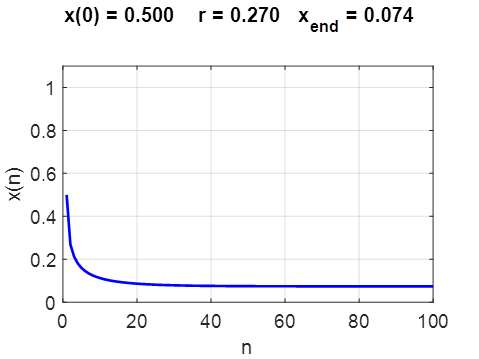
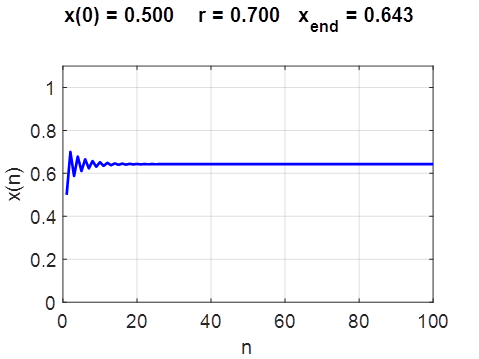
The local curvature of the curve  determines the change in x each time f  is iterated. At a fixed point, only when the local slope is less than one, does the next iterated population approaches a stable fixed point, otherwise, the next iterated value of the population diverges from the unstable fixed point. So, for  the dynamics of the orbit is completely known, the population will eventually converge to one of the two fixed points irrespective of the initial population .

 

Using the Script  chaosLogisticsEq02.m  you can explore the dynamical behaviour of the system by inputting different values for the initial population , the growth parameter r and the number of iterations N.  Figure 4 shows the orbit when  for a set of different initial populations. The stable fixed point is .

                Fig. 4.   Plots of the iterated population .  for different

                initial populations x0 = 0.01,   x0 = 0.50 and x0 = 0.95. The stable fixed

                point is  and its value is independent of the initial population.

                                   chaosLogisticsEq02.m

 

 

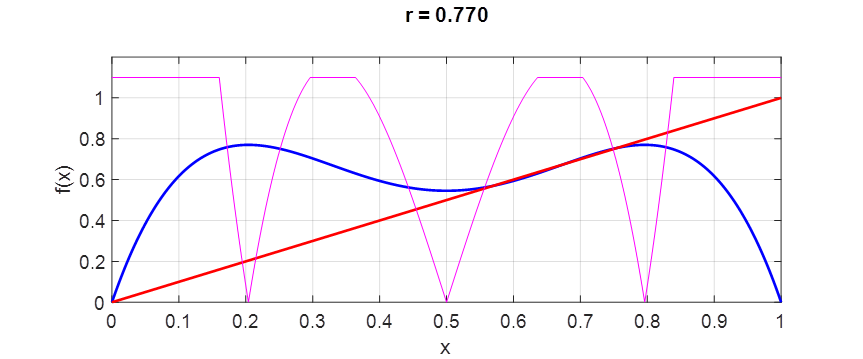
 This dynamic is said to be period 1. A simple graphical method is shown in figures 5 - 8 for finding the fixed points. The plot shows the graph of  and the straight line corresponding to y = x.  The intersection of the two curves gives the fixed points  and . For a growth parameter r, the upper graph shows the obit to the attractor xe. The lower graph, shows a plot of the iteration function  against the population x (blue- parabola), the straight line  f(x) = x (red – straight line) and the derivative of the function  (magenta). The curvature function  is capped at 1.1. A fixed point is given by the intersection of the curves  and . Only, if the slope of the [1D] map function  is less than one is the fixed point  stable .  You can see the critical values of r at the points where .

 

Fig. 5.   Iteration of the map  with . Since   the

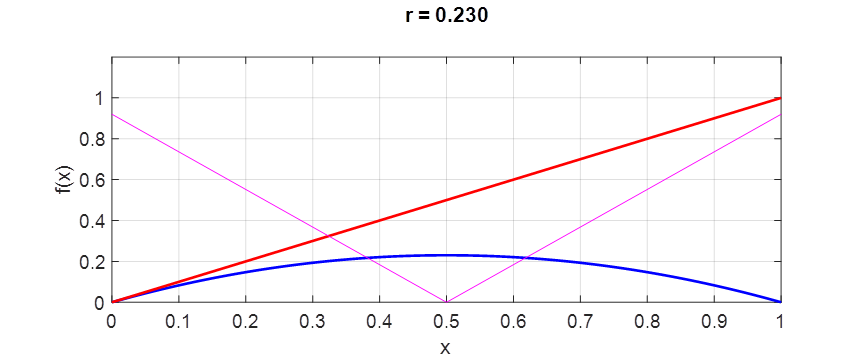
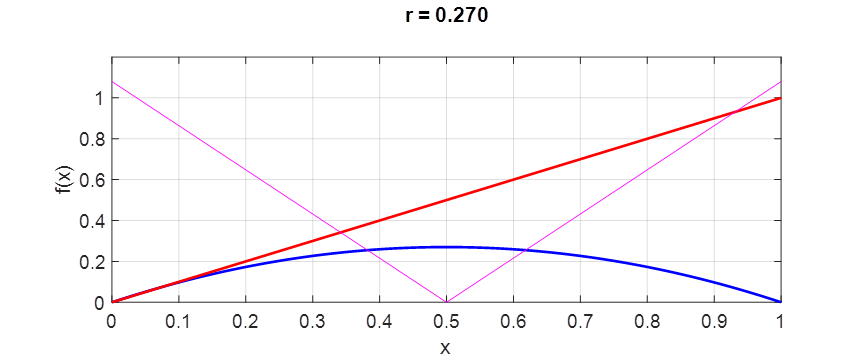
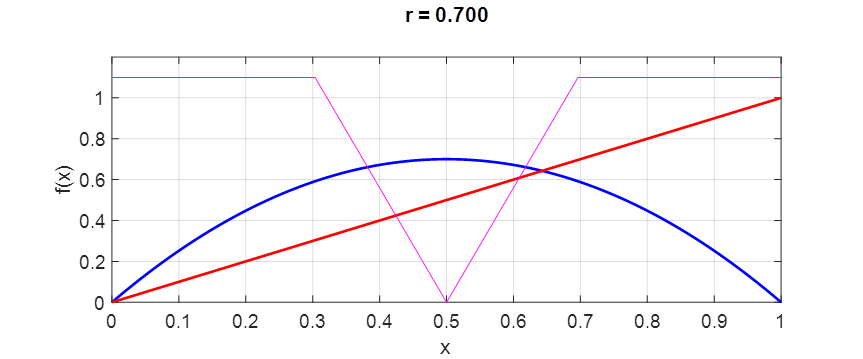
single stable fixed is   where .

               chaosLogisticsEq02.m      chaosLogisticsEq03.m

 

Whenever the growth parameter is less than 0.25 , the population will become extinct. 

 

 

Fig. 6.   Iteration of the map  with .

Since   there is a single stable fixed  where .

          The value of the intersection point agrees with the analytical value           

                          chaosLogisticsEq02.m      chaosLogisticsEq03.m

 

 

           Fig. 7.   Iteration of the [1D] map  with

           .  The intersection of the [1D] map and the

           line y = x gives the two fixed points,  (trivial – unstable)  and

           is stable since the slope . The last iterated

          population  is equal to the fixed point  .

         The value of the intersection point agrees with the analytical value           

                       chaosLogisticsEq02.m   chaosLogisticsEq03.m

 

 

When  there is no longer a single fixed point as shown in figure 8.

 

 

 

           Fig. 8.   Iteration of the [1D] map  with

           . The intersection point is  and

          is not a stable fixed point since

           chaosLogisticsEq02.m       chaosLogisticsEq03.m

 

        

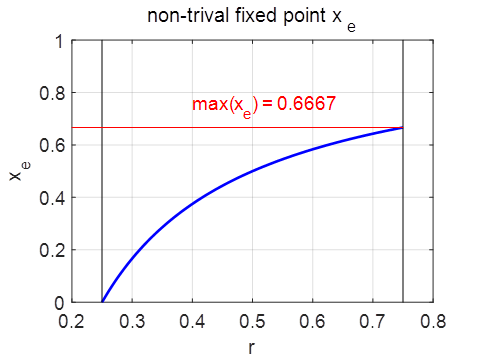
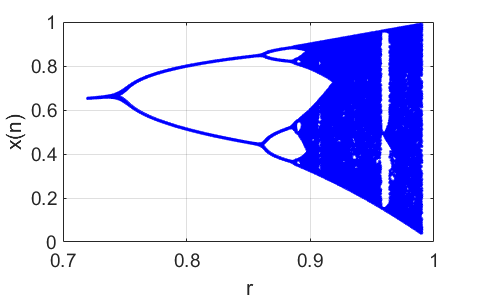
The maximum value for the stable fixed point is   when , as shown in figure 9.

 

            Fig. 9.   The period 1 stable equilibrium point  as a function of the growth parameter r

             

 

           All trajectories in the neighbourhood of a stable fixed will be attracted to it.

             chaosLogisticsEq03.m   

 

 

PERIOD DOUBLING DYNAMICS

The bifurcation diagram shown in figure 10 shows an expanded version of the figure 1 plot. It clearly shown the change in the dynamics in the evolution of the population when .

        Fig. 10.   Bifurcation diagram - plot of the iterated values of  as a function

   of the growth parameter r .  Note the transitions from stable equilibrium

   populations to oscillation and period doubling to chaotic behaviour and region

   of periodic behaviour within the region of chaos.    chaosLogisticsEq01.m

 

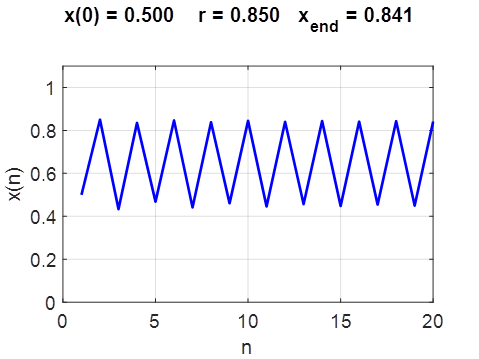
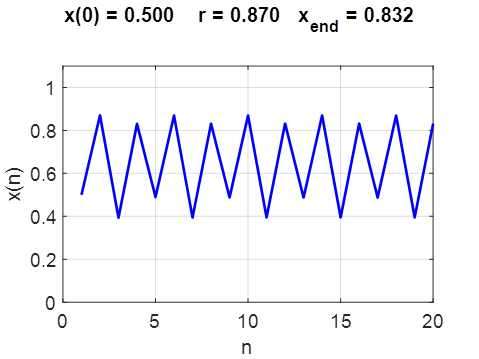
When , the fixed points of  f  become unstable and the orbit bifurcates to a cycle of period 2. Now, the population x returns to the same value only after every second iteration, that is

           

and there are now two attractors of f(x) with fixed points  and .

 

Fig. 11.   Period 2 dynamics .  The population x oscillates between the two fixed points . Hence the population x only returns to the same value after every second iteration . Note: at each fixed point .

chaosLogisticsEq02.m    chaosLogisticsEq03.m

 

Fig. 12.   Period 2 dynamics .  The population x oscillates between the two fixed points . Hence the population x only returns to the same value after every second iteration. Note: at each fixed point .

        chaosLogisticsEq02.m    chaosLogisticsEq03.m

 

 

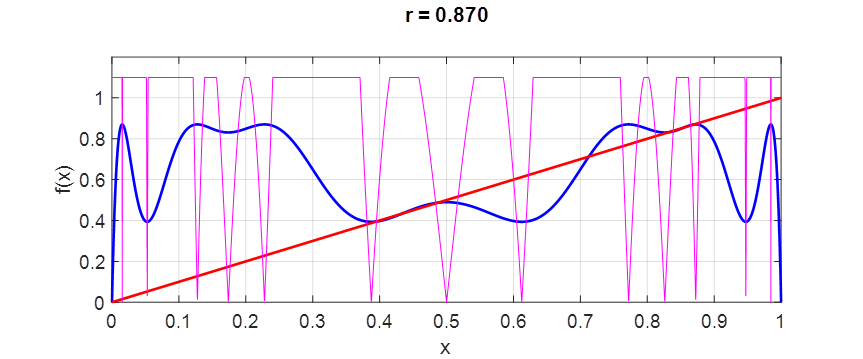
The period 2 dynamics is only exhibited in the range . If  another bifurcation occurs and the cycle of f  is period 4. The period 4 iteration is

           

Fig. 13.   Period 4 dynamics .  The population x oscillates between the four fixed points . Hence the population x only returns to the same value after every fourth iteration. Note: at each fixed point .               chaosLogisticsEq02.m    chaosLogisticsEq03.m

 

 

Increasing r again will lead to further bifurcations. This phenomenon is called period-doubling

        period 1 à period 2 à period 4 à period 8 à period 16 à  . . .

 

 

Fig. 14.   Period 8 dynamics .  The population x oscillates between the eight fixed points . Hence the population x only returns to the same value after every eight.  chaosLogisticsEq02.m   

 

 

Increasing r again , the changes in population x become chaotic where the evolution of the population never repeats itself and if the initial population is slightly changed it can give rise to very different orbits even after a small number of iterations.

 

Fig. 15.  Population orbits in the chaotic regime . After a small number of iterations, there are two very distinct orbits for the two initial values  (blue) and  (red).      chaosLogisticsEq02.m   

 

Fig. 16.  Bifurcation diagram. Plot of iterated values of x(n) as a function of the growth rate r.       chaosLogisticsEq01.m   

 

 

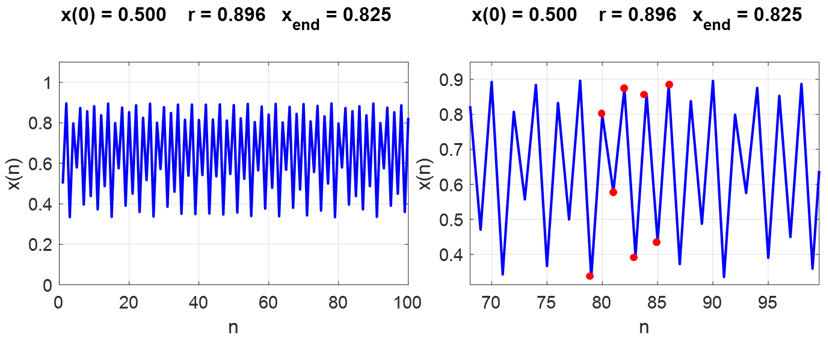
                Fig. 17.   Period 1 orbit in a narrow window within the region of chaos.

        chaosLogisticsEq02.m   

 

Figure 18 shows another animated view of the changing population dynamics for increasing values of the growth parameter r.

 

         Fig. 18.   The population orbit for increasing values of the growth parameter r.

         chaosLogisticsEq02.m   

 

Period doubling window

In the period doubling window, periodic motion again occurs where odd period dynamics may occur as shown in figures 19, 20 and 21.

          Fig.  20.  Bifurcation plot in period doubling window.    chaosLogisticsEq01.m   

 

         Fig. 21.   Period 3 dynamics                      chaosLogisticsEq02.m   

 

          Fig. 22.   Period 6 dynamics produced by the bifurcation of the period

          3 dynamics                     chaosLogisticsEq02.m   

 

 

PERIOD DOUBLING – FINDING THE FIXED POINTS OF THE DYNAMICS

The Script chaosLogisticsEq04.m can be used to find the fixed points and identify those points which are stable for any value of the growth parameter r. The input parameters for the Script are the growth factor r  and the period P . The population x is specified as a symbolic variable. The [1D] mapping functions are iterated and then solved to find the fixed points. The gradient of the mapping function is found to test the stability of each fixed point. The numerical results are displayed in the Command window.

 

A section of the Script chaosLogisticsEq04.m:

syms x

 

% Input growth factor r   >>>>>

  r = 0.960;

 

% Input dynamics period  P = 1, 2, 3, ... , 8 >>>>>

  P = 6;

 

 

% ITERATIONS =========================================================

% [1D] mapping functions

 f1 = 4*r*x*(1-x);

 f2 = 4*r*f1*(1-f1);

 f3 = 4*r*f2*(1-f2);

 f4 = 4*r*f3*(1-f3);

 f5 = 4*r*f4*(1-f4);

 f6 = 4*r*f5*(1-f5);

 f7 = 4*r*f6*(1-f6);

 f8 = 4*r*f7*(1-f7);

 

 if P == 1; f = f1; end

 if P == 2; f = f2; end

 if P == 3; f = f3; end

 if P == 4; f = f4; end

 if P == 5; f = f5; end

 if P == 6; f = f6; end

 if P == 7; f = f7; end

 if P == 8; f = f8; end

 

% Solve f(xe) = xe

  eq1 = f - x;

% Fixed points 

  xe = vpasolve(eq1);

% Gradient df/dx 

  df = gradient(f,[x]);

% Symbolic to numeric

  f_dash = subs(df(1),x,{xe});

% Print results to Command window

  output(r, xe, f_dash, P)

 

 

For the interval 0 < r < ¾, the eventual behaviour after many iterations is known – the population becomes extinct or is attracted to an equilibrium (fixed) population . This is called period 1 dynamics were

                 

                  

                 

                 

                

                

Simulations

 

r = 0.240000  

Dynamic period P =  1 

     xe = -0.041667   f_dash = 1.040 

     xe = 0.000000   f_dash = 0.960 

 Stable fixed points

     xe = 0.000000   f_dash = 0.960       population becomes extinct

 

r = 0.740000  

Dynamic period P =  1 

   xe = 0.000000   f_dash = 2.960 

   xe = 0.662162   f_dash = -0.960 

Stable fixed points

   xe = 0.662162   f_dash = -0.960   fixed point x1 = 0.662162

 

 

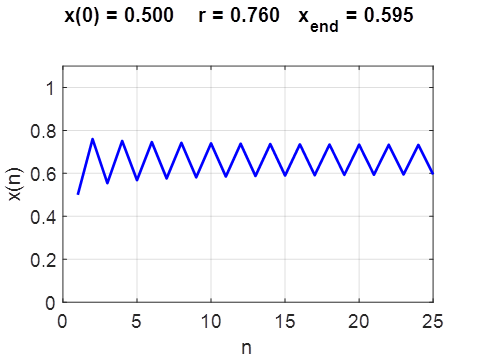
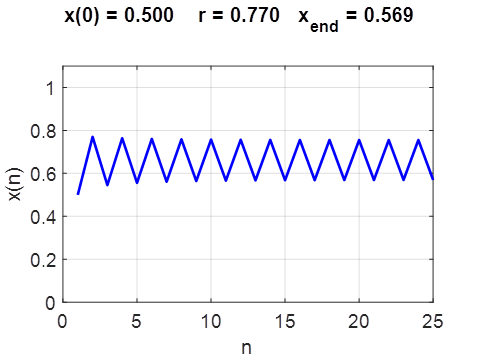
What happens when the value of r is slightly increased slightly above 3/4? We know from our observations the single fixed point becomes unstable and gives birth (bifurcates) to a cycle of period 2. The population x returns to the same value only after every second iteration

the range  ?

            

 

We can solve this set of equations to find all the fixed points  for period 2 dynamics.

 

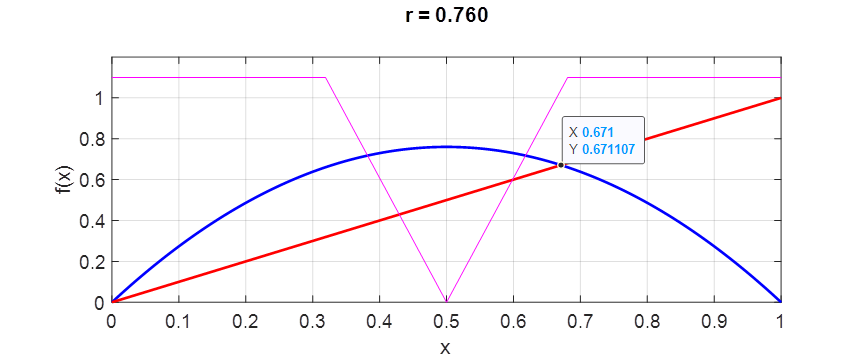
As r is increased further, eventually the magnitude of the [1D] mapping function  exceeds one, and other bifurcations occur, until the dynamics becomes chaotic.

 

Simulations

 

r = 0.760000  

Dynamic period P =  1 

 

xe = 0.000000   f_dash = 3.040 

xe = 0.671053   f_dash = -1.040        no single fixed points

 

r = 0.760000  

Dynamic period P =  2 

   xe = 0.000000   f_dash = 9.242  

  xe = 0.598356   f_dash = 0.838 

  xe = 0.671053   f_dash = 1.082 

  xe = 0.730591   f_dash = 0.838 

 

Stable fixed points

   xe = 0.598356   f_dash = 0.838 

   xe = 0.730591   f_dash = 0.838      2 fixed points

 

r = 0.862300  

Dynamic period P =  2 

   xe = 0.000000   f_dash = 11.897 

  xe = 0.440028   f_dash = -0.999 

  xe = 0.710078   f_dash = 2.100 

  xe = 0.849894   f_dash = -0.999 

Stable fixed points

   xe = 0.440028   f_dash = -0.999 

   xe = 0.849894   f_dash = -0.999       2 fixed points – period 2 “boundary”

 

r = 0.862400  

Dynamic period P =  4 

Stable fixed points

   xe = 0.437181   f_dash = 0.998 

   xe = 0.442748   f_dash = 0.998 

   xe = 0.848787   f_dash = 0.998 

   xe = 0.851093   f_dash = 0.998       4 fixed points

 

r = 0.886010  

Dynamic period P =  4 

Stable fixed points

   xe = 0.363309   f_dash = -0.999 

   xe = 0.523572   f_dash = -0.999 

   xe = 0.819792   f_dash = -0.999 

   xe = 0.884041   f_dash = -0.999     4 fixed points – period 4 “boundary”

 

r = 0.886030  

Dynamic period P =  8 

Stable fixed points

   xe = 0.362731   f_dash = 0.997 

   xe = 0.363843   f_dash = 0.997 

   xe = 0.522372   f_dash = 0.997 

   xe = 0.524814   f_dash = 0.997 

   xe = 0.819249   f_dash = 0.997 

   xe = 0.820326   f_dash = 0.997 

   xe = 0.883848   f_dash = 0.997 

   xe = 0.884256   f_dash = 0.997     8 fixed points

 

r = 0.891100  

Dynamic period P =  8 

Stable fixed points

   xe = 0.346767   f_dash = -0.999 

   xe = 0.374766   f_dash = -0.999 

   xe = 0.490614   f_dash = -0.999 

   xe = 0.554267   f_dash = -0.999 

   xe = 0.807407   f_dash = -0.999 

   xe = 0.835197   f_dash = -0.999 

   xe = 0.880603   f_dash = -0.999 

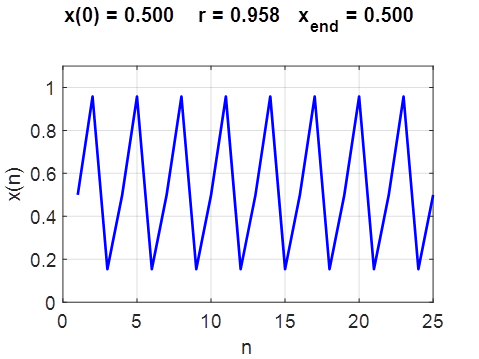
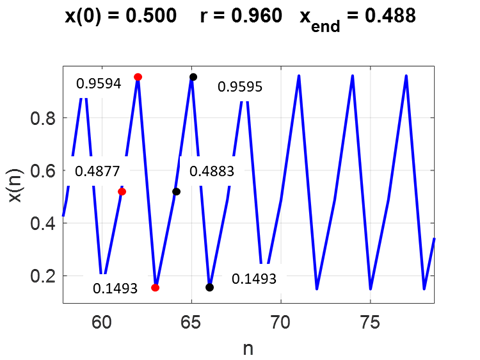
   xe = 0.890786   f_dash = -0.999       8 fixed points – period 8 “boundary”

 

 

r = 0.960000  

Dynamic period P =  3 

  xe = 0.000000   f_dash = 56.623 

  xe = 0.149407   f_dash = -0.875 

  xe = 0.169434   f_dash = 2.744 

  xe = 0.488004   f_dash = -0.875 

  xe = 0.540388   f_dash = 2.744 

  xe = 0.739583   f_dash = -6.230 

  xe = 0.953736   f_dash = 2.744 

  xe = 0.959447   f_dash = -0.875 

 

Stable fixed points

   xe = 0.149407   f_dash = -0.875 

   xe = 0.488004   f_dash = -0.875 

   xe = 0.959447   f_dash = -0.875      3 fixed points – period 3

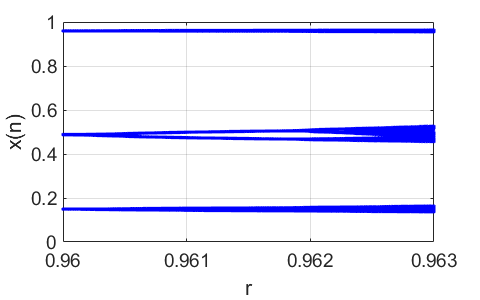
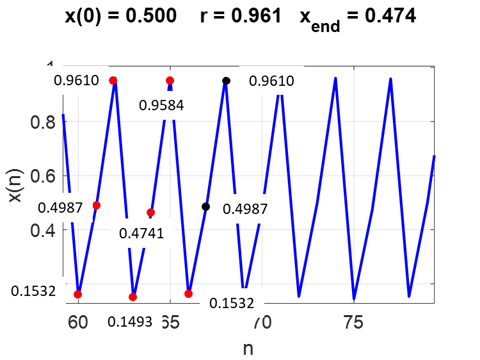
                                                                       period doubling window in chaotic region

 

r = 0.962000  

Dynamic period P =  6 

Stable fixed points

   xe = 0.144093   f_dash = 0.186 

   xe = 0.153195   f_dash = 0.186 

   xe = 0.474083   f_dash = 0.186 

   xe = 0.498668   f_dash = 0.186 

   xe = 0.958418   f_dash = 0.186 

   xe = 0.960993   f_dash = 0.186       6 fixed points – period 6  

                                                                       period doubling window in chaotic region

 

 

MATLAB

Below are segments of the code to investigate the dynamics of the one-dimensional map for the logistic difference equation.

 

chaosLogisticsEq01.m   animation x vs n and bifurcation diagram

% Initial condition   0 <= x0 <= 1

  x0 = 0.25;

 

% Control parameter 0 <= r <= 1

  rMin = 0.10;

  rMax = 0.99;

  Nr = 501;

  r = linspace(rMin,rMax,Nr);

 

% Number of iterations

  N = 100;

 

% Logistic Equation

 

  x = zeros(N,Nr);

  xEND = zeros(Nr,1);

 

  for k = 1:Nr

      x(1,k) = x0;

    for c = 1:N-1

      x(c+1,k) = 4*r(k)*x(c,k)*(1-x(c,k));

    end

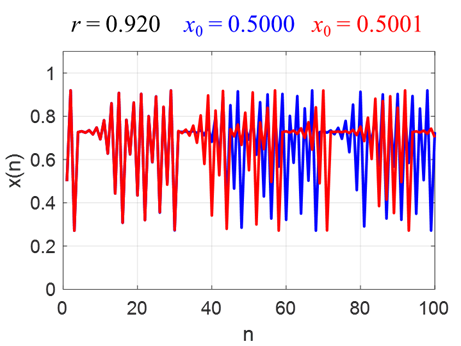
      xEND(k) = x(c+1,k);

  end

 

chaosLogisticsEq02.m       x vs n

% Control parameter 0 <= r <= 1

  r = 0.76;

 

% Initial condition   0 <= x0 <= 1

  x0 = 0.5001;

 

% Number of iterations

  N = 25;

 

% Logistic Equation

 

  x = zeros(N,1);

  x(1) = x0;

 

 for c = 1:N-1

     x(c+1) = 4*r*x(c)*(1-x(c));

 end

     xEND = x(c+1);

     xSTABLE = 1-1/(4*r);

 

 

chaosLogisticsEq03.m       [1D] logistic map function  f(x) vs x

% INPUTS ==============================================================

% Period  p = 1, 2, 4, 8

  p = 1;

 

% Control parameter 0 <= r <= 1

  r = 0.76;

 

% Number of iterations

  N = 5001;

 

% SETUP  ============================================================= 

% Population

x = linspace(0,1,N);

  dx = x(2) - x(1);

 

% Logistic Difference Equations for period doubling

  f1 = iterate(x,r);

  f2 = iterate(f1,r);

  f3 = iterate(f2,r);

  f4 = iterate(f3,r);

  f5 = iterate(f4,r);

  f6 = iterate(f5,r);

  f7 = iterate(f6,r);

  f8 = iterate(f7,r);

 

  if p == 1; f = f1; end

  if p == 2; f = f2; end

  if p == 4; f = f4; end

  if p == 8; f = f8; end

 

% Gradient df/dx

  gradF = gradient(f,dx);

 

% FIXED POINTS: Intersection points x and f(x)  

  interSections = find(abs(f-x) <= 0.001);

%  xIS = x(interSections);

 

  n = 0; xe(1) = 0;

  for c = 1 : length(interSections)

   if abs(gradF(interSections(c))) < 1

     n = n+1;

     xe(n) = x(interSections(c));

   end

  end

 

 

 

The logistic difference equation is an exceptionally simple model of the population growth for   butterflies who lay eggs their eggs in year n and their offspring are born in year .  If there are zero butterflies  then no butterflies and no eggs, hence . At the other extreme, , then the competition for food is so great that they do not lay eggs, so again .

 

References

 

http://www.people.vcu.edu/~hsedagha/Sedaghat-CRC_Handbook.pdf

 

H. Gould & J. Tobochnik   An Introduction to Computer Simulation Methods (Part 1)

 

R. M. May Simple Mathematical Models with Very Complicated Dynamics, Nature 261, 459 (1979)