DOING PHYSICS WITH MATLAB

 

A NUMERICAL APPROACH TO THE PHYSICS OF THE ENVIRONMENT AND CLIMATE

Ian Cooper

matlabvisualphysics@gmail.com

 

THE VERTICAL PROFILE OF THE ATMOSPHERE

 

MATLAB

Download directory

                   https://drive.google.com/drive/u/3/folders/1j09aAhfrVYpiMavajrgSvUMc89ksF9Jb

                   https://github.com/D-Arora/Doing-Physics-With-Matlab/tree/master/mpScripts

 

Scripts

    climate.m

    The atmospheric temperature profile data is stored in the vectors ZD and TD.

    Using this data, the pressure and density profiles are calculated and plotted.

 

 

MODEL PARAMETERS: symbol   quantity   [value  units]

 

m                mass of a parcel of air                           [kg]

n                 number of moles                                    [mol]

N                number of molecules                             [ - ]

M               molar mass                                             [kg.mol-1]

MA             molar mass dry air                                 [MA = 0.029 kg.mol-1]

Mw             molar mass water vapour                     [Mw = 0.018 kg.mol-1]

x, y, z         Cartesian coordinates                            [m   km]

u, v, w        Cartesian velocity components            [m.s-1]

V                volume                                                    [m3]

dV              volume element                                     [dV = dx dy dz]

               density of air parcel                               [kg.m-3]

             dry air density                                        [ = 1.29 kg.m-3   T = 0 oC = 273 K]

                                                                                   [ = 1.19 kg.m-3   T = 25 oC = 288 K]

T                temperature                                            [K   oC]

p                 pressure                                                  [Pa  hPa]

            change in internal energy                     [J]

W               work                                                        [J]

Q                heat exchanged with system                 [J]

p0               atmospheric pressure at

                   Earth’s surface                                       [p0 = 1013.25 hPa = 1.01325x105 Pa]

g                 acceleration due to gravity                   [m.s-2]

g0               acceleration due to gravity

                   at Earth’s surface                                   [g0 = 9.80665 m.s-2]

R                Universal gas constant                          [R = 8.314 J.K-1.mol-1]

Rd                   gas constant dry air                               [Rd = 287 J.K-1.kg-1]

kB               Boltzmann constant                              [kB = 1.38065x10-23  J.K-1] 

NA             Avogadro’s number                              [NA = 6.02214 molecules. mol-1]

cpd              constant-pressure specific heat

                    for dry air                                              [cpd = 1004.65805 J.kg-1.K-1]

ME             mass of Earth                                         [ME = 5.9722x1024 kg]

RE              radius of Earth                                       [RE = 6.3743x106 m]

G                Gravitation constant                             [G = 6.67408 x10-11 N.m2.kg-2]

 

 

THE ATMOSPHERE

 

The atmosphere contains a few highly concentrated gases, such as nitrogen (78%), oxygen (21%), and argon (0.93%), carbon dioxide (0.035%) and many trace gases, such as methane, ozone and nitrous oxide. To a good approximation the gases of the atmosphere can be assumed to obey the laws for an ideal gas.

 

The most characteristic feature of the atmosphere is its vertical temperature distribution profile. From the ground up to a mean altitude of 11 km (8 km at the poles and 17 km at the equator) lies the troposphere. Nearly all meteorological phenomena occur within this layer (wind, cloud formation and precipitation). Above the troposphere is the stratosphere (~11 km to ~ 50 km) where airflow is primarily horizontal. The narrow layer separating the troposphere and stratosphere is called the tropopause. Beyond the stratosphere is are the layers stratopause (~ 50 km), mesosphere (~50 km to ~90 km), mesopause (~90 km) and the thermosphere (> ~90 km).

 

The temperature profile of the atmosphere is shown in figure 1. The figure is generated using the Matlab script climateG.m using the temperature data from Fundamentals of Atmospheric Modelling by Mark Z. Jacobson

 

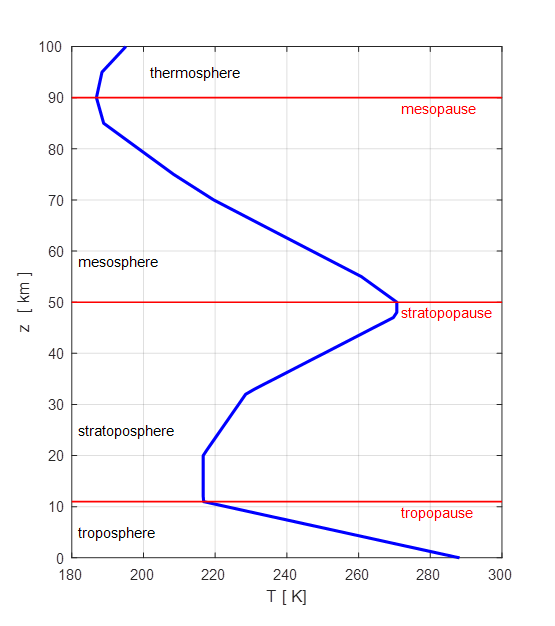
     Fig. 1.   Vertical temperature profile of the atmosphere. (Script climateG.m)

 

Other important characteristics of air are its pressure and density. These parameters vary with altitude, latitude, longitude, and season. Using the equation for an ideal gas, it is possible to calculate the vertical profiles of the pressure and density numerically from the temperature profile.

 

Consider a parcel of air in static equilibrium as shown in figure 2. The forces acting upon the parcel are the gravitational force FG and the pressure gradient force FP such that the net force is zero .  The pressure gradient force at any altitude is due to the weight of the entire column of air vertically above it.

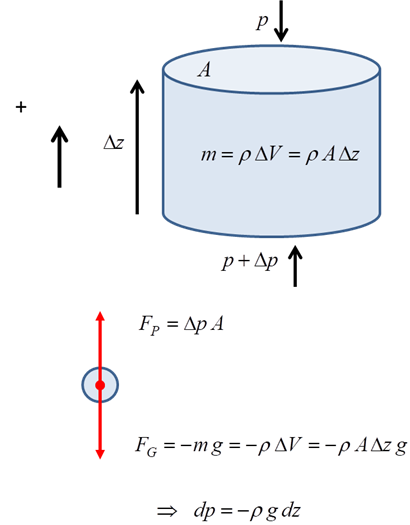
     Fig. 2.  Forces acting on a parcel of air.

 

Hence, the vertical pressure gradient is

(1)     

 

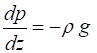
and the horizontal pressure at any altitude is a constant. Equation (1) is known the hydrostatic equation. Since the density  is a function of altitude, we need to express the density as a function of temperature T.

 

The equation of state for an ideal gas describes the relationship among pressure, volume, and absolute temperature.

 

  (2)     

 

                

 

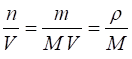
 (3)   

 

 

Combining equations (1) and (3), we obtain

 

     (4)    

 

 

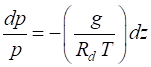
Equation (4) can be solved to find the variation in pressure and density as functions of altitude. However, equation (4) is difficult to solve since the temperature T is also a function of altitude z.  Often many approximations are used to find a solution to equation (4) such as assuming T = constant.  Equation (4) can be solved using numerical methods to directly integrate the equation from the Earth’s surface (p = p0, z = 0) to an altitude z.

    

                   

 

                

 

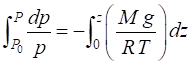
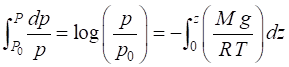
     (5)    

 

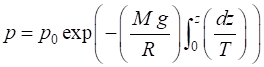
Once the variation of pressure with altitude is known, then the variation in density is given by

 

     (3)    

 

 

To evaluate equation (5), the published data* for the variation in temperature T with altitude z is used.  Part of the Script climateG.m to evaluate equation (5) is

 

  num = length(zD);

          PD = zeros(num,1);

          PD(1) = p0;

          for c = 1:num-1

            PD(c+1) = PD(c) * exp((-2*gD(c)./R_d)*(zD(c+1)-zD(c)) / (TD(c+1) + TD(c)));

         end

         rhoD = PD./(R_d.*TD'); 

 

zD and TD are the vectors for the published data*.

 

*   Fundamentals of Atmospheric Modelling by Mark Z. Jacobson

 

The acceleration due to gravity g is also a function of altitude z and is calculated from Newton’s Law of Gravitation

 

     (6)     

 

The change in g with z is insignificant since z << RE.

 

Figures 3 and 4 show the variation in the acceleration due to gravity, atmospheric temperature, atmospheric pressure and density as functions of altitude.

 

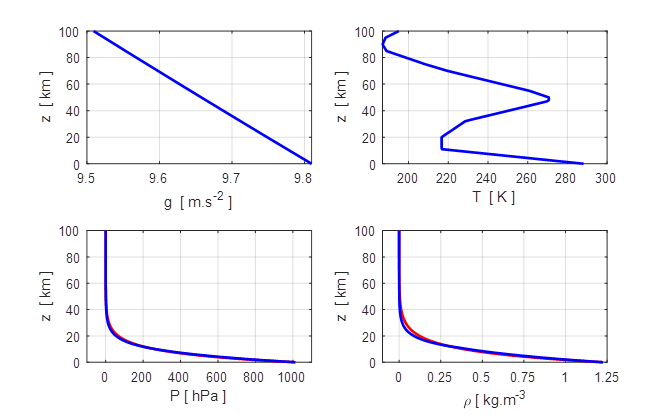
 Fig. 3.   Variation of the acceleration due to gravity g, temperature T, pressure P and density with altitude z. The red curves in the pressure and density show that there is an excellent fit for exponential decreases in both the pressure and density with altitude.

 

Fig. 4.   Variation of the acceleration due to gravity g, temperature T, pressure P and density with altitude z in the troposphere.

 

 

The pressure diagram shows air in the atmosphere is concentrated in a thin shell above the Earth’s surface.

                       99.7% atmosphere below 40 km

                       95%   atmosphere below 20 km

                       74%  atmosphere below 10 km

                       47% atmosphere below 5 km

 

In figure (3) exponential decay curves (red) were added to the plots for the pressure and density. The Matlab Curve Fitting Tool was used to find the exponential equations for the fits

         

 

where H is known as the scale height.

 

 

Pressure                     

 

Density                       

 

 

We can now easily estimate the mass Matm of the atmosphere

          At the Earth’s surface    

                                

 

 

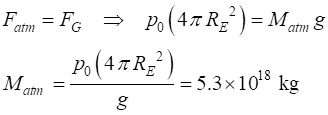
In the troposphere the temperature falls linearly with increasing altitude

         

 

where  is the surface temperature and  is the vertical thermal lapse rate.

 

The values for the T0 and Lenv (environmental lapse rate) as shown in figure 4 are calculated using the Matlab function fitlm

 

  F = find(zD>1e4,1);

  F = 1:F;

  LR = fitlm(zD(F),TD(F))

  Lcoeff = LR.Coefficients.Estimate

  Lintercept = Lcoeff(1)

  Lslope = Lcoeff(2)*1e3

 

The results are:   T0 = 288 K and Lenv = - 6.49 K.km-1

 

We can calculate the dry air lapse rate using the first law of thermodynamics and the ideal gas equations. The first law of thermodynamics states that when heat Q is exchanged with an isolated system, the system does work W and the internal energy of the system changes (when there is a change in the internal energy of the system, its temperature changes).

 

               

 

Consider a parcel of air that is displaced upward without any exchange of heat with the surrounding air Q = 0. This process when Q = 0 is called adiabatic. Since the pressure decreases with height, the parcel of air will expand and do work on its surroundings which results in a fall in its temperature and decrease in its internal energy.

 

      For an adiabatic process       

 

                  

 

 

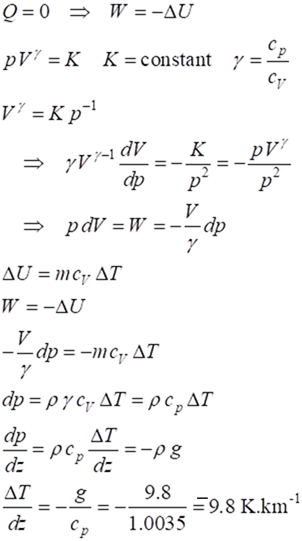
The adiabatic dry air lapse rate within the troposphere is -9.8 K.km-1. The adiabatic dry air lapse rate has a larger magnitude than the environmental lapse rate -6.5 K.km-1. With humid air the lapse rate varies between – 5 to -10 K.km-1.