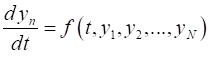DOING PHYSICS WITH MATLAB

 

RUNGA-KUTTA FOURTH-ORDER METHOD

     Numerical Solution of Ordinary Differential Equations

     Initial Value Problems

 

Ian Cooper

Any comments, suggestions or corrections, please email me at

matlabvisualphysics@gmail.com

 

 

 

MATLAB

DOWNLOAD DIRECTORY FOR SCRIPTS

 

da_RK01.m

     Solutions of ODE of the form 

da_RK02.m

     Solutions of ODE of the form 

da_RK03.m

     Sets of First-Order ODEs               

da_RK04.m

     Second-Order ODEs               

     Damped harmonic oscillator

 

 

RUNGE-KUTTA METHOD

The purpose of the Runge-Kutta method is to obtain an approximate numerical solution of an ordinary differential equation given a set of initial conditions. The Euler method is in general not recommended for solving ordinary differential equations (ODEs) because it is not very accurate compared to other methods run at the same step size and is not always stable. The fourth-order Runge-Kutta method described below is adequate for most practical applications.

 

Problems involving ODEs can always be reduced to the study of sets of first-order differential equations. The generic problem in ODEs is thus reduced to the study of a set of N coupled first-order differential equation for the functions yn, n = 1, 2, 3, … , N having the form

        (1)       

 

where the functions on the right-hand side are known. The goal is to find the unknown yn values. The solutions of equation 1 depend upon the boundary conditions applied (known values of the function yn). Only initial value problems where all the yn values are given at some starting value ts are considered.

 

The fourth-order Runge-Kutta method is based upon solving a system of equations at each time t with time step h (h = constant is only considered. You can include an adaptive step size algorithm is greater accuracy is required.

         (2A)       

         (2B)       

         (2C)       

         (2D)       

         (2E)       

         (2F)       

         (2G)      

 

In each time step the derivative is evaluated four times: once at an initial point and once at the end point and twice at the mid-point.

The Runge-Kutta is not the best and most accurate ODE integrator, but is OK for most applications and is very easy to incorporate into a Script. An advantage of the method is that it is self-starting – requires only a value of the function at a single previous point to obtain functional values ahead. Also, it is easy to change the step size h at any step in the computation.

 

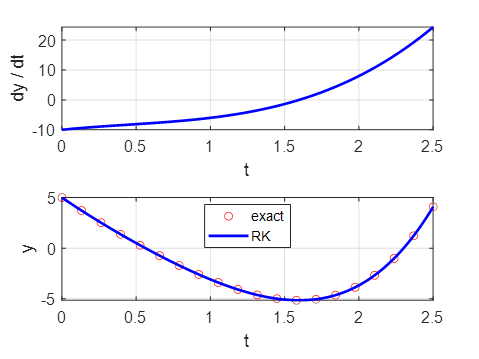
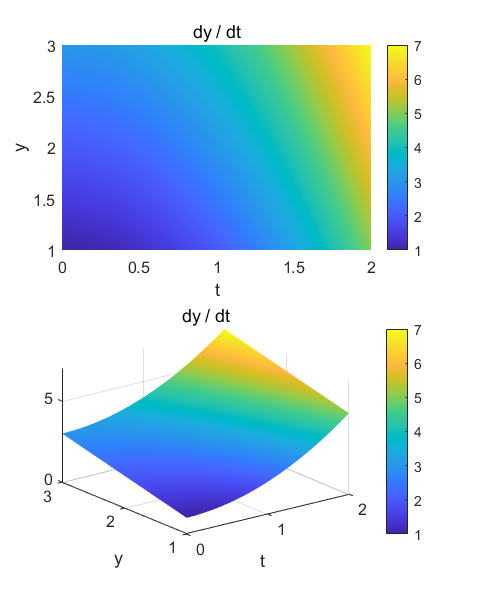
Example 1           da_RK01.m

 

                         y(0) = 5

 

Exact solution

                

 

 

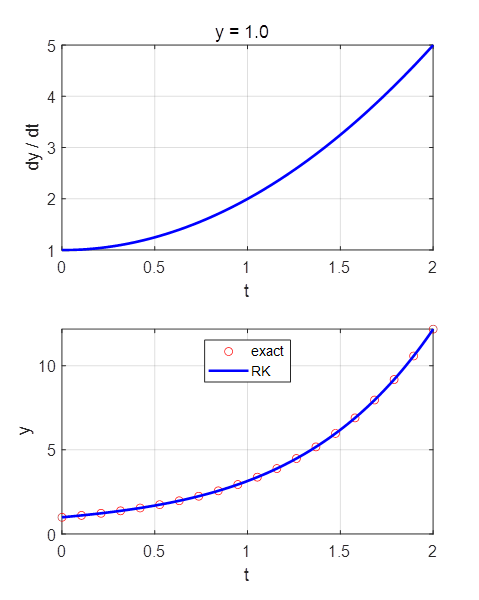
You can vary the step size h to find out the largest value of h that still gives an accurate result.

 

 

Example 2          da_RK02.m

                   

Exact solution

          

 

The ODE is given as a Matlab function. The function can easy be changed.

       function f = YDOT(t,y)

       %   f = t + y;

           f = t.^2 + y;

       end

 

The input parameters are given in the Input section of the Script

% >>>>>  Number of grid points

  N = 200;

 

% >>>>>  t variable

  tMin = 0;

  tMax = 2;

 

% >>>>>  initial value for y variable

  y = zeros(1,N);

  y(1) = 1;

 

 

The ODE is solved in the Setup section of the Script

% SETUP  ============================================================== 

% t interval and step size

  t = linspace(tMin,tMax,N);

  h = t(2) - t(1);

% yDot variable as a function of t at y(nY) (calls function YDOT)  

  nY = 1;

  yDot = YDOT(t,y(nY));

 

% Compute y and yDdot values as a function of time =====================

for n = 1 : N-1

   k1 = YDOT(t(n),y(n));

   k2 = YDOT(t(n) + 0.5*h,y(n)+k1*h/2);

   k3 = YDOT(t(n) + 0.5*h,y(n)+k2*h/2);

   k4 = YDOT(t(n) + 1.0*h,y(n)+k3*h);

 

   y(n+1) = y(n) + h*(k1+2*k2+2*k3+k4)/6;

end

 

% yDot variable (calls function YDOT) 

  yDot = YDOT(t,y(1));

 

 

 

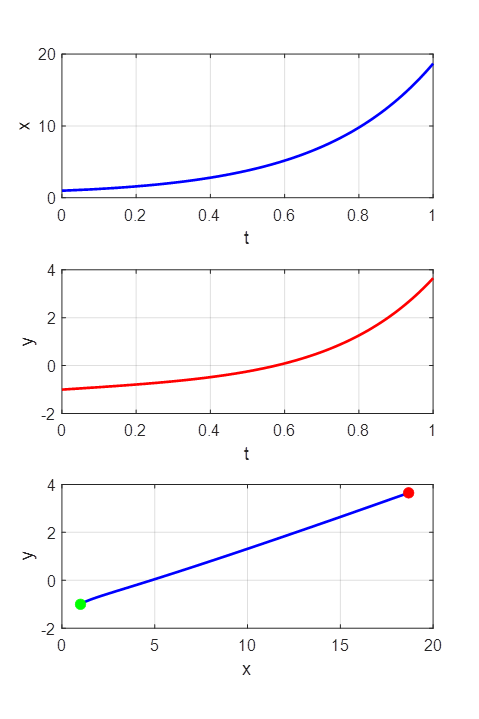
Example 3                da_RK03.m

   Sets of First-Order ODEs               

 

The Runge-Kutta method can be used to find the solutions of sets of first-order ODEs. In this example there are two coupled ODEs. But the method can be extended to larger numbers of equations.

 

 

       

        

       

       

      

       

    

    

    

    

    

    

 

 

Example 4        da_RK04.m

Higher-order ODEs      

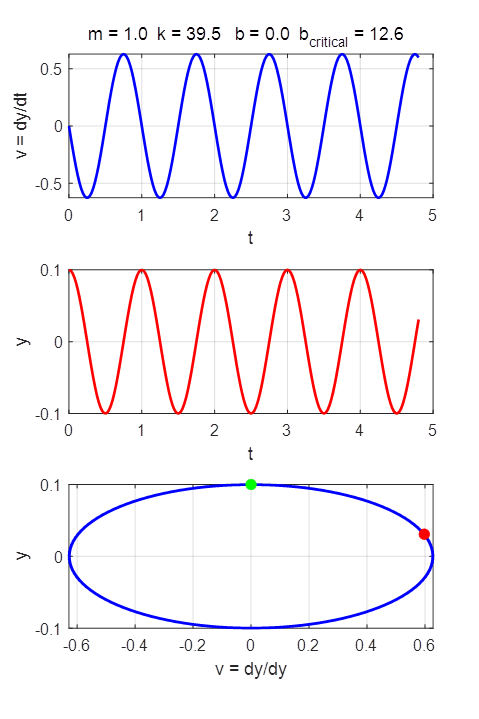
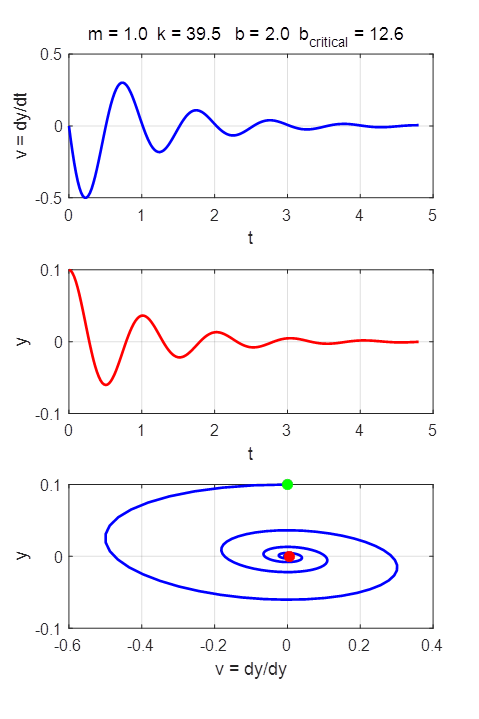
Higher-order ODEs can be treated as if they were sets of first-order ODEs (Example 3). We will consider the second-order equation of a damped harmonic oscillator.

        

       

 

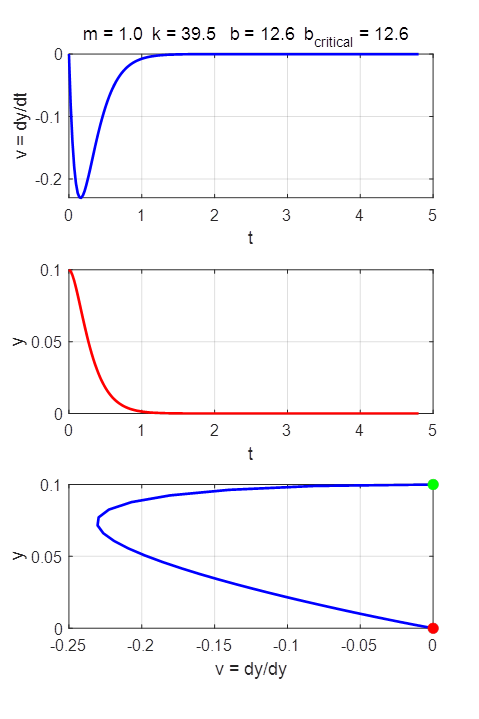
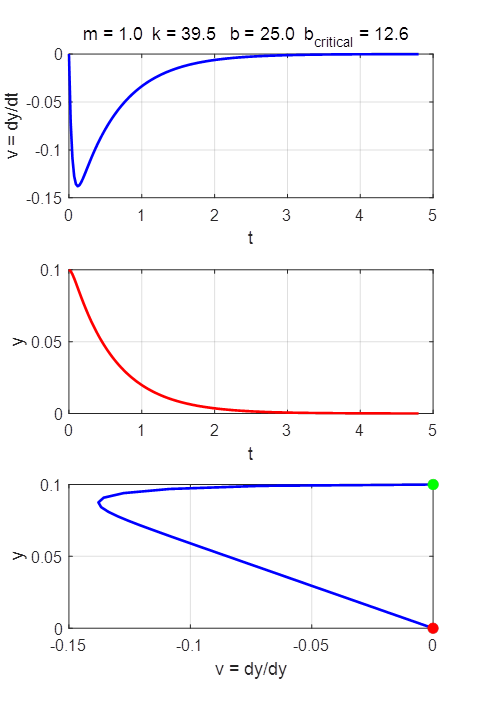
where m is the mass of the oscillator, k is the spring constant, and b is the damping constant. The variable y(t) is the displacement of the oscillator from the equilibrium position (y = 0) and v(t) is the velocity of the oscillator . 

 

The period of oscillation is  and the critical damping factor is .

 

The constants m, k and b and the initial conditions can be changed in the INPUT section of the Script.

 

We make the substitution   to get two coupled first-order ODEs

      

 

The solutions of the ODE by the Runge-Kutta method for different input parameters are shown in the following figures:

NO DAMPING

 

UNDERDAMPING

 

CRITICAL DAMPING (shortest time to equilibrium with)

 

OVERDAMPED