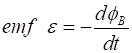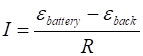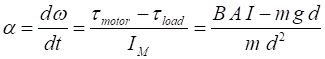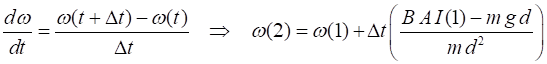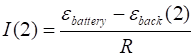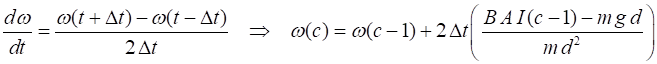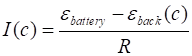Matlab Physics

HOW A MOTOR WORKS IN LIFTING A LOAD

spMotors.m

The script is used to calculate and graph the parameters that are essential in describing the physics of a simple DC motor in lifting a load vertically from rest to when it rises with a constant velocity. The motion of the load is computed using a finite difference method to calculate the angular speed of the motor as a function of time. The main variable to change in running the script is the mass of the load. The mass is changed within the script, but the program could be modified to enter the mass through the Command Window or the Live Editor.

INTRODUCTION

Motors and generators are very similar as they have the same construction (rotating coil in a magnetic field). Generators convert mechanical energy into electrical energy - when the coil is turned: the magnetic flux changes, and an emf is induced and for a complete circuit an induced current is generated. A motor converts electrical energy into mechanical energy – the coil carrying the current experiences a torque which is responsible for why the coil rotates. 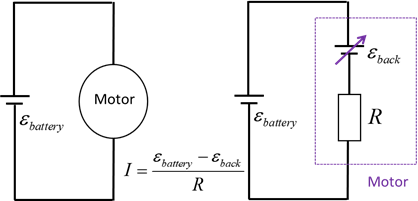However, the motor acts as a generator whenever its coil rotates. Therefore, when the coil of the motor is rotating, an emf is generated. This self-generated emf is called the back emf. Lenz’s law tells us this back emf will oppose the change that created it, so that the battery emf that powers the motor will be opposed by back emf of the motor.

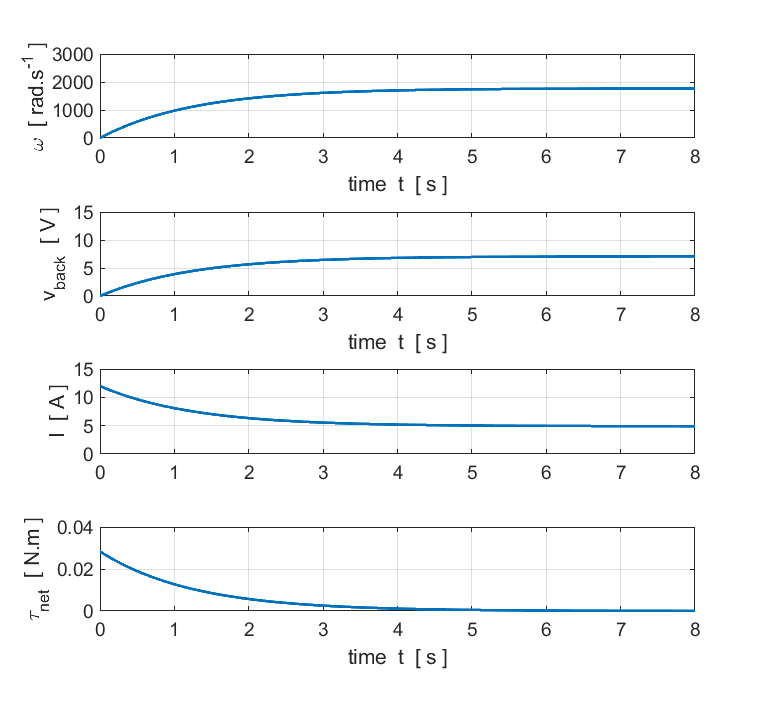
Faraday’s law of electromagnetic induction is

For a single coil of cross-sectional area A rotating in a uniform and constant magnetic field B, the induced emf is

Thus, the back emf is proportional to the motor’s angular speed (rotation speed) .

The motor’s current is

When the motor is first switched on, the coil has zero angular speed, and the back emf is zero, so the current through the motor is a maximum. As the motor turns faster and faster, the back emf increases, always opposing the battery emf, and reduces the voltage across the coil and the current it draws. Thus, when a motor first comes on, it draws more current than when it runs at its normal operating speed. When a mechanical load is placed on the motor, the back emf drops, more current flows, and more work can be done. If the motor runs at too low a speed, the larger current can overheat it due to ohmic heating , perhaps even burning it out. If there is zero mechanical load on the motor, the angular velocity will increase until the back emf is nearly equal to the driving emf and the motor will use only enough energy to overcome friction.

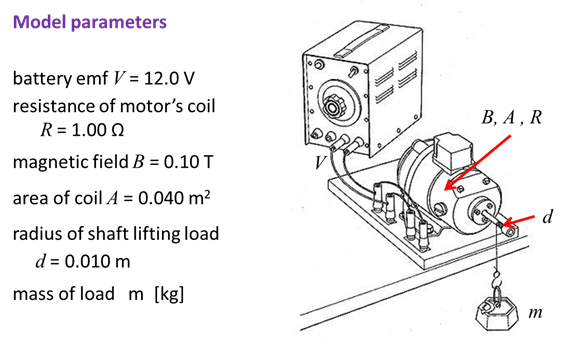
The single coil with cross-sectional area A in the magnetic field B of a simple DC motor with current I will experience a torque due to the magnetic force acting on a current element. The torque is given by

SIMULATIONS

Consider a simple DC motor that is used to lift a load as shown in the diagram.

A string is attached to the load mass m and wound around the motor’s axle (shaft) which has a radius d. The motion of the load of is determined by the net torque acting to lift the load

where is the moment of inertia and is the angular acceleration of the rotating axle of the motor.

The torque due to the gravitation force is and the maximum torque provided by the motor is . The equation of motion for the load can be expressed as

We solve the equation of motion for the angular speed using a finite difference approximation:

Initial values – 1^st time step (t = 0 index = 1)

2nd time step (index = 2)

At the next sequence of time steps c = 3, 4, …. ,

After the calculation of the angular speed, back emf and current we can then calculate the power supplied by the battery, dissipated in the resistor (ohmic heating) and power from the motor to lift the load and show that energy is conserved by the system of the battery, motor and load.

N.B. It is the power provided by the motor generated by the induced voltage that gives the back emf that is used to lift the load.

RESULTS

The results are displayed graphically in a Figure Window and a summary of numerical values for the times at which the load is being lifted with a constant velocity is displayed in the Command Window.

LOAD m = 0.080 kg

mass of load m = 0.08 kg

torqueL = 0.0078 N.m

torqueM = 0.0078 N.m

Icoil = 1.96 A

back emf = 10.0380 V

omega = 2509 rad/s

Pbattery = 23.54 w

Presistor = 3.85 W

Pmotor = 19.69 W

Consider the time interval from t = 6.0 s to t = 7.0 s

The axle of the motor turns through an angle in this time interval

The length h of the string wound on the axle of the motor (radius of axis ) and hence the distance the load is raised is

The increase in potential energy of the load is

The rate at which the load potential energy increases is

Therefore,

the energy to lift the motor comes from the induced emf (back emf)

created by the rotation of the coil through the magnetic field of the motor.

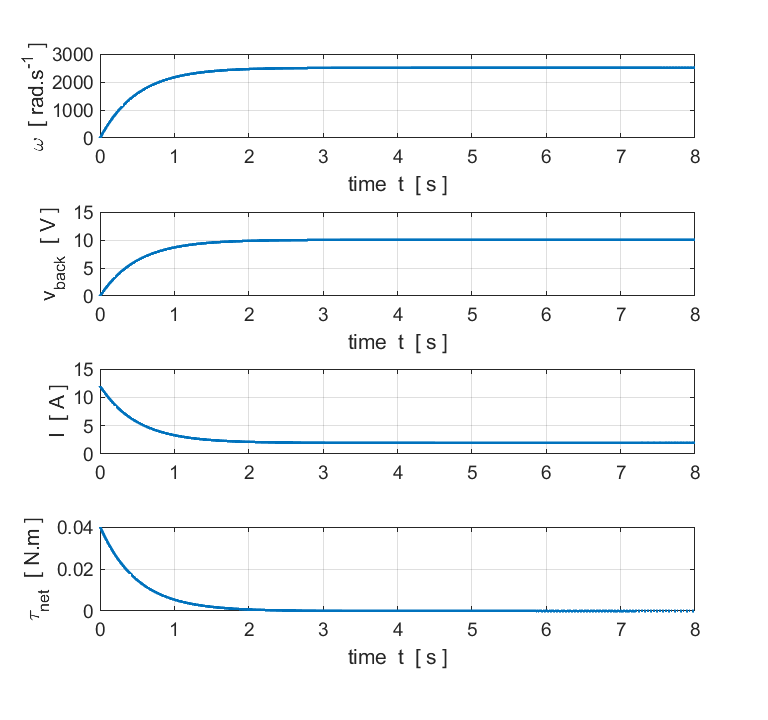
LOAD m = 0.100 kg

mass of load m = 0.100 kg

torqueL = 0.0098 N.m

torqueM = 0.0098 N.m

Icoil = 2.45 A

back emf = 9.5475 V

omega = 2387 rad/s

Pbattery = 29.43 w

Presistor = 6.01 W

Pmotor = 23.42 W

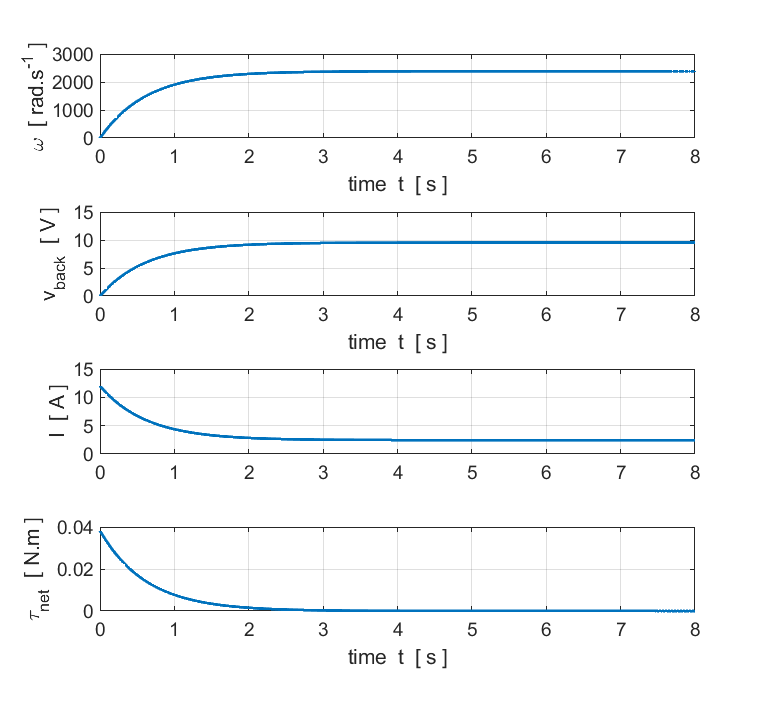
LOAD m = 0.200 kg

mass of load m = 0.200 kg

torqueL = 0.0196 N.m

torqueM = 0.0196 N.m

Icoil = 4.90 A

back emf = 7.0950 V

omega = 1774 rad/s

Pbattery = 58.86 w

Presistor = 24.06 W

Pmotor = 34.80 W

Summary of steady state values
mass m [kg]	0.08	0.10	0.20
[N.m]	0.0078	0.0098	0.0196
coil current I [A]	1.96	2.45	4.90
induced emf [V]	10.04	9.55	7.10
angular speed [rad.s^-1]	2.51x10³	2.39x10³	1.77x10³
P_battery [W]	23.54	29.43	58.86
P_resistor [W]	3.85	6.01	24.06
P_motor [W]	19.69	23.42	34.80
P_resistor + P_motor[W]	23.54	23.42	58.86
lifting load P_G [W]	19.69	23.42	34.80
Larger the load lower the rotation speed smaller the back emf greater the current greater energy dissipated by resistor why motors burn out if when motor spins slower than at its normal speed. Energy is conserved (assuming no energy losses due to friction or other dissipative forces other than through ohmic heating).