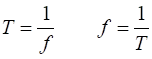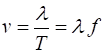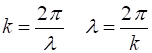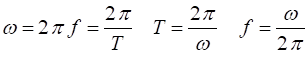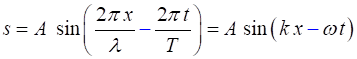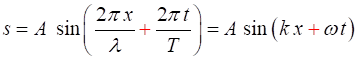VISUAL PHYSICS ONLINE

WAVES

WAVE MOTION

Most information about our surroundings arrives as a wave: sounds are transpoted to our ears; light to our eyes and electromagnetic radiaiton to our mobile phones. Through wave motion, energy can be transferred from a source to a receiver without the transfer of matter between the two points.

A good visual example are the waves on the surface of water. When a stone is dropped into a lake, waves will be generate that travel outwards in expanding circles, with the centres as the source of the disturbance. The wave propagates, not the water.

Fig.1. Snap shot of the waves on the surface of water.

At each point, the water bobs up an down. The shape of the wave

can be approximated by a sine curve.

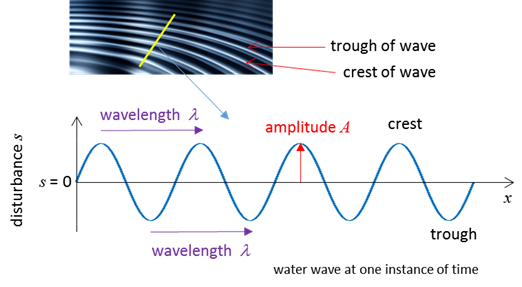
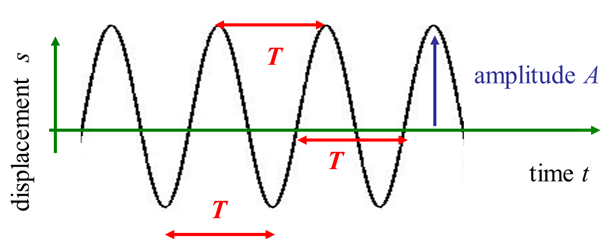
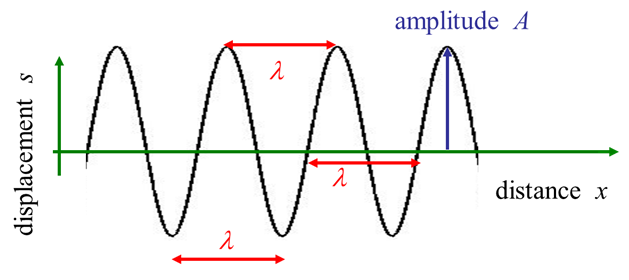
DESCRIBING WAVES

Consider a simple model for the propagation of a wave along the X axis which is represented pictorially as a sine function that depends both on time and position . The high points on the sine wave are called crests and the low points are called troughs as shown in figure 1.

The amplitude of the wave is the maximum disturbance of the wave from the mid-point between the crest and trough to either the top of the crest or to the bottom of a trough. The amplitude is a positive number. A loud sound has a large amplitude, whereas a weak radio signal has a small amplitude. Approximately the energy carried by a wave is proportional to the square of the wave amplitude.

The wavelength is the distance between two adjacent crests or two adjacent troughs or between any two successive identical parts of the wave.

The frequency of the wave is the number of vibrations each part of the wave undergoes in one second.

1 kHz = 10³ Hz (kilo) 1 MHz = 10⁶ Hz (mega) 1GHz = 10⁹ Hz (giga)

The period is the time interval for one complete vibration.

(1)

AM radio waves are broadcast in the kHz range

FM radio waves are broadcast with MHz frequencies

Microwaves have GHz frequencies

Audible sounds are generally in the range from ~ 1 Hz to < 20 kHz

The energy carried by a wave is approximately proportional to the square of the wave frequency. The higher the frequency the higher the transfer of energy in a given time interval.

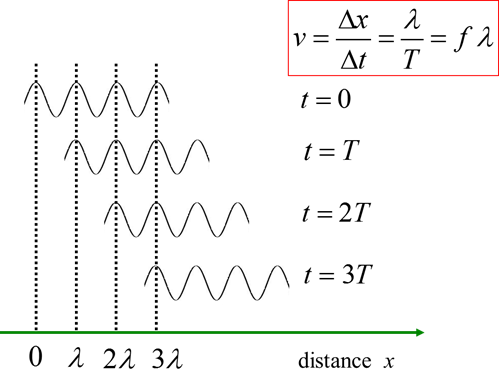
The speed of a wave is related to its wavelength and its period (frequency). The wave advances 1 wavelength in a time interval of 1 period, therefore,

(2) propagation speed of the disturbance

This relationship holds true for all types of waves, whether they are water waves, sound waves, waves on strings or electromagnetic waves.

It is mathematically very convenient to define two other quantities in describing waves: the wave number or propagation constant and the angular frequency .

(3) wave number of propagation constant [ rad.m^-1 ]

(4) angular frequency [ rad.s^-1 ]

The shape of a sinusoidal wave is given by

(5a)

wave travelling to the right (+ X direction)

(5b)

wave travelling to the left (- X direction)

The symbol is used to describe the shape of the wave and is called the wave function which depends upon the two variables, position and time . This symbol is not commonly used – the wave function is mostly given by the Greek letter (psi). N.B. could use cos instead of sin.

The term or its equivalents is called the phase of the wave. The velocity of the wave is often called the phase velocity, since it describes the velocity of the shape (phase) of the wave.

Equations 5a and 5b describe a travelling sinusoidal wave (harmonic wave). Because the wave function depends both on time and position, it is impossible to draw a simple graph of the wave function. The function must be animated or shown as a graph at a fixed time or a graph showing the variation with time at a fixed location.

Fig. 2a. A harmonic wave: at any position , the disturbance

is a sinusoidal function of time .

Fig. 2b. A harmonic wave: at any time , the disturbance

is a sinusoidal function of position .

Fig. 3. Wave or propagation velocity (phase velocity) .

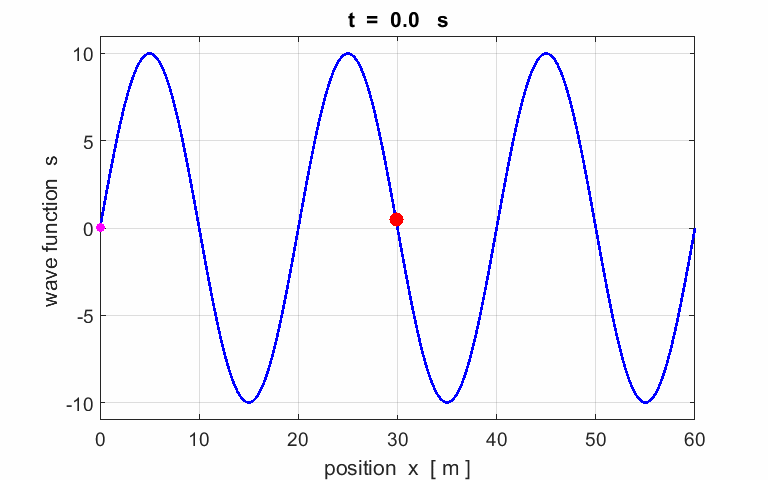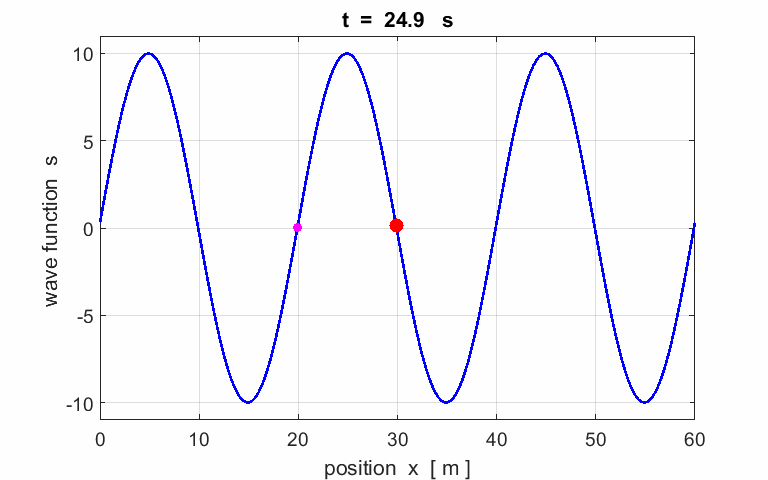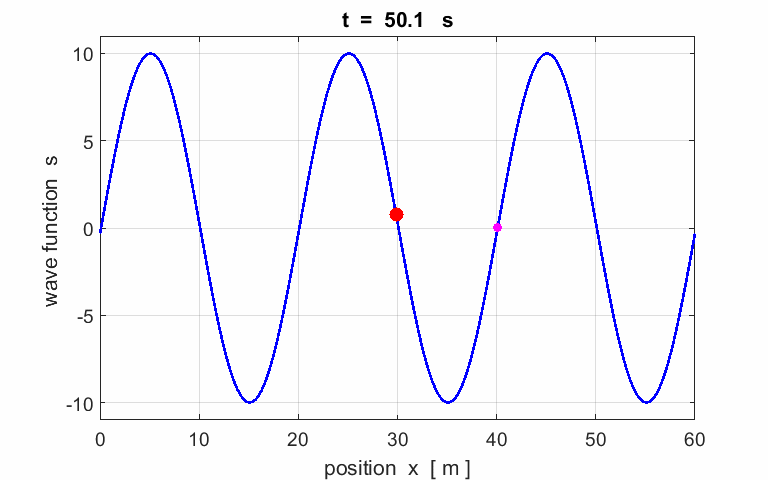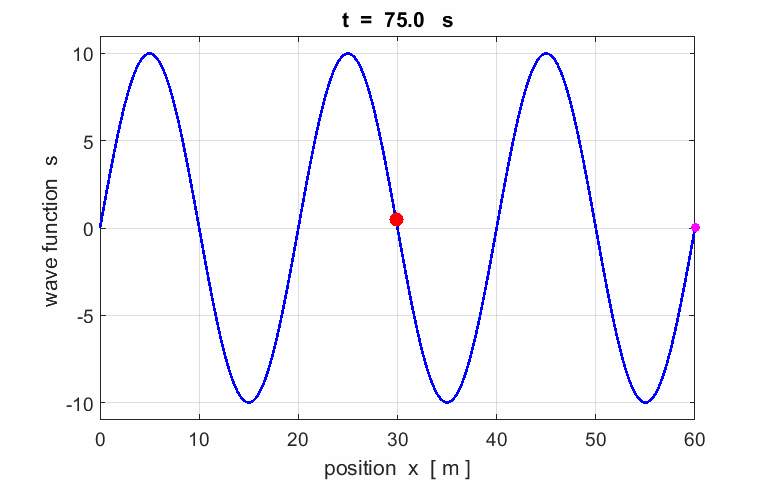
Exercise

Calculate the following parameters from the animation of a travelling wave:

amplitude wavelength period phase velocity

frequency angular velocity wave number

Describe the motion of the particle (red) located at m.

TRANSVERSE and COMPRESSIONAL (LONGITUDINAL) WAVES

Many types of waves can be classified as transverse waves or longitudinal (compressional) waves.

Transverse wave – the particles of the medium vibrate up and down in a direction transverse (perpendicular) to the motion of the wave.

Examples: waves on a stretched string, electromagnetic waves.

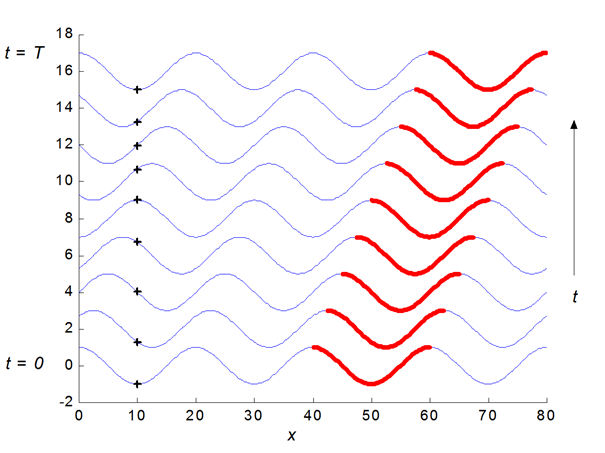
Fig. 4. Transverse wave – the particle marked + moves up and down

executing simple harmonic motion. The wave advances 1 wavelength

in a time interval of 1 period.

Fig. 5. Animation of a travelling transverse wave moving to the right.

Each particle executes SHM as they move up and down at right angles

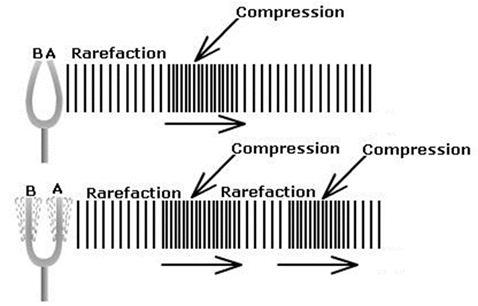
to the propagation direction.

Longitudinal (compressional) wave – the vibration of the particles of the medium vibrate along the same direction as the wave is propagating. The wave is characterised by a series of alternate condensations (compressions) and rarefactions (expansions). The plots in figure 2 also represent a longitudinal wave - the wave function gives the displacement in the direction the wave is travelling. The compressions correspond to the crests and the rarefactions are the troughs.

Example: sound waves in air.

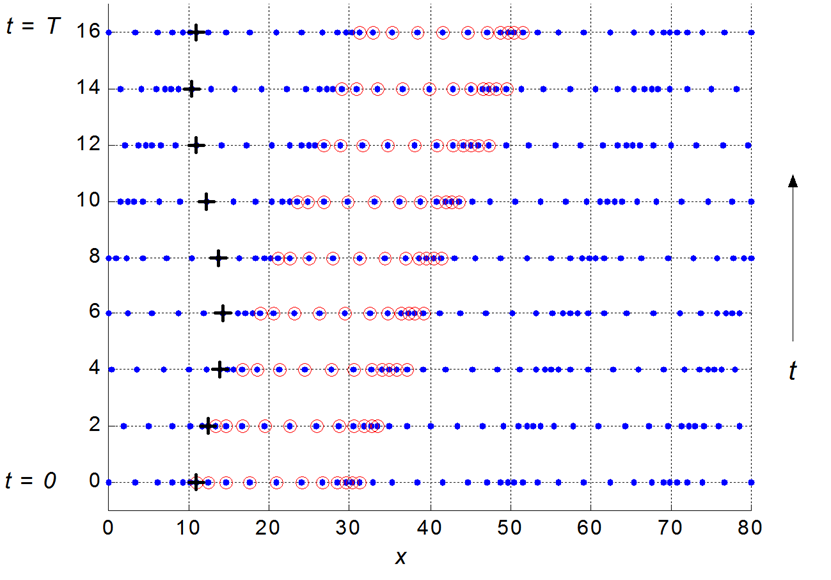
Fig. 5. Longitudinal wave – the particle marked + moves backward and

forward executing simple harmonic motion. The wave advances

1 wavelength in a time interval of 1 period. The particles oscillate over

very small distances, whereas the wave itself propagates over much larger

distances. The wavelength is the distance between adjacent compressions

or between adjacent rarefactions.

Motion along a slinky

Sound wave generated by a tuning fork

Sound wave travelling through the air

Earthquakes

Both transverse and longitudinal waves are produced when an earthquake occurs.

S waves (shear waves) ~ 5 km.s^{-1 –} transverse waves that travel through the body of the Earth. However, they can’t pass through the liquid core of the Earth.

P waves (pressure waves) ~ 9 km.s^{-1 –} longitudinal waves that travel through the body of the Earth. Only longitudinal waves can travel through a fluid, because any transverse motion would experience zero restoring force since a fluid is readily deformable. Since P waves are detected diametrically across the Earth, but not S waves, infers that the Earth’s core must be liquid.

L waves (surface waves) – travel along the Earth’s surface. The motion is essentially elliptical (transverse + longitudinal). These waves are mainly responsible for the damage caused by earthquakes.

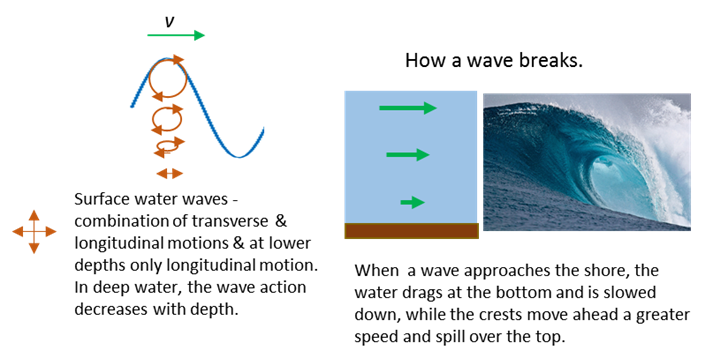
Water waves

A water wave is a surface wave that moves along the boundary between the water and the air. The motion of each water molecule at the surface is elliptical and so is a combination of transverse and longitudinal motions. Below the surface, the motion is only longitudinal.

Tsunami

Tsunami is the name given to the very long waves on the ocean generated by earthquakes or other events which suddenly displace a large volume of water. "Tsunami" is from "harbor wave" in Japanese. A tsunami is distinct from ordinary wind-driven ocean waves in that its source of energy is a water displacement event.

The wave speeds for tsunamis are very high in deep water. The tsunami of December 26, 2004 travelled from near the island of Sumatra to the east coast of Africa in just over seven hours. It was initiated by an earthquake of magnitude 9 off the western coast of northern Sumatra.

The wave speed depends upon wavelength and the depth of the water for tsunamis at sea. As waves enter shallower water, their wavelength and wave speed diminishes, causing their amplitudes to greatly increase.

Tsunami waves are distinguished from ordinary ocean waves by their great length between wave crests, often exceeding 100 km in the deep ocean water, and by the time between these crests, ranging from 10 minutes to an hour. As they reach the shallow waters of the coast, the waves slow down and the water can pile up into a wall of destruction tens of meters or more in height. The effect can be amplified where a bay or harbour funnels the wave as it moves inland. Large tsunamis have been known to rise over 30 meters. Even a tsunami 3 - 6 meters high can be very destructive and cause many deaths and injuries.

Some tsunamis consist of a single crest while others develop a broad trough in advance of the main wave and a succession of smaller waves behind. It is the preceding trough, together with man's curiosity, that has been the cause of much loss of life. People attracted by the very low water as the tsunami approaches have gone out to walk on the newly exposed sea floor and have been drowned as the rising pulse flooded shoreward.

Depth of water (m) 10 50 200 2000 4000 7000

Velocity (km.h^-1 ) 40 80 160 500 700 950

Wavelength (km) 10 20 50 150 200 280

amazing numbers !!!

Doing Physics with Matlab

Download mscripts

Animation produced with wm_travelling.m

If you have any feedback, comments, suggestions or corrections please email:

Ian Cooper matlabvisualphysics@gmail.com