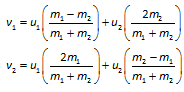DOING PHYSICS WITH MATLAB MECHANICS   SLINGSHOT EFFECT Ian Cooper mec_slingshot.m The mscript is used to create an animated gif of the slingshot effect where a spacecraft approaches a planet. The planet can be stationary or moving towards the spacecraft. The motion of the spacecraft is animated and changes in the kinetic energy and gravitational potential energy are displayed as well as plots of the speed of the spacecraft and its separation distance from the planet. A finite difference method is used to solve Newton’s Second Law for the gravitational attraction between the spacecraft and planet. From the solution you can calculate the trajectory of the spacecraft, its velocity, kinetic energy, potential and total energies of the system as functions of time. SLINGSHOT  EFFECT The slingshot effect is also known as a planetary swing-by or a gravity-assist manoeuvre. It is performed to achieve an increase in speed and/or a change of direction of a spacecraft as it passes close to a planet. As it approaches, the spacecraft is caught by the gravitational field of the planet, and swings around it. The speed acquired is then sufficient to throw the spacecraft back out again, away from the planet. By controlling the approach, the outcome of the manoeuvre can be manipulated and the spacecraft can acquire some of the planet’s velocity, relative to the Sun. The manoeuvre can be analysed as an elastic mechanical interaction, in which both momentum and kinetic energy are conserved. As a result of the interaction, the spacecraft will have sped up relative to the Sun, acquiring kinetic energy. The planet will have slowed very marginally, losing an equivalent amount of kinetic energy. Remember that EK = ½ m v^2 and the mass of a planet is very large so that the change in velocity of the planet is insignificant. The slingshot effect uses the motion of a planet to alter the path and speed of a spacecraft to manoeuvre it to travel to the outer planets of our solar system, which would otherwise be prohibitively expensive, if not impossible, to reach with current technologies. Consider a spacecraft on a trajectory that will take it close to a planet, say Jupiter. As the spacecraft approaches Jupiter which must be moving toward towards the spacecraft relative to the Sun for the slingshot effect to work - Jupiter's gravity pulls on the spacecraft, speeding it up. After passing the planet, the gravity will continue pulling on the spacecraft, slowing it down, but since Jupiter is moving, momentum and kinetic energy are transferred to the spacecraft. While the speed of the spacecraft has remained the same as measured with reference to Jupiter, the initial and final speeds may be quite different as measured in the Sun's frame of reference. Depending on the direction of the outbound leg of the trajectory, the spacecraft can gain a significant fraction of the orbital speed of the planet. In the case of Jupiter, this is over 13 km.s^-1. A spacecraft can gain kinetic energy (increase its speed) through an elastic collision with a moving planet as shown in the animation (figure 1).           Fig. 1.    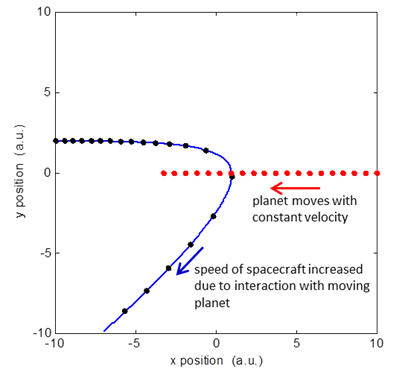Animation of the collision between a spacecraft (black) and a planet (red).  Figure 2 shows the trajectories of a spacecraft and a moving planet. The positions of the spacecraft and planet are shown at equal time intervals. The spacing between the positions is proportional to their velocities.           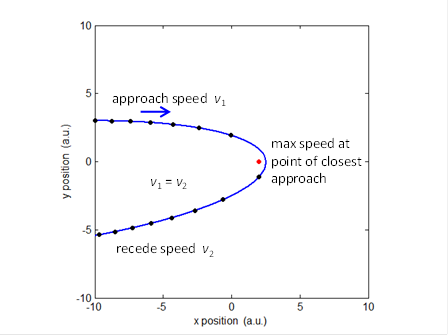Fig.2   The trajectory of a spacecraft during its interaction with a moving planet. The planet is much more massive than the spacecraft so in the elastic collision between them, the loss in momentum of the planet and its kinetic energy are insignificant. The total energy (E = EP + EK) of the spacecraft - planet system is constant. As the spacecraft approaches closer to the planet its gravitational potential energy must decrease and hence, its kinetic energy must increase (figure 3).           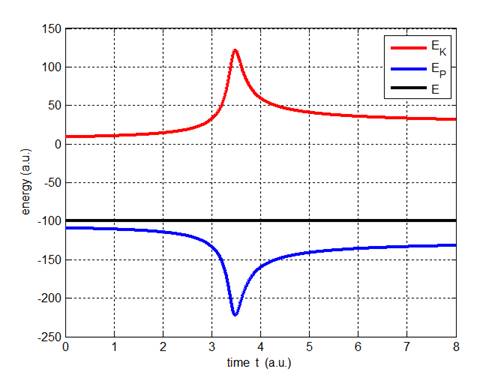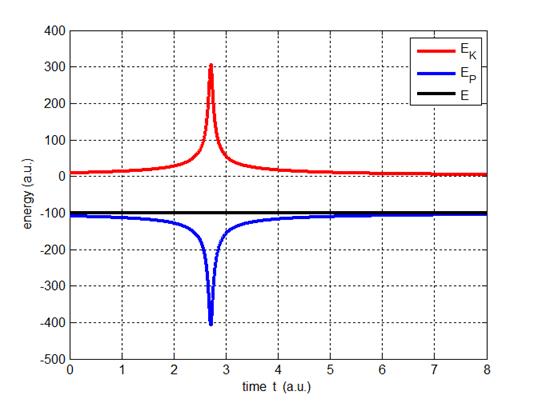Fig. 3.   The total energy of the system remains constant. As the spacecraft approaches the planet its kinetic energy           increases while the gravitational potential energy decreases and the kinetic energy decreases and gravitational potential energy increases as the spacecraft moves away from the planet. Therefore, the spacecraft will have its maximum speed when the distance between the spacecraft and planet is a minimum. Initially the planet and spacecraft are approaching each other and during the collision momentum is conserved, but, there is a net transferred of momentum from the planet to the spacecraft so that the speed at which the spacecraft recedes from the planet is greater than the speed at which it approached (figure 4).           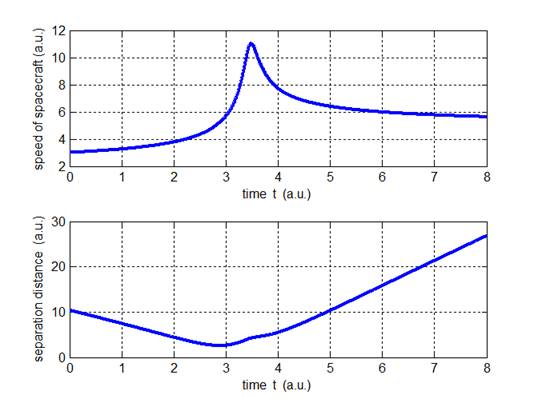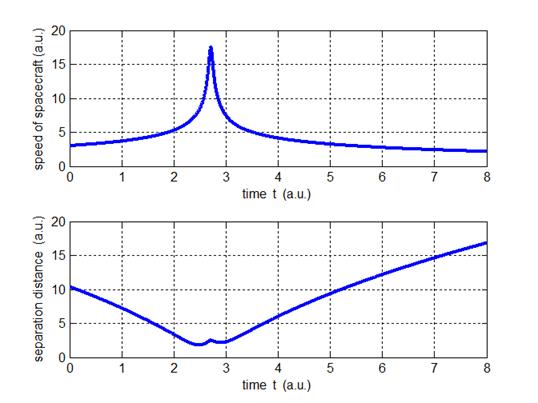Fig. 4.   The speed of the spacecraft changes as it sweeps past the moving planet.           The maximum speed of the spacecraft occurs at the minimum separation distance. If the planet was not moving then the approach and recede speeds are the same as shown in the animation (figure 5).             Fig. 5.   Animation of the collision between a spacecraft (black) and a stationary planet (red).           Figure 6 shows the trajectories of a spacecraft and a stationary planet. The positions of the spacecraft and planet are shown at equal time intervals. The spacing between the positions is proportional to their velocities.           Fig. 6.   The trajectory of a spacecraft during its interaction with a stationary planet. The planet is much more massive than the spacecraft so in the elastic collision between them, the loss in momentum of the planet and its kinetic energy are insignificant. The total energy (E = EP + EK) of the spacecraft - planet system is constant. As the spacecraft approaches closer to the planet its gravitational potential energy must decrease and hence, its kinetic energy must increase (figure 7). Since the planet is stationary, there is zero transfer of momentum or energy to the spacecraft, the approach speed and the speed of recession spacecraft are the same.          Fig. 7.   The total energy of the system remains constant. As the spacecraft approaches the planet its kinetic energy         increases while the gravitational potential energy decreases and the kinetic energy decreases and gravitational potential energy increases as the spacecraft moves away from the planet (figure 8).           Fig. 8.   The speed of the spacecraft changes as it sweeps past the stationary planet.          The maximum speed of the spacecraft occurs at the minimum separation distance.          The approach speed and receding speed are the same. Consider a one dimensional head-on elastic collision between two objects with masses m1 and m2. The initial velocities are u1 and u2 and the final velocities are v1 and v2. In the collision both momentum and kinetic energy are conserved and it can be shown that      (1)                Collision with a stationary target (m2): m1= 1 kg   m2 = 1000 kg   u1 = +10 m.s^-1 u2 = 0 m.s^-1 v1 = - 9.98 m.s^-1 v2 = + 0.02 m.s^-1      Initial KE (m1) = 50 J     Initial KE (m2) = 0 J     Total initial KE = 50 J      Final KE (m1)  = 50 J      Final KE (m2)  = 0 J     Total final KE   = 50 J The speed of the incident particle (m1) is smaller after the collision as some momentum and energy is transferred to the target particle (m2) during the elastic collision. Collision with a moving target (m2): m1= 1 kg   m2 = 1000 kg   u1 = +10 m.s^-1 u2 = - 10 m.s^-1 v1 = - 29.96 m.s^-1 v2 = - 9.96 m.s^-1      Initial KE (m1) = 50 J     Initial KE (m2) = 50 000 J     Total initial KE = 50 050 J      Final KE (m1)  = 449 J   Final KE (m2)   =  49 601 J     Total final KE   = 50 050 J The speed of the incident particle (m1) is significantly larger after the collision (increased by factor 3) and has a much larger final kinetic energy (increased by factor 9). Since m1 << m2 the speed and kinetic energy are much the same for the target particle (m2). We can now consider the case when m2 >> m1 In equation (1) divide the denominator and numerator by m2      (2)              2 represents the planet and 1 the spacecraft. Let u1 > 0 then u2 < 0 and since m2 >> m1  then  Equation (2) becomes      (3)             Equation (3) tells us that the spacecraft reverses direction and its speed increases whilst the velocity of the planet is unchanged. This is the reasoning behind why the slingshot effect is used to increases its speed and kinetic energy when passing a moving planet.