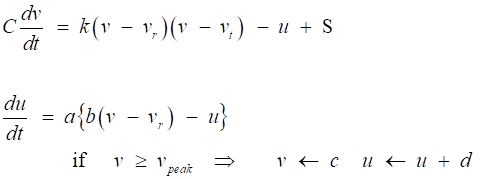DOING PHYSICS WITH MATLAB IZHIKEVICH QUADRATIC MODEL FOR SPIKING NEURONS
Matlab Download Directory ns_Izh_006.m Computation of the firing patterns of a single neuron using the Izhikevich Quadratic Model
This article and the Scripts are based upon the papers and book by E. M. Izhikevich Which Model to Use for Cortical Spiking Neurons? IEEE Transactions on Neural Networks. Vol. 15. No. 5. September 2004. Simple Models of Neural Networks IEEE Transactions on Neural Networks. Vol. 14. No. 6. November 2003. Hydrid Spiking Models Phil. Trans. R. Soc. A (2010) 368, 5061–5070 Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. The MIT Press. Izhiekvich’s website
The model of a neuron described in the book, Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting by Izhikevich is not based upon biophysical parameters but is a simple model that faithfully reproduces all the neurocomputational dynamical features of the neuron. The model is a two-dimensional systems having a fast voltage variable v and a slower “recovery” variable u, which may describe activation of the K^+ current or inactivation of the Na^+ current or their combination. The simple model to reproduce spiking and bursting behavior of many known types of neurons is described by the pair of differential equations (1)
Model parameters and dimensions: t time [ms] C membrane capacitance [pF = pA.ms.mV^-1] v membrane potential [mV] rate of change of membrane potential [mV.ms^-1 = V.s^-1] capacitor current [pA] vr resting membrane potential [mV] vt instantaneous threshold potential [mV] k constant (“1/R”) [pA.mV^-1 (10^-9 Ω^-1)] u recovery variable [pA] S stimulus (synaptic: excitatory or inhibitory, external, noise) [pA] rate of change of recovery variable [pA.ms^-1] a recovery time constant [ms^-1] b constant (“1/R”) [pA.mV^-1 (10^-9 Ω^-1) ] c potential reset value [mV] d outward minus inward currents activated during the spike and affecting the after-spike behavior [pA] vpeak spike cutoff value [mV]
The sum of all slow currents that modulate the spike generation mechanism is combined in the phenomenological recovery variable u with outward currents taken with the plus sign. The sign of b determines whether u is an amplifying (b < 0) or a resonant (b > 0) variable. In the latter case (b > 0) the neuron sags in response to hyperpolarized pulses of current, peaks in response to depolarized subthreshold pulses, and produces rebound (postinhibitory) responses. The parameters c and d do not affect steady-state subthreshold behavior. Instead, they take into account the action of high-threshold voltage-gated currents activated during the spike, and affect only the after-spike transient behavior. One difficulty in applying the Izhikevich model is the determination of the numerical values of the parameters to be used in stimulations of the time evolution of the membrane potential for different stimuli. The following simulations show how the model can be applied to three types of neurons.
1. Modelling Regular Spiking (RS) Neurons Regular spiking neurons are the major class of excitatory neurons in the neocortex (part of the cortex of the brain made up of six layers, labelled from the outermost inwards, I to VI). In humans, the neocortex is involved in functions such as sensory perception, generation of motor commands, spatial reasoning and language. RS neurons have a transient K^+ current IA whose slow inactivation delays the onset of the first spike and increases the interspike period, and a persistent K^+ current IM which is believed to be responsible for the spike frequency adaptation. Regular spiking neurons fire tonic spikes with adapting (decreasing) frequency in response to injected pulses of DC current. Most of them have Class 1 excitability in the sense that the interspike frequency vanishes when the amplitude of the injected current decreases. These neurons are spiny stellate cells in layer 4 and pyramidal cells in layers 2, 3, 5, and 6. The simulated voltage responses of the model agree quantitatively with the in vitro recordings of the layer 5 pyramidal neuron. Model parameters for RS neurons in the neocortex: Membrane resting membrane vr = −60 mV Instantaneous threshold potential vt = −40 mV (instantaneous depolarizations above −40 mV cause the neuron to fire) The minimal amplitude of injected current of infinite duration needed to fire a neuron is called the rheobase The parameters k and b can be found when one knows the neuron’s rheobase and input resistance rheobase = 50 pA Input resistance R = 80 MΩ Þ k = 0.7 and b = −2. how ? Membrane capacitance C = 100 pF Þ membrane time constant t = R C = 8 ms When b < 0, the depolarizations of v decrease u as if the major slow current is the inactivating K^+ current IA The inactivation time constant of IA is around 30 ms in the subthreshold voltage range Þ a ≈ 1/30 ≈ 0.03 The membrane potential of a typical RS neuron reaches the peak value vpeak = +35 mV during a spike and then repolarizes to c = −50 mV or below, depending on the firing frequency The parameter d describes the total amount of outward minus inward currents activated during the spike and affecting the after-spike behavior d = 100 gives a reasonable f-I (or f-S) relationship in the low-frequency range. All the figures 1… were created using the Matlab mscript ns_Izh_006.m. with the parameters: C = 100; vr = -60; vt = -40; k = 0.7; % parameters used for RS a = 0.03; b = -2; c = -50; d = 100; % neocortical pyramidal neurons vPeak = 35; % spike cutoff [mV] dt = 0.5; % time step [ms]
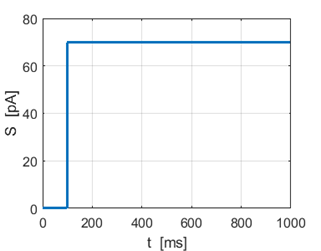
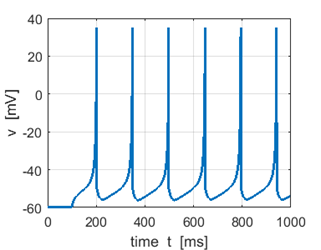
Fig. 1A. Input stimulus Sstep = 70 pA.				Fig. 1B. Membrane potential.
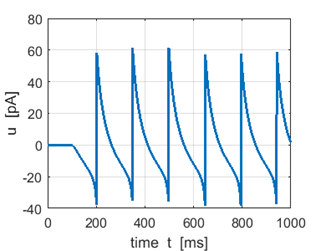
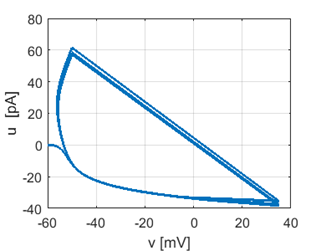
Fig.1C. Recovery variable.				Fig. 1D. Phase plot.
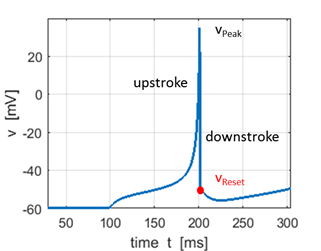
Fig.1E. Expanded view of a spike. The shape of the action potential is very similar to the recording of actual neocortical pyramidal neurons but with two discrepancies: recording has a sharper spike upstroke and a smoother spike downstroke. The simple model generates the upstroke of the spike due to the intrinsic (regenerative) properties of the voltage equation. The voltage reset occurs not at the threshold, but at the peak, of the spike. The firing threshold in the simple model is not a parameter, but a property of the bifurcation mechanism of excitability. Depending on the bifurcation of equilibrium, the model may not even have a well-defined threshold, a situation similar to many conductance-based models. Pyramidal neurons (pyramidal cells) are a type of neuron found in areas of the brain including the cerebral cortex, the hippocampus, and the amygdala. Pyramidal neurons are the primary excitation units of the mammalian prefrontal cortex and the corticospinal tract. Key features: triangular shaped soma (after which the neuron is named), a single axon, a large apical dendrite, multiple basal dendrites, and the presence of dendritic spines.				Resting membrane potential vr = −60 mV Instantaneous threshold potential vt = −40 mV Instantaneous depolarizations above −40 mV cause the neuron to fire The slow afterhyperpolarization (AHP) following the reset that is due to the dynamics of the recovery variable u.
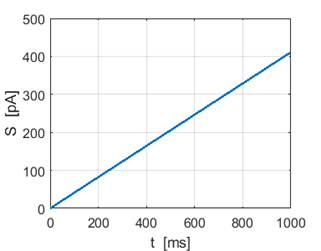
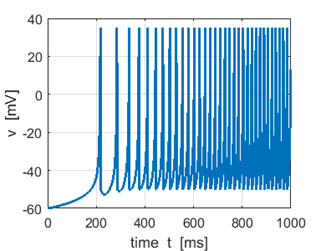
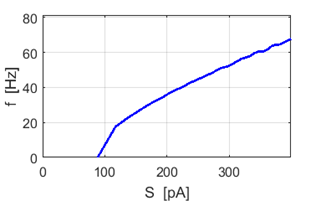
Fig. 1F. Ramp stimulus.		Fig. 1G. Membrane potential: spike frequency increases as stimulus strength S increases.			Fig. 1H. f-S curve showing how the spike frequency increases with increasing stimulus strength.
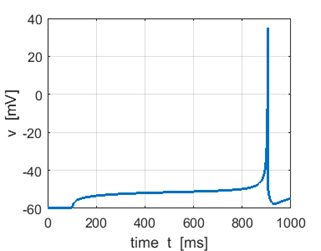
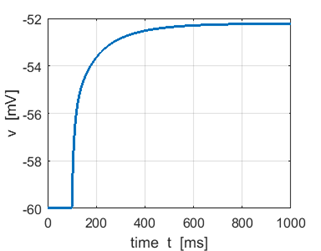
Fig. 1I. Step input Sstep = 52 pA produces a spike, but no spike is generated for Sstep = 51 pA.				Fig. 1J. Step input Sstep = 51 pA. The minimal amplitude of the injected current of infinite duration needed to fire a neuron is called the rheobase.
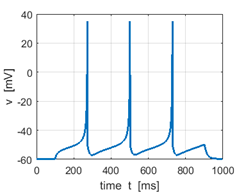
Fig. 1K. Step input stimulus Sstep = 60 pA	Sstep = 60 pA Mean firing rate f = 4.4 Hz			Sstep = 80 pA f = 8.9 Hz		Sstep = 100 pA f = 13.1 Hz Increasing the input stimulus strength increases the firing rate
2. Modelling Intrinsically Bursting (IB) Neurons
Intrinsically bursting (IB) neurons generate a burst of spikes at the beginning of a strong depolarizing pulse of current, then switch to tonic spiking mode. They are excitatory pyramidal neurons found in all cortical layers, but are most abundant in layer 5. Some IB neurons respond to the injected pulses of DC current with a burst of high-frequency spikes followed by low-frequency tonic spiking. Many IB neurons burst even when the current is barely superthreshold and not strong enough to elicit a sustained response. However, other IB neurons give a bursting response only to strong current stimuli and weaker stimulation elicits a regular spiking response. In comparison with typical RS neurons, the regular spiking response of IB neurons have a lower firing frequency and higher rheobase (threshold) current, and exhibits shorter latency to the first spike and noticeable afterdepolarizations. The initial high-frequency spiking is caused by the excess of the inward current or the deficit of the outward current needed to repolarize the membrane potential below the threshold. As a result, many spikes are needed to build up outward current to terminate the high-frequency burst. After the neuron recovers, it fires low-frequency tonic spikes because there is a residual outward current (or residual inactivation of inward current) that prevents the occurrence of another burst. Many IB neurons can fire two or more bursts before they switch into tonic spiking mode. Default model parameters for IB neurons for a step input as in figure 1K: C = 150 vr = -75 vt = -45 k = 1.2 a = 0.01 b = 5 c = -56 d = 130 vPeak = 50 Rheobase = 350 pA input resistance ~ 30 MΩ
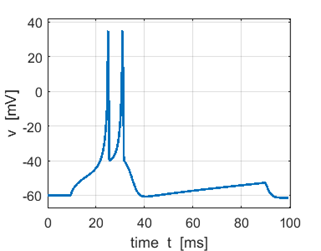
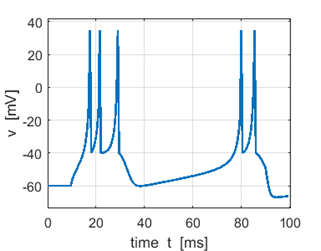
Fig. 2A. Sstep = 300 pA. The input current is less than the rheobase, therefore, the neuron does not fire.				Fig. 2B. Sstep = 400 pA Low frequency tonic spiking with adaptation since the input stimulus is only slightly greater than the rheobase value.
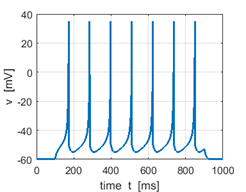
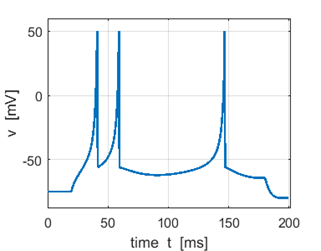
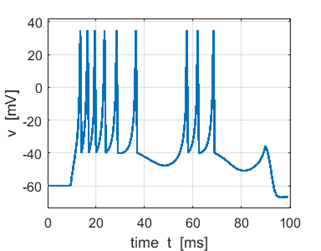
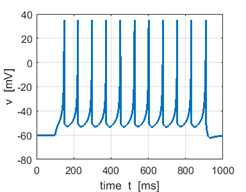
Fig. 2C. Sstep = 500 pA. The first spike is a doublet.				Fig. 2D. Sstep = 600 pA. the first spike is a triplet.
3. Modelling Chattering (CH) Neurons
Chattering (CH) or fast rhythmic bursting (FRB) neurons generate high-frequency repetitive bursts in response to injected depolarizing currents. The magnitude of the DC current determines the interburst period, which could be as long as 100 ms or as short as 15 ms and the number of spikes within each burst is typically from two to five. CH neurons are found in visual cortex of adult cats, and morphologically they are spiny stellate or pyramidal neurons of layers 2 - 4, mainly layer 3. Default model parameters for IB neurons for a step input as in figure 1K: C = 50 vr = -60 vt = -40 k = 1.5 a = 0.03 b = 1 c = -40 d = 150 vPeak = 35 The results of the simulations are shown in figures 3…. The plots are very similar to vivo recordings from cat primary visual cortex.
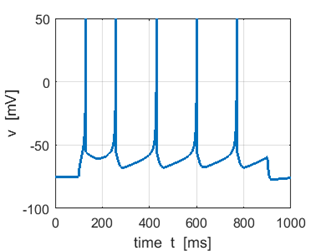
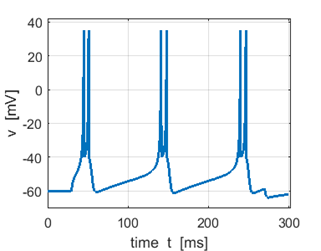
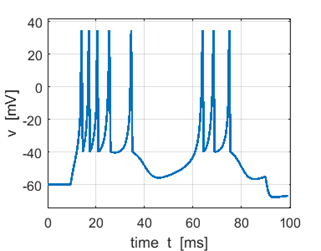
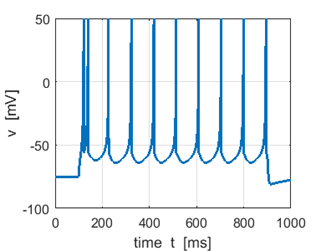
Fig. 3A. Sstep = 200 pA. Doublet spikes.				Fig. 3B. Sstep = 300 pA. Triplet first spike.
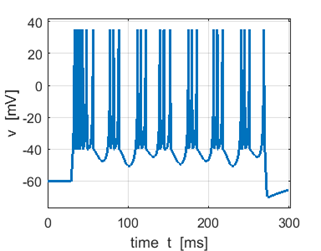
Fig. 3A. Sstep = 500 pA. Multiple spikes.				Fig. 3A. Sstep = 600 pA. Multiple spikes.
The model described by equation 1 can quantitatively reproduces subthreshold, spiking, and bursting activity of all known types of cortical and thalamic neurons in response to pulses of DC current. The simple model makes testable hypotheses on the dynamic mechanisms of excitability in these neurons and the model is especially suitable for simulations of large-scale models of the brain.