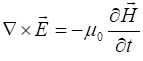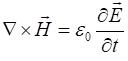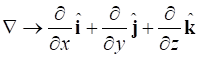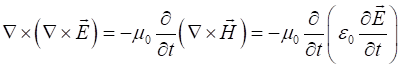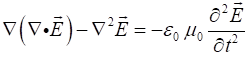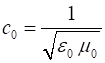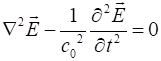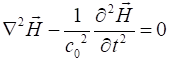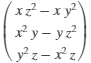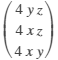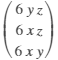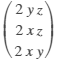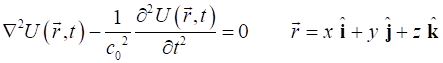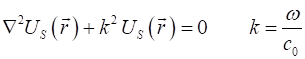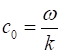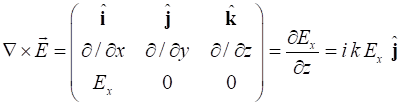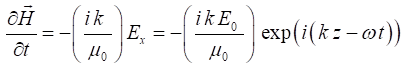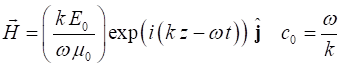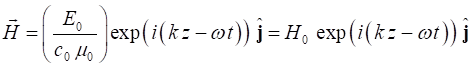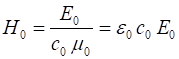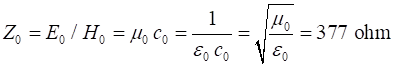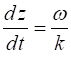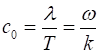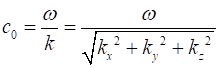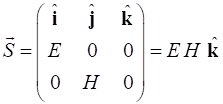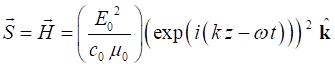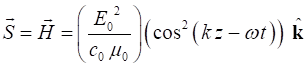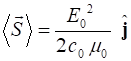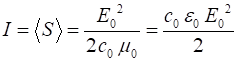DOING PHYSICS WITH MATLAB

NUMERICAL ANALYSIS OF OPTCIAL AND ELECTROMAGNETIC PHENOMENA

PROPAGATION OF ELECTROMAGNETIC WAVES IN FREE SPACE

Ian Cooper

matlabvisualphysics@gmail.com

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

op_001.m

Plots and an animation of a plane wave propagating in the +Z direction. The wavelength of the EM wave is changed in the INPUT section of the script and should be in the range for visible light (380 nm to 780 nm). The plots are color coded to match the color of the light by calling the script colorCode.m.

op_002.m

[2D] animation of a plane wave propagating in +Z direction.

opLE1001.mlx

LIVE EDITOR: Vector calculus applied to plane EM waves using the Symbolic Toolbox.

THE WAVE EQUATION IN FREE SPACE

Electromagnetism is the fundamental theory that underlies most of optics associated with wave phenomena. Maxwell’s equations provide the basic information needed to describe electromagnetic phenomena. Equation 1 gives a summary of Maxwell’s equation for free space (vacuum).

(1A) Gauss’s Law

(1B)

(1C) Faraday’s law

(1D) Ampere’s Law

electric field [V.m^-1]

magnetic field [T]

= 8.85x10^-12 F.m^-1 electric permittivity of free space

= 4x10^-7 N.A^-2 magnetic permeability of free space

We can use Maxwell’s equation to derive the wave equation using the identify for the vector

(2)

The speed of light in free space is

(3)

The speed of light in free space is defined to be

So, the wave equations for the electric and magnetic fields are

(4A)

(4B)

LIVE EDITOR opLE1001.mlx Vector Calculus

We can use the Live Editor in Matlab to symbolically evaluate various calculus operators. Consider the vector field . We can calculate the curl, the divergence and the vector Laplacian of the vector field given by . Note: the Laplacian of the vector field is calculated using the identify given in equation 2.

syms x y z

% Vector field

A = [x^2*y*z, y^2*z*x, z^2*x*y]

% Cartesain system

vars = [x y z]

% Curl

R1 = curl(A,vars)

R2 = curl(R1,vars)

% Divergence

R3 = divergence(A,vars)

% Gradient

R4 = gradient(R3)

% Laplacian

R = R4 - R2

R1 = 

R2 = 

R3 = 

R4 = 

R = 

Using the symbolic functions in the Live Editor, you no longer need to do all the tedious algebra manipulations for many calculus operations.

PLANE HARMONIC (MONOCHROMATIC) WAVES

The vectors for the electric field and magnetic field can be resolved into their X, Y and Z Cartesian components and each component of and satisfies the scalar wave equation

(5)

where is called the wavefunction representing any one of the field components .

It is often convenient to assume that the wavefunction varies harmonically (sinusoidal variation with time), so the wavefunction can be expressed the product of a spatial wavefunction and a harmonic time-varying function

(6)

By substitution of equation 6 into equation 5, we can derive the Helmholtz equation

(7)

The Maxwell equations 1C and 1D, for harmonically varying fields, reduce to

(8C)

(8D)

We will consider the special case of a plane harmonic electromagnetic wave propagating in the +Z direction, where

(9)

Amplitude of the wave [V.m^-1]

Phase of the wave [rad]

Propagation constant or wave number [m^-1 or rad.m^-1]

Angular frequency [s^-1 or rad.s^-1]

By direct substitution of equation 9 into equation 5, it is to verify that the electric field given by equation 9 is a solution to the wave equation (5) provided that the ratio of the constants and is

(10)

We can then substitute equation 9 into the Maxwell equation 1C to find the magnetic field component of our plane harmonic electromagnetic wave

(11)

The ratio is called the impedance of free space (wave impedance of a plane wave)

Our plane harmonic electromagnetic wave is a transverse wave propagating in the +Z direction with the electric field varying in the +X direction and the magnetic field varying in the +Y direction. The vibrations of the electric field and the magnetic field are in phase at the same frequency at all times. This type of wave, in which the electric field vector is always parallel or antiparallel to a fixed direction is called a plane-polarized wave. 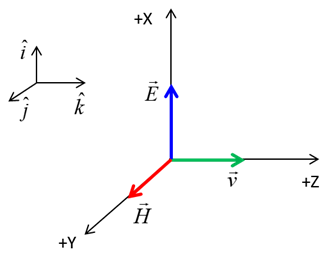For the solution given by equation 9, the plane of polarization is the XY plane (figure 1).

Fig. 1. A plane electromagnetic wave propagating in the +Z direction. The direction of propagation and the directions of the oscillations for the electric field and magnetic field are mutually orthogonal. The plane of polarization is the XY plane.

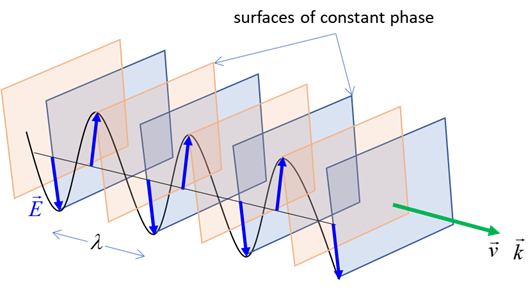
Fig. 2. Wavefronts of a plane wave travelling in [3D] space. The direction of propagation is perpendicular to the planes of constant phase.

The wave advances such that the phase in the plane perpendicular to the direction of propagation remains constant.

We can differentiate this expression for the phase with respect to time t

But is the velocity at which the phase advances. Therefore, the plane wave given propagates in the +Z direction with a phase velocity where

(10)

When the phase of the wave increases by rad (one complete cycle), the value of the electric field is unchanged

For one cycle, where the wave advances a distance and the electric field values at and are the same

(12)

is the wavelength and corresponds to the distance measured along the direction of propagation such that the electric field or magnetic field goes through one complete cycle. Hence, the propagation constant k is the spatial frequency and is the number of cycles in the distance.

For one cycle, where the time advances by T and the electric field values at times and are the same

(13)

T is the period and is the time for one complete oscillation. The reciprocal of the period T is the frequency f and is the number of cycles per unit time.

T period [s]

f frequency [Hz]

Hence, the wave travels a distance in the time interval T. The phase velocity of the wave is defined as

(10)

For a plane wave given by

the phase velocity is , hence the wave travels in the Z direction.

The solutions of electromagnetic field problems with an arbitrary time dependence can be constructed by using Fourier transformation theory.

LIVE EDITOR: Vector Calculus opLE1001.mlx

We can use the Live Editor to verify equation 9 is a solution of the scalar wave equation 6.

syms k z w t

clc

E = exp(-1i*(k*z - w*t))

v = w/k

% LHS = d2E_dtz2 RHS = (1/v^2)*d2E/dt2

LHS = diff(E,z,2)

RHS = (1/v^2)*diff(E,t,2)

E = 

v = 

LHS = 

RHS = 

Returning now to the [3D] wave equation (5), it is readily verified that equation (5) is satisfied by the three-dimensional plane harmonic wavefunction

(14)

where the position vector is

and the propagation vector is given by its components

Constant values of the phase define a set of planes in space called surfaces of constant phase (figure 2) where

and the propagation vector is normal to the surfaces of constant phase and the phase velocity is

(10)

The wavefunctions are expressed as complex function. However, it is only the real part of these functions that represent actual physical quantities.

ENERGY FLOW AND THE POYNTING VECTOR

The rate at which energy is transferred by a plane wave is given by the Poynting vector S [W.m^-2] which is defined as the cross produce of the electric and magnetic fields

(15)

For our harmonic wave

(9)

(11)

Taking the real part for the actual value of the Poynting vector

The average value of the cosine squared is equal to ½. Hence, the time average value of the Poynting vector is

The flow of energy is in the same direction in which the wave propagates.

The magnitude of the average Poynting vector is called the intensity or irradiance, so

(16)

Thus, the rate of energy flow is proportional to the square of the amplitude of the electric field.

The temporal and spatial variations of the electromagnetic field for a 1.0 mW plane monochromatic wave propagating in the +Z direction with its plane of polarization directed long the X-axis are displayed in figure 3, 4 and 5 for green light . A wavelength in the range from 380 nm to 780 nm can entered in the INPUT section of the script. The wavelength is assigned a color to match its spectral color by calling the function colorCode.m.

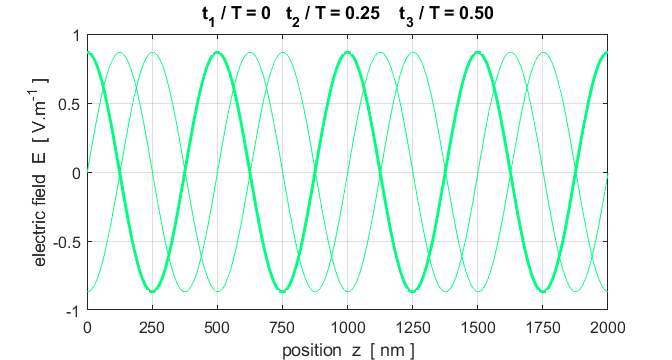
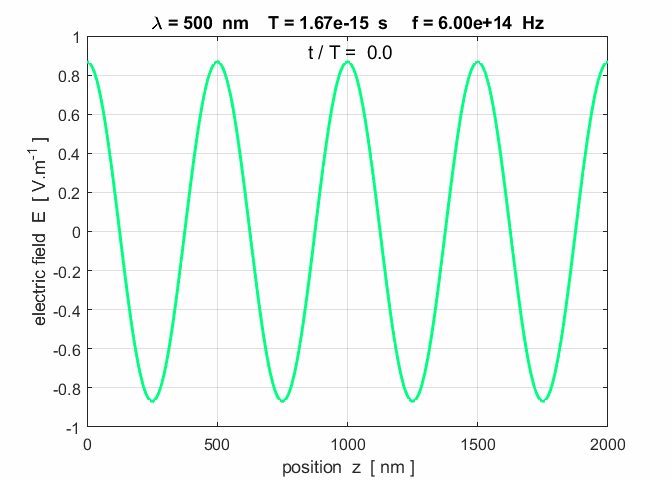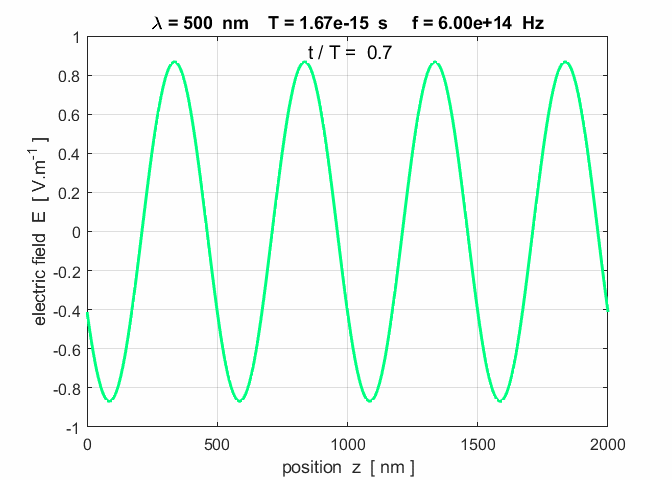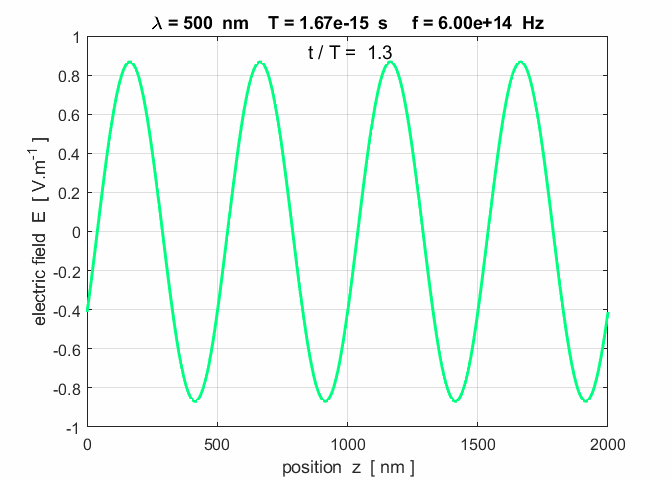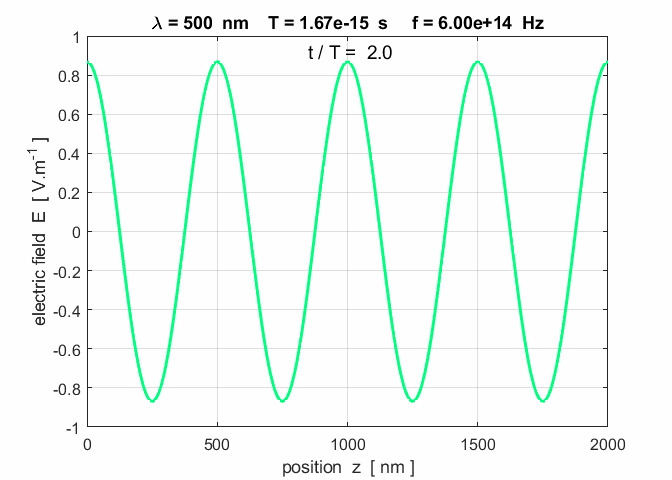
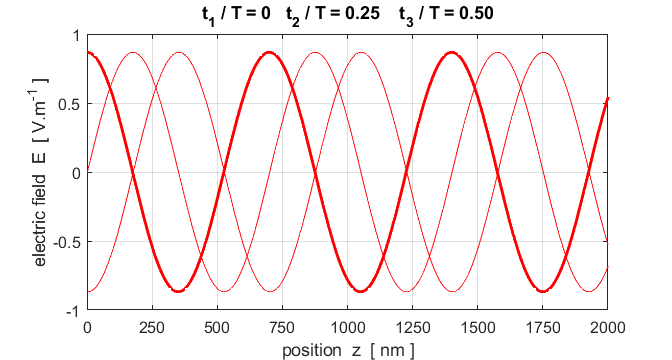
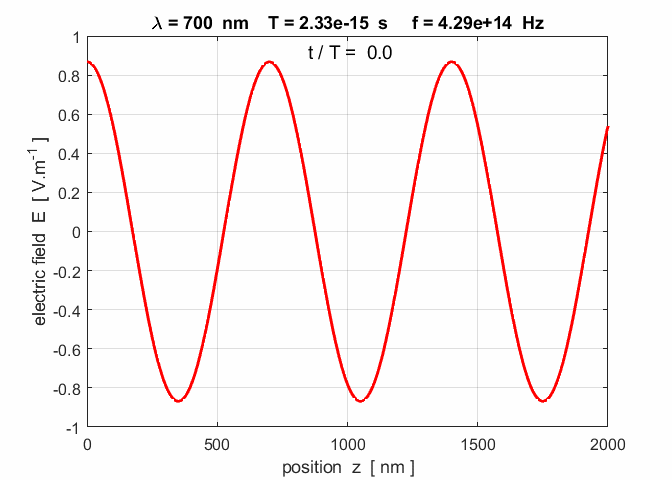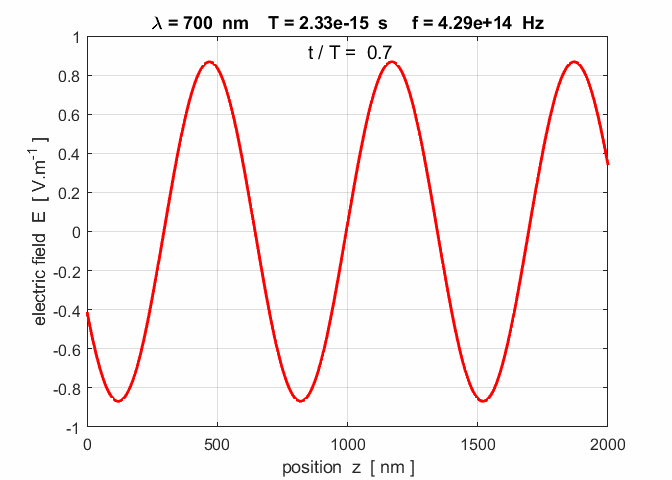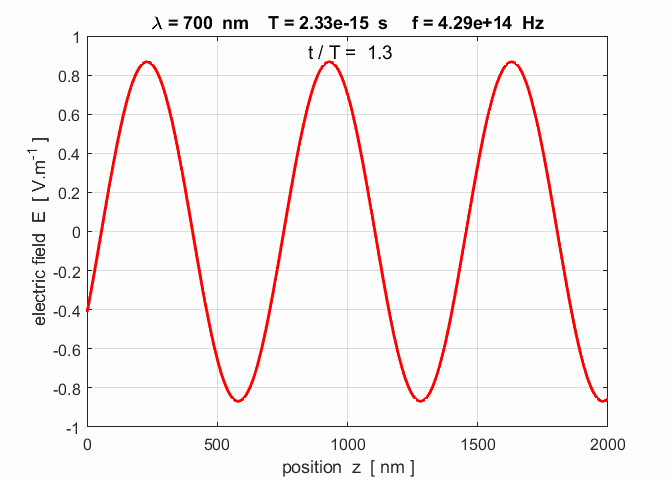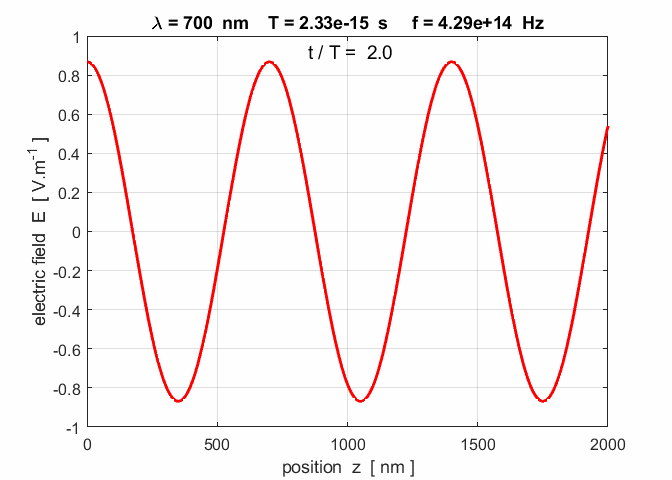
Fig. 3. A plot of the electric field as a function of position at three time steps. Note: the wave advances to the right a distance of one wavelength in a time interval of one period. op_001.m

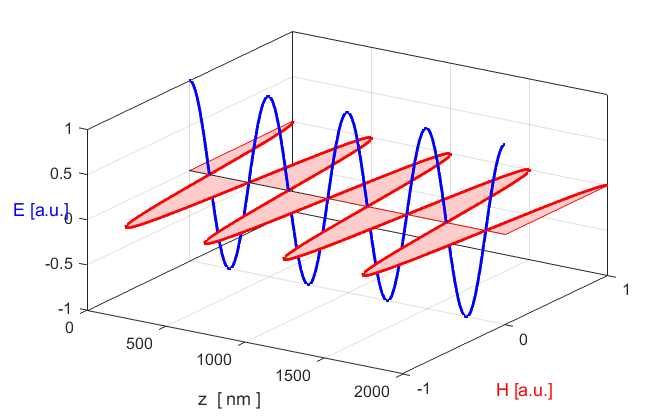
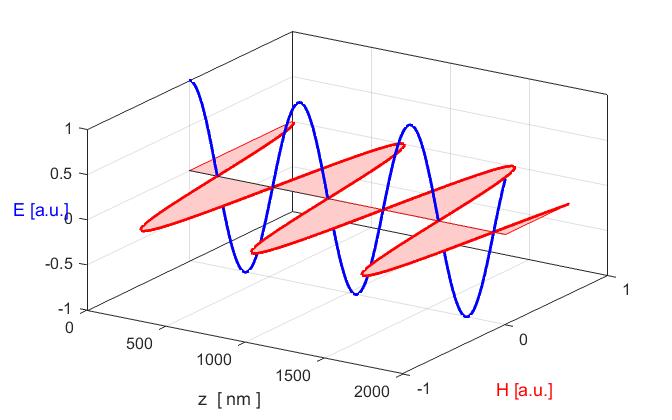
Fig. 4. The oscillations of the electric field and magnetic field are in phase and perpendicular to each other and perpendicular to the direction of propagation as shown in figure 1. op_001.m

Fig. 5. Animation of the vibration of the electric field as the wave propagates in the +Z direction. From the plot, you can verify the relationship . How far does the wave advance in one period? op_001.m

Figure 6 shows the electromagnetic fields for red light .

Fig. 6. The electromagnetic fields for a plane wave with . op_001.m

It is easy to create an animation of a plane wave propagating in two-dimensions. The [2D] version of a plane wave shows how the wavefronts are straight lines (lines of constant phase) that move in the direction of propagation. In [3D], you can think of the straight lines of constant phase as planes extending out of the screen and moving in the direction of propagation.

Fig. 7. [2D] view of a plane wave. op_002.m

Live Editor Poynting vector opLE1001.mlx

Calculation of the Poynting vector for a plane wave polarized in the X-direction.

syms k z w t E0 mu0 c0

E = [E0*exp(1i*(k*z - w*t)), 0, 0]

H = [0, E0/(c0*mu0)*exp(1i*(k*z - w*t)), 0]

S = cross(E,H)

E = 

H = 

S =