NUMERICAL ANALYSIS OF OPTICAL AND ELECTROMAGNETIC PHENOMENA

LINEAR POLARIZED LIGHT

MALUS’ LAW

Ian Cooper

matlabvisulaphysics@gmail.com

op_005.m

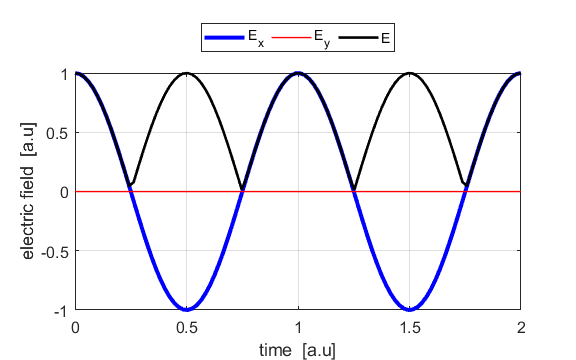
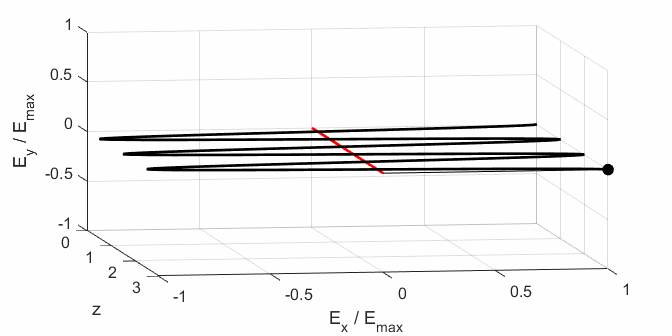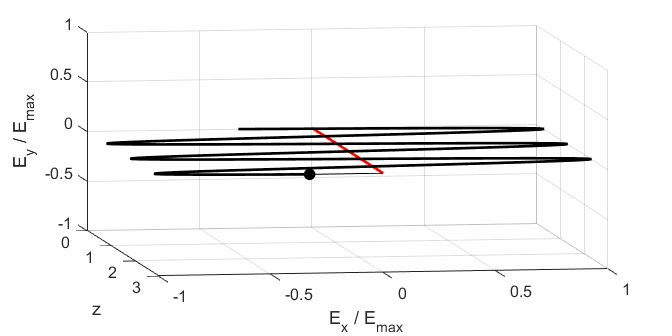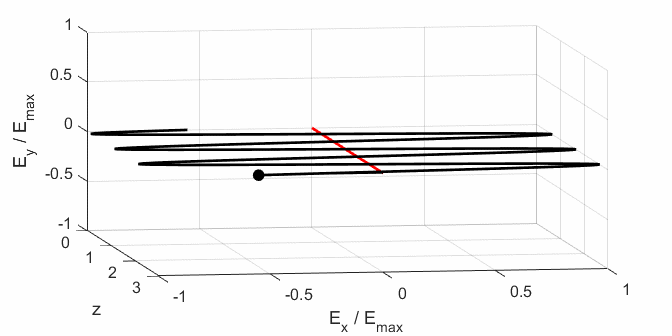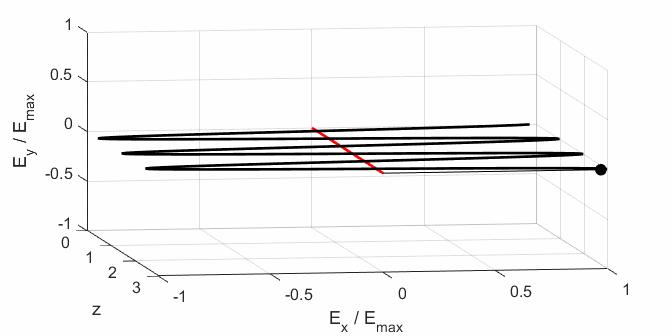
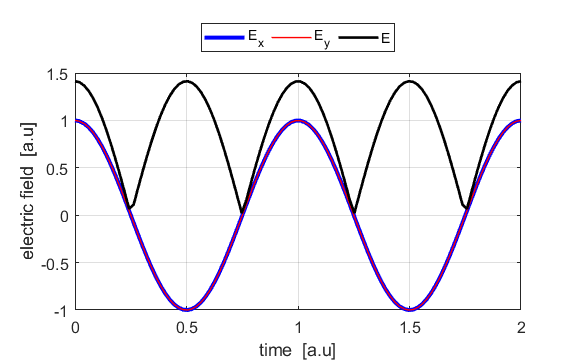
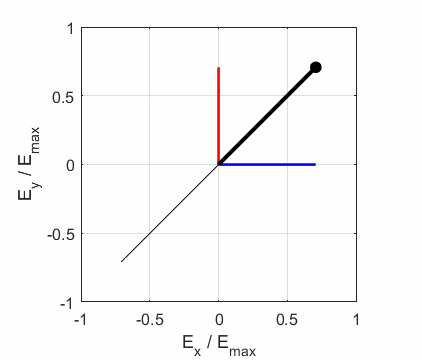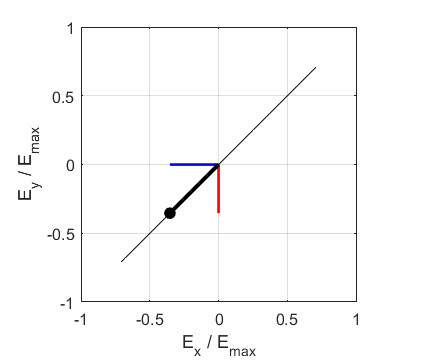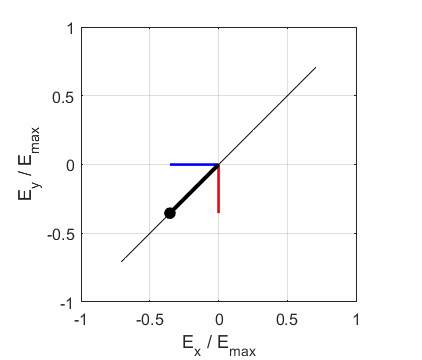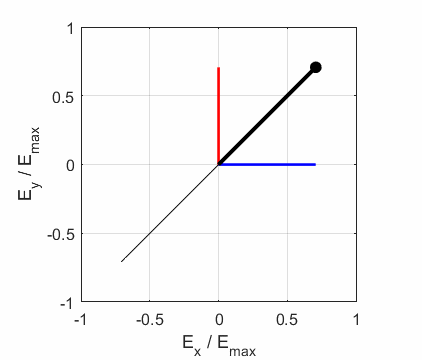
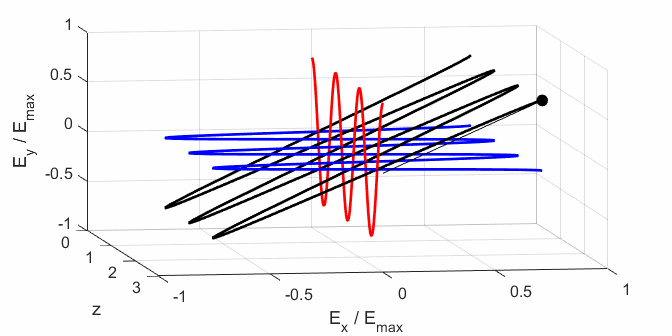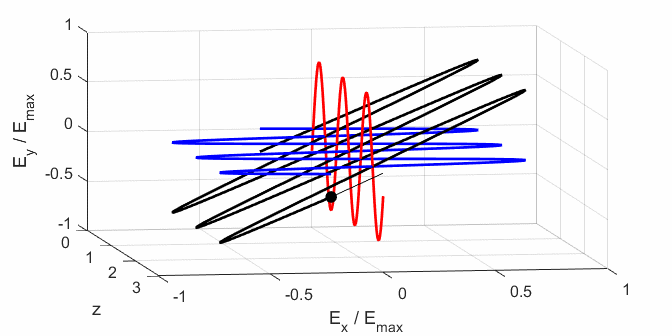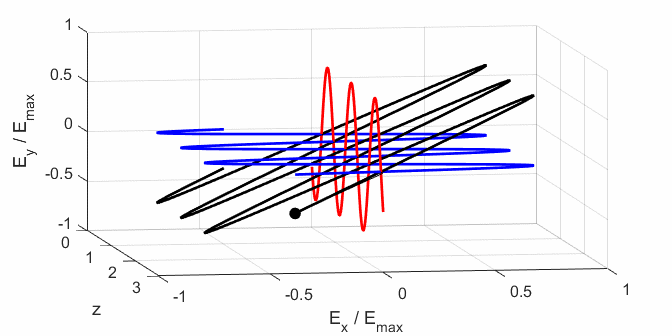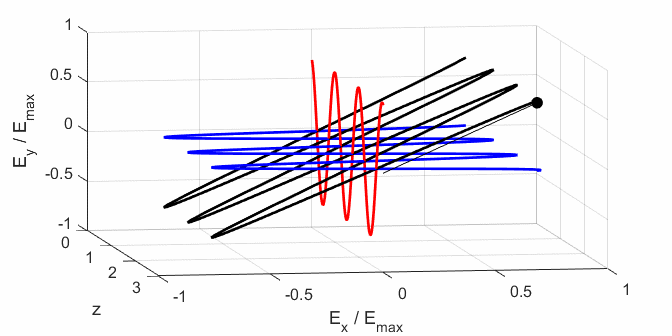
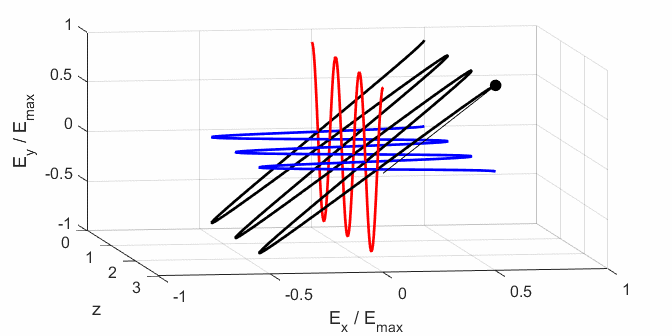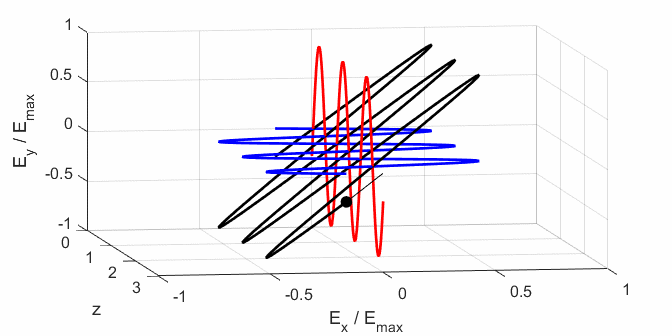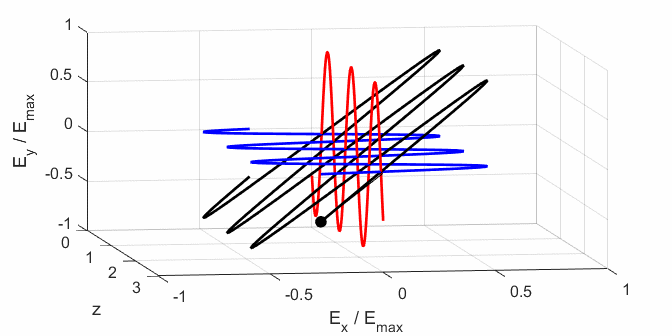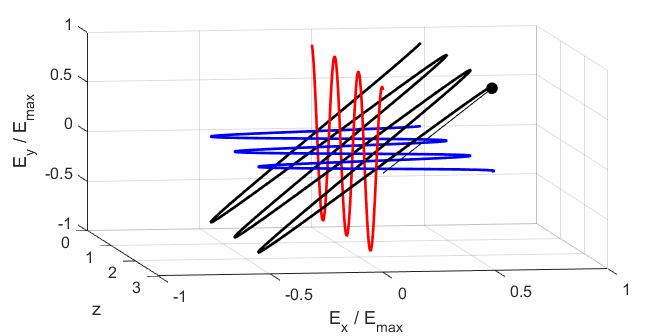
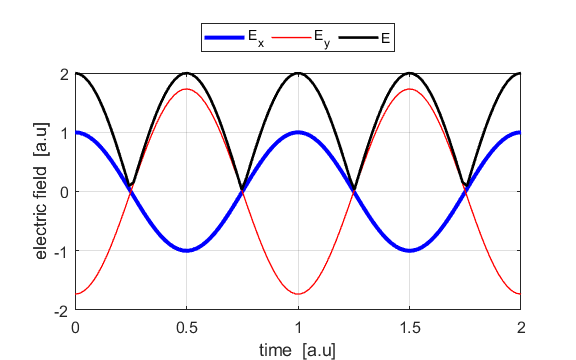
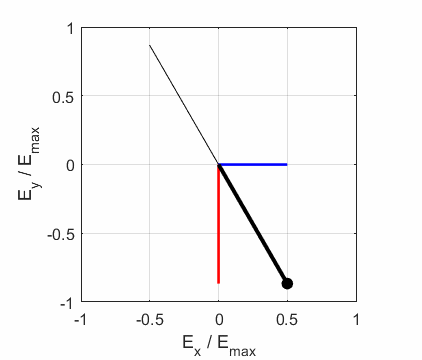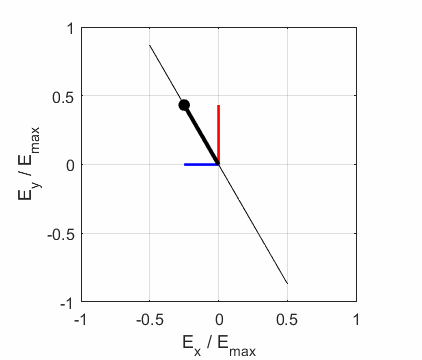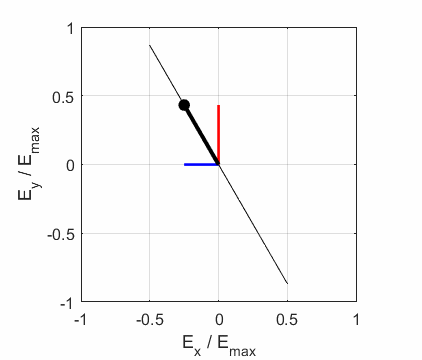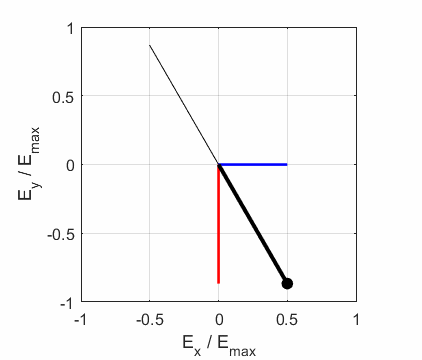
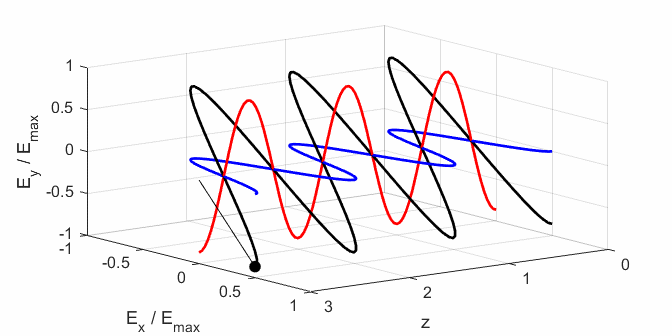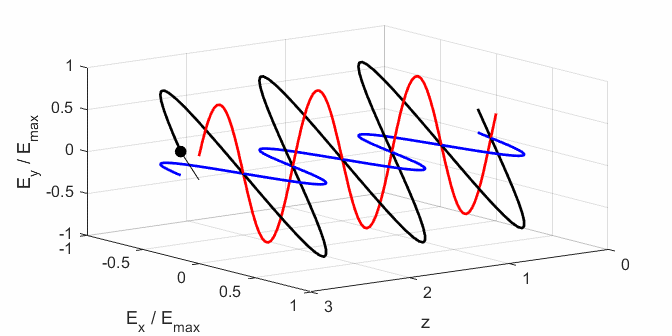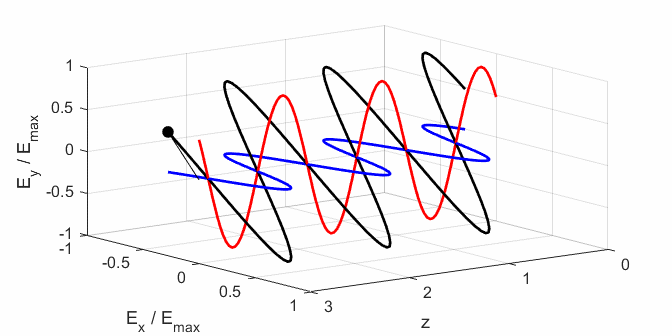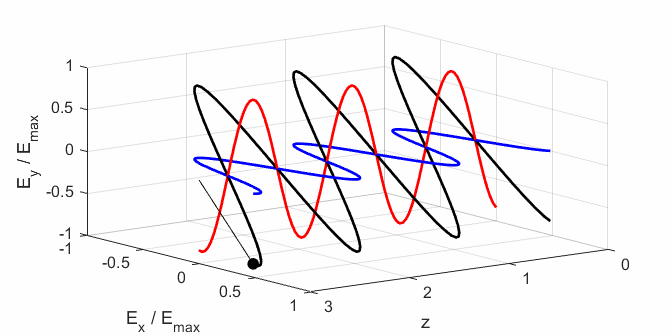
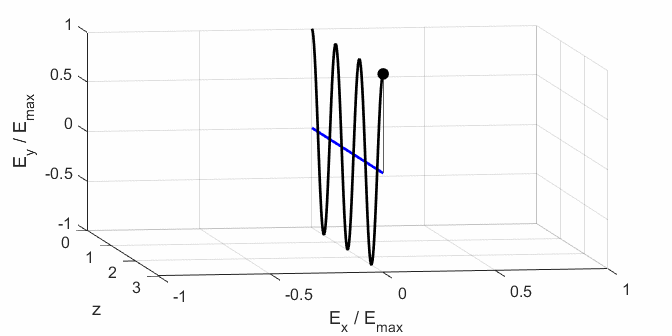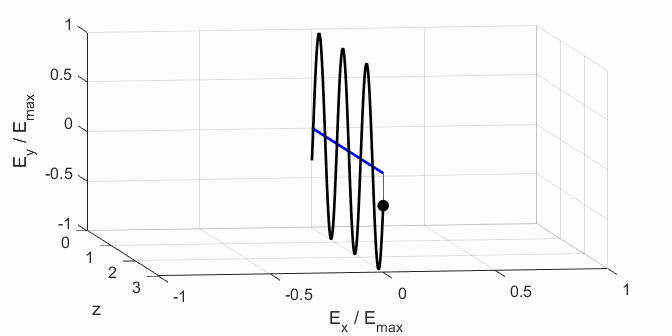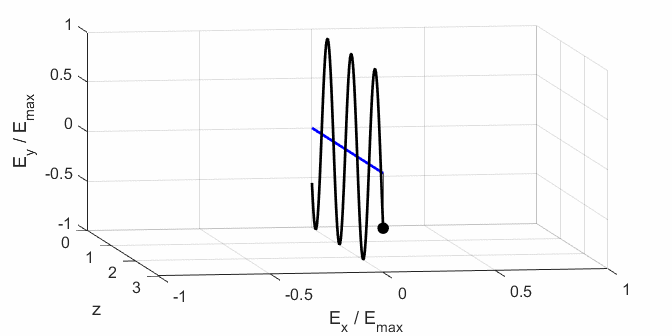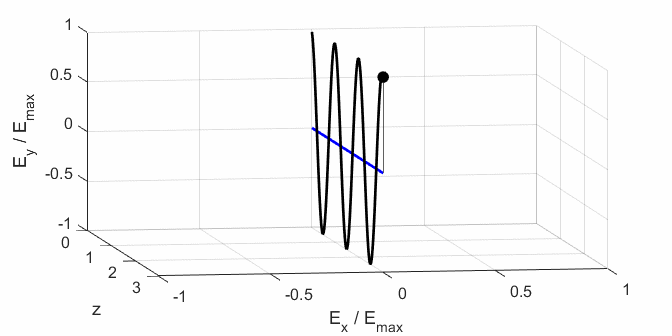
The Script op_005.m can be used to model the any type of polarization. The animations of the electric field vector can be saved as animated gif files (flag1 and flag2). In the INPUT SECTION of the Script, you can enter the amplitudes of the electric field components and their phase angles (flagP = 1) or the Jones parameters (flag2 = 2). From the input values, the electric field (E, Ex, Ey) as functions of time t and position z are calculated. 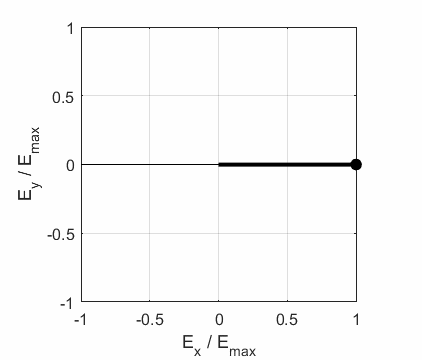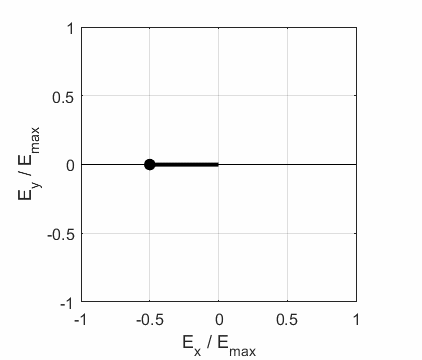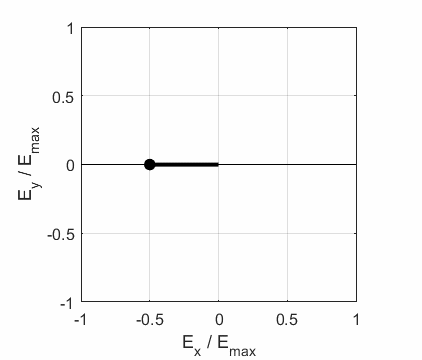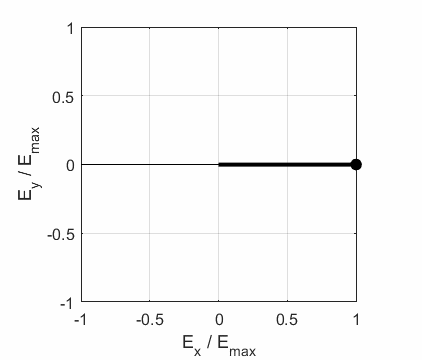In any plane (z = constant), the electric field vector sweeps out an ellipse with time (a straight line: linear polarization and a circle: circular polarization are special cases of an ellipse). The time evolution of the magnitude of the electric field is used to find its maximum Emax and minimum Emin values and the angle for the orientation of the major axis of the ellipse with respect to the X axis.

op_006.m

The Script is used to give an animation which illustrates Malus’ Law. Unpolarized light is passed through a polarizer to produce linear polarized light. The light then passes through an analyzer that rotates through an angle from 0^o to 180^o. So, the light emerging from the analyzer is and its irradiance is .

Background document: Mathematical foundations

Visual Physics Online: Polarization

1. Vertical Polarized Light

2. Horizontal Polarized Light

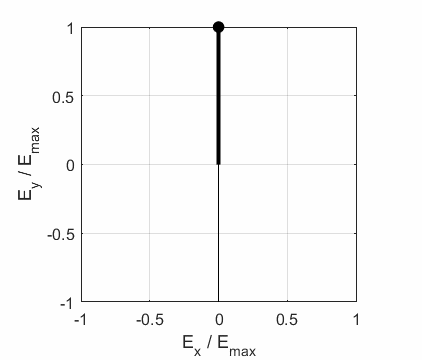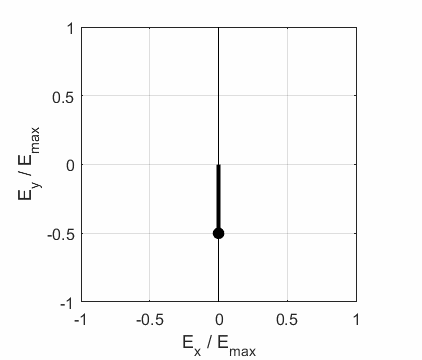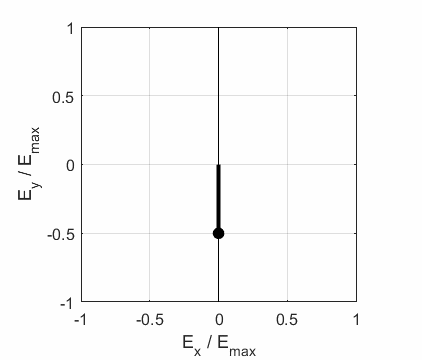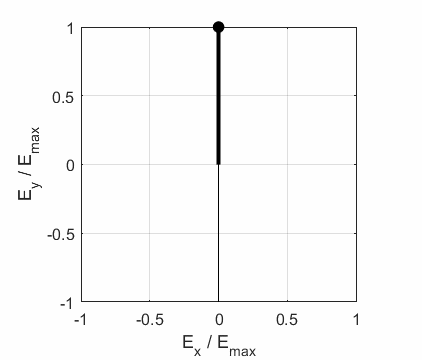
3. Linearly Polarized Light

4. Linear Polarized Light

5. Linearly Polarized Light

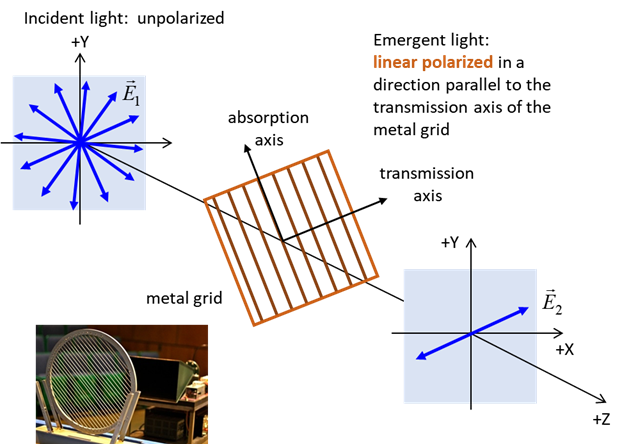
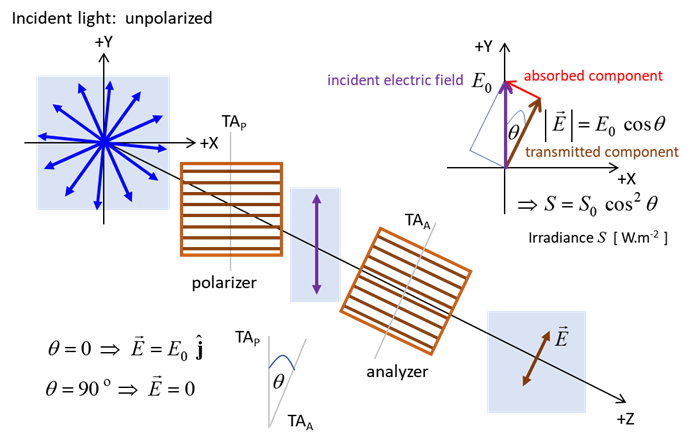
POLARIZATION BY SELECTIVE ABSORPTRION AND MALUS’ LAW

The absorption of light strongly along one direction and easily transmitted along a perpendicular direction is best understood by considering an experiment with microwaves as shown in figure 1.

Fig. 1. Action of a metal grid on an unpolarized microwave beam. All components of the electric field parallel to the metal grid are absorbed and all components perpendicular to the metal grid are transmitted provided >> grid spacing.

Provided that the wavelength of unpolarized microwave radiation is much larger than the metal grid spacing then the microwave radiation passing through the metal grid is linearly polarized in the direction which is perpendicular to the metal grid and zero radiation is emitted with an electric field component that is parallel to the metal grid. The explanation of this observation involves a consideration of the interaction of EM radiation with the metal wires. Within the metal wires, the mobile free electrons can oscillate at the frequency of the incident microwave radiation. These oscillating electrons acts a dipole source and emit radiation in all directions except in the direction of the oscillation. The transmitted wave is thus a superposition of the incident radiation and the radiation emitted by the oscillating electrons in the wires. However, in turns out that the two sources of radiation are 180^o out of phase and cancel each other for the component of the incident radiation which is parallel to the metal wires. So, if the metal grid is in a vertical position and the incident microwave radiation is vertically polarized, zero or very little radiation is propagated in the forward direction. Also, the oscillations of the electrons are not entirely free. The oscillating electrons constitute an electric current and energy is dissipated by the ohmic heating of the metal grid. But, the main reason for the disappearance of the emergent wave is the destructive interference between the incident wave and the generated wave. When the incident wave is horizontally polarized, then the maximum intensity of light is transmitted because appreciable oscillatory motion across each wire is inhibited.

Consider unpolarized microwave radiation incident upon a metal grid aligned in the horizontal direction (assume the polarizer is ideal). Then, only the vertical components are transmitted whereas the horizontal components absorbed. This vertical direction is called the transmission axis (TA) of the polarizer. A second polarizer known as the analyzer whose transmission axis can be rotated can be used to test the state of polarization. When the TA of the anlayzer is oriented at 90^o relative to the polarizer, the light is effectively extinguished. As the angle is reduced from 90^o to 0^o, the light transmitted through both the polarizer and analyser increases, reaching a maximum at 0^o where the two transmission axes are aligned.

Fig. 2. Malus’ Law. Action of a horizontal metal grid polarizer and a rotatable analyzer on microwaves.

For the arrangement of the optical elements as shown in figure 2, the transmitted electric field amplitude is

and the irradiance S is proportional to the square of the amplitude, hence

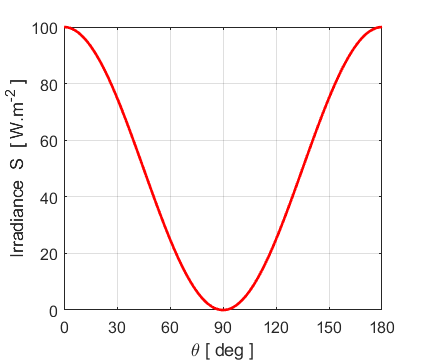
which is a statement of Malus’ law.

Malus’ law applies to all forms of electromagnetic radiation. For visible light, a dichroic polarizer selectively absorbs light with electric field oscillations along a unique direction characteristic of the dichroic material. The dichroic polarizer easily transmits light with electric field oscillations along a direction orthogonal to the direction of absorption. Dichroism means that light propagating in a given direction will be absorbed differently depending on the orientation of the electric field. A naturally occurring material that can act as a dichroic polarizer is the mineral tourmaline. The most common dichroic polarizer is a material called polaroid invented in 1938 by E.H. Land. When a clear sheet of polyvinyl alcohol is heated and stretched, its long hydrocarbon molecules tend to align in the direction of stretching. The stretched sheet is them impregnated with iodine atoms which become associated with linear molecules and provide free (conduction) electrons which act as the free electrons in the metal grid. For dichroic materials, complete cancellation of the forward propagating wave does not occur and most of the energy is dissipated (absorbed) rather than the cancellation due to the interference of the incident wave and the generated wave.

We can use a Matlab Script (op_006.m) to model red light passing through a polarizer and analyser as the analyser is rotated through an angle from 0^o to 90^o where is the angle between the transmission axes of the polarizer and analyser. Figure 3 shows a plot of the irradiance S as a function of angle . The plot is an illustration of Malus’ law. The lower plot shows the light reaching a viewing screen as the angle is varied.

Fig. 3. Crossed polarizers and Malus’ law (figure 2): When the TA axes are parallel, maximum light is transmitted through optical elements. When the two TA axes are perpendicular to each other, minimum light is transmitted.