NUMERICAL ANALYSIS OF OPTICAL AND ELECTROMAGNETIC PHENOMENA

ELLIPTICAL AND CIRCULAR POLARIZED LIGHT

Ian Cooper

matlabvisulaphysics@gmail.com

op_005.m

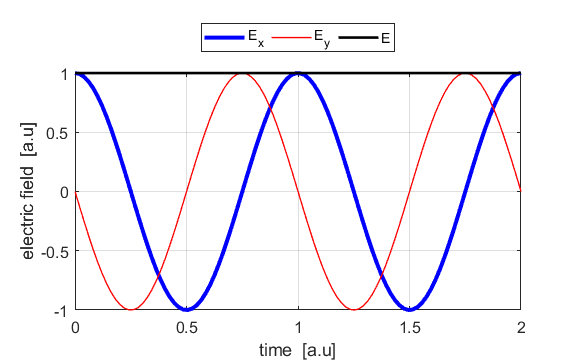
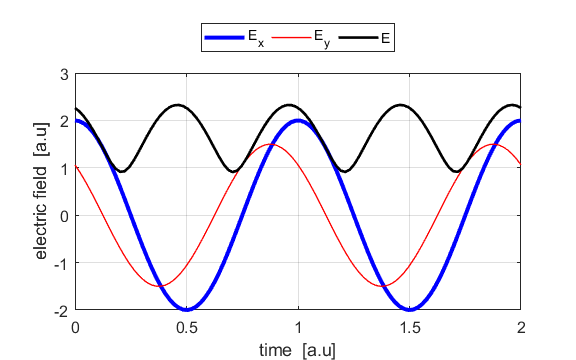
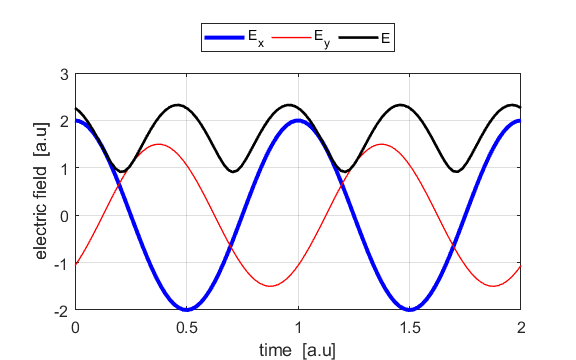
The Script op_005.m can be used to model the any type of polarization. The animations of the electric field vector can be saved as animated gif files (flag1 and flag2). In the INPUT SECTION of the Script, you can enter the amplitudes of the electric field components and their phase angles (flagP = 1) or the Jones parameters (flag2 = 2). 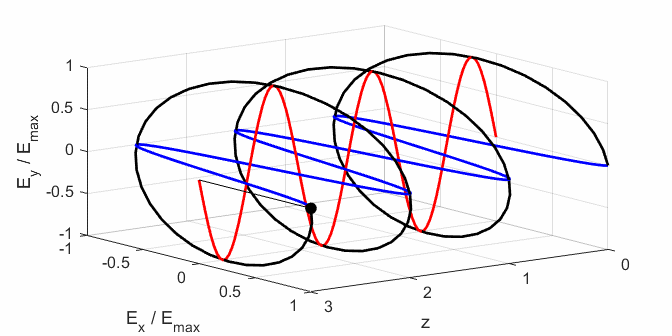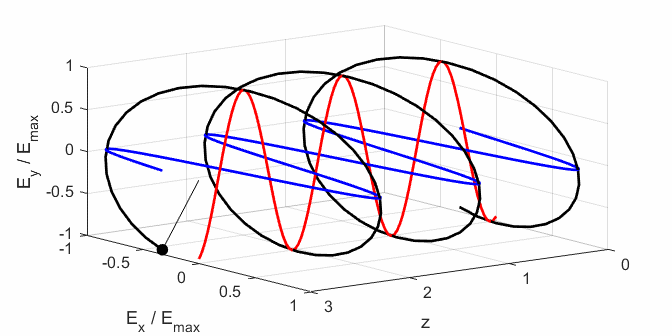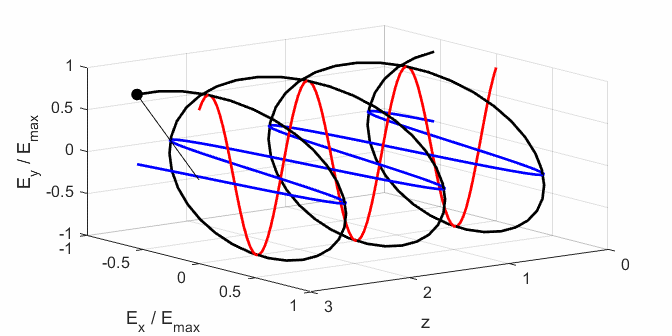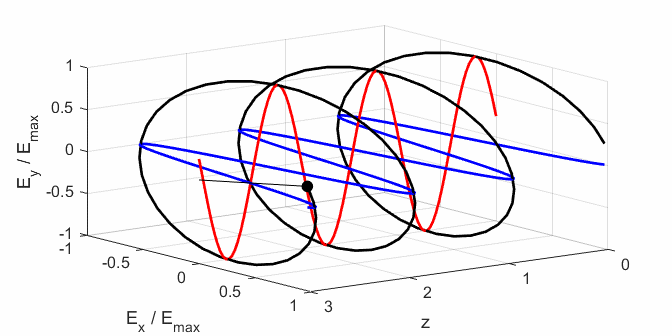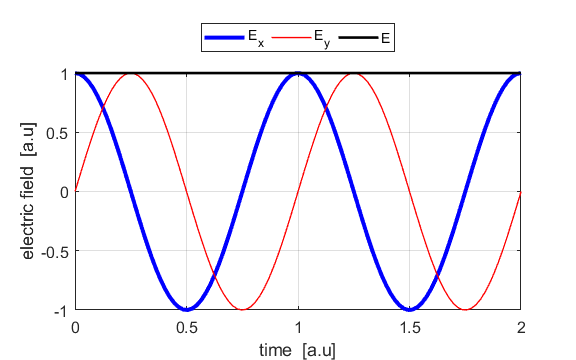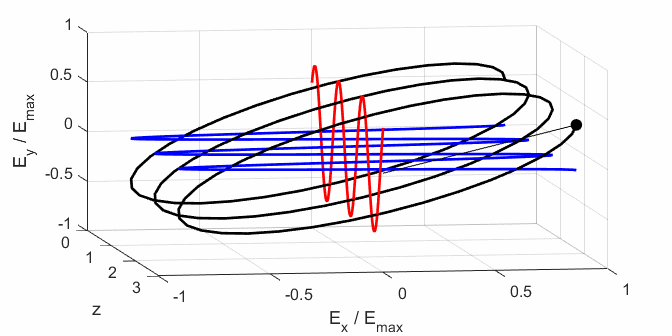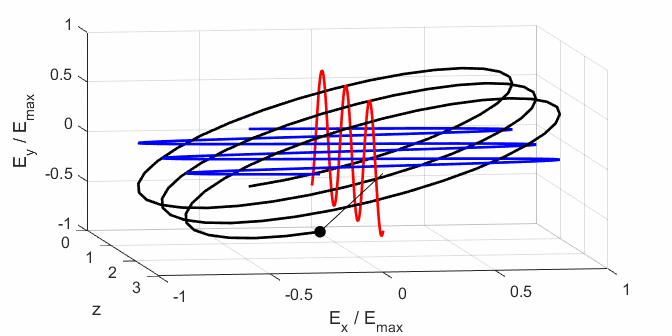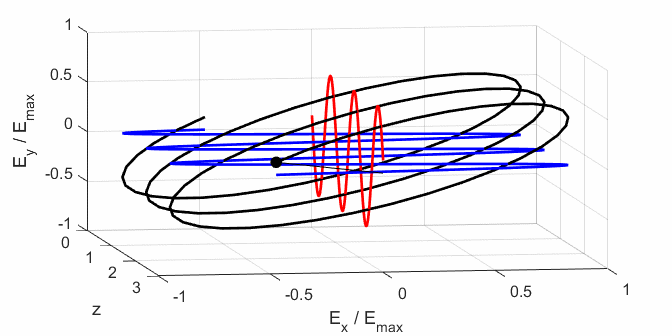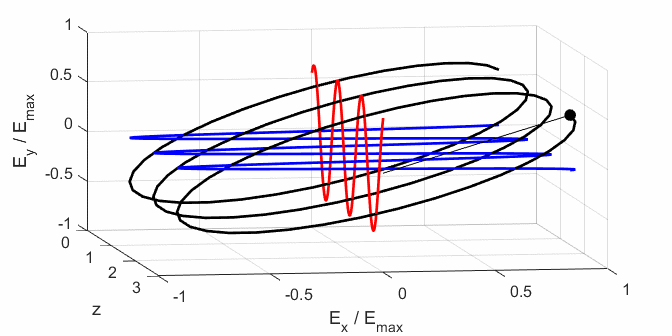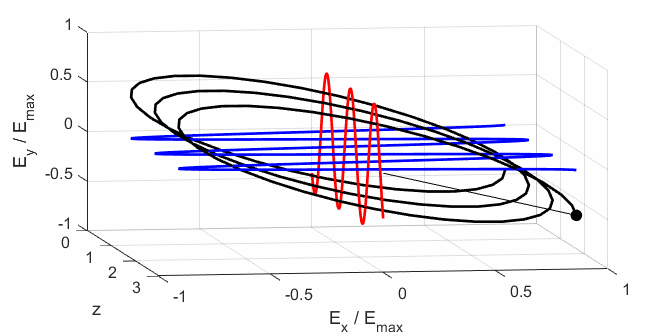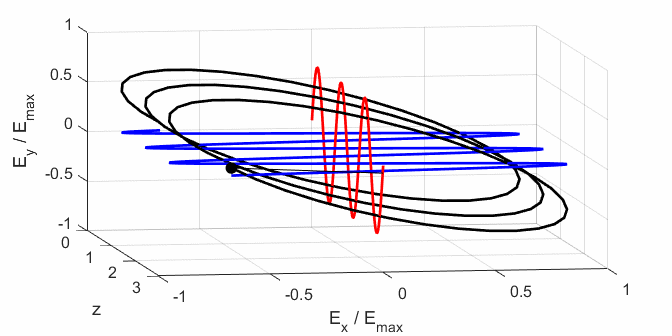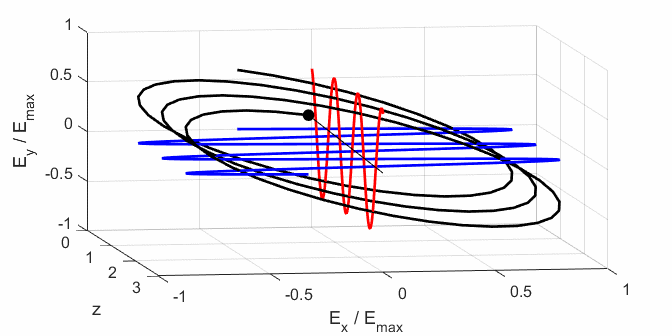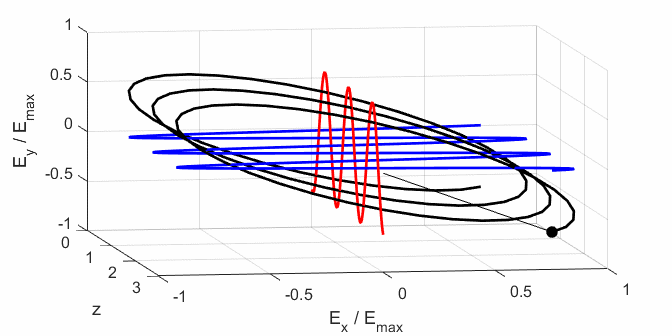From the input values, the electric field (E, Ex, Ey) as functions of time t and position z are calculated. In any plane (z = constant), the electric field vector sweeps out an ellipse with time, a straight line (linear polarization) and a circle (circular polarization) are special cases of an ellipse. 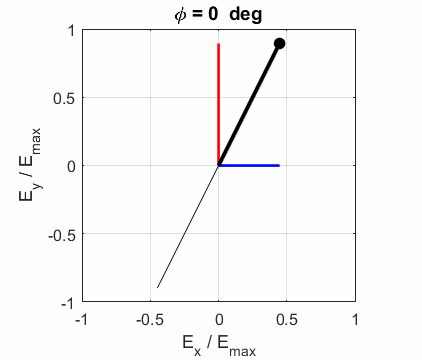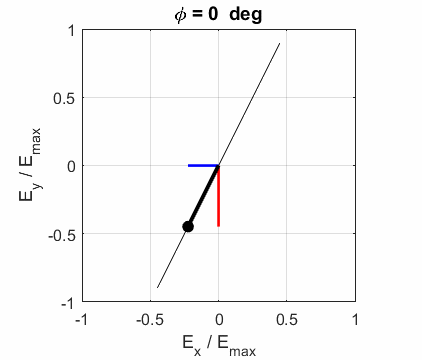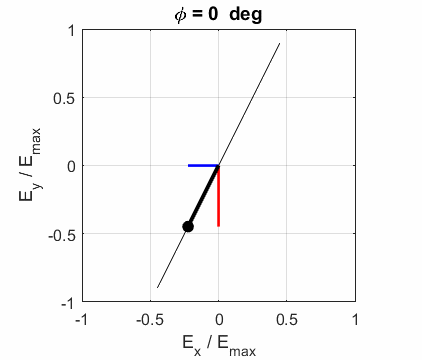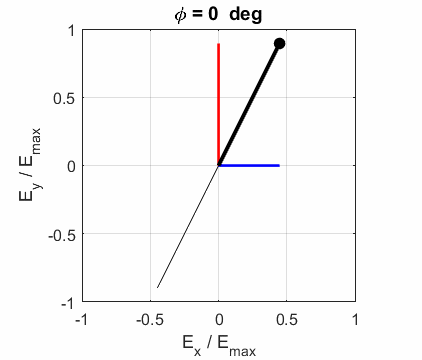The time evolution of the magnitude of the electric field is used to find its maximum Emax and minimum Emin values and the angle for the orientation of the major axis of the ellipse with respect to the X axis.

POLARIZED LIGHT

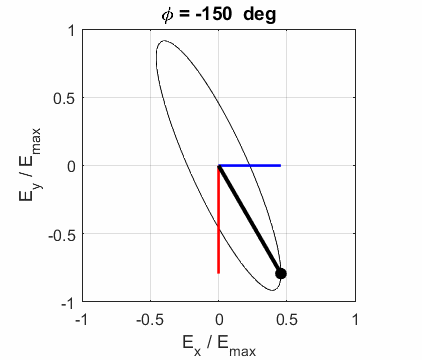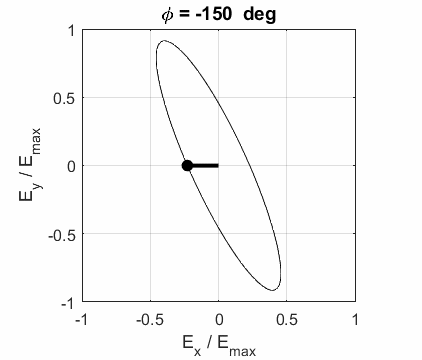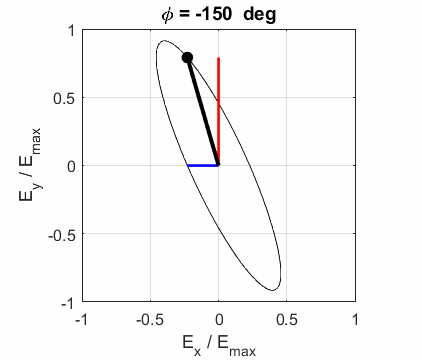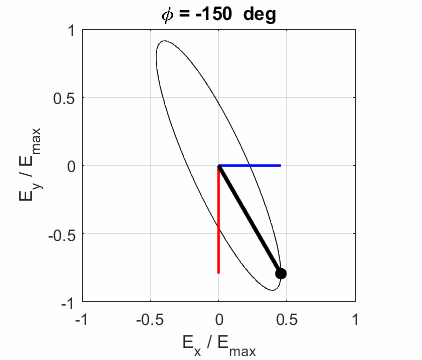
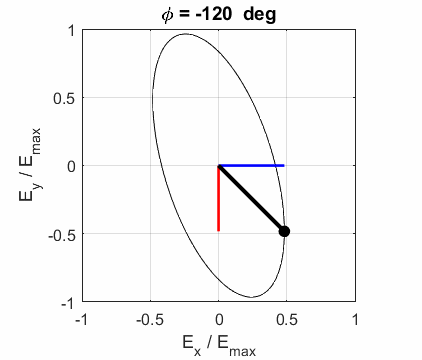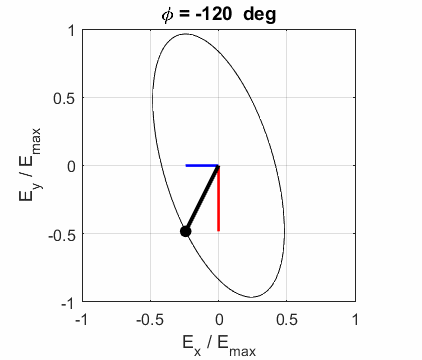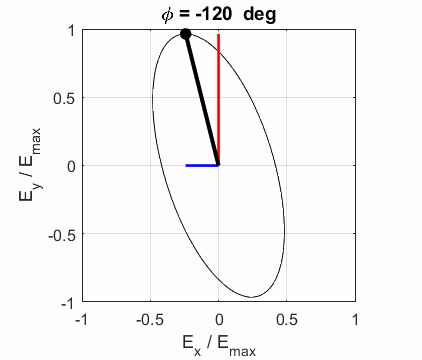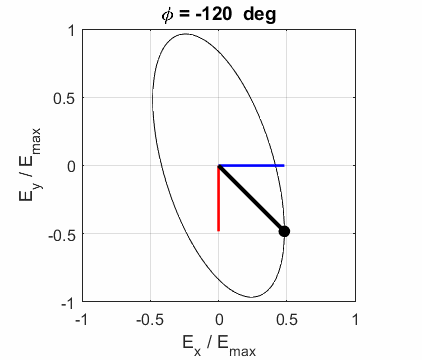
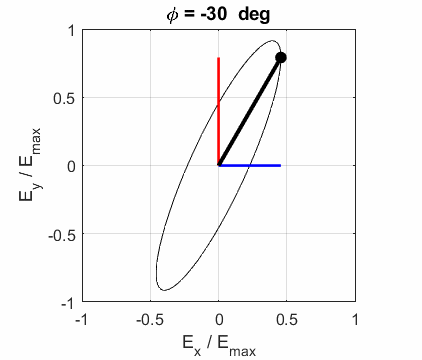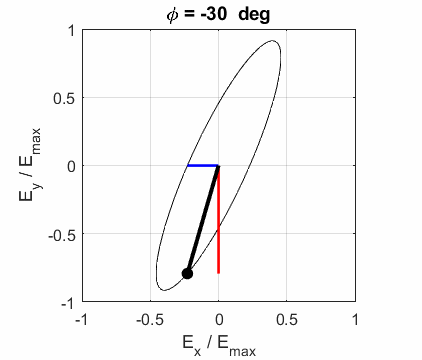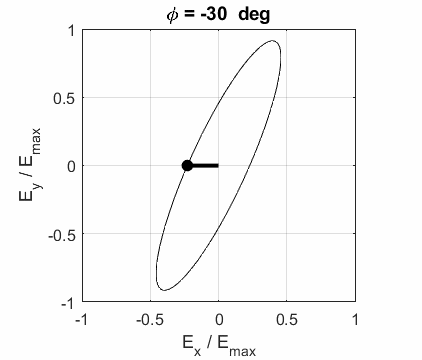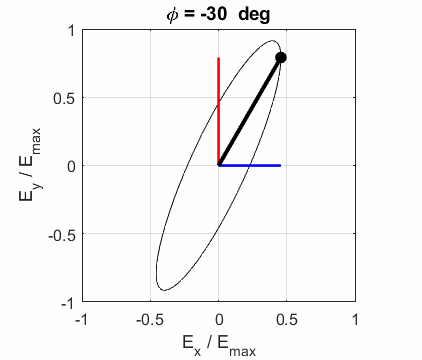
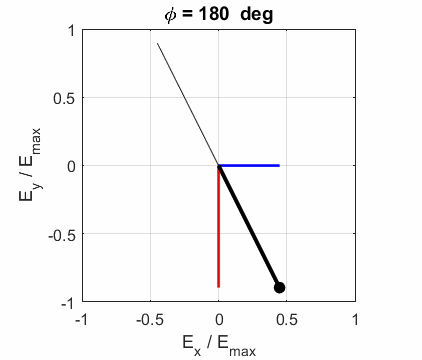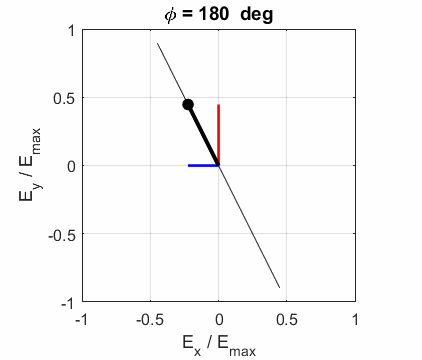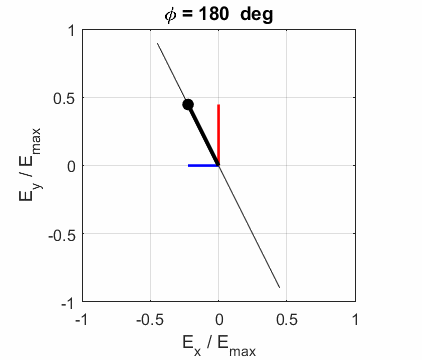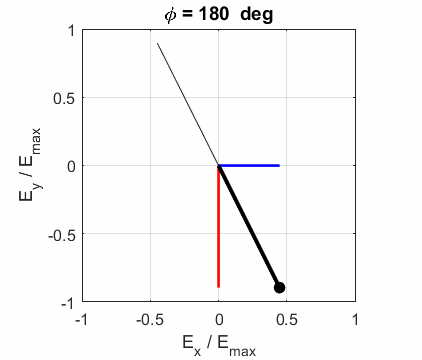
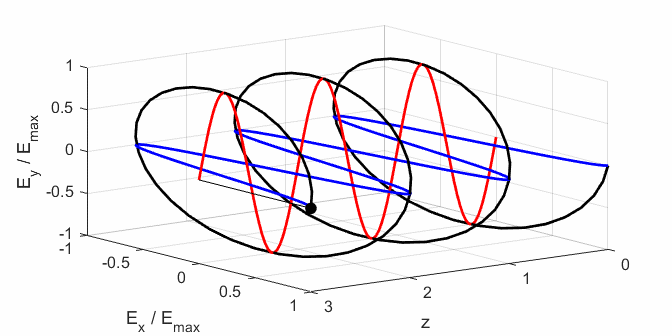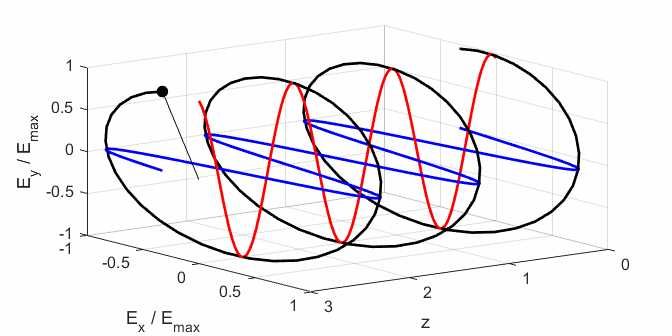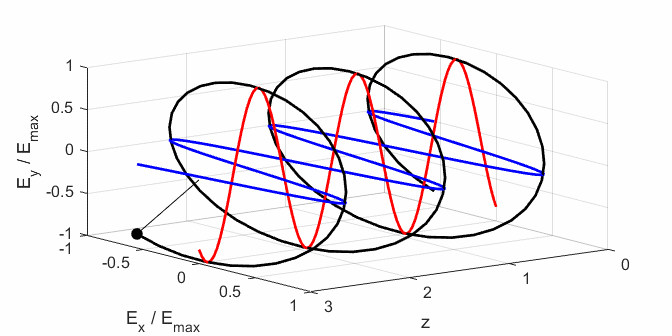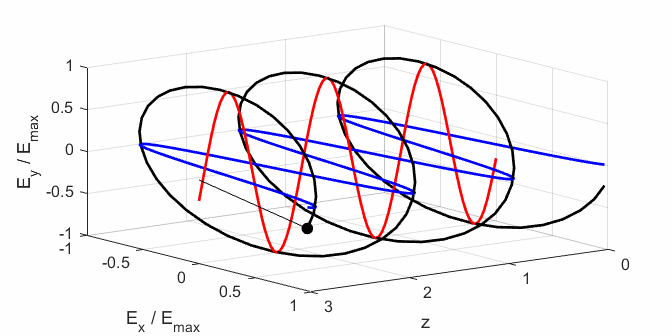
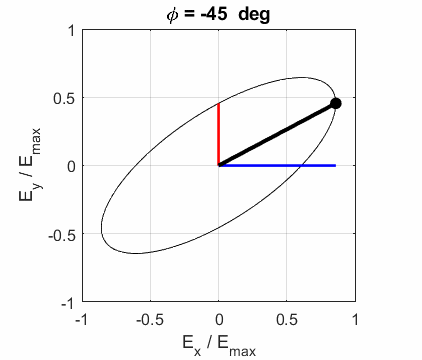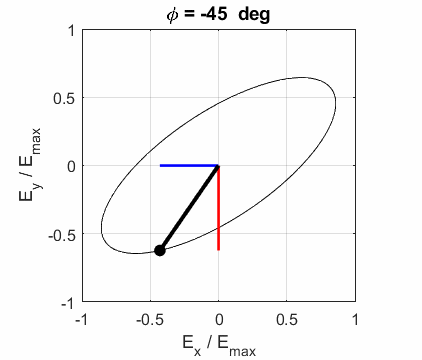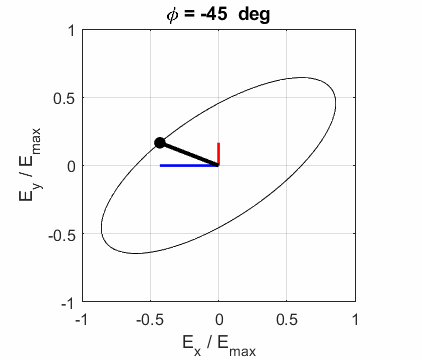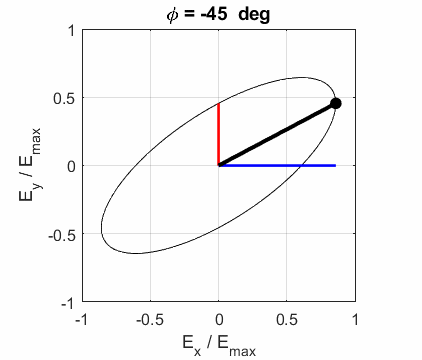
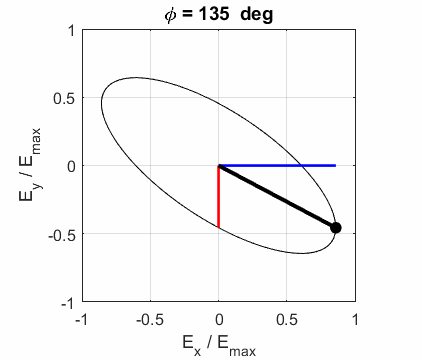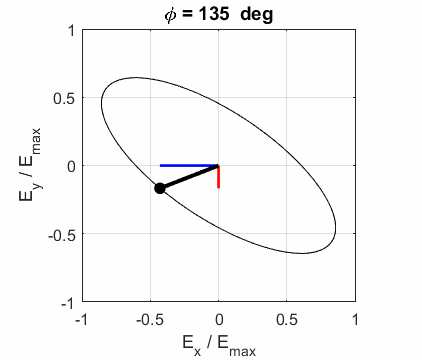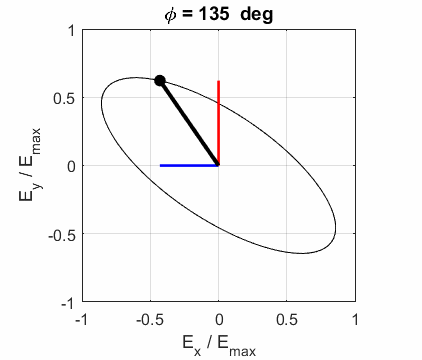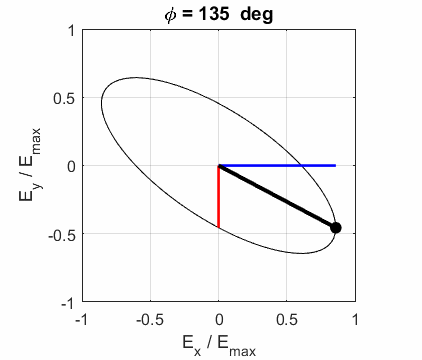
From a mathematical point of view, both linear and circular polarized light may be considered to be special cases of elliptical polarized light. In general, for elliptical polarized light, the electric field vector will change magnitude as it rotates. In such cases, the endpoint of the electric field will trace out an ellipse in any XY plane when the EM wave propagates in the Z direction. The semimajor axis makes an angle relative to the X axis. Using the Script op_005.m, the parameters describing the ellipse are calculated directly from the time evolution the X and Y components of the electric field without the need of the equations describing the ellipse.

Consider the example where

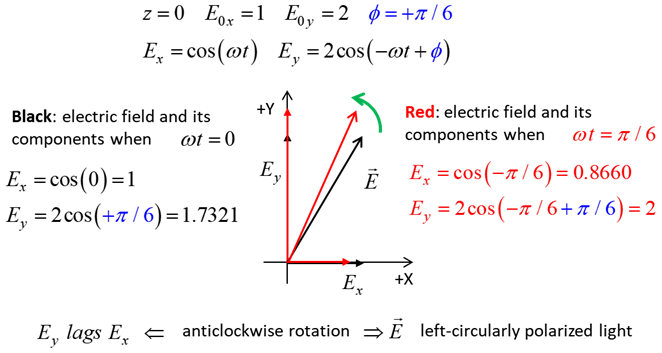
and take the two times such that and . Then, by drawing the electric field vectors at these two times, we can clearly see the sense of rotation of the electric field vector and determine whether the light is left or right polarized as shown in figures 2A and 2B.

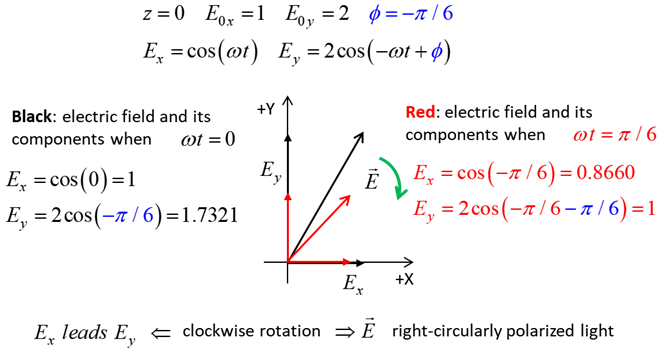
Fig. 2A. Left-polarised light - positive helicity . The electric field vector sweeps out an ellipse in an anticlockwise sense as viewed head-on looking back along the Z axis. The term is used for the phase, so we have to add to the phase of . reaches its maximum value a quarter of a cycle after does.

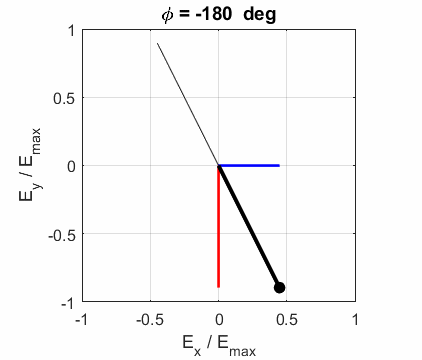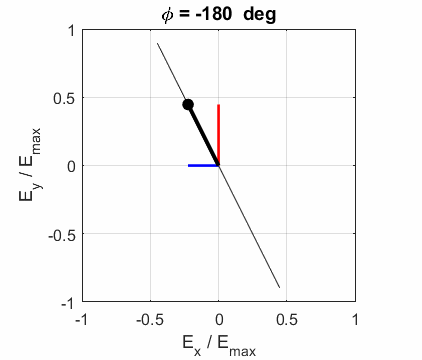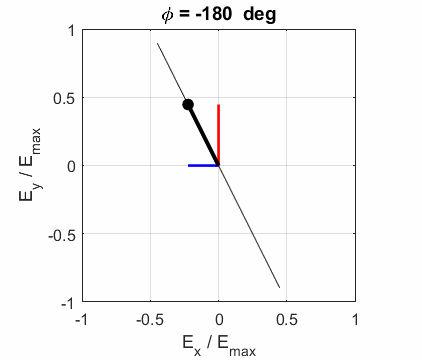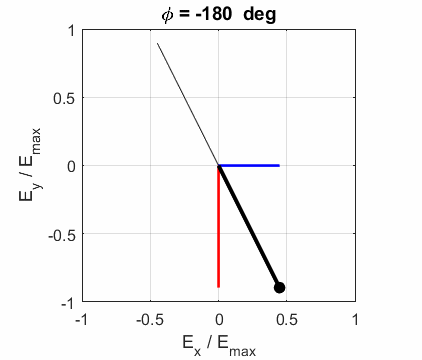
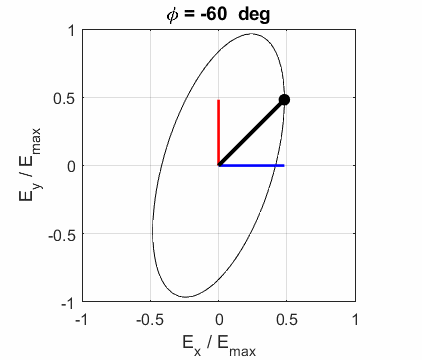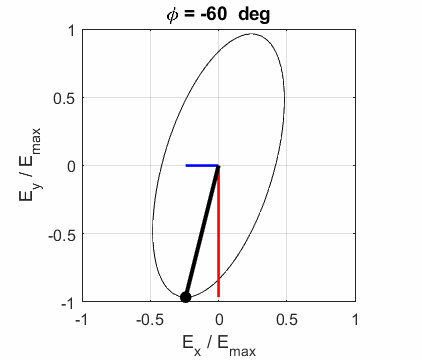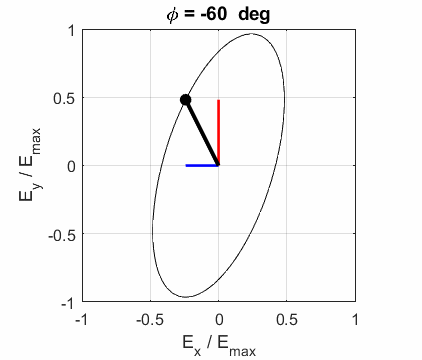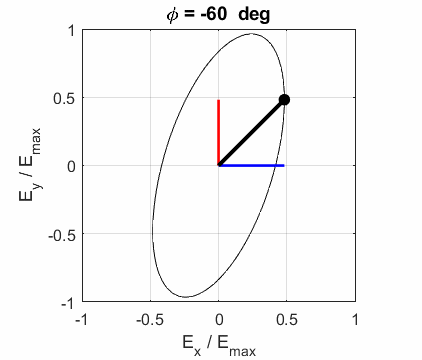
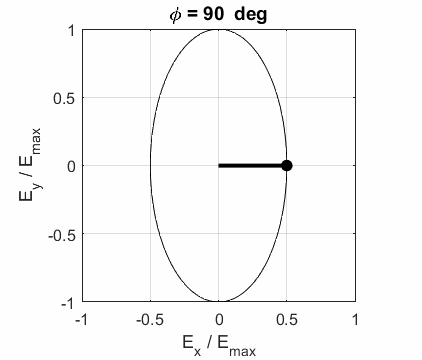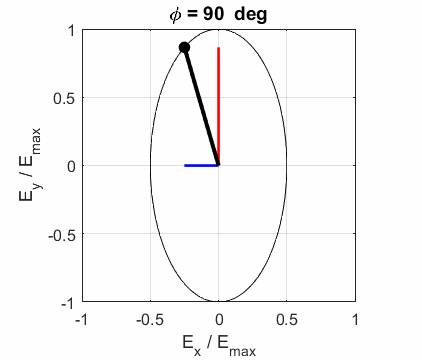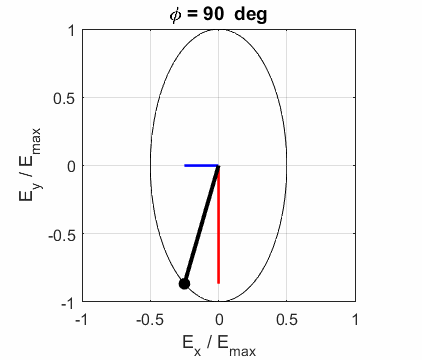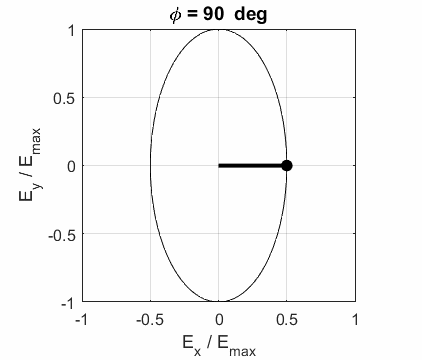
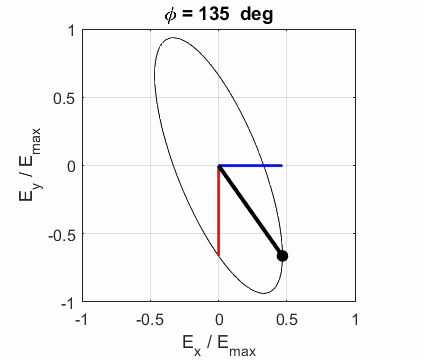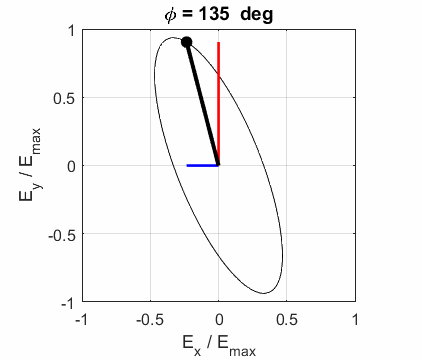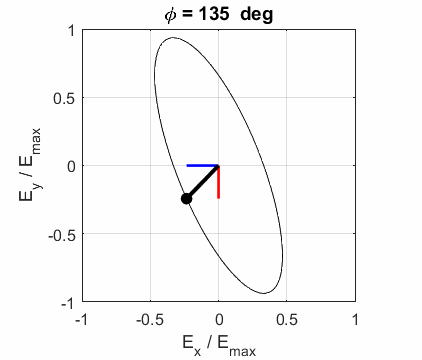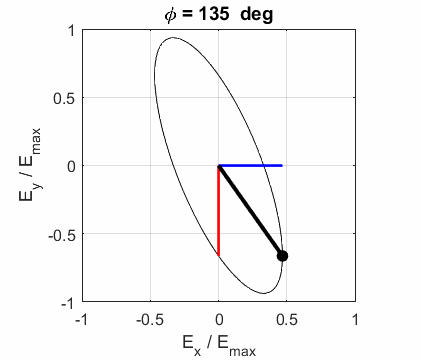
Fig. 2B. Right-polarized light - negative helicity . The electric field vector sweeps out an ellipse in a clockwise sense in any XY plane as viewed head-on looking back along the Z axis. The term is used for the phase, so we have to add to the phase of . reaches its maximum value a quarter of a cycle before does.

The state of polarization depends upon the relative phase The script op_005.m was used to produce the animations.

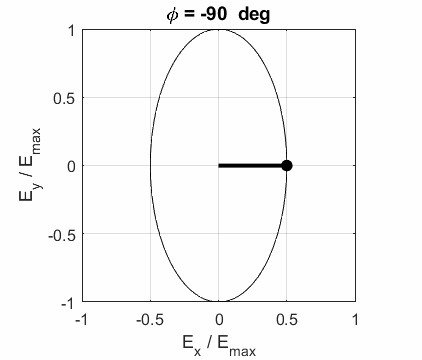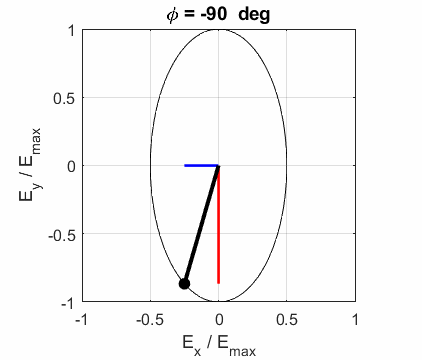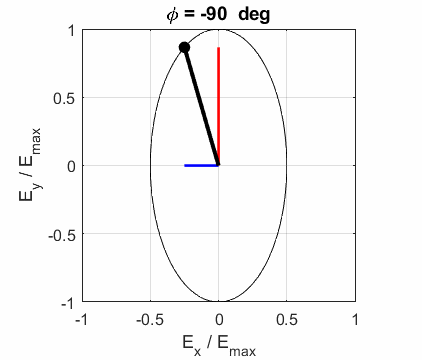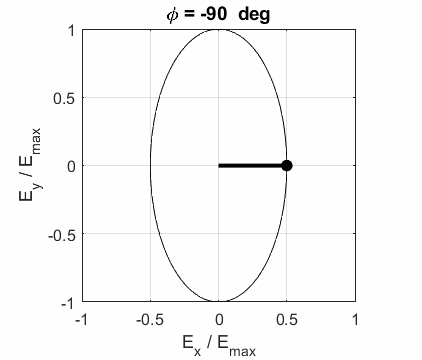
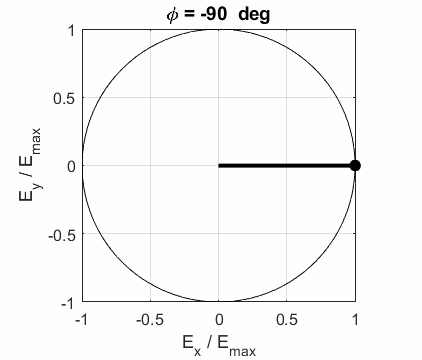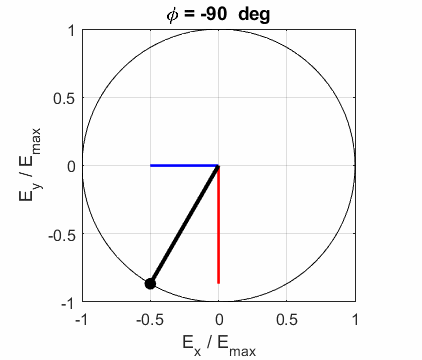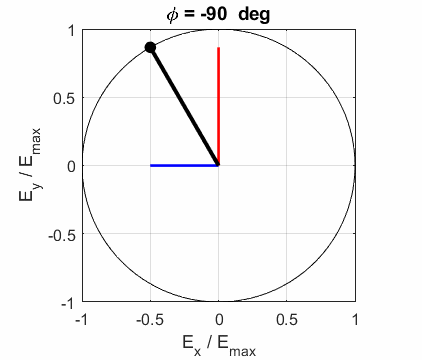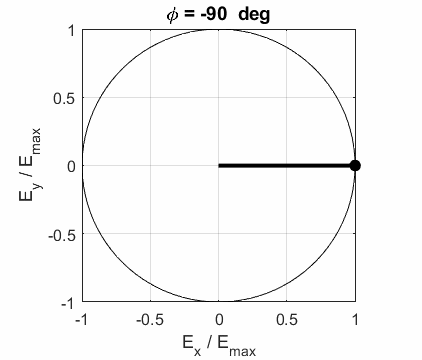
The animations show the time evolution of the electric field and its components for different values of the relative phase angle . From the animations, determine whether the polarization is linear or elliptical with left or right polarization.

CIRCULAR POLARIZED LIGHT

The conditions for circular polarization are:

left circular polarization

right circular polarization

Right circular polarized light

For a fixed value of t, the electric field vector describes a spiral on the surface of a cylinder of radius with its axis along Z. The wave advances one wavelength in a time interval of one period. The resultant electric field vector at each point along the Z axis rotates with an angular frequency . An anticlockwise rotation corresponds to left-circularly polarized and a clockwise rotation is referred to as right-circularly polarized light.

Left circular polarized light

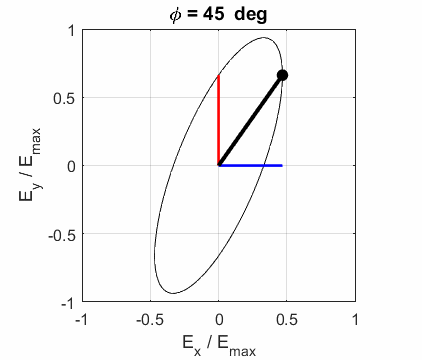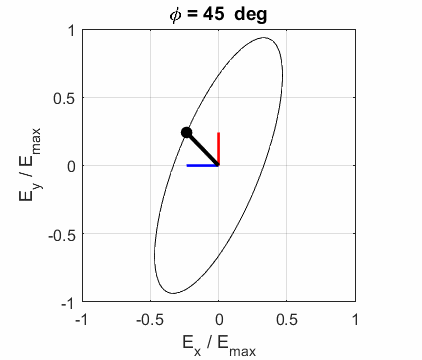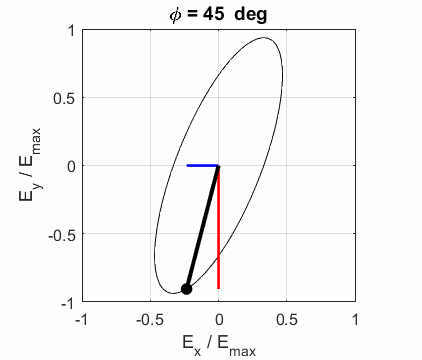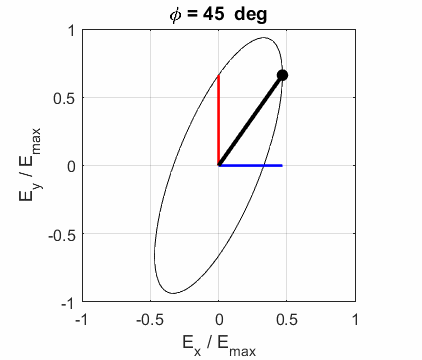
ELLPTICAL POLARIZED LIGHT

Right Elliptical polarized light

Left Elliptical polarized light