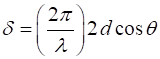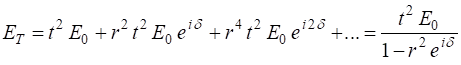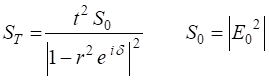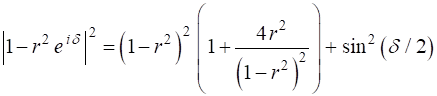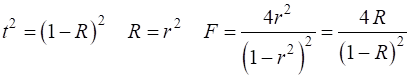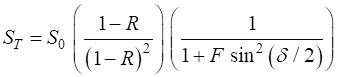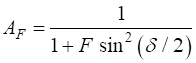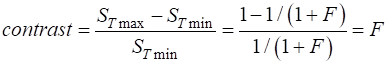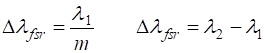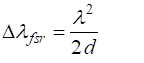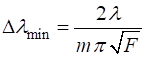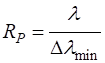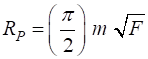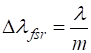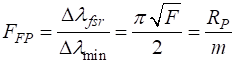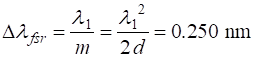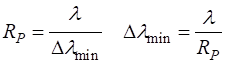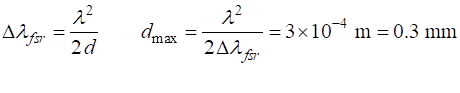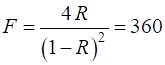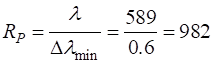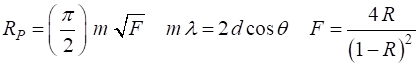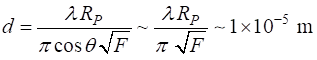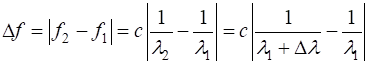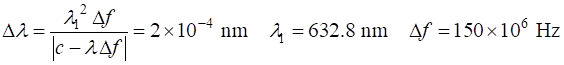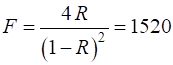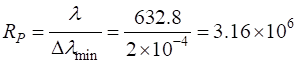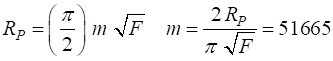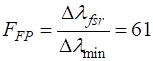DOING PHYSICS WITH MATLAB

NUMERICAL ANALYSIS OF OPTICAL AND ELECTROMAGNETIC PHENOMENA

FABRY – PEROT INTERFEROMETER

Ian Cooper

matlabvisualphysics@gmail.com

Matlab Script Download Directory

op_LE_010.mlx

Live Editor Script for the modelling the operation of a Fabry-Perot interferometer. The Fabry-Perot interferometer is instrument used in precision wavelength measurements and has extremely high resolution. The modelling allows one to investigate the general features of the interferometer. The instrument is very sensitive, so you need to be careful in changing the input parameters. You may need to adjust the limits for the slider controls. It is best to Disable Synchronous Scrolling of the Output Window. The interferometer is an extremely sensitive instrument. Slight variations in the input parameters can dramatically change the irradiance distribution. Rather than use a trial and error approach to altering the variables, we can estimate a possible range for the separation distance between the interferometer plates from the inputs of reflectance, wavelength and wavelength increment. The minimum distance between the plates is estimated from the resolving power and the maximum separation distance of the plates is estimated from the free spectral range. A summary in the Output Window for possible values of the plate separation distance and maximum viewing angle for the irradiance distribution are displayed. These values then can be entered into the controls (inputs) for the plate separation distance and max angle for viewing the irradiance distribution. The Script calls the function colorCode.m to assign a color that matches the wavelength of visible light to its “true” color.

op_010A.m

Script used for plotting the coefficient of finesse F and the Airy function A_F.

Fabry-Perot Interferometer

The Fabry-Perot interferometer uses multiple-bean interference to measure wavelengths with high precision and accuracy and to study the fine structure of spectrum lines. This instrument is probably the most adaptable of all interferometers. It is used for the determination of the refractive indices of gases and the calibration of the metre in terms of wavelength. The instrument was devised in 1899 by C. Fabry and A. Perot. The Fabry-Perot instrument is essentially two parallel optically flat and partially reflecting plates of quartz or glass. The surfaces must be extremely flat and parallel to obtain the maximum fringe sharpness (a flatness of the order of 1/20 to 1/100 wavelength is necessary). If the space between the reflecting plates is fixed, the instrument is called an etalon. If the plates are movable, then the device is called an interferometer. 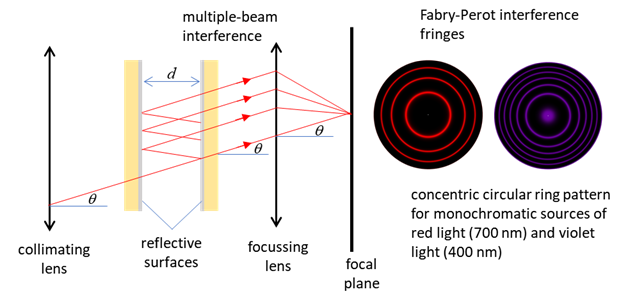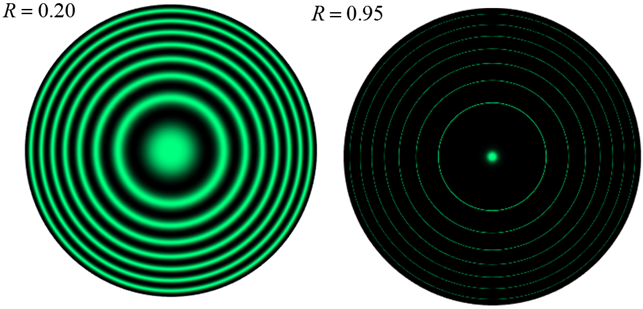In use, the interferometer is usually mounted between a collimating lens and a focussing lens. 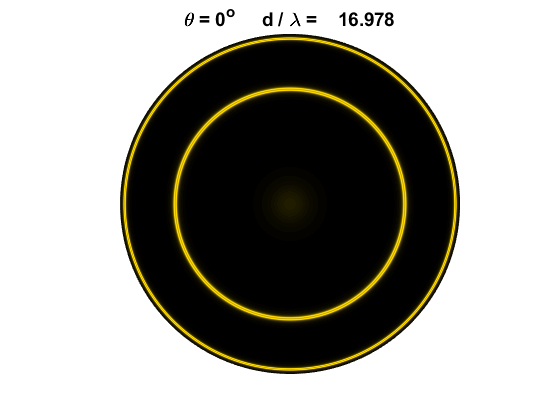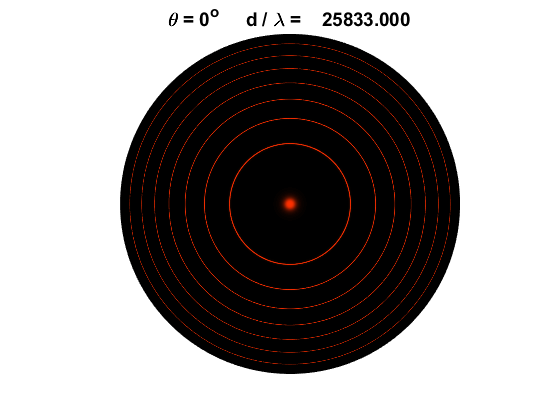The interference fringes form a set of circular concentric rings in the focal plane of the focussing lens as shown in figure 1.

Fig. 1. Fabry-Perot interferometer. The fringe patterns were created using the Script op_LE_010.mlx. Each ring is specified by its order m. Generally, the plate separation distance d is much larger than the wavelength , so the circular fringes seen on the screen are for large m values. Note, that the larger the diameter of the circular fringe, the smaller the value of m.

Consider a narrow, monochromatic beam (wavelength ) from an extended source making an angle w.r.t. the optical axis of the optical system as shown in figure 1. The single beam from the source produces multiple coherent beams in the interferometer and emerges as a parallel beam and then brought to a focal point by the focussing lens. The nature of the superposition at the focal point depends upon the path difference between successive parallel beams. The optical path difference can be expressed as

(1)

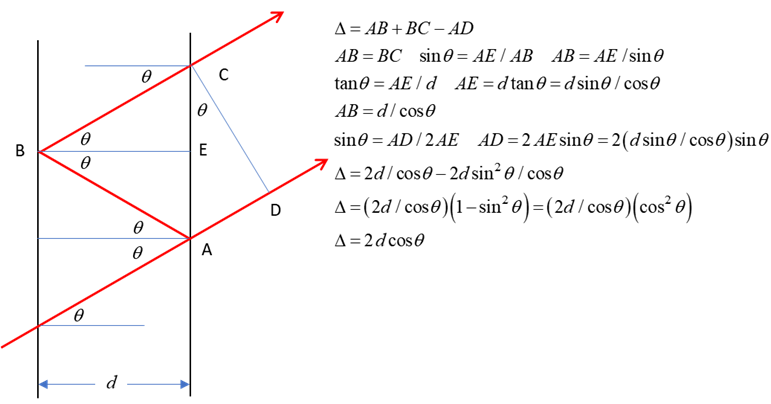
Fig. 2. Interference of light travelling through the space between the reflective plates depends on the path difference between successive reflected beams.

Thus, the phase difference between successive reflected beams is

(2)

When a single ray of light strikes one of the reflective surfaces (mirrors) with amplitude , the amplitude of the reflected ray is and the amplitude of the transmitted light is where is the coefficient of reflection and is the coefficient of transmission. By conservation of energy (assume no absorption of energy) then

or

where is the reflectance and is the transmittance.

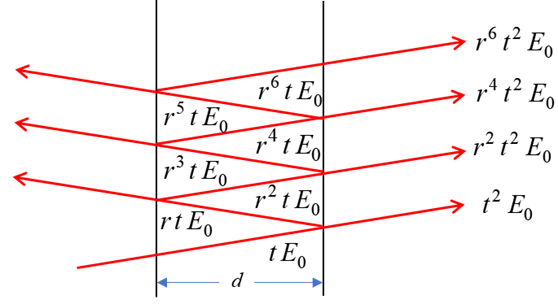
Fig. 3. Paths of light rays in multiple reflection between the two reflective surfaces.

From figure 3, and taking into account the factor (equation 2) and adding the amplitudes of all the transmitted rays, we get the expression for the superposition of the electric field from all the rays

(3)

A phase change may occur on reflection. However, in this case the total phase change due to the two successive reflections can be taken as zero.

The irradiance (intensity) of the transmitted light is and is thus given by

(4) transmitted irradiance

(5) Airy function

(6) coefficient of finesse

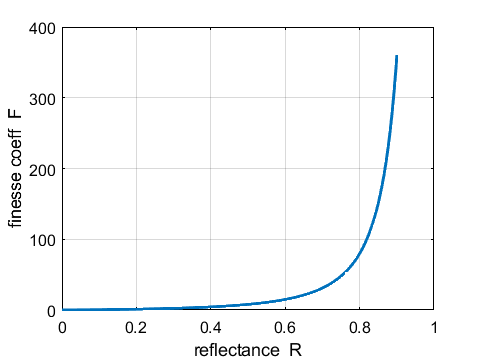
The coefficient of finesse is a measure of the sharpness of the interference fringes (measure of the fringe contrast). The coefficient of finesse is a sensitive function of the reflectance (or reflection coefficient ). As varies from 0 to 1, varies from 0 to infinity. If is small, the interference fringes are broad and distinct, whereas if is close to 1, the fringes are very sharp.

Fig. 4. Coefficient of finesse F as a function of reflectance R. op_010A.m

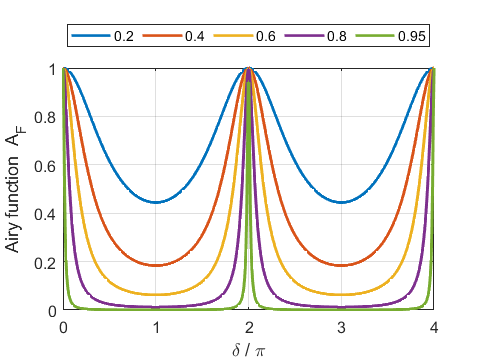
Fig. 5. Airy function for different values of reflectance R as a function of phase angle . The Airy function gives the irradiance S distribution of the fringes in multiple-beam interference. For each curve, the maximum values occur at and the minimum values at where . Notice that regardless of the value of the reflectance R. However, is never zero, but approaches zero as R approaches 1. The transmitted irradiance peaks sharply at higher values of R as the phase difference approached integer multiples of and remaining nearly zero otherwise. op_010A.m

The transmitted irradiance is a maximum when and a minimum when (figure 5).

The path difference between successive transmitted rays is given by equation 1

(1)

A peak in the irradiance distribution (ring) due to constructive interference of the multiple beams occurs when this path difference is an integer multiple of the wavelength, hence

(7) constructive interference (peak - ring)

where m is called the order for the interference. Equation 7 describes the set of circular rings in the irradiance distribution as shown in figure 1.

The fringe contrast is measured by F (coefficient of finesse)

The fringe contrast values for the plots shown in figure 5 are displayed in the Command Window using the Script op_010A.m

R contrast

0.20 1

0.40 4

0.60 15

0.80 80

0.95 1520

Free Spectral range

It is useful to define the free spectral range of the instrument , the wavelength separation between adjacent orders of interference. Individual rings for each wavelength occur in the interference pattern of the Fabry-Perot interferometer. This means that this complex interference is difficult to interpret unless some means are found to limit the range of wavelengths analyzed by the interferometer. For example, consider two wavelengths such that .

When is small, the two sets of ring fringes with the same order m will be close together. However, as increases, the fringes separate. When the separation of the fringes becomes equal to the separation between consecutive orders, confusion of the orders occurs. We can calculate the wavelength difference such that the m^th order of overlaps the order (m+1) of . This wavelength difference is called the free spectral range of the interferometer. The free spectral range is the change in necessary to shift its circular fringe pattern by the distance of consecutive orders.

The optical path difference is expressed as

(1)

For constructive interference, the optical path length must equal an integer multiple of the wavelength . So,

(8) wavelength difference when two orders overlap

Near the centre of the circular fringe pattern is small, hence, and , so the free spectral range can be expressed as

(9)

To avoid associating fringes of one order with those of the next, then we should have

Resolving Power

The accuracy with which the Fabry-Perot interferometer can measure wavelengths depends upon the smallest wavelength difference that can be reliably detected. Suppose a spectrum consisting of two closely-spaced wavelengths and is to be analyzed with a Fabry-Perot interferometer. The irradiance distribution S_T in the fringe pattern is a combination of the two individual fringe patterns resulting in a double set of circular fringes. For equal irradiance maxima, in order that the two lines be resolved, there must be a dip in the irradiance distribution. The minimum wavelength separation that can be resolved by the instrument depends on one’s ability to detect the dip between the two peaks. A generally accepted convention for the resolution of the two lines is the Rayleigh criterion where the two equal lines are resolved if the irradiance at the saddle point is not greater than times the irradiance maxima . It can be shown that, this minimum difference in the two wavelengths is given by

(10)

where may be either wavelength or their average, since they are very close in value.

The resolving power of any spectroscopic instrument is defined as

(11)

For a Fabry-Perot interferometer, the resolving power R_P as a function of the reflectance R of the mirrors is

(12)

This resolving power of the Fabry-Perot interferometer has a critical dependence on the reflectance R, since the fringes become very sharp as R approaches 1 (figure 4). The resolving power of a good Fabry-Perot interferometer can exceed one million which is 10 to 100 times greater than the resolving power of a prism or grating spectroscope. Large resolving powers are a desirable feature of an interferometer. Large values of the resolving power occur when the order m is large near the centre of the fringe pattern and for large coefficient of finesse F. To maximize the order m at the centre of the rings, requires the plate separation d to be as large as possible. Large values for the coefficient of finesse F corresponds to high reflectance R values.

The free spectral range is , hence a larger value of the order m means an undesirable value for the free spectral range. However, the resolving power is better for larger the order. Alternatively, we want

to be as large as possible and

to be as small as possible.

Hence, a large order m is detrimental to a large free spectral range whereas it is favourable to good resolution.

We can give a number to represent a figure of merit for the Fabry-Perot interferometer which is called its finesse . The finesse is defined by the ratio

(13)

A large finesse of the interferometer represents the best compromise between the demands of free spectral range and resolution.

Matlab Explorations op_LE_010.mlx

Run the Script with the inputs

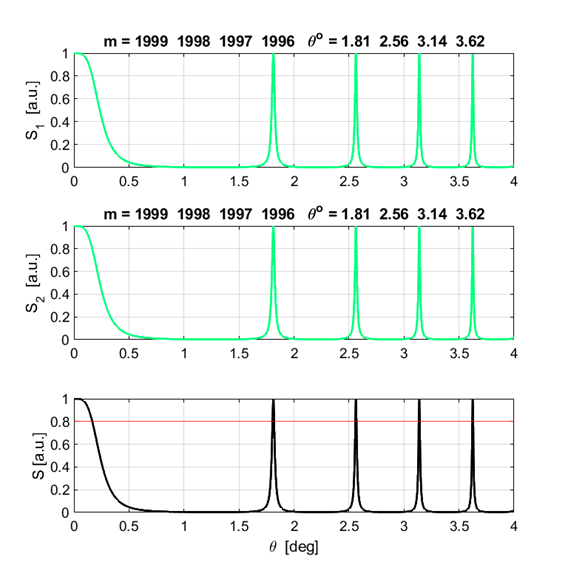
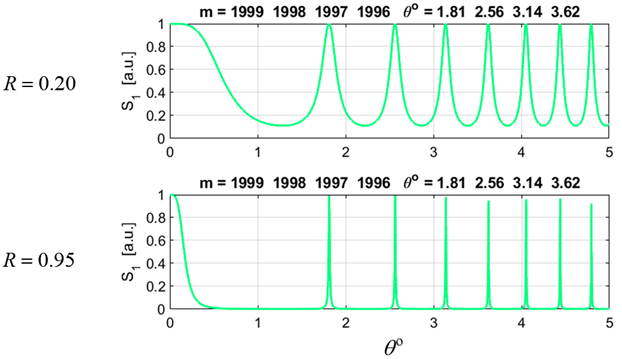
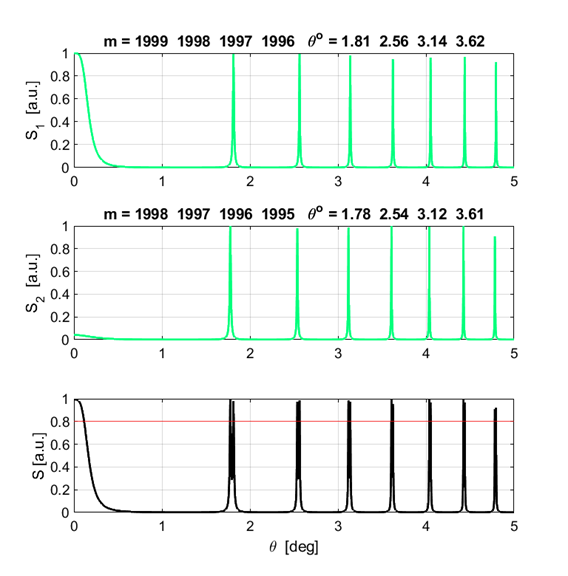
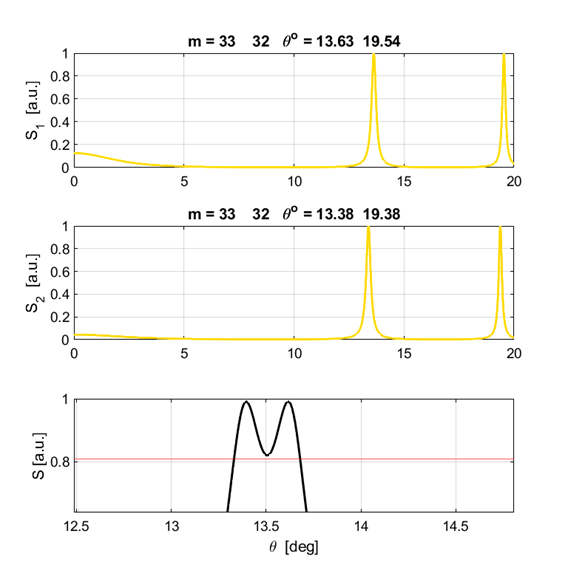
Note, the distance d was set to .

The Script has four output sections as shown in figures 6, 7, 8 and 9.

Fig. 6. Normalized irradiance distribution for each individual wavelength and the resultant distribution. The titles give the order and their corresponding angles for the interference peaks.

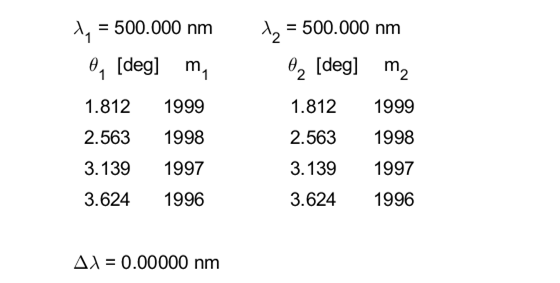
Fig. 7. Table showing the angles for each peak specified by its order m.

Fig. 8. Table of numerical values for the main parameters describing the Fabry-Perot interferometer.

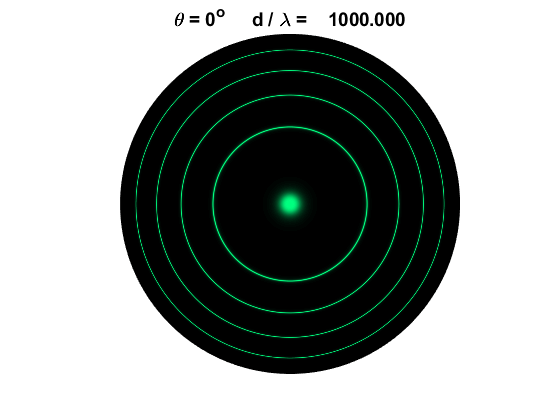
Fig. 9. Concentric circular (ring) fringes for the Fabry-Perot interferometer.

Equation 7 describes the angle at which the peaks occur in the irradiance distribution.

(7) constructive interference (peak - ring)

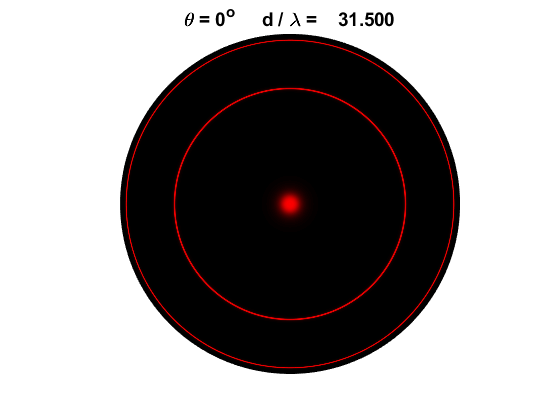
The order m of the peaks decreases with increasing values of as indicated in figures 6 and 7.

If there is a peak at the center of the fringe pattern then an integral number of wavelengths must be equal to the to the distance . For figures 6 and 7, the order of the peak at the center of the rings is . Each successive beam adds constructively, giving a bright spot at the centre of the fringe pattern.

Changing the plate separation distance

When the distance d is set to each successive beam is half wavelength out of phase and all the multiple beams adds destructively to give a dark spot at the centre of the fringe pattern (figure 10).

Input parameters

Fig. 10. Normalized irradiance fringe pattern with a dark center.

Change the plate separation distance in small increments and observe how the positions of the rings change

Input parameters

d (x10^-4 m)

5.000 1.813

5.005 3.137

5.010 4.048

As d increases the angle for the order m increases – the rings move outward

Change the wavelength in very small increments and observe how the positions of the rings change

Input parameters

Fig. 11. As the wavelength is increased, the rings move inward .

Change the reflectance and observe the changes in the fringe pattern.

Input parameters

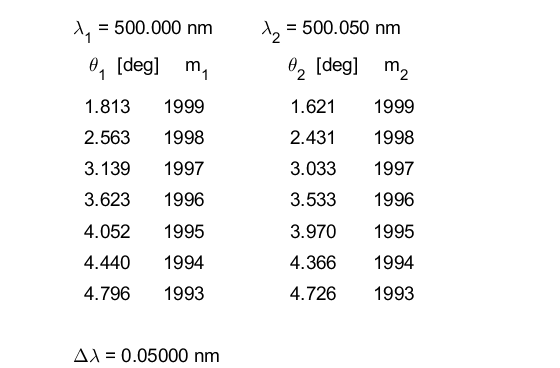
Fig. 12. The rings become sharper (peaks narrower) as the reflectance R increases.

Free spectral range: Slowly increase the wavelength difference to find the free spectral range.

Input parameters

Equations 8 and 9 give the theoretical estimate for the free spectral range

which agrees with the simulation value for given when the order 1998 overlaps the order 1999

0.100 2.293

0.200 1.985

0.220 1.919

0.230 1.885

0.240 1.849

0.250 1.813

0.260 1.777

Fig. 13A.

Fig. 13B.

Resolution / Resolving Power: Adjust the wavelength difference to resolve the peak of order for the two wavelengths.

Input parameters

We can calculate the minimum wavelength difference to resolve two peaks from the resolving power of the interferometer

(12)

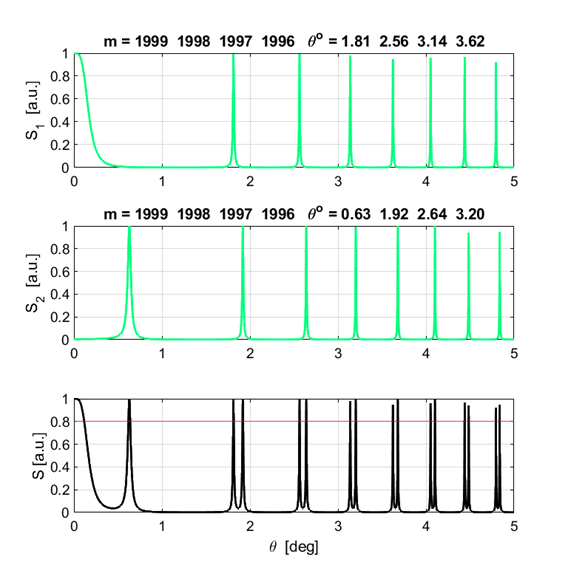
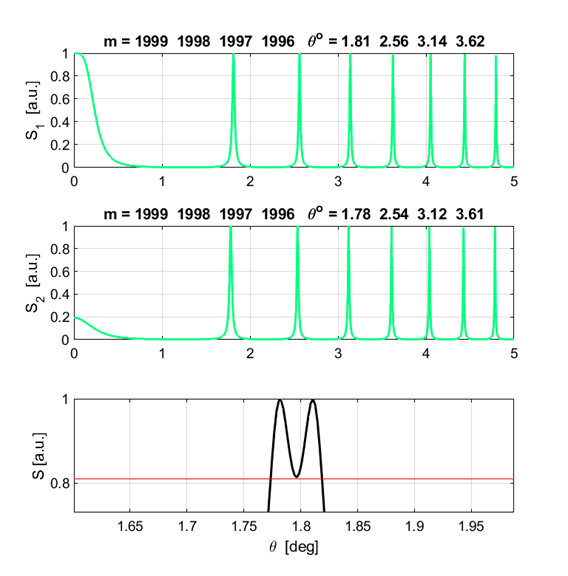
(12)

(11)

A summary of the calculations is given in one of the Output Windows

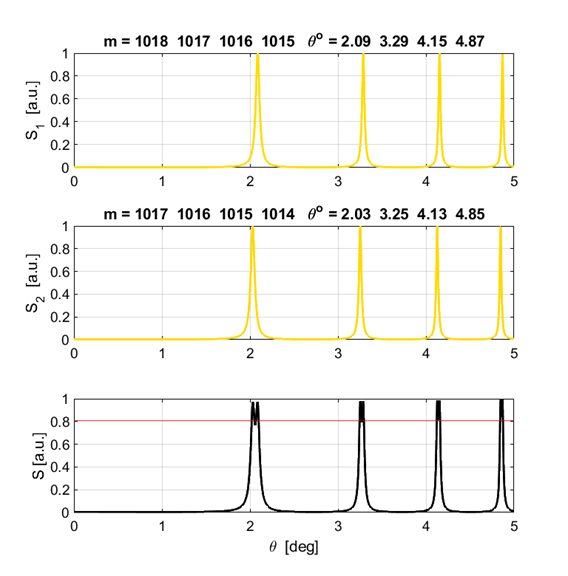
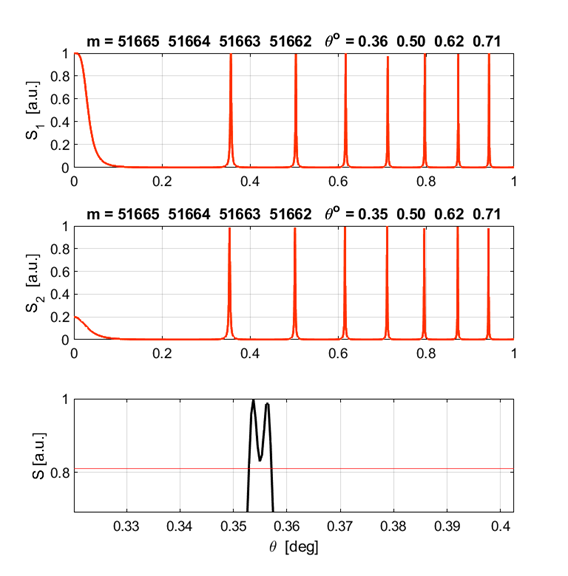
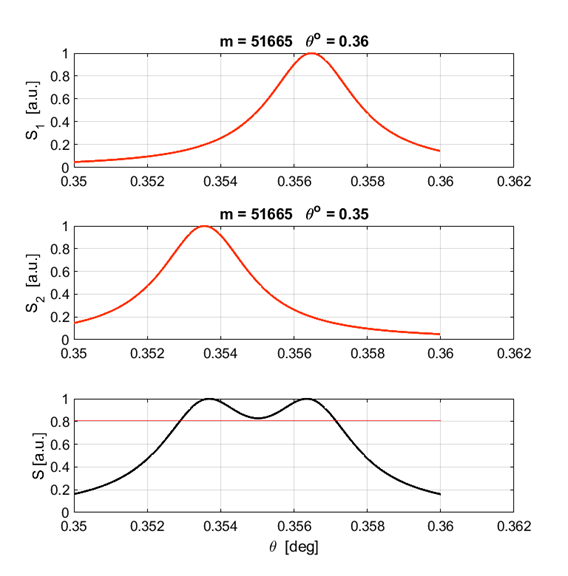
Running the Script, the minimum wavelength difference using the Rayleigh criteria is . To observe the dip in the peak of order 1999, you need to use the zoom function or change the range for the angle (figure 14).

Fig. 14. The irradiance pattern for the peaks the same strength and of order m = 1999. The dip between the two peaks of different wavelengths satisfies the resolution criteria (0.81). We say that the two peaks are resolved for the minimum wavelength separation

.

The sodium doublet lines

The well-known D line in the spectrum of sodium is a doublet with the two distinct spectral lines of wavelengths 580.0 and 589.6 nm. For a Fabry-Perot interferometer with reflectance , what is the range for the plate separation distance d for the two sodium lines to be resolved?

The maximum separation of the plates is limited by the free spectral range. The value for the free spectral range is

Using equation 9, we can thus calculate the maximum plate separation

(9)

So that there is no confusion between the orders, the plate separation must be less than the maximum plate separation, .

Fig. 15. If the plate separation is too large, the orders of the peaks overlap leading to confusion in interpreting the irradiance distribution. Notice, peak 1017 () occurs at a smaller angle than peak 1018 ().

For , the coefficient of finesses of the instrument is

(6)

and the resolving power is

(11)

For a Fabry-Perot interferometer, the resolving power R_P as a function of the reflectance R of the mirrors is

(12)

Hence, we can estimate the smallest plate separation to resolve the two sodium D lines

Input parameters

H line doublet (textbook style problem)

The reflectance of the plates of a Fabry-Perot interferometer is 0.96. Use the Script op_LE_010.mlx to resolve the doublet for the lines where

.

m_min = 63.00 m

d_min = 2.06728515e-05 m

d_max = 1.58347335e-03 m

theta_max_min = 10.22 m

theta_max_max = 0.90 m

He-Ne laser (textbook style problem)

A Fabry-Perot interferometer with a plate reflectance of 0.950 is to be used to resolve the mode structure of a He-Ne laser operating at 632.8 nm. The frequency separation between modes is 150 MHz. Determine: (a) the minimum resolvable wavelength interval; (b) coefficient of finesse; (c) the resolving power (resolution); (d) the plate separation distance to resolve the two laser lines; (e) free spectral range; (f) the finesse.

From the frequency separation, we can calculate the difference in the two wavelengths of the laser light.

Coefficient of finesse (equation 6)

The required resolving power (equation 11)

The resolving power is also given by equation (12). Therefore, the order m of a fringe to be resolved must be

The minimum plate separation d to resolve the two spectral lines is approximately given by (equation 7)

The free spectral range is given by equation 8

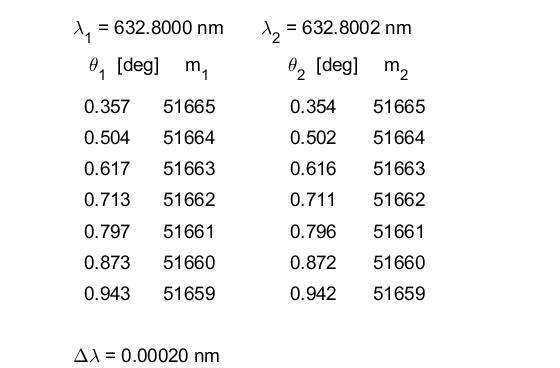
Note: there will be no confusion of the orders, since . The finesse of the instrument is (equation 13)

We can run the Live Editor Script op_LE_010.mlx to confirm the above calculations.

Input parameters

The value for the value of d was found by typing 51666*lambda1/2 into the Command Window.

In the total irradiance plot, the zoom feature was used. However, a clearer picture of the two peaks and the dip between them is better shown by changing the range of the angle :