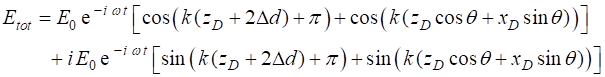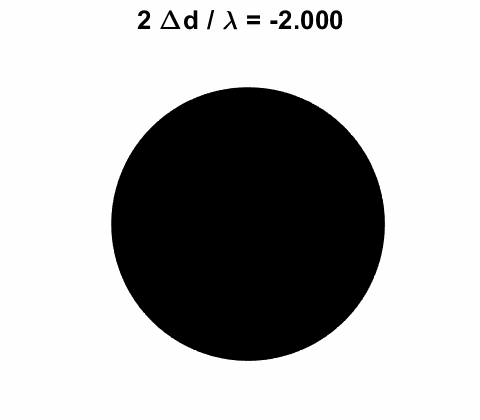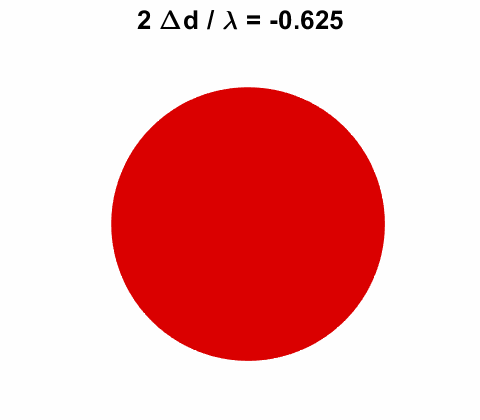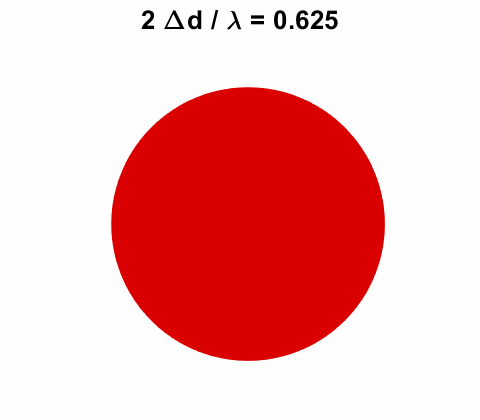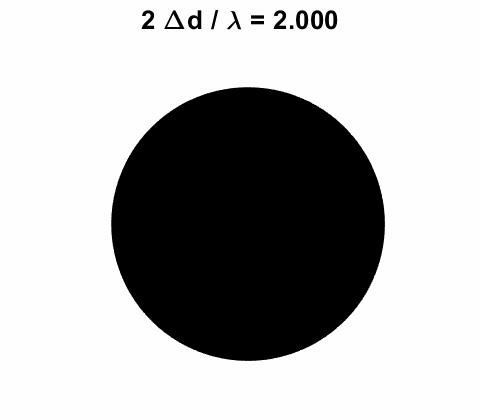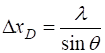DOING PHYSICS WITH MATLAB

 

MICHELSON INTERFEROMETER

Fringe Patterns

 

 

Ian Cooper

Email:  matlabvisualphysics@gmail.com

 

 

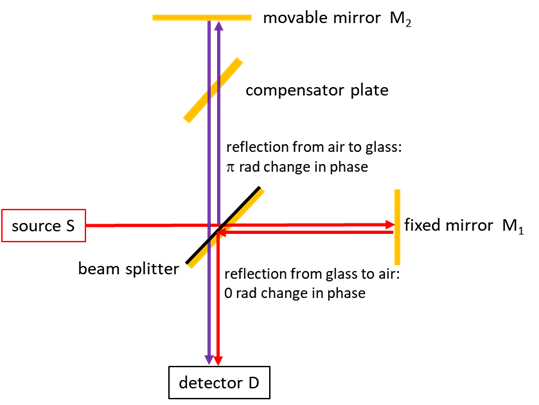
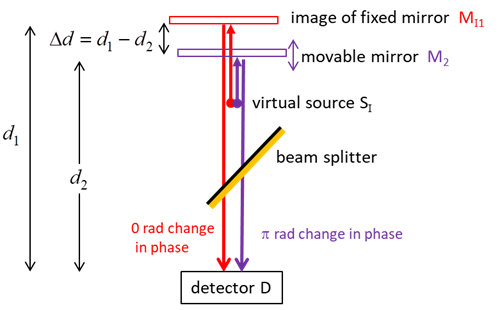
MATLAB SCRIPTS

 

MATLAB DOWN LOAD DIRECTORY

 

opMichA.m

Plane wave illumination of Michelson Interferometer. The mirrors are aligned perpendicular to the beam. An animation is displayed of the view on a detector screen as the distance between the mirrors is changes. The Michelson Interferometer can be used to measure small distance and an example of measuring plant growth is used. Calls the function ColorCode.m.

 

opMichB.m

Plane wave illumination of Michelson Interferometer with one of the mirrors tilted by a small angle w.r.t. the X axis. A vertical fringe pattern is shown on the detector screen. Calls the function ColorCode.m.

 

opMichC.m

Point source illumination of Michelson Interferometer produces circular fringes. Input parameters: wavelength and virtual source separation. Calls the function ColorCode.m.

 

 

MICHELSON INTERFEROMETER

 

In the Michelson interferometer, light from a source is split into two beams at a beam splitter (partially reflecting mirror). One beam travels to a fixed mirror M1 and is reflected back to the beam splitter while the other beam is reflected from a movable mirror M2 back to the beam splitter. The two beams recombine and are then detected as shown in figure 1.  The two beams must be mutually coherent for interference fringes to be observed.  This process is known as interference by division of amplitude. It is assumed that the beam splitter divides the two beams equally and is oriented at 45o to the source beam.

 

 

     Fig. 1.   Michelson interferometer.

 

When the two beams combine at the detector, there is a phase difference between them because of the phase change at the beam splitter for the beam reflected from mirror M2.

 

 

A linear optical equivalent of the Michelson interferometer helps to understand the optical path differences (figure 2). The mirror M1 is replaced with its virtual image M1I seen when looking into the beam splitter from the source. The source aperture is replaced by its virtual image SI as seen looking into the beam splitter from the position of mirror M2. The detected interference pattern is the same as would be generated by a source SI that is reflected from two distinct mirrors M2 and M1I, separated by a distance .

 

 

     Fig. 2.   Linear optical equivalent arrangement of the Michelson interferometer.

 

For the rays that travels along the central path of the interferometer, the optical path difference between the light reflected from the two mirrors M1I and M2 is .

At the centre of the detector

                 destructive interference – dark spot        

                 constructive interference – bright spot       

 

Illumination by a monochromatic plane wave

Assume the two mirrors M1I and M2 are illuminated by an incident plane wave. The mirror M2 is titled at an angle  with respect to the X axis as shown in figure 3. Let the Origin of the coordinate system be the centre of mirror M2. The waves are reflected normally by mirror M1I (wave 1) and at an angle  to the Z axis by mirror M2 (wave 2).

 

Fig. 3.   Illumination by monochromatic waves with mirror M2 titled at an angle  with respect to the X axis. Fringes of equal thickness are generated.

 

 

The electric fields for the two plane waves at the point  on the screen of the detector are

        (1A)    

        (1B)    

 

 

Then, the resultant electric field  at the detector is the superposition of the fields  and .                  

                   

                   

 

          (3)    

          

         

         

 

The intensity  of the combined beam at the detector screen is

         

 

and after much algebra

         

 

          (4)    

 

 

 

Mirrors precisely aligned at right angles to the beam

 

If the two mirrors are precisely parallel  as shown in figure 2, then the intensity on the screen is

         

 

and the whole area of the screen will be uniformly illuminated.

 

The screen will be dark when the difference in the optical path lengths of the two beams are an integral multiple of a wavelength and bright when the there is an odd multiple of a half-wavelength (figures 4 and 5).

 

      Dark (destructive interference)              

      Bright (constructive interference)          

 

 

Fig. 4.   The detector screen SD intensity as a function of the optical path length difference for the reflections from the two mirrors.

 

 

     Fig. 5.   Variation in the detector screen intensity as the position of mirror M2 changes.

 

Figure 5 shows that the number  of fringes that cross the centre of the detector screen when M2 is moved a distance is given by . 

 

 

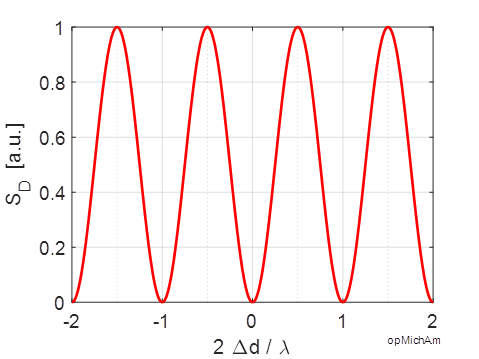
Example     Plant Growth

The Michelson interferometer can be used to measure small displacement accurately. For example, it is possible to measure the growth rate of a plant. The plant was attached to the movable mirror M2 and its position was adjusted to give a black field of view on the detector screen. A helium-neon laser was used with a wavelength 0f 632.8 nm. As the plant grew, the distance between the mirrors increased. So, the fringe pattern changed in a manner as observed in the animation of figure 5. In an 8.0 hour period,  dark fringes crossed the field of view. Estimate the growth rate of the plant in mm.h-1 and its uncertainty. 

 

The calculation can be done using the Script opMichA.m

% Plant Growth Calculation

% wavelength [m]

  wL = 632.8e-9;

% Time interval  [h]

  dt = 8;

% Number of fringes

  nf = 3420;

% distance moved by plant on mirror 2 [mm]

  dP = (nf * wL /2) * 1e3;

% rate of growth  [mm/h]

  dPdt = dP/dt;

 

  disp('Inputs  ')

  fprintf('   wavelength = %3.1e  m  \n',wL);

  fprintf('   time interval = %3.1f  h  \n',dt);

  fprintf('   fringes  = %3.0f    \n',nf);

  disp('Outputs  ')

  fprintf('   growth distance = %3.5f  mm  \n',dP);

  fprintf('   rate of growth  = %3.5f  mm/h  \n',dPdt);

 

 

Inputs 

   wavelength = 6.3e-07  m 

   time interval = 8.0  h 

   fringes  = 3410   

Outputs 

   growth distance = 1.07892  mm 

   rate of growth  = 0.13487  mm/h 

 

Inputs 

   fringes  = 3415   

Outputs 

   growth distance = 1.08051  mm 

   rate of growth  = 0.13506  mm/h 

 

Inputs 

   fringes  = 3420   

Outputs 

   growth distance = 1.08209  mm 

   rate of growth  = 0.13526  mm/h 

 

Growth rate  =   mm.h-1

 

 

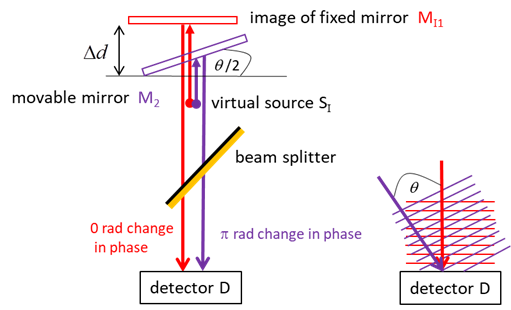
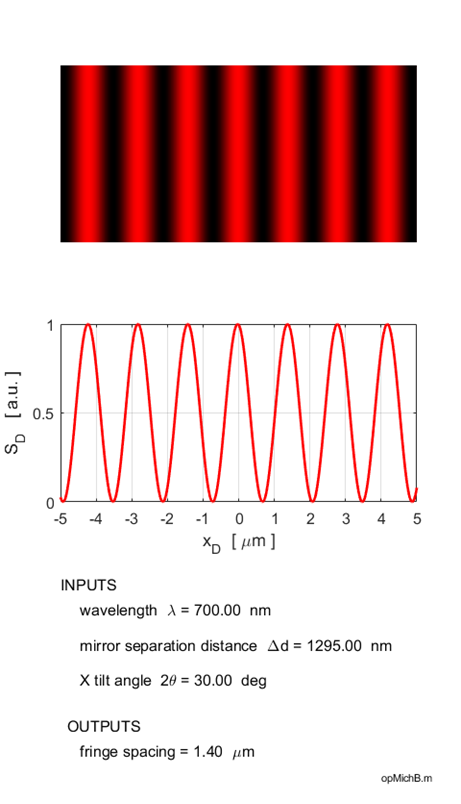
Mirror M2 rotated about the Y axis

     Waves reflected by M2 at an angle  to the Z axis

 

The intensity of the detector screen is due to the interference of the two plane waves. The wavefronts from the reflection from mirror M­1I are parallel to the screen, while the wavefronts from the reflection from mirror M2 are tilted at an angle to the screen (figure 3).  The resultant interference pattern shows a series of vertical bright and dark equally spaced fringes. The angle  is the tilt of mirror M2 w.r.t. the X axis and is the angle of the plane wave from mirror M2 w.r.t. to the Z axis as shown in figure 3.

The fringes are given by the equation

     (4)    

 

Using equation 4, the spacing between two adjacent bright or dark fringes at positions  and  is given by equation 5, since a sine squared function has a period of  rad.

              

           

     (5)   

When

            

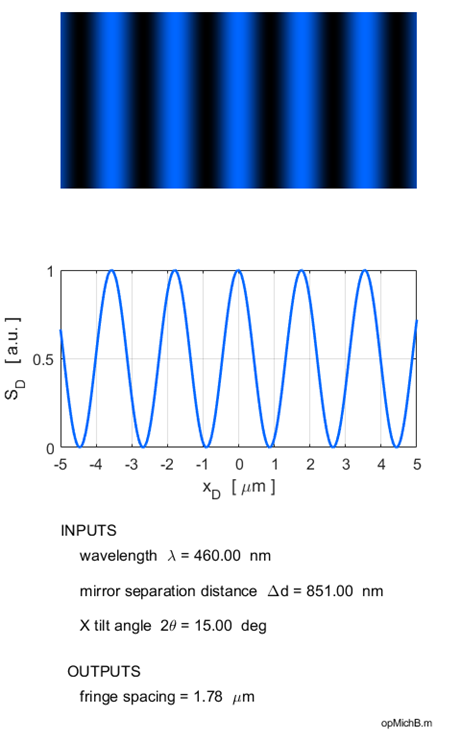
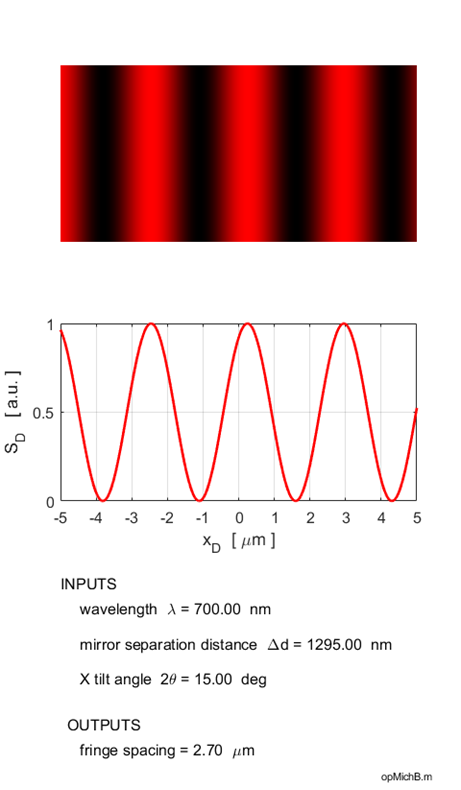
the fringes disappear and the screen becomes uniformly illuminated as described above.

The fringe separation becomes smaller as the wavelength decreases and the tilt angle becomes larger. When mirror M2 is moved, then the fringes move in a horizontal direction across the detector screen.

 

The Michelson interferometer is modelled for plane wave illumination with the Script opMichB.m and the Live Editor Script opMichBLE.mlx. Using the Live Editor with the numeric sliders, one can change the wavelength, mirror separation distance and the tilt angle and immediately observe the changes in the interference pattern.

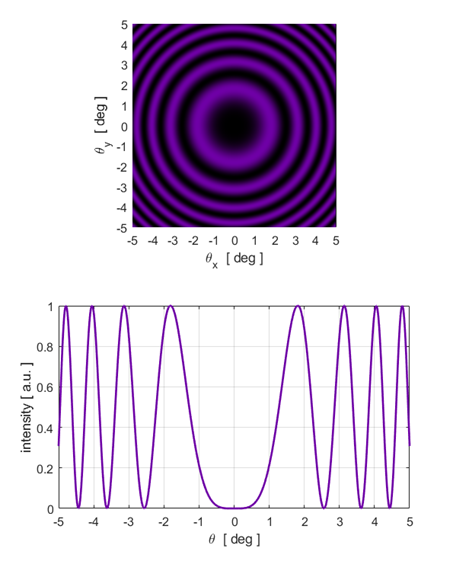
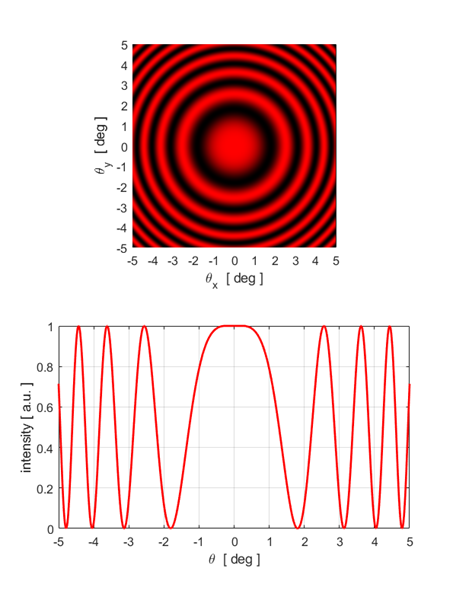
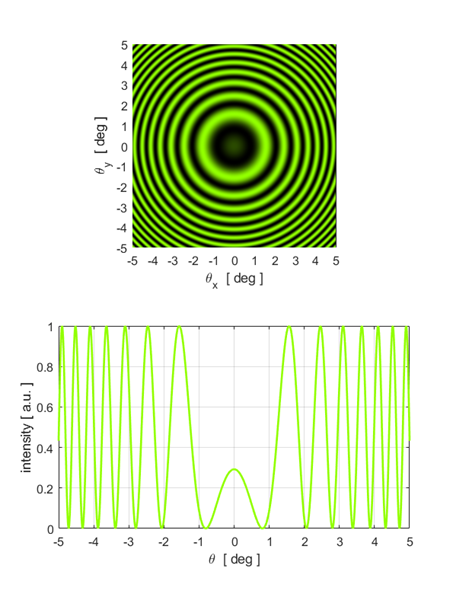
Fig. 6.   Fringes of equal thickness are generated when mirror M2 is tilted. The fringe spacing is reduced as the wavelength is decreased and the tilt angle is increased as predicted by equation 5.

 

 

 

Illumination by a monochromatic point source

You can calculate the fringe pattern for point source illumination using the script opMichC.m.

The input parameters are the wavelength, the distance between the virtual sources and the maximum viewing angle. The spherical waves produce circular fringes on a viewing screen.

 

A dark spot is located at the centre of the fringe pattern if the distance between the virtual source points

            

A bright spot is located at the centre of the fringe pattern if the distance between the virtual source points

            

m is called the order of the fringe.

 

Three examples are shown below.

 

     Fig. 7A.  Circular fringe pattern:

 

     Fig. 7B.  Circular fringe pattern:

 

     Fig. 7C.  Circular fringe pattern: