|
SIGNAL ANALYSIS ALIASING Sergio S Furuie email: sergio.furuie@usp.br Biomedical Engineering Laboratory Department of Telecommunication and Control School of Engineering, University of Sao Paulo, Brazil Ian Cooper Matlab
Script Download Directory Scripts by Serio Furuie oscAliasing.m oscAliasingAG.m (Script for saving animation as an animated gif file) Purpose To show
visually and graphically the concept of aliasing in signal processing. We are
using a rotating spot with frequency 1 Hz and measuring the y position y(t)
of its center. Therefore, y(t) is a sinusoidal signal with frequency f0
= 1 Hz. The image is sampled and refreshed at different frame rates fS, showing visually the effects of sampling.
The signal y(t) is sampled with same sampling frequency fS.
We also indicate, in frequency axis, the 1 Hz of signal and the Nyquist frequency fN,
which is half of frame rate fS. When aliasing occurs, we also indicate
the alias frequency fA, which is the
actual signal frequency that will be discretized. The alias frequency is a
"reflection" of signal frequency in relation to Nyquist frequency.
Note what happens when alias frequency is less, equal and larger that
2xNyquist frequency. In the latter case, the reflected frequency is negative
and then is again reflected in relation to frequency 0. Motivation When
discrete signal and image data is properly sampled, then some degradations
will be impossible to correct. One of these degradations is aliasing, due to
under-sampling or lack of analog filtering prior to sampling. Fundamentals Let Y(f)
be the Fourier transform of y(t). It can be proved [1] that sampling y(t),
with frequency fS, the resulting signal yp(t) has Fourier transform YP(f) that is a repetition of
a scaled Y(f) around multiples of fS: YP(f) = fS.sum{Y(f-k.fS)};
k = -inf:inf. Consider that Y(f) has
significant components in the interval [-fm;fm].
Thus, the right part of Y(f-0.fS) will
meet the left part of Y(f-1.fS)
at f = fS/2 when we increase fm.
The frequency fS/2 is called Nyquist frequency of the discrete system. Any component
beyond Nyquist frequency will overlap with other shifts of Y(f). In this
case, even if we filter in the band [-fS/2;
fS/2] the signal cannot be recovered.
The Nyquist-Shannon sampling theorem says that if the highest meaningful
component frequency of y(t) is fm, then
the sampling frequency should be at least 2.fm. References 1. Alan V. Oppenheim, Alan S. Willsky, S. Hamid, Signals
and Systems, Pearson, ISBN-13: 978-0138147570
Explorations Input
signal: sinusoidal function Input signal frequency f0
= 1.0 Hz Sampling frequency fS
Nyquist frequency = Sampling frequency /
2 Aliasing frequency fA
if fN > f0
fA = | 2 fN – f0 | [case 1: redundant] Nyquist
freq >> Signal freq fS
= 8 Hz fN
= 4 Hz Signal can be fully
reconstructed The motion of Spot
is smooth [case 2: fair] Nyquist
freq > Signal freq fS
= 3 Hz fN = 1.5 Hz Signal
reconstruction reasonable The Spot jumps from
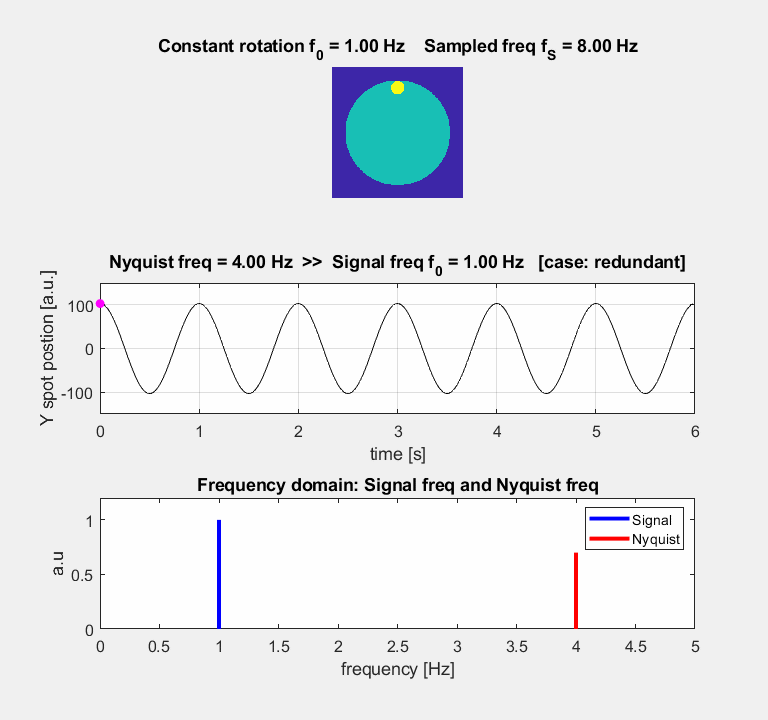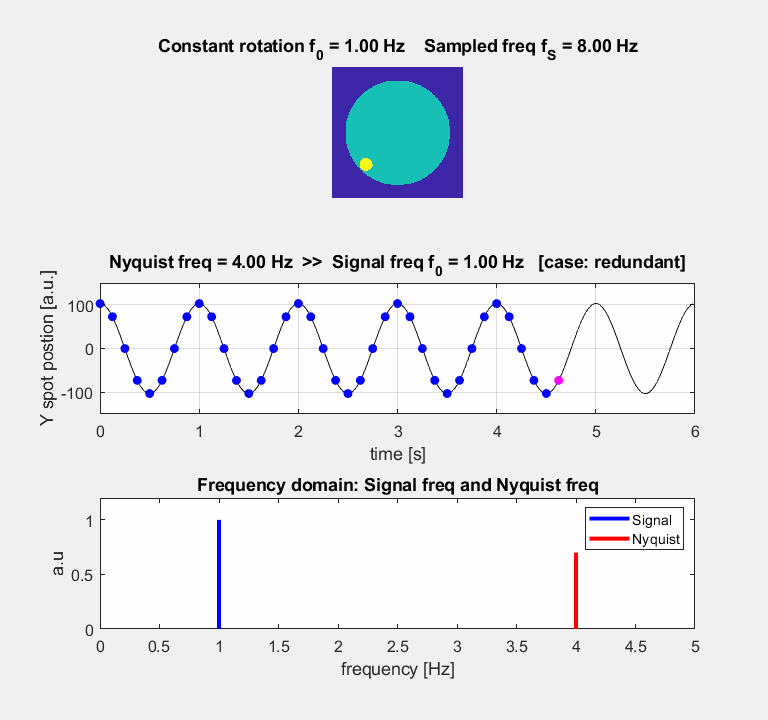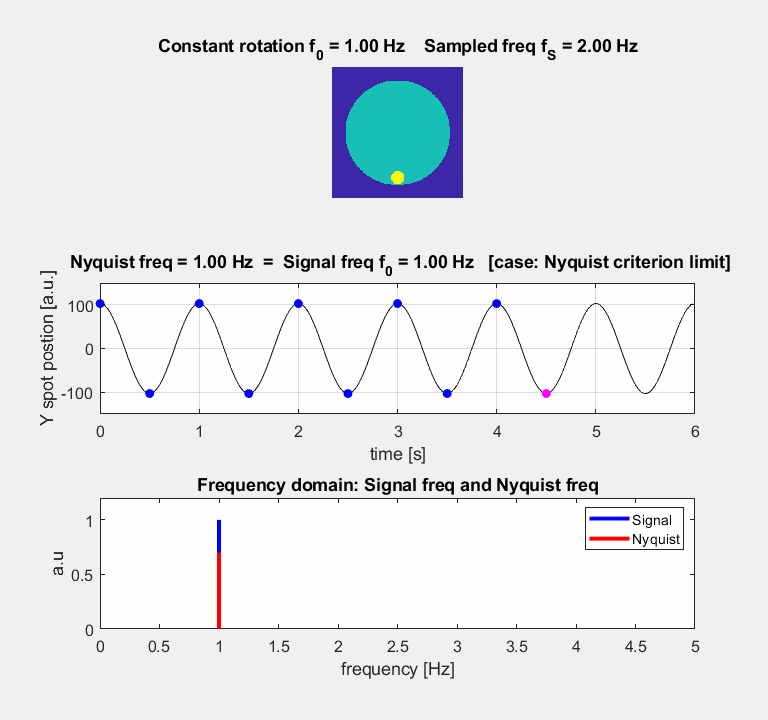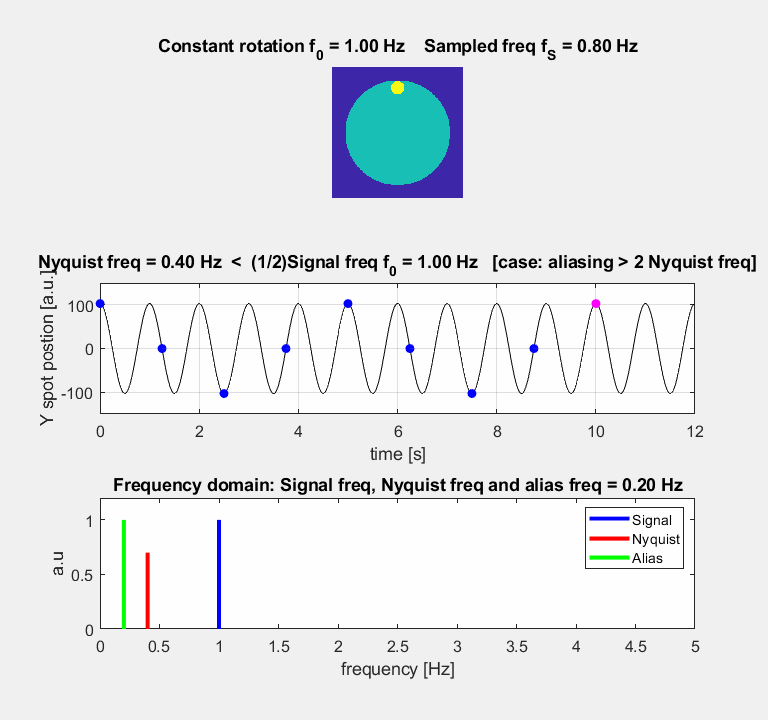
place to place [case 3: Nyquist criterion limit] Nyquist
freq = Signal freq fS
= 2 Hz fN = 1 Hz Signal cannot be
reconstructed The Spot jumps
between its extreme positions [case 4: aliasing < 2 Nyquist
freq]
Nyquist freq <
Signal freq fS = 1.2 Hz fN
= 0.6 Hz fA = 0.2 Hz Signal cannot be
reconstructed: aliasing produced A low frequency
component is now present at 0.2 Hz (graph: TA = 5.0 s) Stroboscopic effect:
The Spot rotates in the opposite sense (wagon wheel effect) [case 5: aliasing = 2 Nyquist
freq]
Nyquist freq =
(1/2) Signal freq fS
= 1 Hz fN = 0.5 Hz fA
= 0 Hz Signal cannot be
reconstructed: aliasing produced A low frequency
component is now present at 0 Hz Stroboscopic effect:
The Spot’s position is frozen [case 6: aliasing > 2 Nyquist
freq]
Nyquist freq <
(1/2) Signal freq fS = 0.8 Hz fN
= 0.4 Hz fA = 0.2 Hz Signal cannot be
reconstructed: aliasing produced A low frequency
component is now present at 0.2 Hz (graph: TA = 5.0 s) The Spot’s
position jumps about Aliasing: a pitfall of discrete sampling Usually in practice, one deals with data that
are sampled at discrete intervals. This may lead to the introduction of
erroneous results. If a component is present whose frequency is more than half the sampling frequency, it will appear
in the analysis at a lower frequency. This is the familiar stroboscopic
effect in which the wheels of the stagecoach appear to rotate backward
because the samples (movie frames) are not made rapidly enough. In signal
analysis, this is called aliasing. In Fourier analysis, N samples in time T allow the determination of unique Fourier coefficients only for the terms from k = 0 to n = (N−1)/2.
This means that for a sampling interval T/N, the maximum frequency is fmax = (N−1) f0/2 where f0
is first harmonic or f0 = 1/T. The period of the highest frequency
that can be determined is Tmin = 2T/(N−1).
This is approximately twice the spacing of the data points. One must sample
at least twice per period to determine the coefficient at a particular
frequency. Sampling frequency fS Nyguist frequency fN = fS / 2 The Nyquist Sampling Theorem states that: A bandlimited continuous-time signal can be sampled and perfectly reconstructed from its samples if the waveform is sampled over twice as fast as its highest frequency component fmax. For a bandlimited signal (one with a frequency spectrum that lies between 0 and fmax to be reconstructed fully, it must be sampled at a rate of fS > 2fmax (fN > fmax), called the Nyquist frequency. Half the sampling rate, i.e. the highest frequency component which can be accurately represented, is referred to as the Nyquist limit. No information is lost if a signal is sampled above the Nyquist frequency, and no additional information is gained by sampling faster than this rate. |