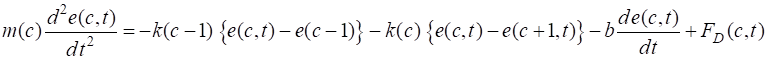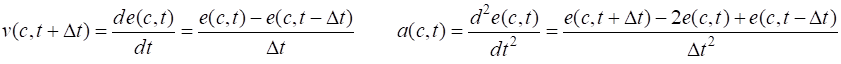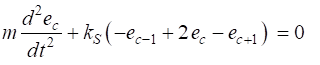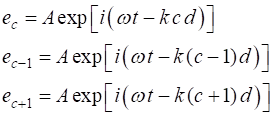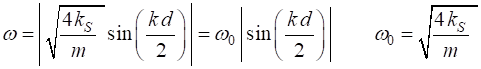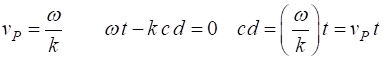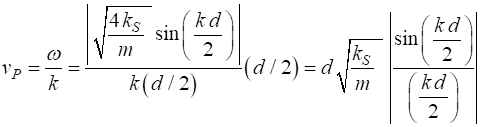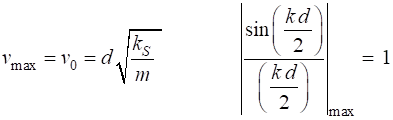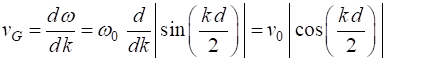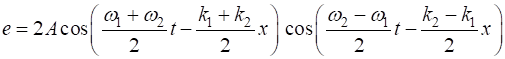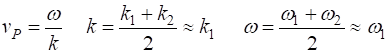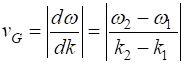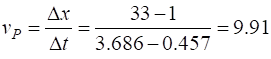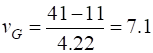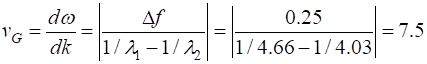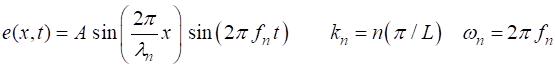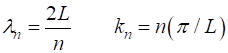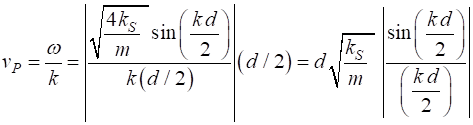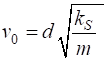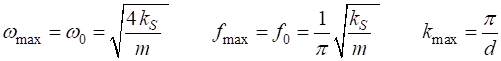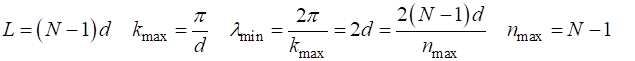DOING PHYSICS WITH MATLAB

 

COUPLED OSCILLATORS

     PART 3:   N-COUPLED OSCILLATORS

                   Wave Motion on a [1D] Atomic Lattice

                       

 

MATLAB SCRIPTS

Matlab Download Directory

 

oscC00NB.m

Plots of the dispersion relationships for a monatomic linear lattice as a function of the propagation constant for the angular velocity, phase velocity and group velocity.

 

oscC00NC.m

You can use the Script to explore the propagation along a [1D] atomic lattice for two sinusoidal wave trains and the superimposed wave train. The displacements of the atoms are calculated from analytical expressions. All parameters are changed with the Script. The animation can be saved as an animated gif file.

 

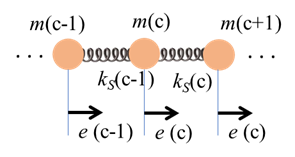
oscC00ND.m

A [1D] atomic lattice of N atoms is exciting by driving the displacement of atom 1 by either a single sinusoidal signal or the superposition of two sinusoidal signals. The equation of motions for the atoms are solved using a finite difference method to find the displacement of each atom as a function of time. You can investigate the frequency, phase velocity and group velocity as functions of the propagation constants as the signal propagates through the dispersive medium. All parameters are changed with the Script. The animation can be saved as an animated gif file.

 

oscC00NE.m

Explore the natural frequencies of vibration of an atomic lattice of N atoms long a [1D] chain. The system is excited by an external driving force that acts on an atom (an atom located at the location of an antinode is best). The equation of motions for the atoms are solved using a finite difference method to find the displacement of each atom as a function of time. The animation can be saved as an animated gif file.

 

You will need to download the Script simpson1d.m. This Script is used to evaluate a [1D] integral to calculate the Fourier Transform of a signal. The input array to the function must have an odd number of elements

 

 

INTRODUCTION

 

We will investigate the longitudinal vibrational motion of a [1D] chain of N atoms which are bound to one another by linear elastic forces (figure 1).

 

Fig. 1.   Geometry of the linear lattice. The equilibrium separation distance between atoms is d. The mass of the cth atom is  and the spring constant of the cth spring is  

 

It is assumed that the forces between neighbouring atoms are Hooke’s law forces, as if the atoms were bound together by massless ideal springs. At equilibrium, the atoms are situated on equally spaced sites with a separation distance d. When the chain of atoms is disturbed, the atoms may execute periodic motion about their equilibrium positions. The displacement of the cth atom from its equilibrium position at time t is given by the displacmenet .

 

The elastic restoring force  due to the springs acting on atom c at time t is determined by the extension or compression of the adjacent springs.

      (1)    

 

We will assume also that a damping force  proportional to the velocity (b damping constant) and a driving force  also act atom c. So, the equation of the motion for the cth atom is given by

     (2)              

 

 

We approximate the velocity and acceleration of atom c using a finite difference scheme

      (3)      

 

 

We can use equation 2 and equations 3 to calculate the displacement e from equilibrium at each successive time step . The displacement is given by the array e(row,column) where the row number gives the atom and the column is for the time step.

 

The code used for the implementation of the finite difference method is

 

KS = dt^2.*k;   Kb = b*dt;   KD = dt^2;  

for nt = 1 : Nt-2

  for c = 2 : N-1

    e(c,nt+2) = 2*e(c,nt+1) - e(c,nt)...

                -(KS(c-1)/m(c)) * (e(c,nt+1) - e(c-1,nt+1)) ...

                -(KS(c)/m(c))   * (e(c,nt+1) - e(c+1,nt+1)) ...  

                - (Kb/m(c))     * (e(c,nt+1) - e(c,nt))     ...

                + (KD/m(c))     * FD(c,nt+1);

  end

end

 

 

The displacement at time step nt+2 depends on the displacement at the two previous time steps. Therefore, to start the calculations, it is necessary to specify the displacement and velocity of the atoms at the first two-time steps.  For example, atom 2 starts with a displacement of 5 and zero velocity

   e(2,1) = 0.005;  e(2,2) = 0.005;

 

For a non-zero initial velocity for particle 2, the input is such that e(2,1)  e(2,2).

 

Arbitrary units are used for all quantities or you could use S.I. units.

 

For many of the simulations, for the motion along our chain of atoms, we can ignore the terms for the damping force and the driving force. An easy way to apply the driving force is simply to specify the displacements of individual atoms at each time step as shown in the code below, where atom 1 is driven by the superposition of two sinusoidal signals.

 

for nt = 1 : Nt-2

  for c = 2 : N-1

    e(1,nt+1) = A1*sin(w1*(nt+1)*dt) + A2*sin(w2 *(nt+1)*dt) ;

     

    e(c,nt+2) = 2*e(c,nt+1) - e(c,nt)...

                -KS * (e(c,nt+1) - e(c-1,nt+1)) ...

                -KS * (e(c,nt+1) - e(c+1,nt+1));               

  end

end

 

 

The component frequencies of the displacement from equilibrium for particle nE, can be found from its  Fourier Transform  by direct integration (not a fast Fourier Transform)

 

 

A wave propagates along the chain of atoms. We can estimate its wavelength by calculating the Fourier Transform of the displacements of all the atoms at a specified time step.

 

Hence, the estimates of frequency and wavelength means that we can calculate the phase velocity of a sinusoidal wave along the lattice .

 

 

% FOURIER TRANSFORMS ==================================================

 

% Frequency estimates fPeaks1 and fPeaks2

  fMin = 0.01;

  fMax = 5;

  Nf = 2901;

  H1 = zeros(1,Nf); H2 = H1;

  f = linspace(fMin,fMax,Nf);

  nE = ceil(N/2);

 

  for c = 1:Nf

    g = e(11,:) .*  exp(1i*2*pi*f(c)*t);

    H1(c) = simpson1d(g,0,tMax);

  end

 

  for c = 1:Nf

    g = e(41,:) .*  exp(1i*2*pi*f(c)*t);

    H2(c) = simpson1d(g,0,tMax);

  end

   

  PSD1 = 2.*conj(H1).*H1;

  PSD1 = PSD1./max(PSD1);

  [~, yy] = findpeaks(PSD1,f,'MinPeakProminence',0.6);

  fPeaks1 = yy;

 

  PSD2 = 2.*conj(H2).*H2;

  PSD2 = PSD2./max(PSD2);

  [~, yy] = findpeaks(PSD2,f,'MinPeakProminence',0.6);

  fPeaks2 = yy;

 

% Wavelength estimate lambda

  clear g

  H3 = zeros(1,Nf); lambda = linspace(2,20,Nf);

  xf = 0:40;

  fn = e(11:51,Nt)';

  for c = 1 : Nf

    g = fn .*  exp(1i*2*pi*xf/lambda(c));

    H3(c) = simpson1d(g,0,40);

  end

  PSD3 = 2.*conj(H3).*H3;

  PSD3 = PSD3./max(PSD3);

  [~, yy] = findpeaks(PSD3,lambda,'MinPeakProminence',0.6);

  wL_Peaks = yy;

 

% Propagation velocity: frequency x wavelength

  v = wL_Peaks * fPeaks1;

 

 

 

FREE MOTION OF THE ATOMS

 

Assuming the only force interactions between neighboring atoms are the elastic restoring forces, the equation of motion for the cth atom is

     (4)    

 

 

We want to find periodic solutions to the equation of motion, so we might expect the solution to have the form

     (5)    

 

 

where  is the angular frequency, is the propagation constant (not to be confused with the spring constant ) and position x is given by .

 

Substitution of equation 5 into equation 4 results in

    

                            

 

Hence,

     (6)    

 

 

The absolute values must be used, since the frequency is a positive quantity, regardless of whether k is positive or negative (wave moving to the right or left along the chain). The maximum angular velocity is .

 

Equation 5 gives solutions of the equation of motion (equation 4) provided that  is related to k by equation 6.  Equation 6 is called a dispersion relationship.

 

The phase velocity of a wave is the rate of advance of a point of constant phase along the direction of propagation. To determine the phase velocity, we may examine the motion of a point of constant phase. From equation 5, looking at a point of constant zero phase means that the phase velocity may be expressed as

     (7A)    

                

 

 

The maximum phase velocity is

         (7B)      

 

 

 

In general, a wave is a superposition of its harmonic components. The envelope or the group of waves are seen to move forward with a velocity  which is termed the group velocity .

     (8)    

 

 

It can be shown that the velocity with which the wave transmits energy along the propagation direction is the group velocity. In a wave train, no energy can ever be transmitted past a node, since the medium at the nodal point is motionless. Thus, the energy must be transmitted with the velocity with which the nodes themselves move, that is, the group velocity. For the case of standing waves, the group velocity is zero, and there is zero net energy flow in this case.

 

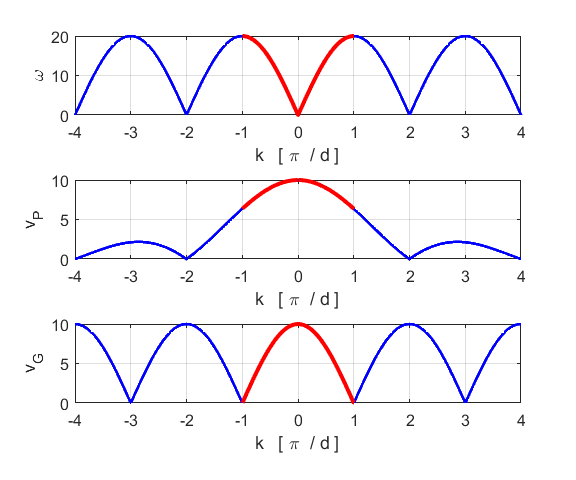
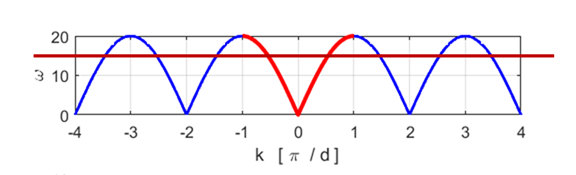
The dispersion relationship (equation 6), the phase velocity  (equation 7) and the group velocity  (equation 8) as functions of the propagation constant k for a linear monatomic lattice are shown in figure 2. Note that many values of k are be associated with any given frequency .

         Fig. 2.   Dispersion relationships for the monatomic lattice.  oscC00NB.m

 

From the plot of  and the dispersion relationship given by equation 6, if we restrict ourselves to values of the propagation constant k such that , and thus to values of the wavelength  which are much greater than twice the interatomic distance d, then  is approximately a linear function with k

     (6)    

 

In this long-wavelength limit, both the phase velocity  and the group velocity will be essentially constant

     (9A)                         long-wavelength limit

     (9B)    

 

For very long wavelengths, the dispersion effects are negligible and the medium acts like a continuous and homogeneous elastic medium. This is to be expected from a physical point of view, since for such long wavelengths, the atomic nature of the chain is of little importance as far as the dynamics of the system is concerned. As clearly shown in figure 2, as k increases, the dispersion effects become very important.

 

When

 

 

then the atoms cease to vibrate, and the wave cannot propagate along the lattice.

 

The phase velocity  when  

The group velocity  when  

 

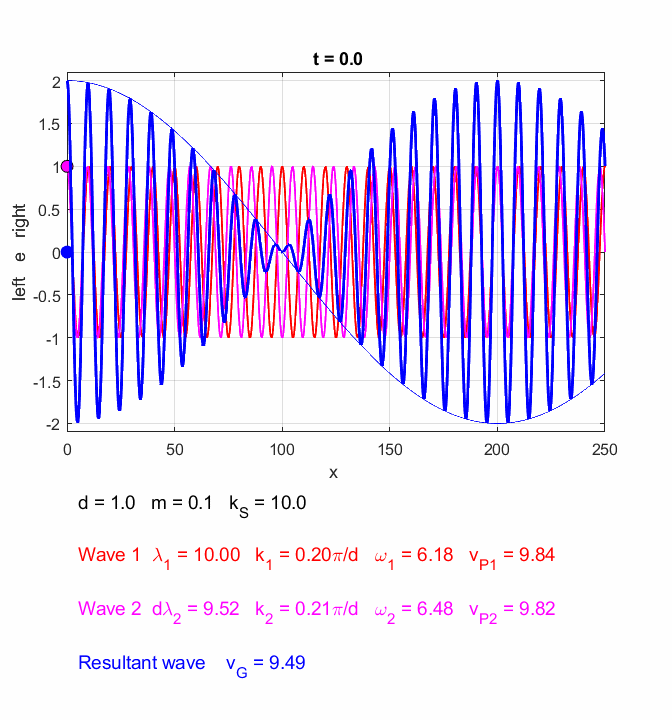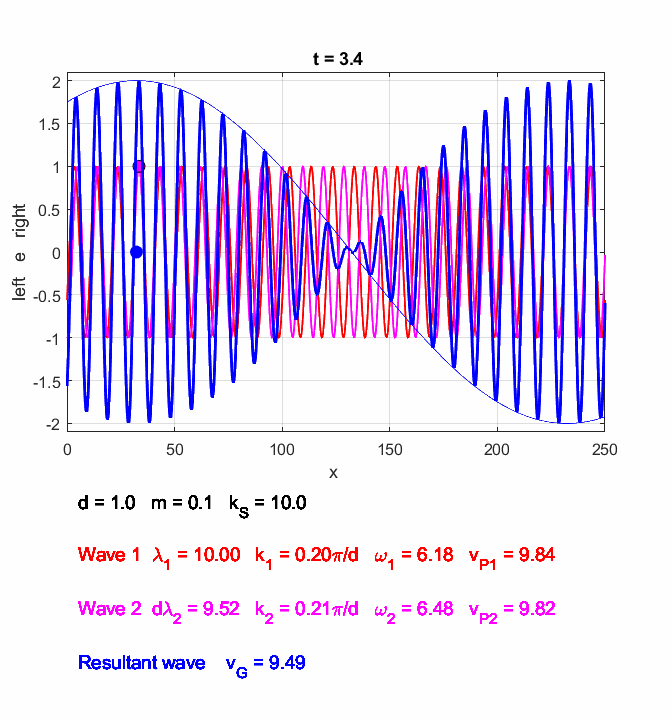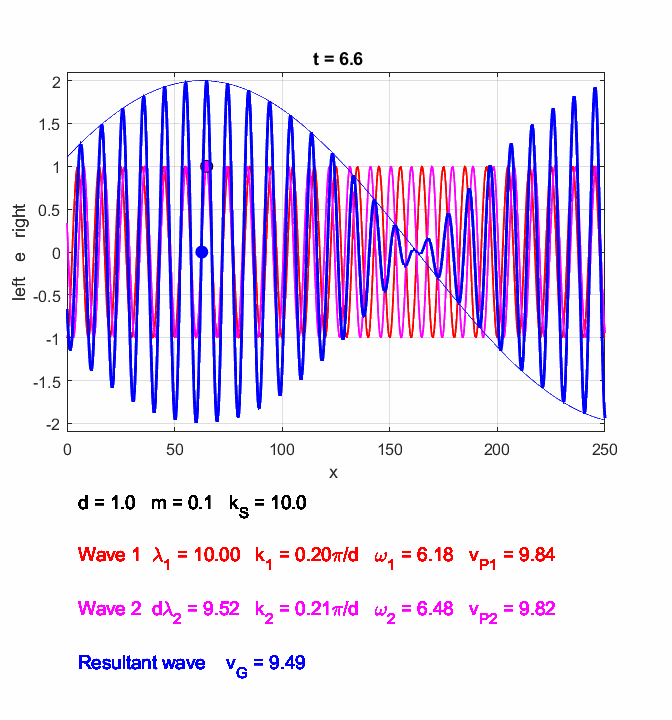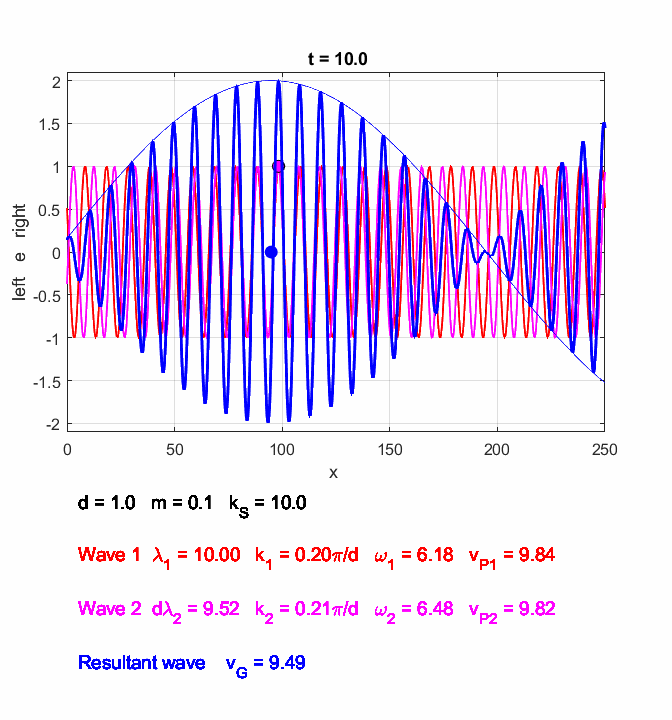
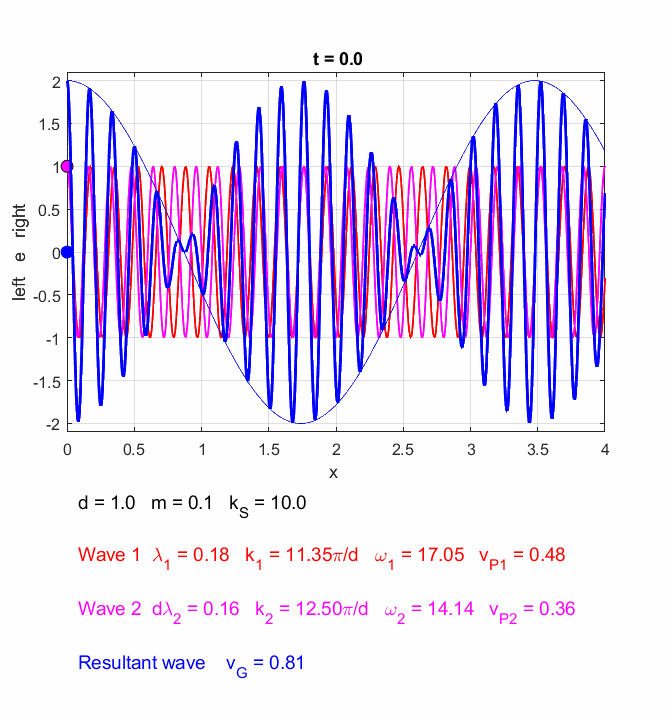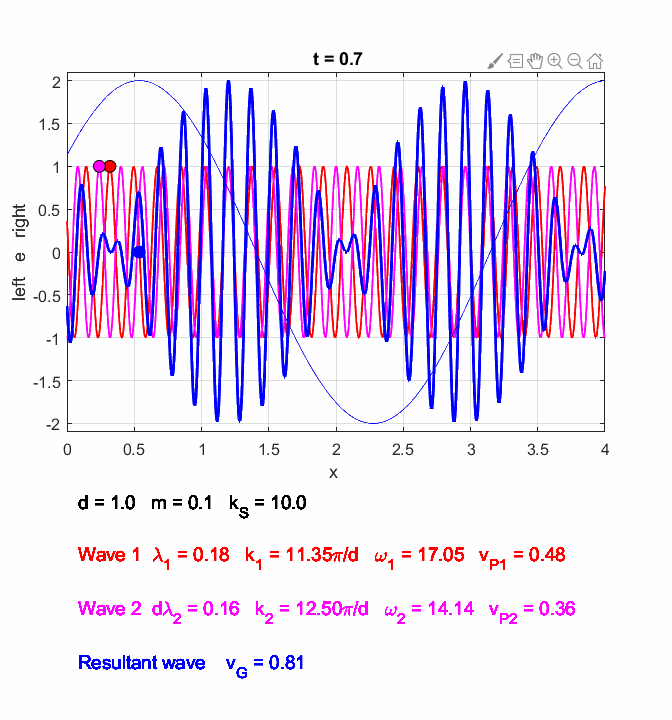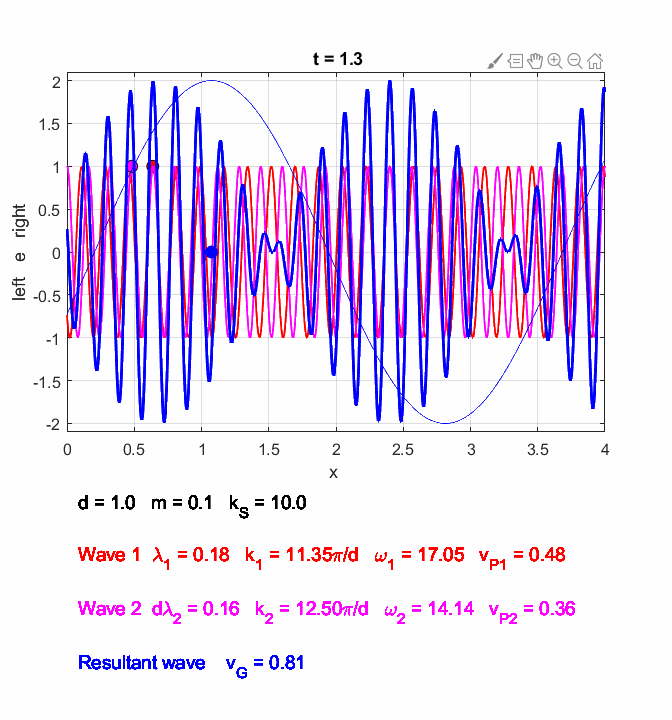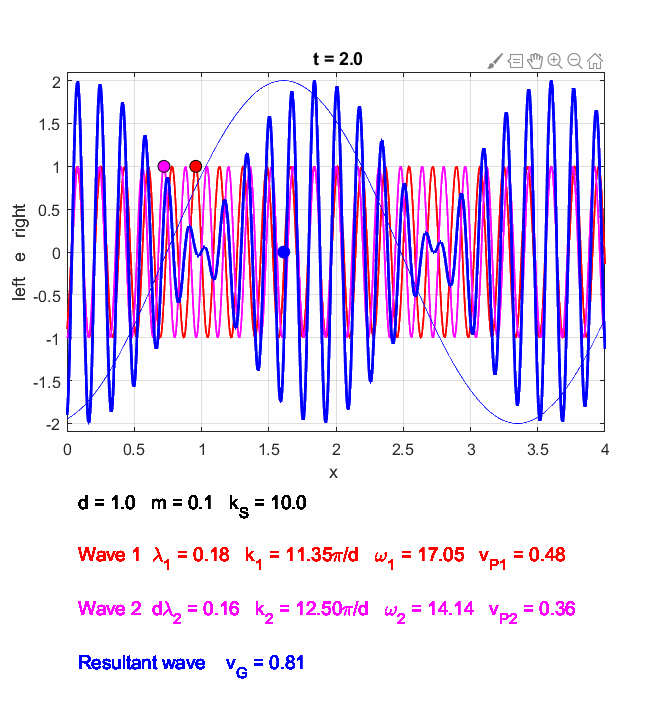
This gives the conditions for standing waves where the phase of the neighbouring atoms differ by radians.

 

 

Figure 3 to 6 shows the results of running the Script oscC00NB.m or oscC00NC.m with the input parameters: number of atoms N = 21, separation distance between atoms d = 1; mass of each atom m = 0.1, spring constant for each spring kS = 10.  (Note: all units are arbitrary)

 

 

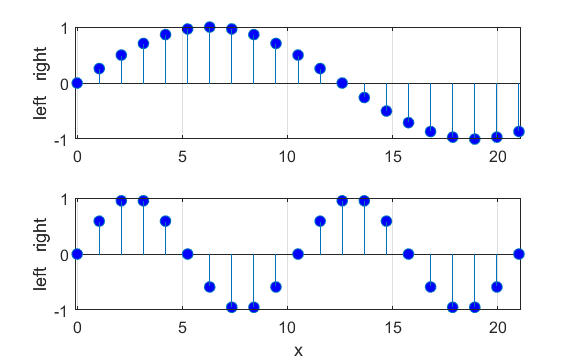
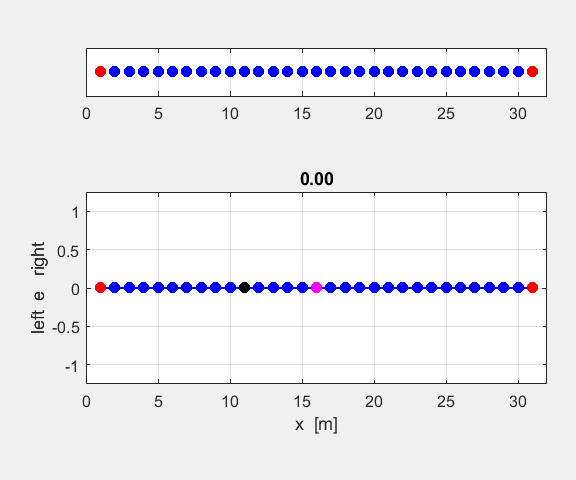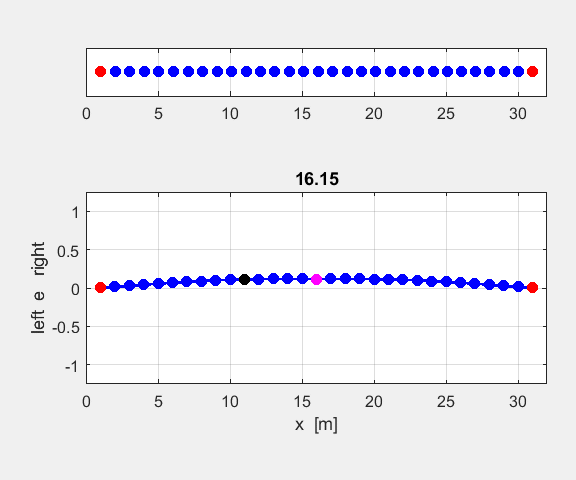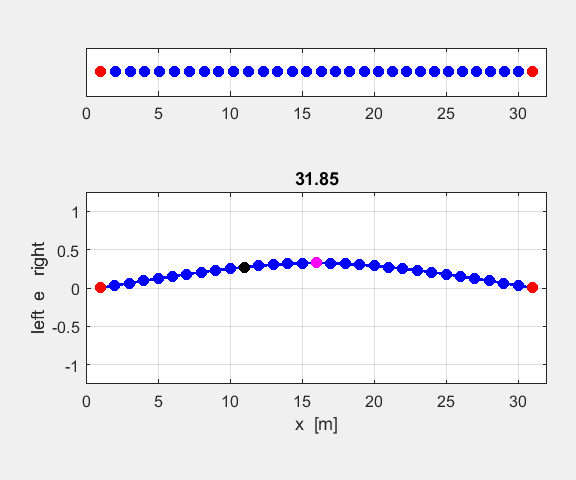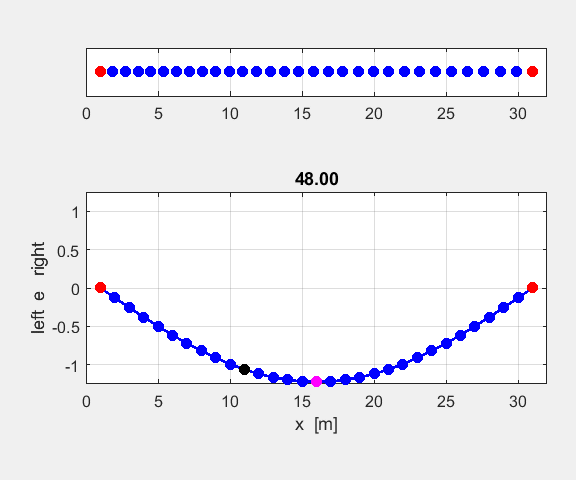
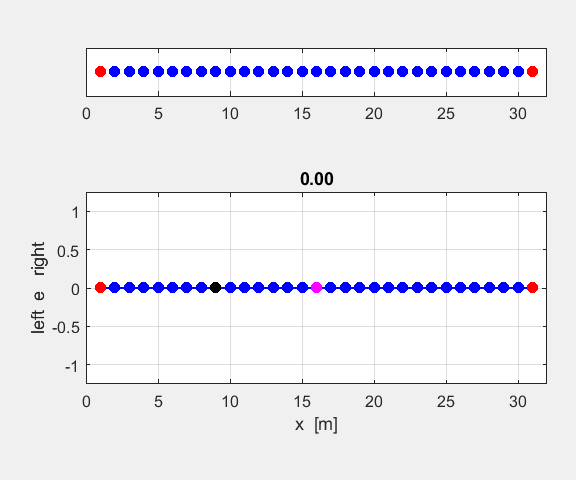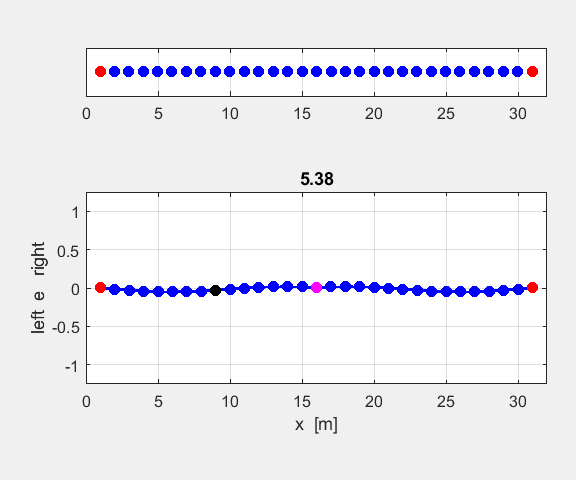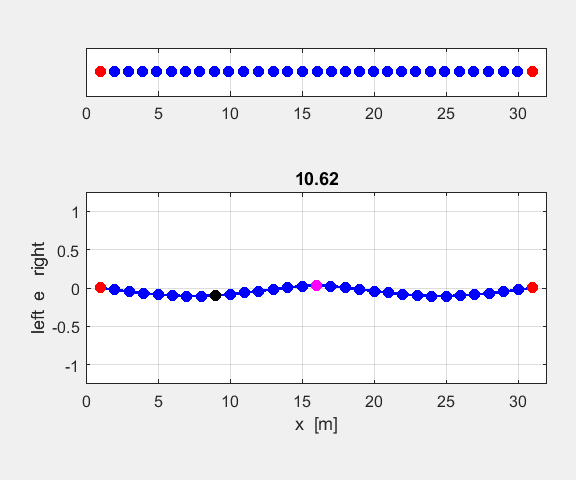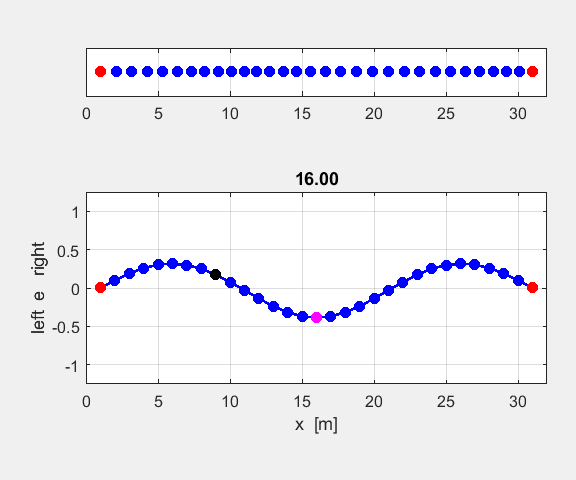
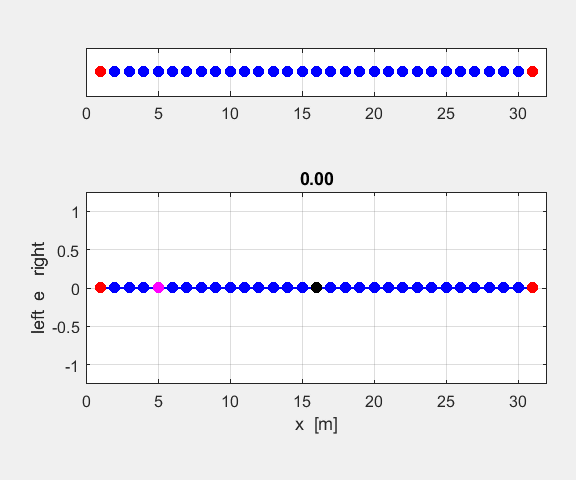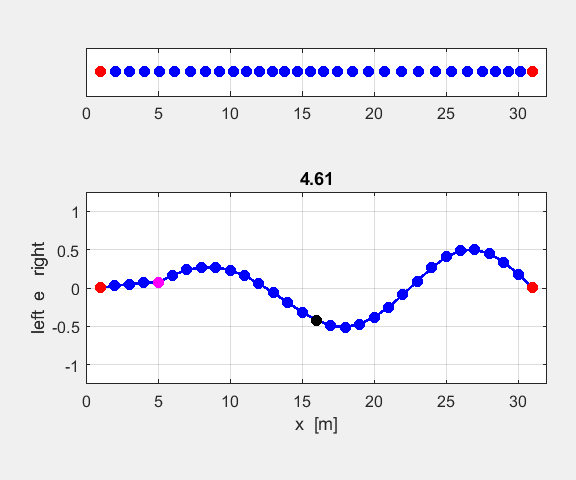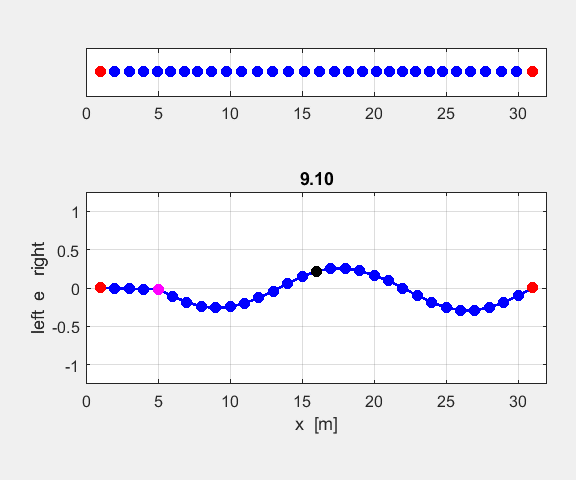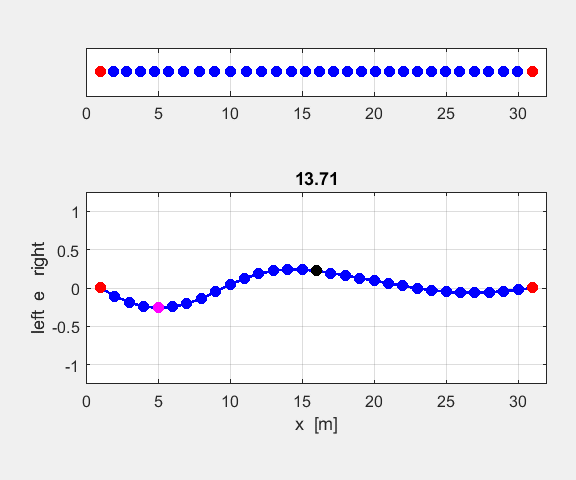
Figure 3 shows the atomic displacements on the monatomic lattice as transverse displacements for convenience of illustration (actual displacements are longitudinal ones in which the atoms are displaced along the chain, rather than normal to it).

Fig. 3.   Atomic displacements on the monatomic lattice for a long and short wavelength wave. The displacements are shown as transverse ones for sake of clarity. A positive displacement corresponds to a movement to the right and a negative displacement a movement to the left w.r.t. the equilibrium positions. oscC00NB.m

 

For any given value of k in the region  there will be a vibrational motion involving certain possible atomic displacements. However, as shown in figure 4, the same set of displacements of atoms associated with this wave, can also be associated with a wave of larger propagation constant k (smaller wavelength ) and with still another even larger k value.

 Fig. 4.   A single set of atomic displacements represented by two sinusoidal waves. oscC00NB.m

 

In other words, there are many representations of the same atomic displacement patterns, each involving different k values and hence different difference  values. These different representations must have the same value of angular frequency  (figure 5).

 Fig. 5.   Many values of propagation constant k may be associated with any given frequency .  oscC00NB.m

 

Thus, any possible arrangement of atomic positions which is compatible with a sinusoidal solution of any wavelength, however, short, can be presented as or reduced (translation by integer multiples of ) to a sinusoidal solution for which  and this belongs to the central zone. For this reason, it is not necessary in this case to consider vibrations other than those belong to the central zone . This central zone is called the first Brillouin Zone.

 

A pure sinusoidal signal can not transmit information. A sinusoidal wave propagates at a velocity equal to its phase velocity (equation 9A). So, we will now consider what happens when two wave trains of the same amplitude A , one of frequency  and propagation constant  and another of frequency   and propagation constant are superimposed.

    (10A)    

 

    (10B)    

 

If we assume  and  are small, then this superposition represents a wave characterized by the original values of  and multiplied by a sinusoidal envelope of much longer wavelength  called an envelope of beats.

 

The small wavelength wave propagates with phase velocity  

    (11)     

 

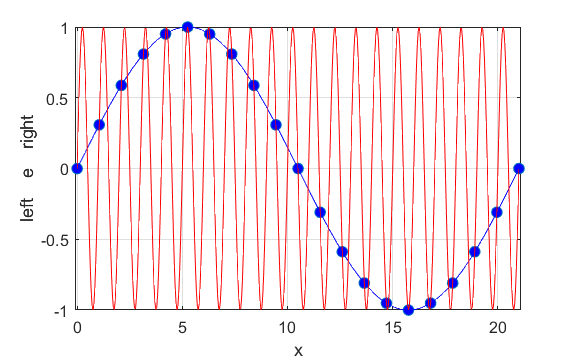
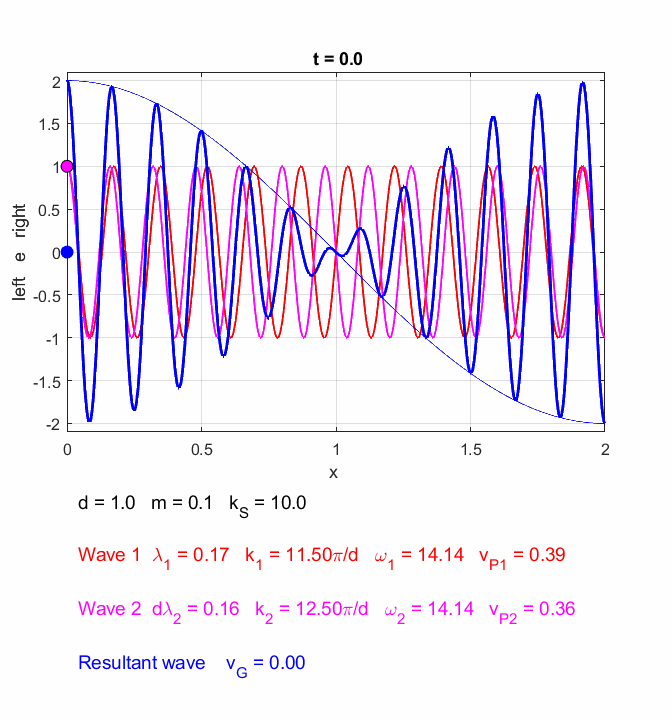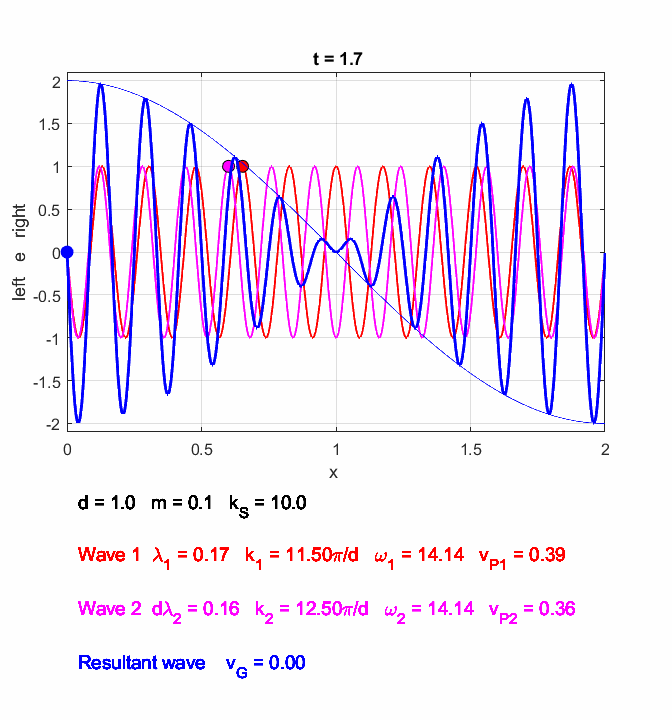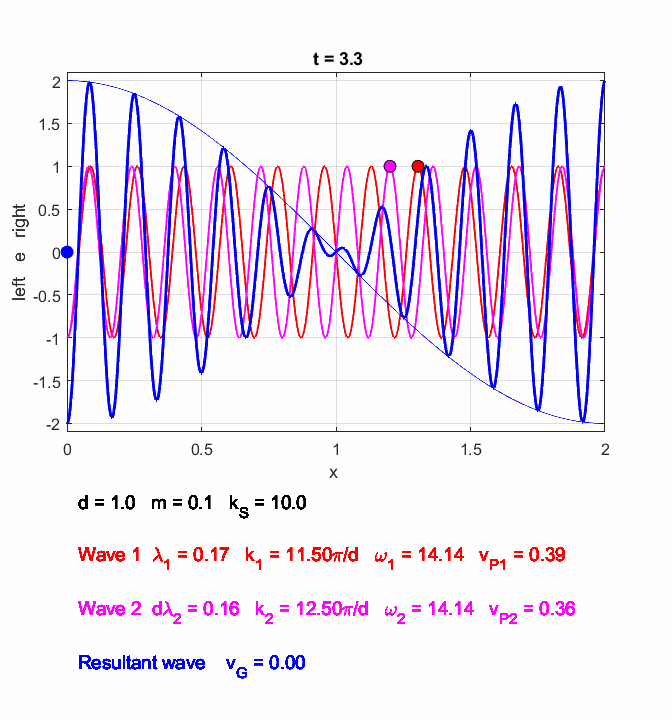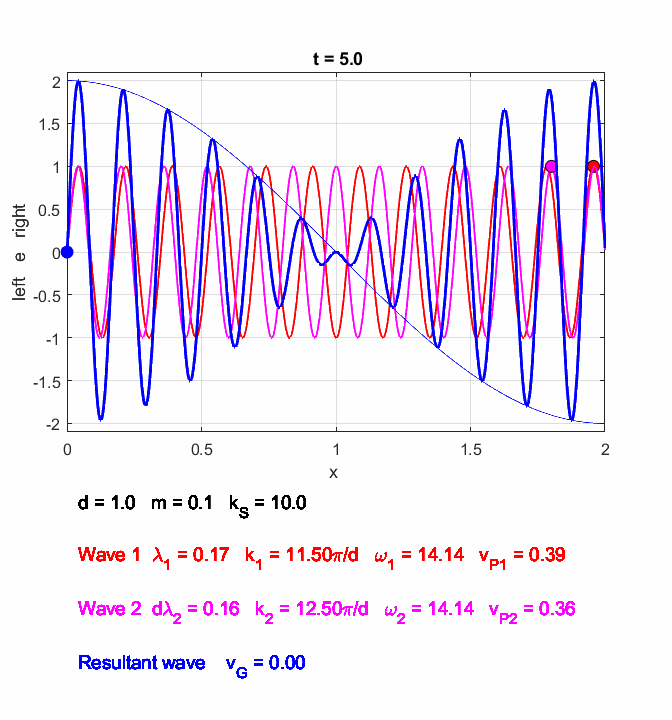
The phase velocity of the envelope corresponds to the group velocity  of the beats. Thus, the envelop propagates with this group velocity and it is this velocity with which the wave transmits energy along the propagation direction. 

    (10)     

 

 

You can use the Script oscC00NC.m to explore the propagation along the [1D] atomic lattice of the two sinusoidal wave trains and superimposed wave train.

 

 

If k <<  , then  and the dispersion effects are very small (figure 2). In this long wavelength limit, the phase velocity is essentially constant and is approximately equal to the value of the group velocity (figure 6).

Fig. 6.   In the long wavelength limit, the effects of the dispersion are small, and the two wave trains propagate at approximately the same speeds. The two wave trains have slightly different frequencies and the phase between the two waves continually changes so at once instance the two waves interfere constructively and a little later interfere destructively, producing the beat pattern. The beat pattern as shown by the envelope propagates at the group velocity (equation 10) which is approximately equal to the phase velocity of either wave train. The coloured dots help visualize the motion of the wave trains. oscC00NC.m

 

 

From equation 3 and figure 5,

       phase velocity  when  

we can conclude that the wave does not propagate as shown in figure 7.

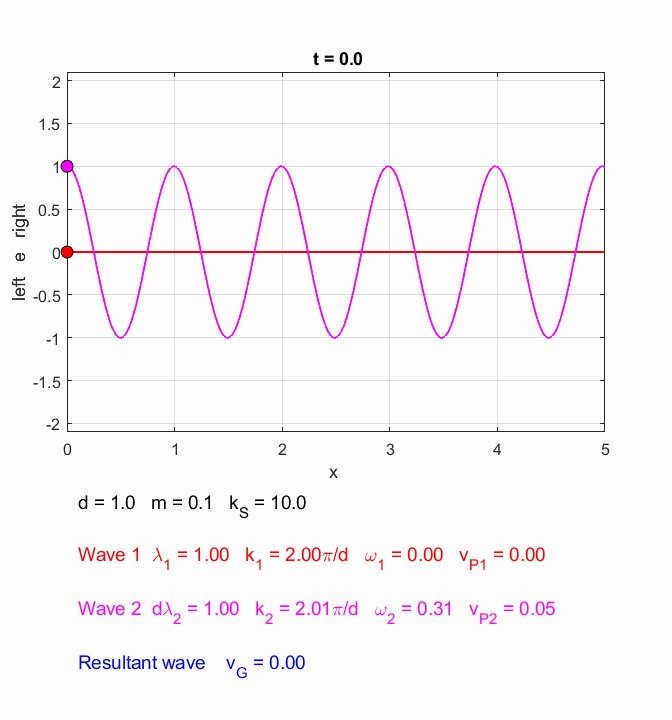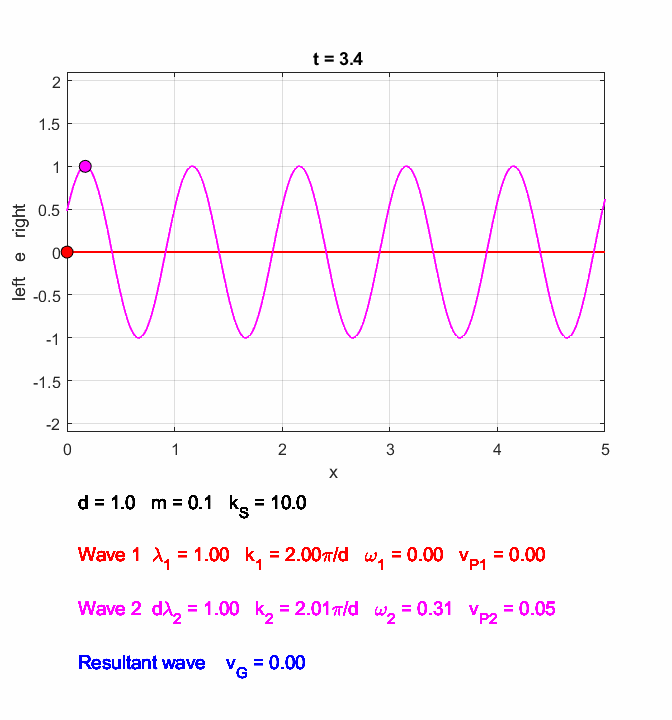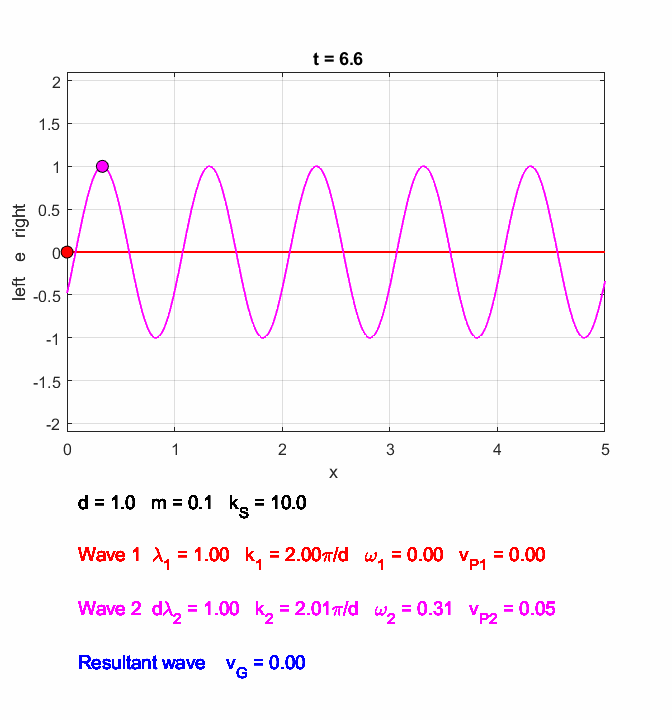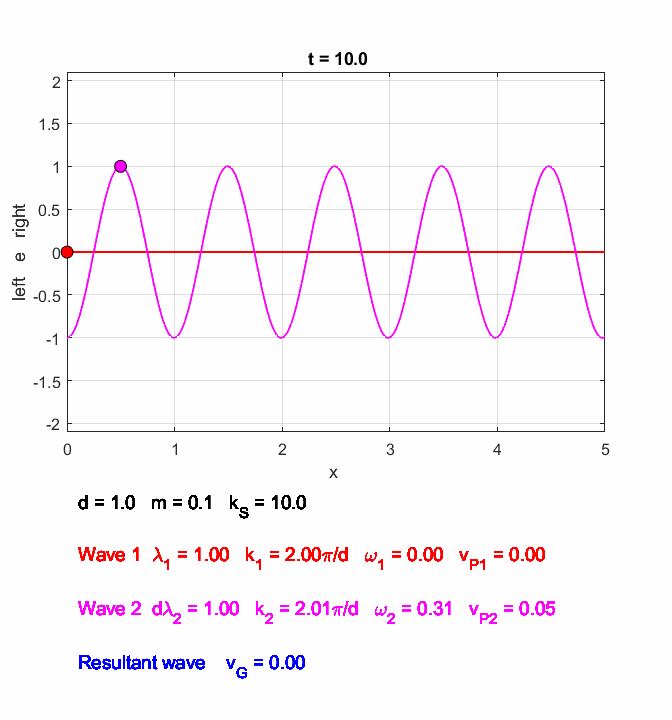
Fig. 7.  Due to dispersion effect, the when a sinusoidal wave has a propagation constant and wavelength such that   the atoms have zero vibrational frequency  and the wave does not propagate. Hence, wave 1 does not propagate. oscC00NC.m

 

An interesting example is shown in figure 8. The two waves have the same angular frequencies but different phase velocities. This results in zero group velocity of the superimposed wave, hence it does not propagate along the atomic lattice.

Fig. 8.   The two waves have the same angular frequencies but different phase velocities. This results in a zero group velocity of the superimposed wave. Hence, superimposed wave does not propagate along the atomic lattice. oscC00NC.m

 

The simulation in figure 9 gives mysterious results. The envelope propagates at the group velocity  but the motion of the envelope does not match the motion of the superimposed wave. It appears that a stationary wave is generated, and the wave is not propagated along the atomic lattice. A beat pattern is produced when the two waves have slightly different frequencies. As the phase between the waves continually changes, the wave become in phase and interfere constructively, later they are out of phase and interfere destructive giving the characteristic beat waveform. However, for the propagation in a dispersive medium, the two waves travel at different speeds and this also gives an additional phase change. In this instance, we get a beat pattern which does not appear to propagate at the predicted group velocity according to equation 9B. (Not too sure about this ???)

 

Fig. 9.  Due to dispersion effects, the superimposed wave does not propagate along the atomic lattice with a group velocity as predicted by equation 9B.  oscC00NC.m

 

 

But, I am not sure what all the above means!!!

Assume that an external force acts on the first atom on the left-hand end of the chain. By disturbing this atom, a wave will propagate along the chain to the right. The frequency of the vibrations will be determined by the external force, and the propagation speed by the elastic and inertial properties of the medium. Thus, the wavelength for the propagating wave and hence the propagation constant are determined by the driving frequency and medium. You cannot specify the propagation constant as indicated in figure 3 to give the frequency of vibration.

 

What do I think the above theory tells us!!!

For the input data with the Script oscC00ND.m: number of atoms N = 101, separation distance between atoms d = 1; mass of each atom m = 0.1, spring constant for each spring kS = 10.

(Note: all units are arbitrary)

The maximum phase velocity (equation 7) is .

The maximum frequency (equation 6) for a wave to propagate along the lattice is

                     

          

You can use the Script oscC00ND.m to investigate the propagation of a wave propagated along the lattice by exciting the motion of atom #1. The default excitation is the superposition of two sinusoidal signals

           e(1,nt+1) = A1*sin(w1*(nt+1)*dt) + A2*sin(w2 *(nt+1)*dt) ;

 

 

All parameters are changed within the Script. The variables f1 and df are used as the inputs for the angular frequencies w1 and w2.

      % INPUT: frequency f = 1 / frequency increment df = 0

      f1 = 1;

      df = 0;

  

   % INPUT: Amplitude A of waves 1 and 2  

     A1 = 0.5; A2 = 0.5;

 

   % Angular frequency w (omega) of waves 1 and 2 

     w1 = 2*pi*f1;

     f2 = f1 + df;

     w2 = 2*pi*f2;

 

 

Simulation #1    Propagation of a monochromatic wave     oscC00ND.m

 

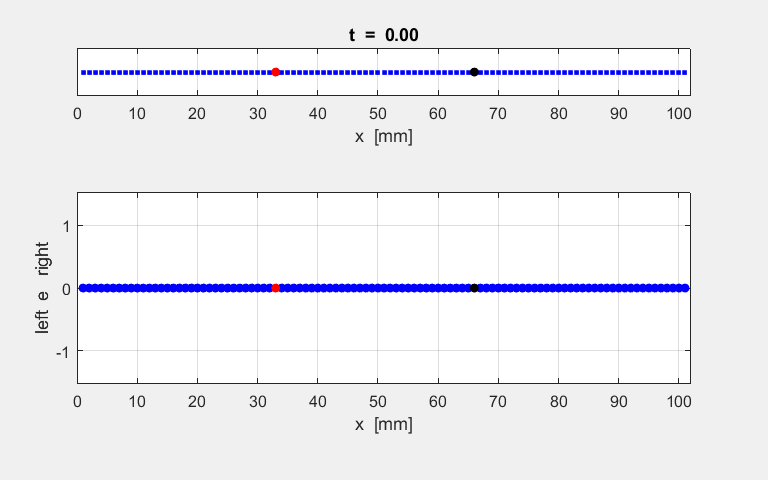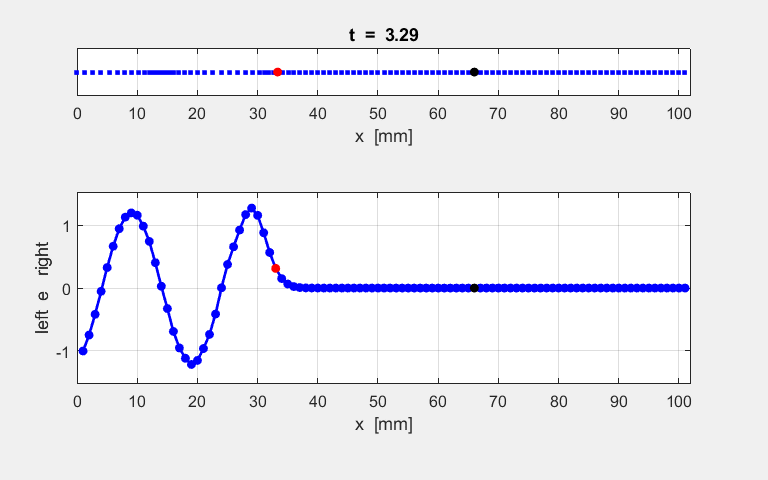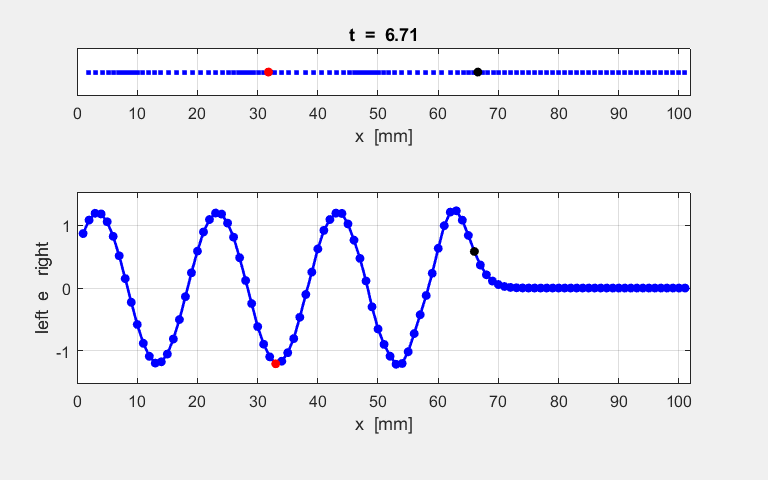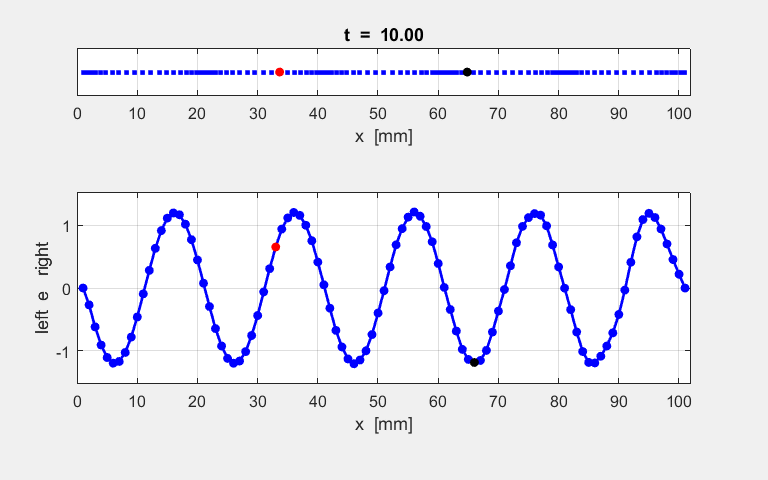
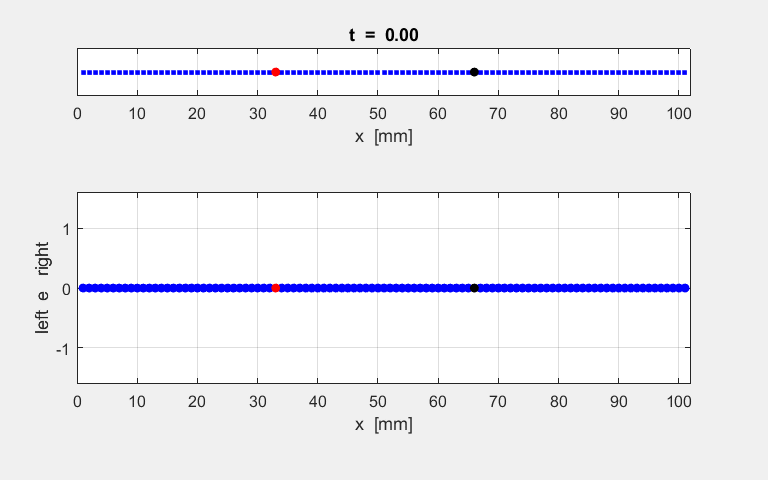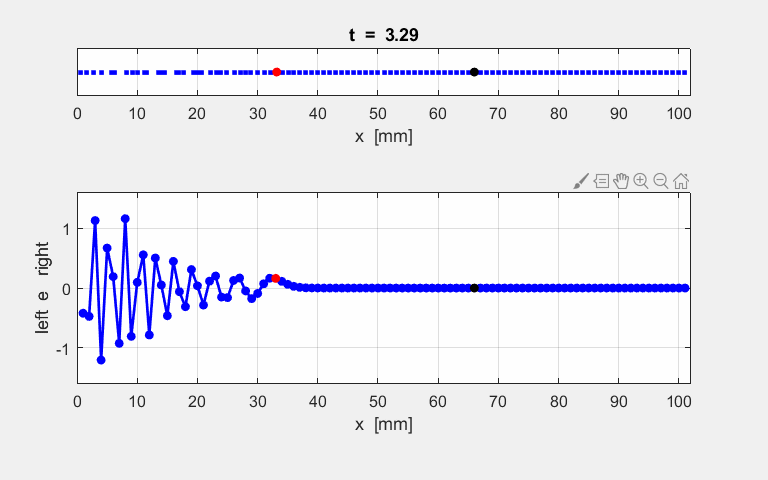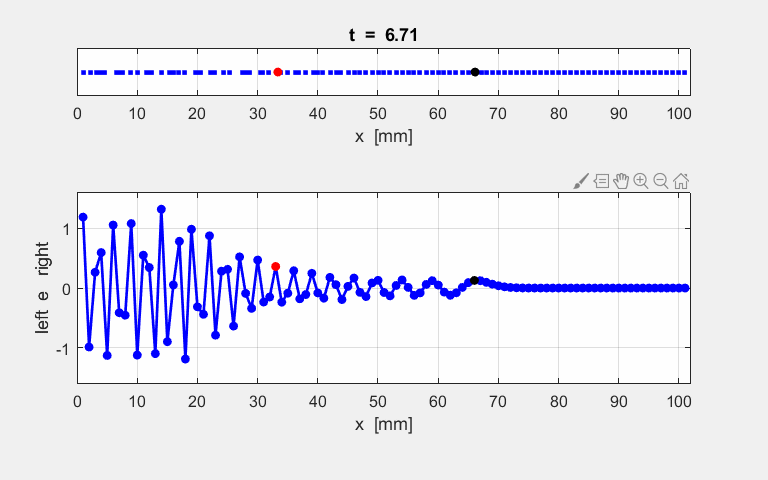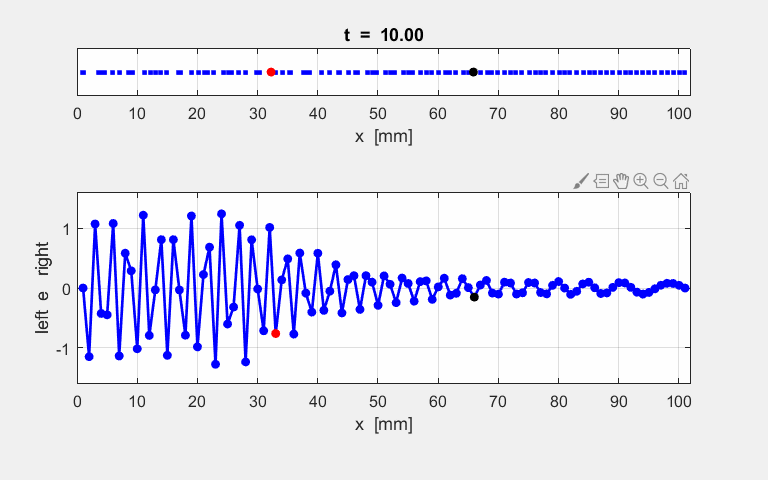
We can model the propagation of the monochromatic wave through our atomic lattice by driving the displacement of atom #1 by a sinusoidal signal of frequency f1. The model parameters are displayed in a Figure Window as shown in figure S1.

 

 

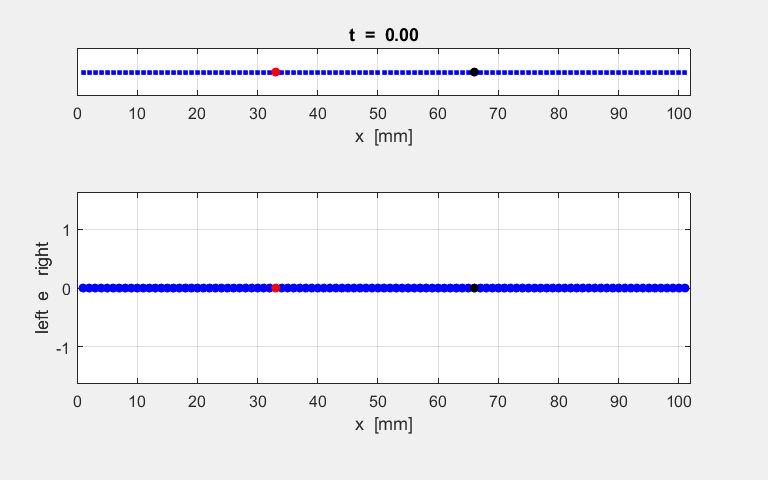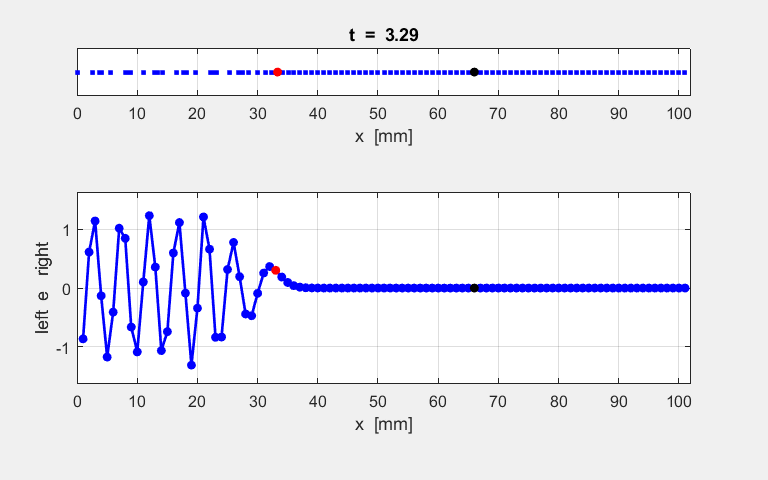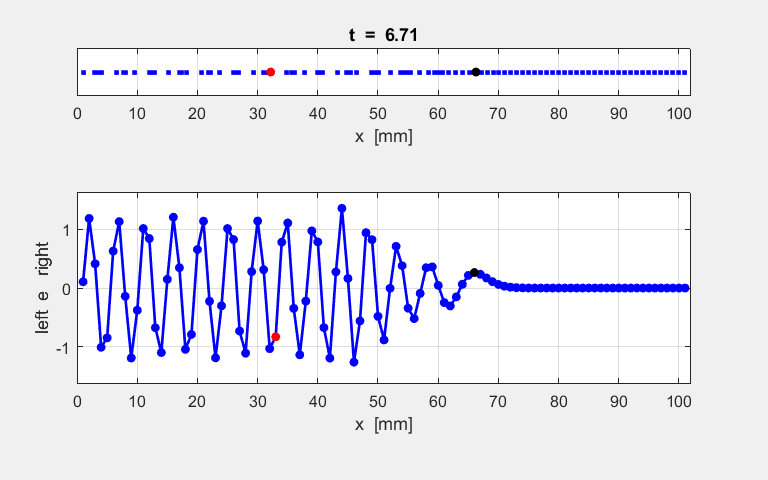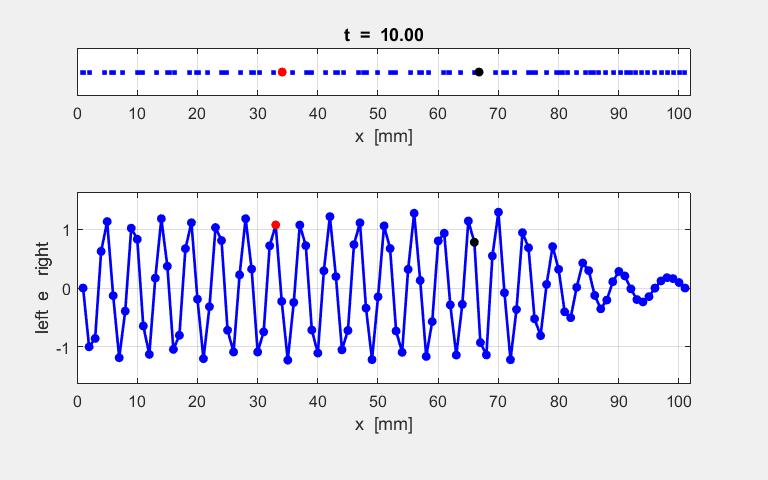
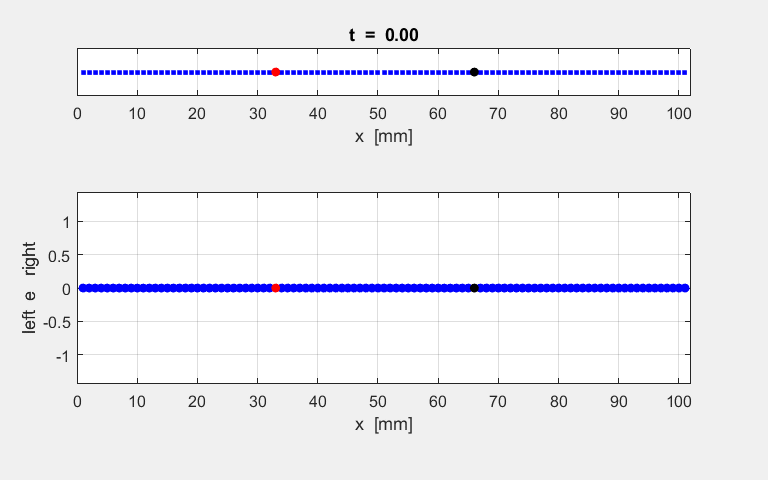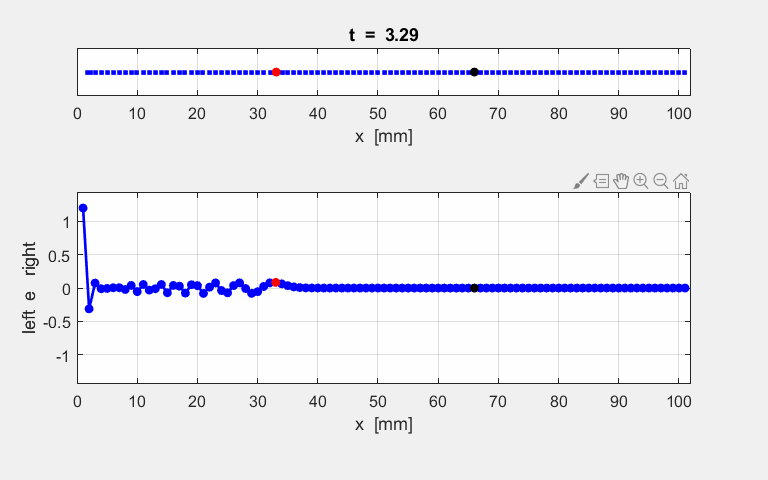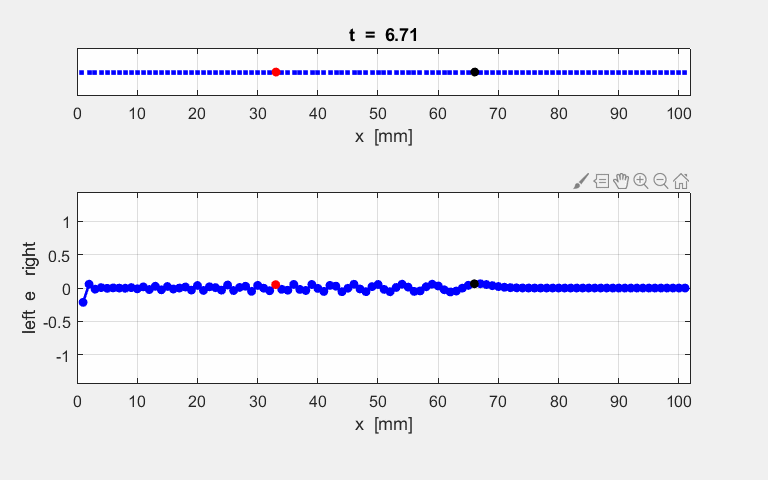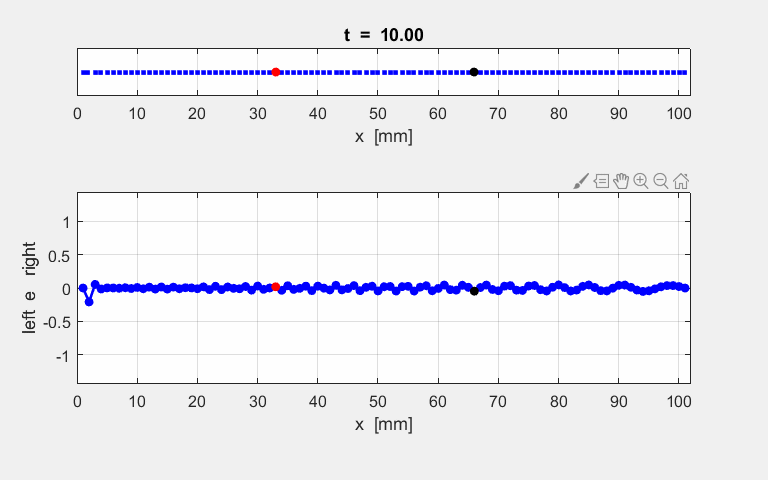
Fig. S1.1.     Table of model parameters displayed in a Figure Window. The peak value of the frequency was estimated from the Fourier Transform of the time evolution of atom #33 and the peak wavelength estimated from the displacement of all the atoms at the end of the simulation time interval.

 

 

The animated motion of the chain of atoms is shown in figure S2. The displacements are shown also as a transverse ones for the sake of clarity in the representation.

 

 

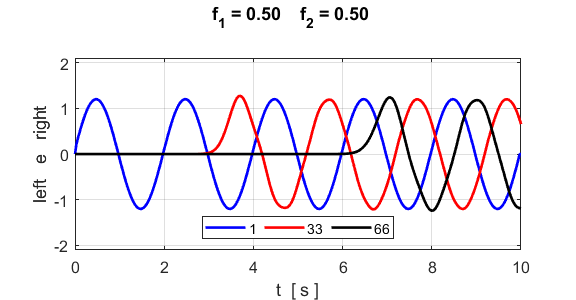
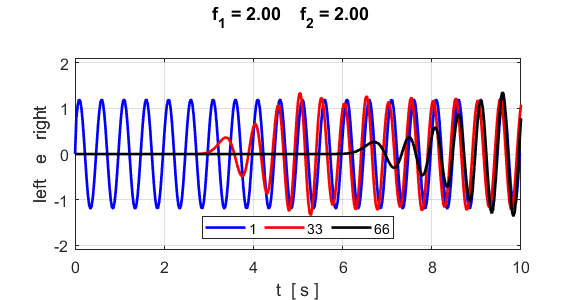
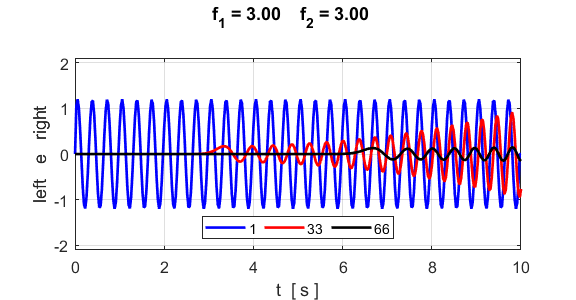
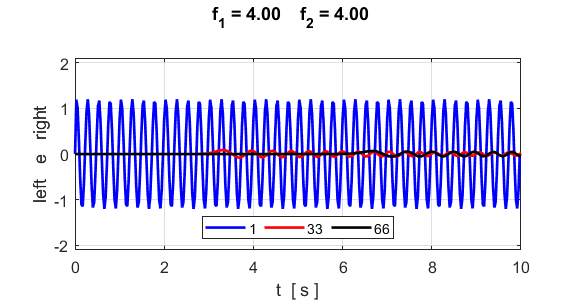
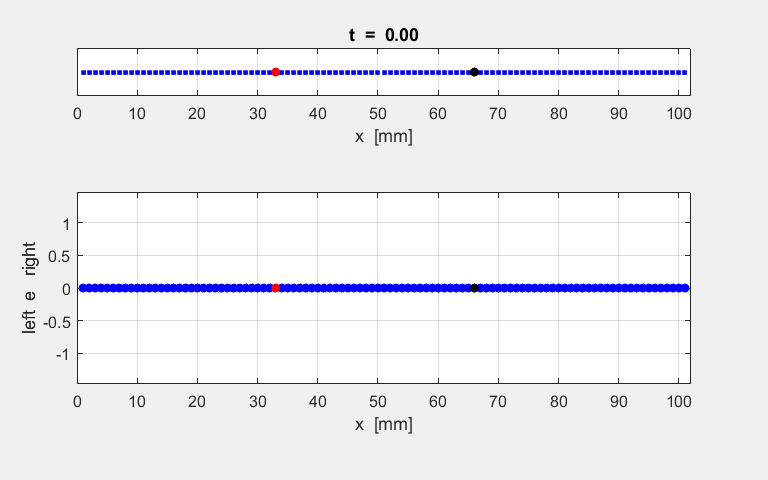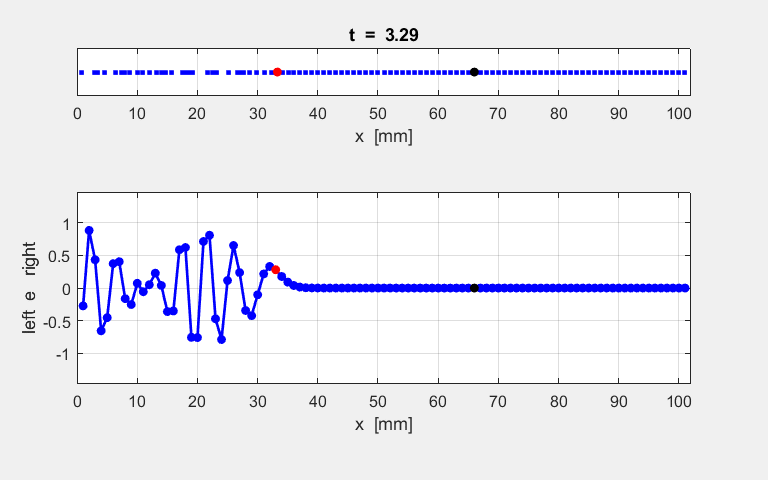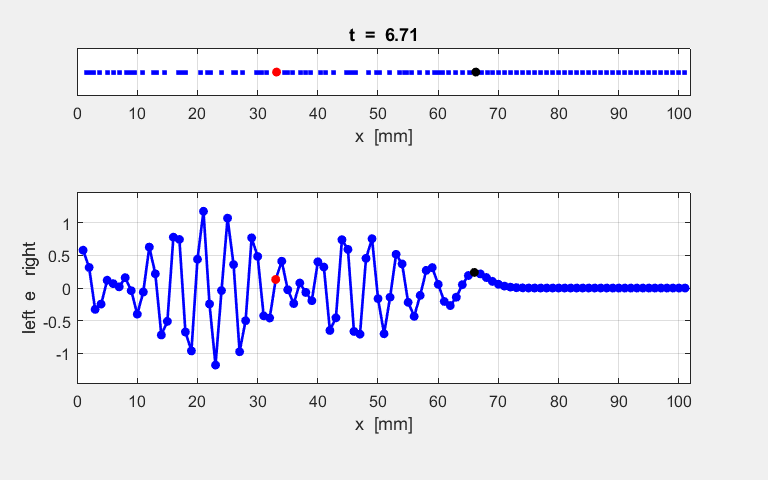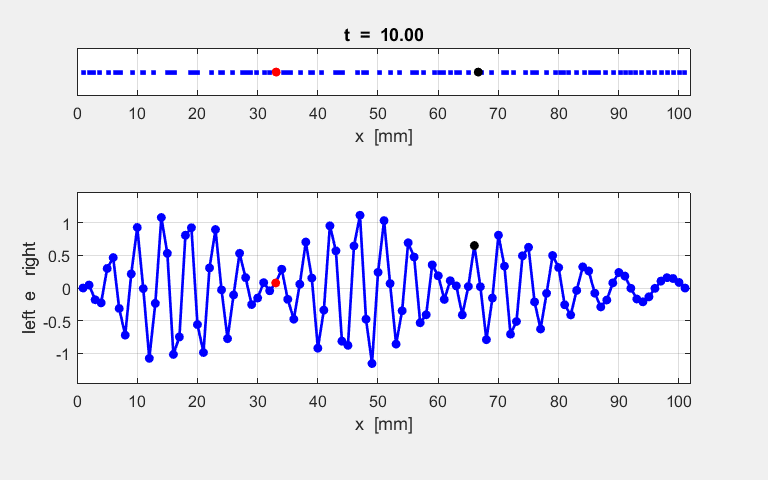
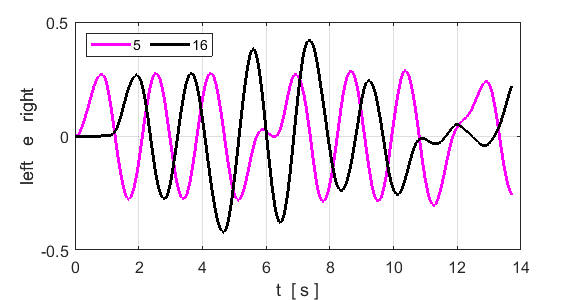
   Fig. S1.2.   Animation of the motion of a sinusoidal wave propagating along the atomic lattice.

 

 

The motion of two atoms (#33 and #66) and the excited atom (#1) as functions of time are displayed in the following plot. The atoms for the plot are specified by the variables n1 and n2.

% INPUT: Atoms for Fourier Transform and plots

   n1 = 33; n2 = 66;

 

The velocity of the peak propagating along the lattice can be estimated from the plot in figure S1.3 and the estimate agrees with the value calculated from the Fourier Transforms as shown figure S1.1.

                

 

 

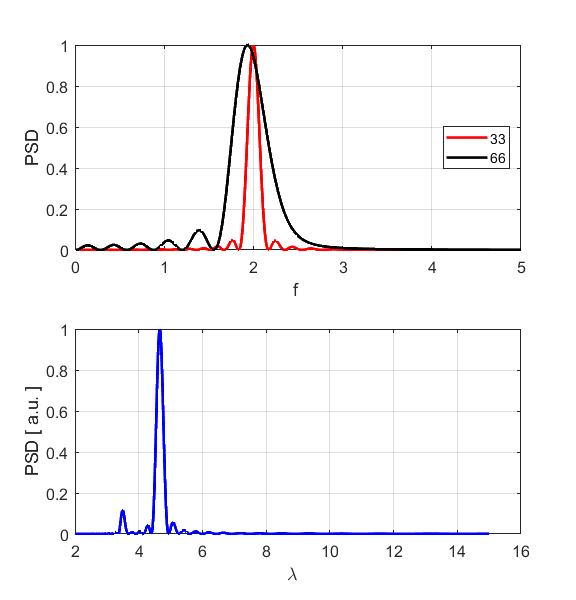
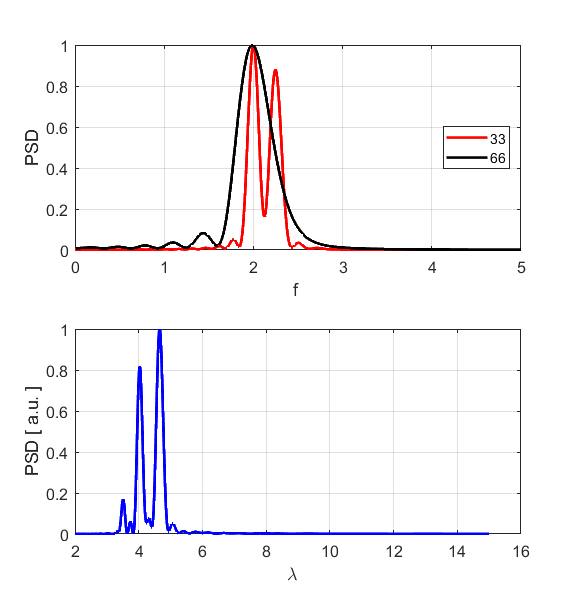
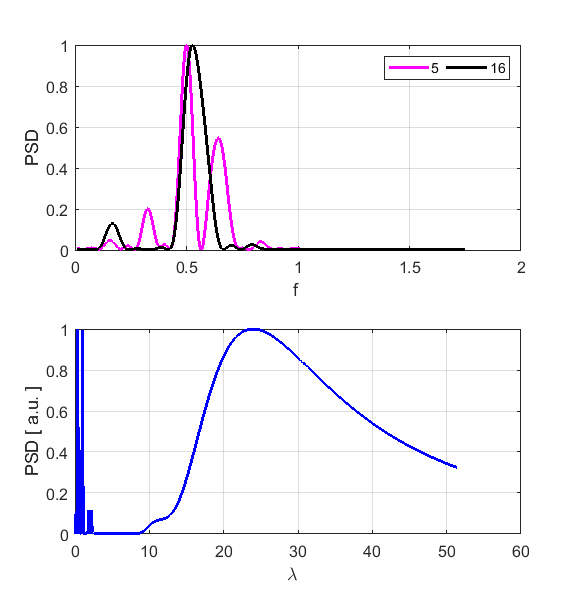
         Fig. S1.3     Time evolution of the motion of atoms #1, #33 and #66.

 

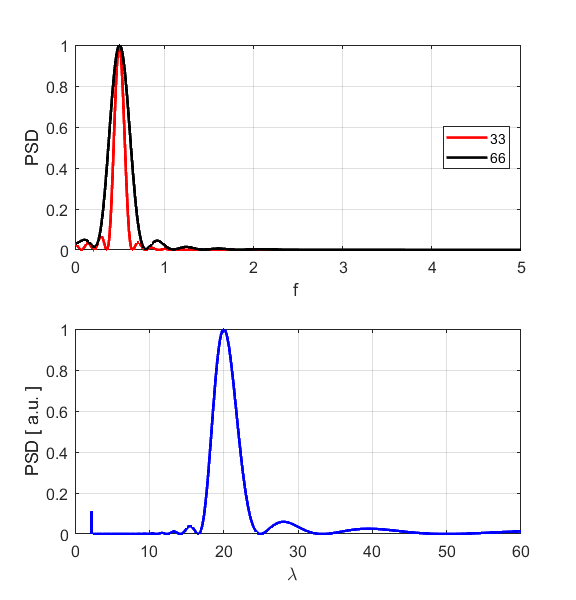
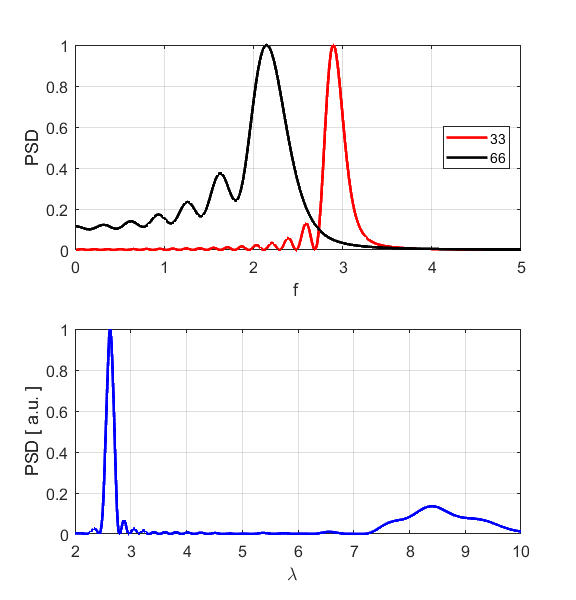
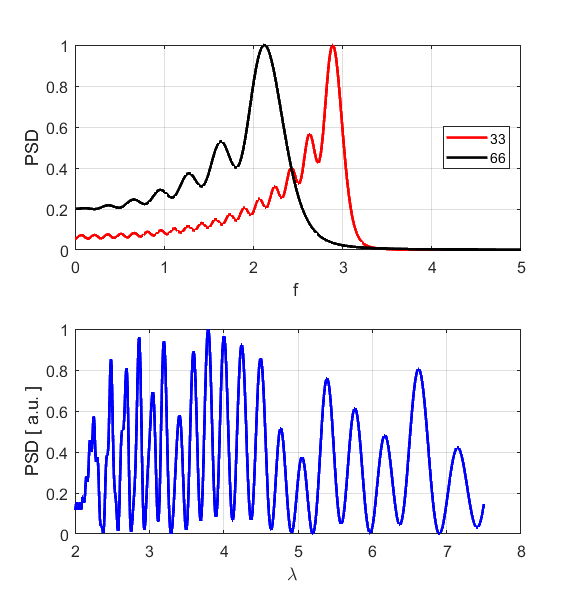
By computing the Fourier Transforms for time/frequency and displacement/wavelength we can estimate the peak values for the frequency and wavelength respectively and hence estimate the phase velocity of the sinusoidal wave (figure S1.4).

      Fig. S1.4.     Fourier Transforms showing very distinct peaks. 

 

The results of the simulation shown that there is a reasonable agreement between the theoretical values for the angular velocity  (equation 6) and the phase velocity  (equation 7) as functions of propagation constant k and their estimates from the plots and Fourier Transforms.

 

 

Simulation #2     Propagation of a monochromatic wave     oscC00ND.m

 

As you increase the excitation frequency, the wavelength of the wave decreases (propagation constant increases) and because of the dispersion effect, the speed of propagation decreases.

 

Fig. S2.1.  At the higher frequency of the excitation, the sinusoidal wave propagates more slowly along the atomic lattice.

 

     Fig. S2.2.

Fig. S2.3.   Eventually, each atom will vibrate at frequency which is close to the driving frequency.

     Fig. S2.4.   Fourier Transforms.  

 

 

Simulation #3     Propagation of a monochromatic wave         oscC00ND.m

 

As the driving frequency approaches the maximum allowed frequency of vibration, the speed of propagation falls dramatically. This is shown in the following simulation when the driving frequency is set to 3.

 

Fig. S3.1.  The propagation speed is considerably less than the maximum phase velocity at this high frequency excitation. Again, there is reasonable agreement between the estimates using the Fourier Transform results and the theoretical predictions.

 

Fig. S3.2. At higher frequency the speed of propagation is less.

 

 

Fig. S3.3.  Since the speed of propagation is slower, it takes longer for the wave to propagate and cause the atoms to vibrate at the excitation frequency.

 

Fig. S3.4.  The Fourier Transforms have multiple peaks since it takes longer time for a more “pure” propagating sinusoidal wave to be generated.



Simulation #4     Non-propagating disturbance      oscC00ND.m

When the driving frequency is set at f1 = 4 which is greater than the maximum allowed frequency (fMax = 3.18), a propagating wave in not generated, and only a small disturbance travels along the atomic lattice. This is because the atoms cannot vibrate with large amplitudes at these high frequencies.

 

Fig. S4.1.     A small disturbance is propagated along the atomic lattice. and not a sinusoidal wave.

 

Fig. S4.2.  As shown in the frequency spectrum, there are no component frequencies with values greater than the maximum allowed frequency. Since no wave propagates, the wavelength spectrum is meaningless.

 

 

 

Simulation #5     Superposition of two sinusoidal wave trains     oscC00ND.m

You can investigate the propagation of a wave which is the superpositions of two sinusoidal signals. As an example, consider two waves with frequencies values of 2.00 and 2.25 and amplitudes of 0.60 propagating along a lattice of 101 atoms (m = 0.10 and kS = 10).

 

Propagation of wave #1: frequency = 2.00     wavelength = 4.66     propagation speed = 9.31

Propagation of wave #2: frequency = 2.25     wavelength = 4.03     propagation speed = 9.06

 

Due to the dispersion, the higher frequency wave propagates more slowly.

 

Fig. S5.1.    The two waves interfere with each other. As the wave propagates, the phase between the two waves continually changes because of the small difference in frequencies and the difference in propagation velocities of the two waves. When the waves are in phase constructive interference occurs and the waves reinforce each other. At other times the two waves interfere destructively and cancel each other. The resulting waveform shows the familiar beat pattern.

 

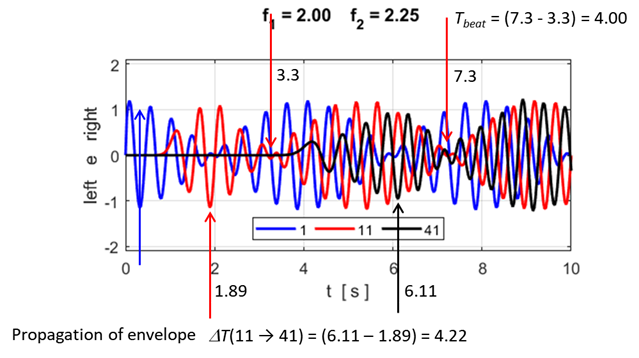
Fig. S5.2.     The two peaks correspond to the two sinusoidal waves exciting the lattice to vibrate. Wave #1:      Wave #2:

 

From the displacement from for atoms #1, #33 and #66 you can estimate the beat period, beat frequency and the group velocity  (speed at which a node or peak advances).

 

Fig. S5.3.   Time evolution of the motion of atoms #1, #11 and #41.

 

From the displacement vs time plot, the beat period and beat frequency are

              

 

which agrees with the theoretical values .

The estimate for the group velocity is from the plot is

            

 

The estimate of the theoretical group velocity (equation 7) is

           

 

Our two estimates are similar. The envelope propagates along the lattice more slowly than either sinusoidal wave.

 

 

NORMAL MODES

 

You can explore the normal modes of vibration that satisfy the boundary conditions that the displacement at the two ends of the lattice chain are zero. A normal mode is characterized by a set of stationary positions for the nodes and antinodes along the chain of atoms. The longitudinal displacements of the atoms are significant only when the when an external driving force has a frequency near one of the natural frequencies of the atomic lattice. This excitation of the system at one of its natural frequencies is called resonance. 

 

The boundary conditions are such that there are nodes at each end of the chain of N atoms. The equilibrium separation distance between the atoms is d. Hence, the length L of the lattice is . Any vibrations of the form

     (11)   

 

where

     (12)                         normal mode number   

 

satisfies the boundary conditions and hence gives a normal mode of vibration of the system.

 

The phase velocity  of the wave propagating along the lattice is

     (4A)    

 

 

In the long wavelength regime, k is small, and the phase velocity is essentially constant and equal in value to its maximum value

     (4B)      

 

The maximum frequency and propagation constant of the wave that can propagate along the lattice is

      (3)      

 

 But, since there are N atoms in a chain of length L, each separated by a distance d and the shortest wavelength  and the highest mode that can be excited is

            

 

However, the mode  must be excluded since all the atoms will not move if the boundary conditions are to be satisfied. The number of modes of vibration under these boundary conditions is then .

 

 

Simulation #7     oscC00NE.m

The Script oscC00NE.m can be used to explore the behaviour of the [1D]  atomic lattice.

The default input values used in the simulation are:

               

Note: if Nt is too small the displacements diverge to infinity.

 

The calculated wave parameters are

            

 

Theoretical predictions:

            Fundamental mode (1st harmonic)  

 

            Harmonic series       

 

In running the simulation, it is best to apply the driving force at the location of an antinode.  The driving force is sinusoidal and specified by its driving frequency fDO, amplitude AD and the atom being driven nE. The Fourier Transform (time/frequency) is calculated for atoms n1 and n2.

 

% >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

% Driving force parameters: Select an atom at an antinode for excitation

% INPUT: [frequency fD0 = 1/6 Hz  /  amplitude frequency AD = 0.08]

%        [Particle to be excited by driving force nE (comment / uncomment)]

%        [n1 n2  atoms for Fourier Transform t/f calculations

  fD0 = 1/6;   

  AD = 0.08;

  nE = ceil(N/2);   % odd harmonics

 % nE = ceil(N/4);    % even harmonics

  n1 = nE; n2 = nE-5;

% >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 

 

The Script is suitable to model only the longwave harmonics where the velocity of propagation is essentially constant at the maximum value.

 

 

Fundamental mode    n = 1      fD0 = 1/6     AD = 0.08     nE = n1 = 16     n2 = 11

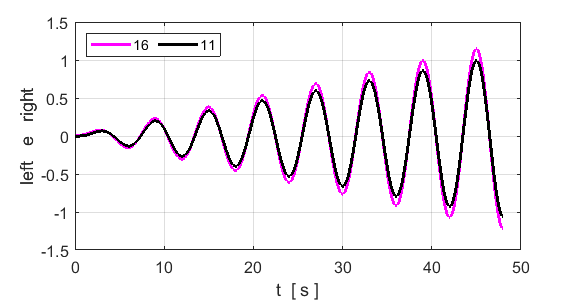
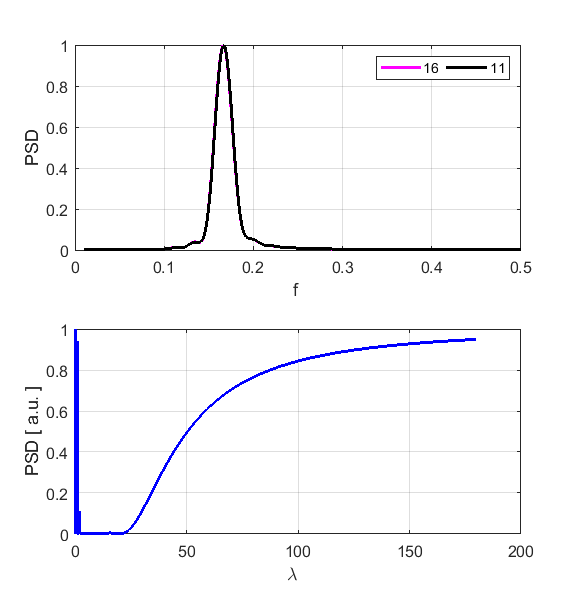
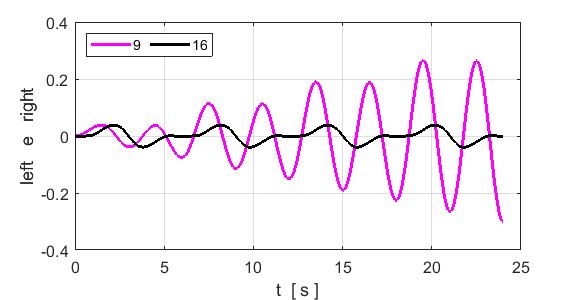
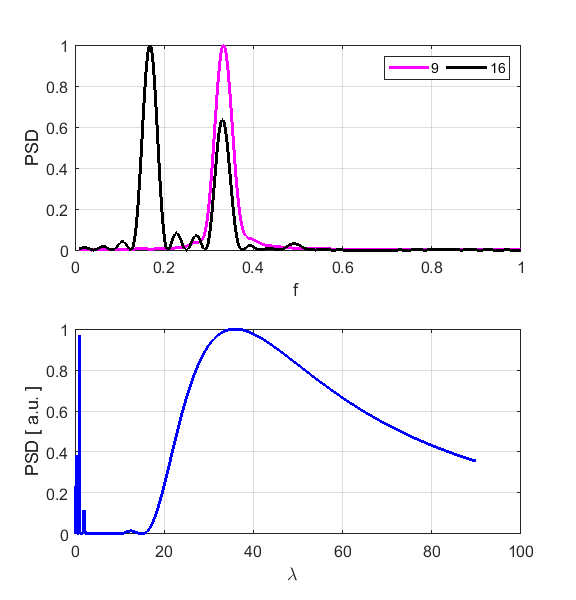
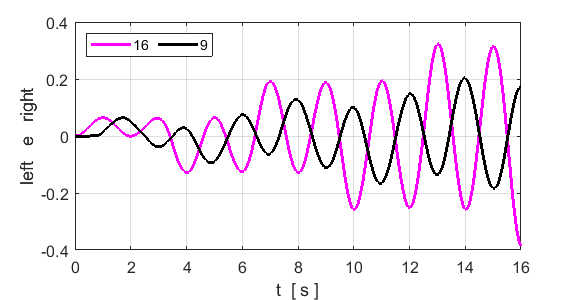
All atoms vibrate in phase with the same frequency and move in the same direction back and forth along the lattice. The peak frequencies are 0.1665 and 0.1666 for atoms 16 and 11 respectively. Theoretical prediction is f1 = 0.1667. The Fourier Transform of displacement could not find the peak wavelength for the fundamental mode.

 

 

2nd harmonic     n = 2      fD0 = 2/6     AD = 0.08     nE = n1 = 9     n2 = 16

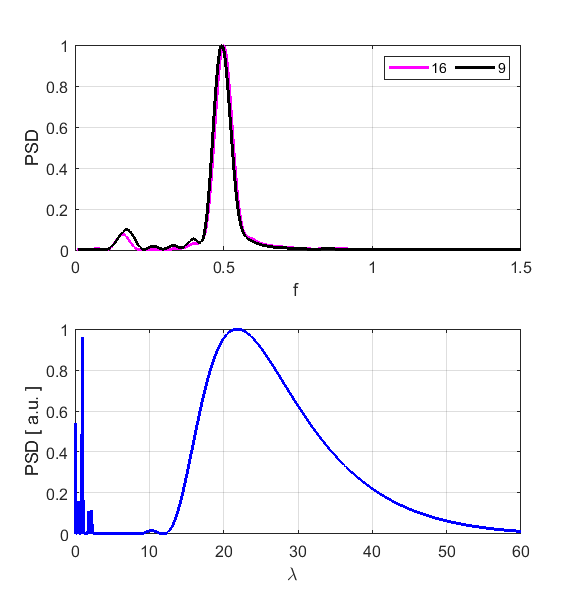
The lattice is excited by the driving force applied to an antinode at the site of atom 9. The 2nd harmonic is excited by the driving force. The motion of atom 16 corresponds to a node. It is not a “true” node as this atom vibrates with a small amplitude. The peak frequencies are 0.3329 and 0.3306 for atoms 9 and 16 respectively. Theoretical prediction is f2 = 0.3333. The Fourier Transform of displacement gives a peak wavelength of 35.8 (theoretical value ).

 

 

3rd harmonic     n = 3      fD0 = 3/6     AD = 0.20     nE = n1 = 16     n2 = 9

Note: for higher harmonics, it may be necessary to increase the amplitude AD of the driving force.

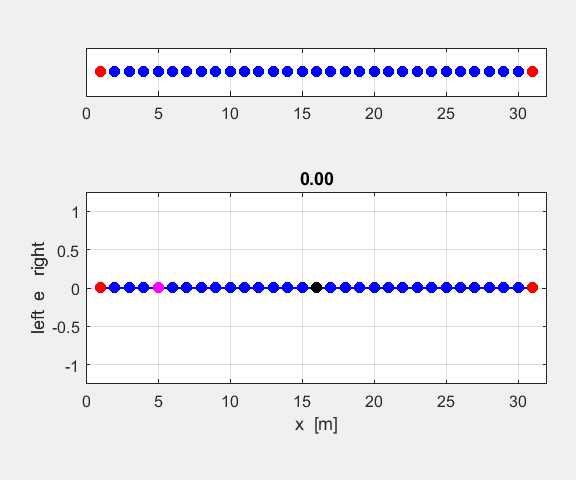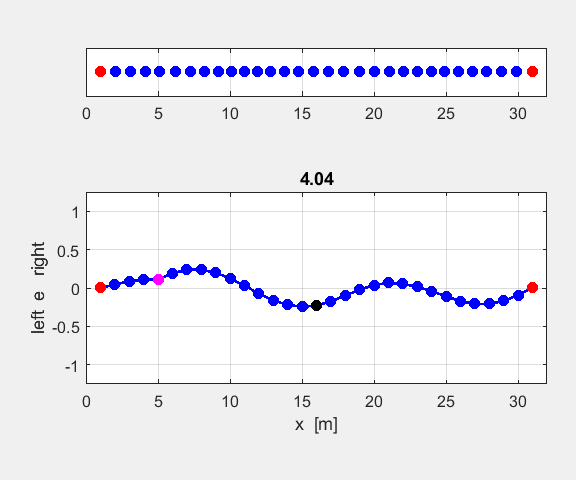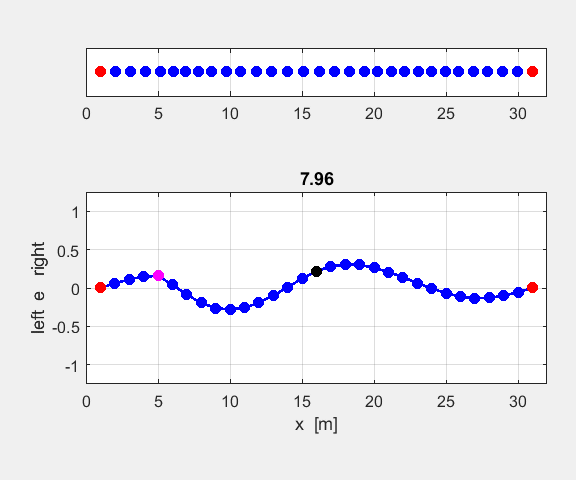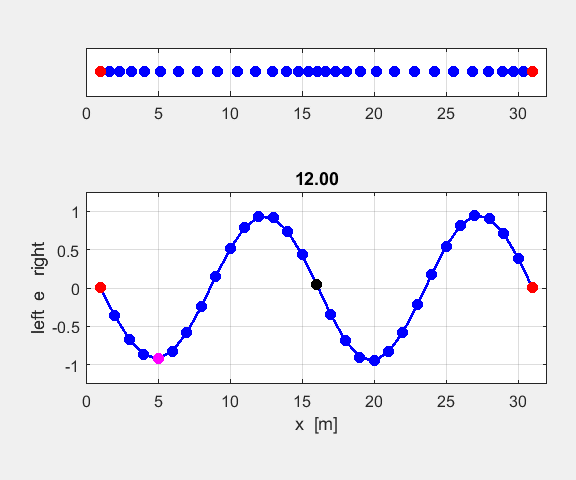
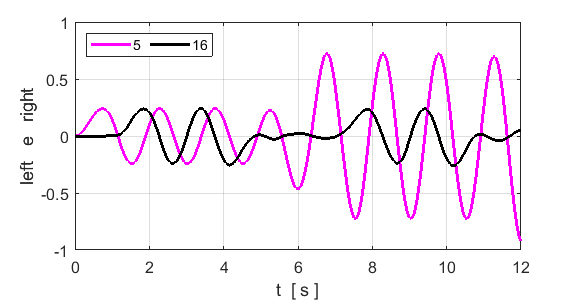
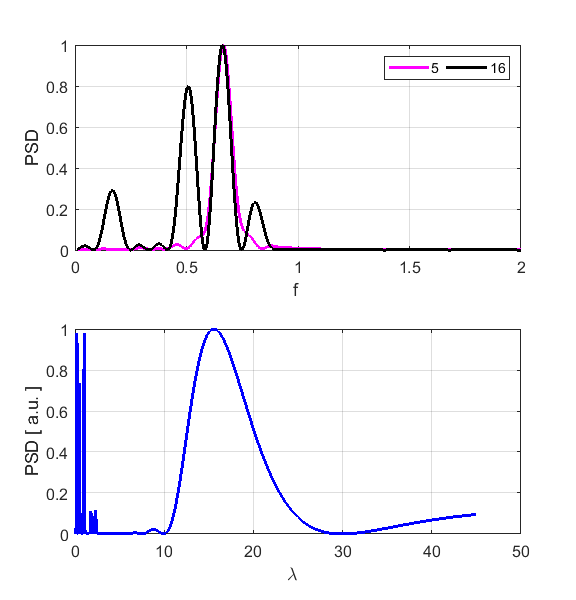
The lattice is excited by the driving force applied to an antinode at the site of atom 16. The 3rd harmonic is excited by the driving force. The motion of atom 16 corresponds to a antinode which vibrates at the frequency 0.4991 (theoretical prediction is f3 = 0.5000. The Fourier Transform of displacement gives a peak wavelength of 21.8 (theoretical value ).

 

 

4th harmonic     n = 4      fD0 = 4/6     AD = 1.00     nE = n1 = 5     n2 = 16

 

The lattice is excited by the driving force applied to an antinode at the site of atom 5. The 4th harmonic is excited by the driving force. The motion of atom 16 corresponds to a node. It is not a “true” node as this atom vibrates with a small amplitude. The peak frequency at the antinode site of atom 5 is 0.6653 (theoretical prediction is f4 = 0.6667. The Fourier Transform of displacement gives a peak wavelength of 15.6 (theoretical value ).

 

 

Non-resonance excitation           fD0 = 3.5/6     AD = 1.00     nE = n1 = 5     n2 = 16

The system is not driven at one of its natural frequencies of vibration. You get a much more complicated motion with smaller displacements of the atoms.

System driven at a frequency which is not equal to one of the natural frequencies of vibration. This results in a more complicated motion of the atoms and the displacements are smaller than if driven at a natural frequency.