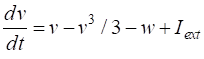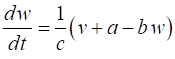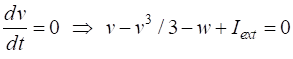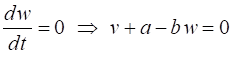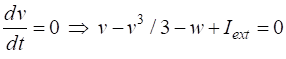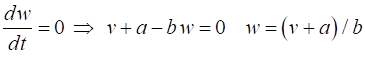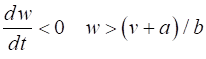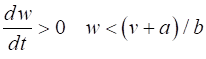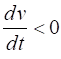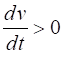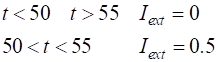|
FITZHUGH-NAGUMO MODEL FOR SPIKING NEURONS Ian Cooper Any comments,
suggestions or corrections, please email me at
matlabvisualphysics@gmail.com |
|
MATLAB cnsFNA.m The technique of phase plane analysis is used to model the action potentials generated by neurons with the Fitzhugh-Nagumo Model. The dynamics of the two- state variable system (membrane potential v and recovery variable w) can be explored. The function ode45 function is used to solve the pair of coupled differential equations. The variable y gives v and w. Most of the parameters are specified in the INPUT SECTION. For different models it may be necessary to make some changes to the Script. The results are displayed in as a phase space plot and a time evolution plot. By changing the parameters within the Script, you can investigate in detail the dynamics of the Fitzhugh-Nagumo model of a spiking neuron and explore all the essential aspects of the model. The coupled pair of differential equation is solved using the ode45 function % K use to pass variables to
function FNode K = [Iext;
a; b; c]; % Solve differential equations
using ode45
[t,y] = ode45(@(t,y)
FNode(t,y,K), tSpanT,y0); function dydt = FNode(t,y,K) a = K(2); b = K(3); c = K(4); Iext = K(1); %Iext = 0.003 * t; %if t
> 50; Iext = 0.5; end %if t
> 55; Iext = 0; end dydt =
[(y(1)-y(1)^3/3-y(2)+Iext); (1/c)*(y(1) + a -
b*y(2))]; end |
|
ACTION POTENTIALS Nerve cells are separated from the extracellular region by a lipid bilayer membrane. When the cells aren’t conducting a signal, there is a potential difference of about -70 mV across the membrane (outside of the membrane the potential is taken as zero). This potential difference is known as the cell’s resting potential. On both sides of the nerve cell membrane, the concentrations of positive ions such as sodium, potassium and calcium and negatively chlorine ions and protein ions maintain the resting potential. When the cell receives an external stimulus, an action potential maybe evoked where the membrane potential spikes toward a positive value, in a process called depolarization, after which, repolarization occurs where the membrane potential resets back to the resting potential. In one example, the concentration of the sodium ions at
rest is much higher in the extracellular region than it is within the cell. The
membrane contains gated channels that selectively allow the passage of ions
though them. When the cell is stimulated, the sodium channels open and there
is a rush of sodium ions into the cell. This sodium “current”
raises the potential of the cell, resulting in depolarization. However, since
the channel gates are voltage driven, the sodium gates close after a while.
The potassium channels then open and an outbound potassium
current flows, leading to the repolarization of the cell. In 1952, Hodgkin and Huxley explained this mechanism of
generating action potential through their mathematical model. While this was
a great success in the mathematical modeling of biological phenomena, the
Hodgkin-Huxley model is complicated. However, in 1961, R. Fitzhugh and J. Nagumo proposed a mathematical neuroscience model
referred to as FitzHugh-Nagumo model. This model is a simpler
version of the Hodgkin-Huxley model which demonstrates the spiking potentials
in neurons and emulates the potential signals observed in a living
organism’s excitable nerve cells. The Fitzhugh-Nagumo model has only
a few parameters and two coupled differential equations for the membrane potential, v, and the recovery variable w, which modulates v. FITZHUGH-NAGUMO MODEL The pair of coupled first order equations defining the Fitzhugh-Nagumo Model are (1A)
(1B) The
variable v
is a voltage-like membrane potential
having cubic
nonlinearity that allows regenerative self-excitation via a positive feedback
and w is
called the recovery
variable having linear dynamics that provides a slower negative feedback. The
parameter The two nullclines in the v-w plane are given by
v-nullcline
w-nullcline The intersection of the two nullclines gives the critical points (fixed equilibrium points) of the model. The slope of the straight-line
The parameter
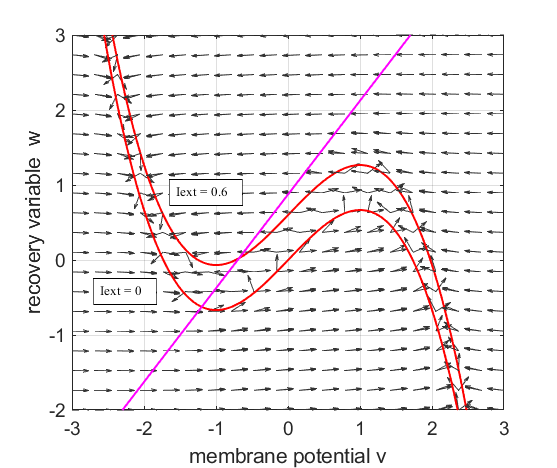
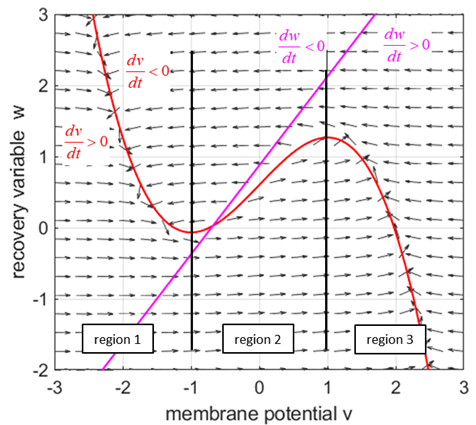
Fig. 1.
The red curves are the v-nullcline and the magenta straight line is the w-nullcline. The intersection of the v-nullcline and the w-nullcline gives the single critical point of the system. An increase in the
external current stimulus cnsFNA.m
The statement close all is commented out and a break point inserted before the
trajectory is plotted. Then the Script is run for different values of We can estimate the coordinates of the critical point in
v-w phase space by solving the equations numerically using
the Matlab function vpasolve and then output the results in the Command Window. (2A) (2B) % Critical point - output to
Command Window syms p Sp = vpasolve(p-p^3/3-(p+0.7)/0.8 + Iext
== 0,p,[-3 3]); Sq = (Sp+a)/b; disp('Critical
point'); fprintf(' v_C
= %2.2f\n', Sp); disp(' ') fprintf(' w_C
= %2.2f\n', Sq); DYNAMICS OF THE FITZHUGH-NAGUMO MODEL To the left of the straight-line w-nullcline, the rate of change of w is negative and to the right it is positive; left For the v-nullcline, above the line the rate of
change of v
is negative, while below the line is positive
above
Fig. 2.
Critical point is in region 2. The vector field (direction of the
arrows) indicates the sign of Small external stimulus
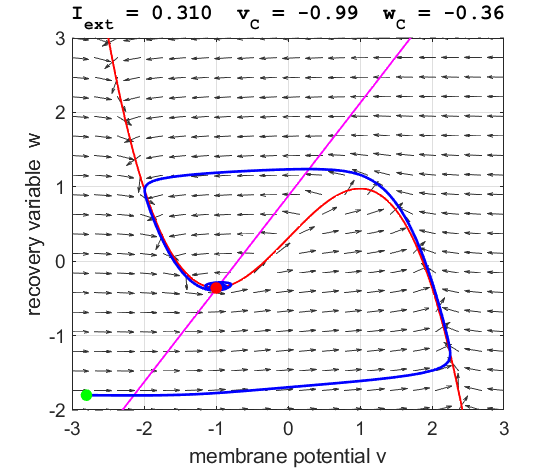
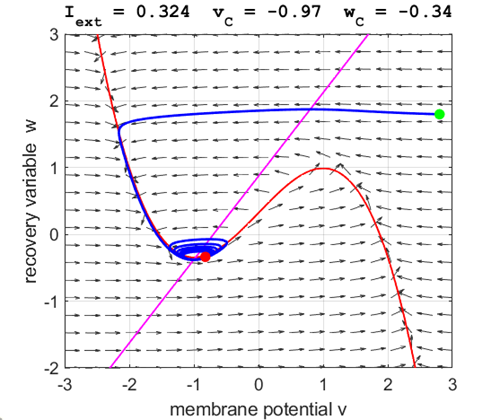
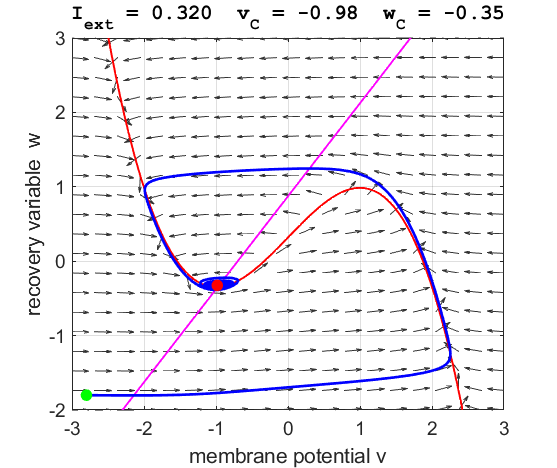
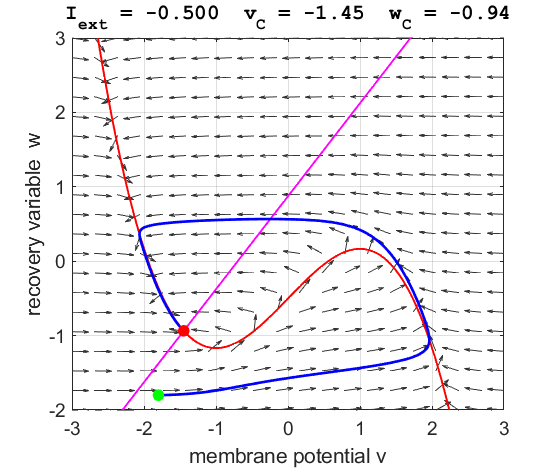
currents The critical point is in region 1. The state variables evolve to
the critical point without exciting a spike in the potential v (figure
3).
Fig. 3A. The
phase space trajectory is attracted to the critical point. The green dot gives the starts and the red dot gives
the end of the trajectory.
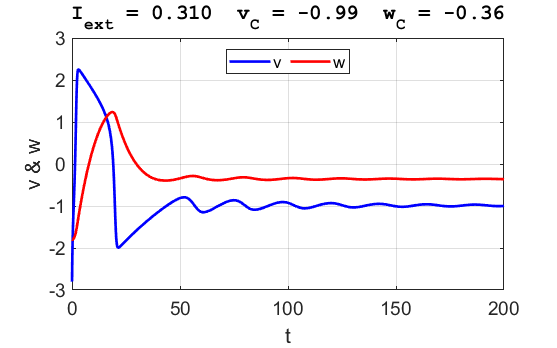
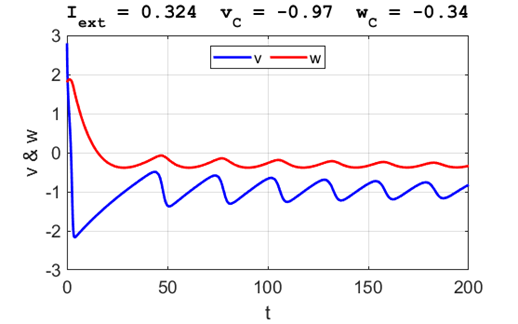
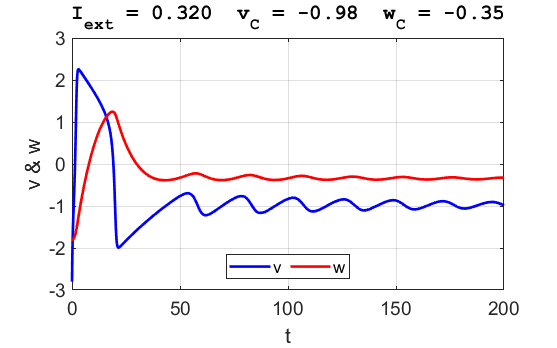
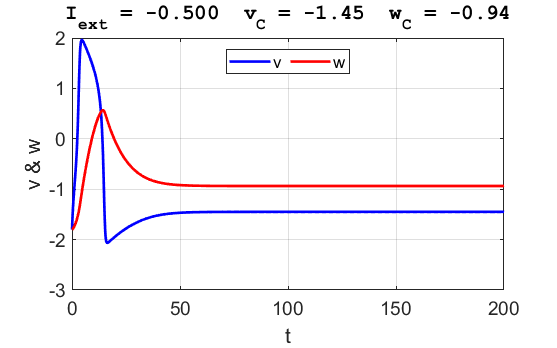
Fig. 3B. The time evolution of the two state variables.
There are small oscillations which become quickly damped around critical
point.
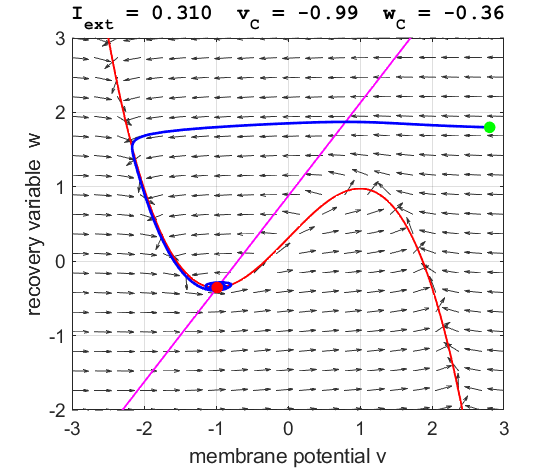
Fig. 3C. The
phase space trajectory is attracted to the critical point. The green dot gives the starts and the red dot gives
the end of the trajectory.
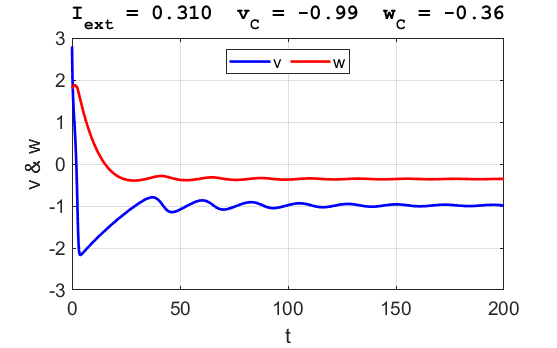
Fig. 3B. The time evolution of the two state variables.
There are small oscillations which become quickly damped around critical
point. For an external current stimulus, For weak current stimuli, there is a stable fixed equilibrium point.
Fig. 4.
The critical point is at the boundary of regions 1 and 2. The
trajectory oscillates around the critical point without an action potential
being produced. Intermediate external stimulus
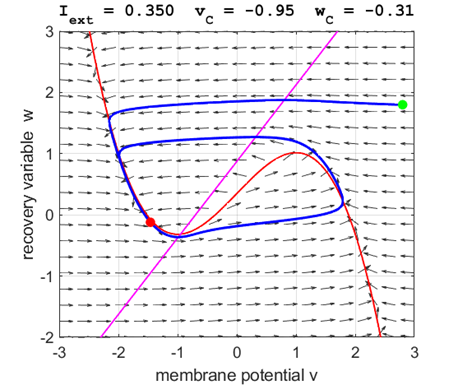
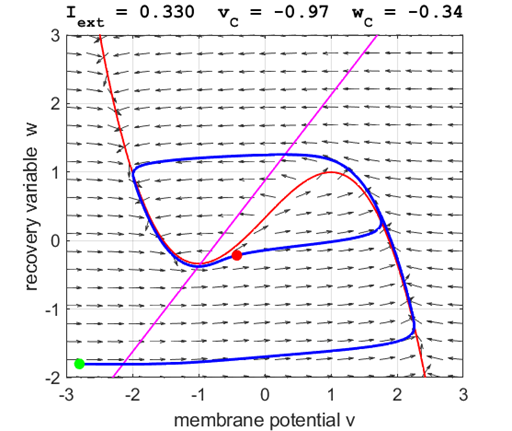
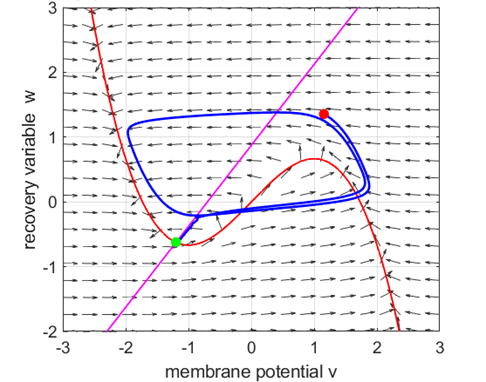
currents The critical point is in region 2 and is an unstable
equilibrium point. A series of action potentials are generated. The neuron
spikes repetitively, that is, the model exhibits periodic (tonic spiking) activity.
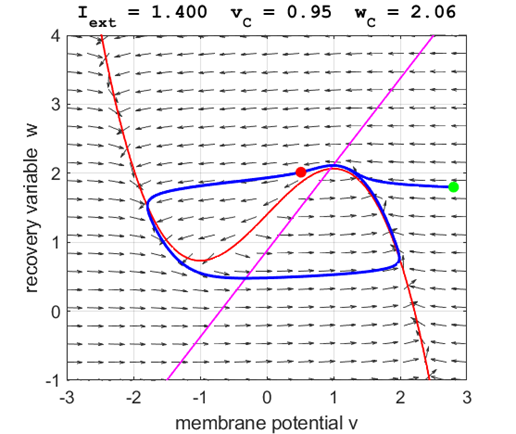
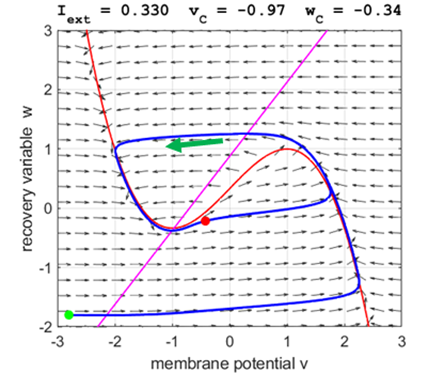
Fig. 5A.
The critical point acts as a center and is in region 2. The trajectory
forms closed loops around the critical point which results in the repetitive
spiking of the neuron. At the start, v decreases and w remains nearly unchanged. When the trajectory approaches
the v-nullcline,
Fig. 5B.
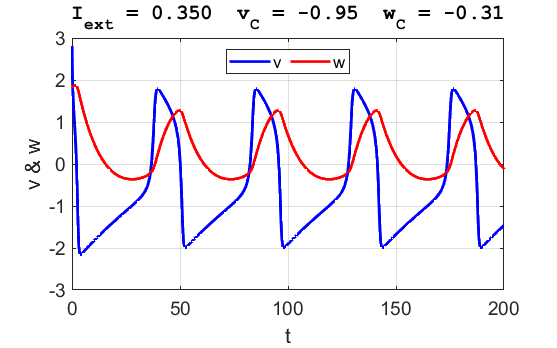
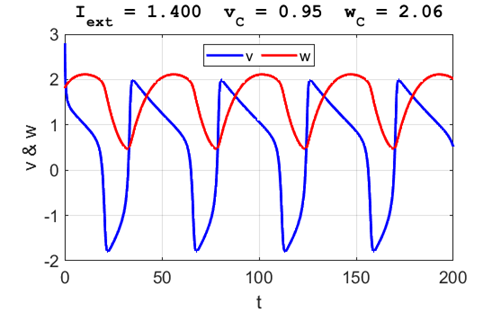
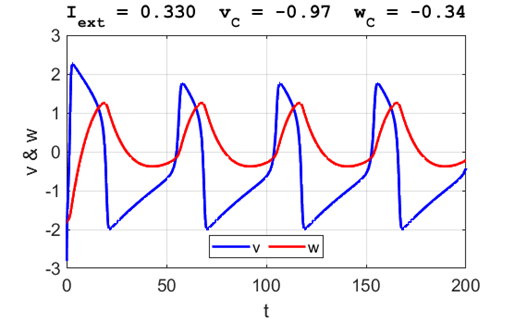
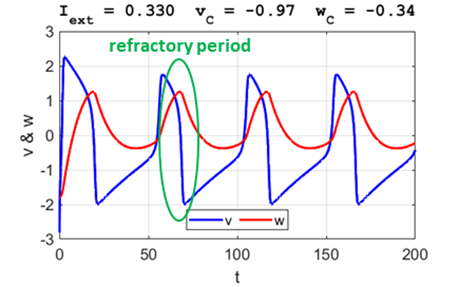
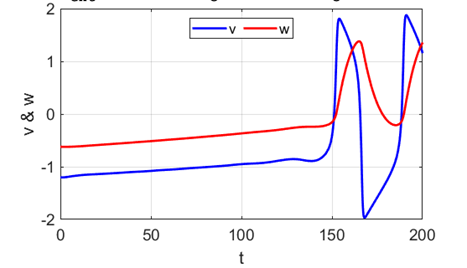
A series of action potentials are produced. The fixed equilibrium
point is unstable and leads to tonic firing of
the neuron.
Fig. 5C.
The critical point acts as a center. The trajectory forms closed loops
around the critical point which results in the repetitive spiking of the
neuron. It is possible to get a single
spike generated by carefully adjusting the value
Fig. 5D. A single spike is produced when We can
demonstrate the concept of the Hopf bifurcation.
A Hopf bifurcation occurs when there is a
qualitative change in the system dynamics as the system parameters are
varied. When
Fig.
5E. The phase space
trajectory is attracted to the critical point.
Fig. 5F. The phase space
trajectory is attracted to the limit cycle and the neuron spikes
periodically. After a spike, the neuron returns to its resting state during the refractory
period where the system is indifferent
to any external stimuli (figure 5G).
refractory
period
Fig. 5G. The phase space
trajectory is attracted to the limit cycle and the neuron spikes
periodically. After a spike, the neuron returns to its resting state during
the refractory
period where the system is
indifferent to any external stimuli. Large external stimulus
currents
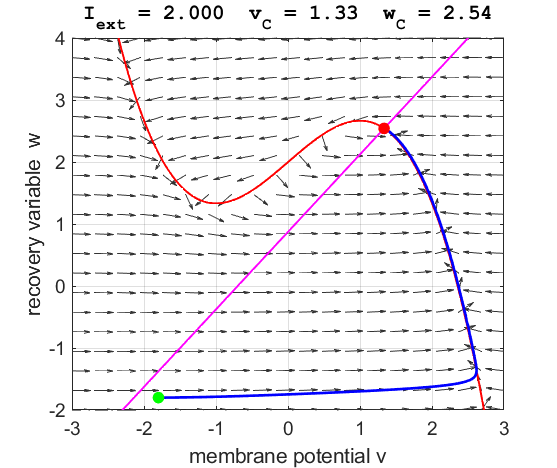
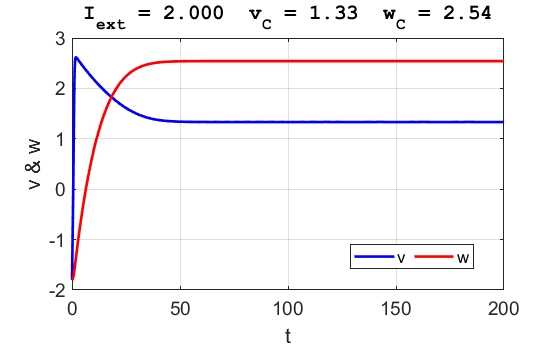
Fig. 6.
The critical point is in region 3. The trajectory is attracted to the
critical point. No action potentials are generated. At the start SUMMARY
The, Fitzhugh-Nagumo model
does not have a well-defined firing threshold, like the Hodgkin-Huxley model.
This feature is the consequence of the absence of all-or-none responses, and
it is related, from the mathematical point of view, to the absence of a saddle equilibrium. The FitzHugh-Nagumo model
explains the excitation block phenomenon, i.e., the cessation of repetitive spiking as the
amplitude of the stimulus current increases. When The Fitzhugh-Nagumo model
explains the phenomenon of post-inhibitory (rebound) spikes, called anodal break excitation. As the stimulus
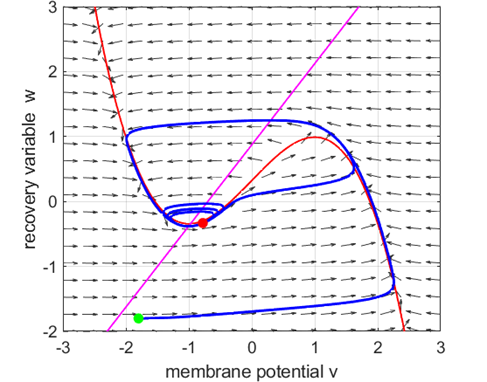
Fig. 7.
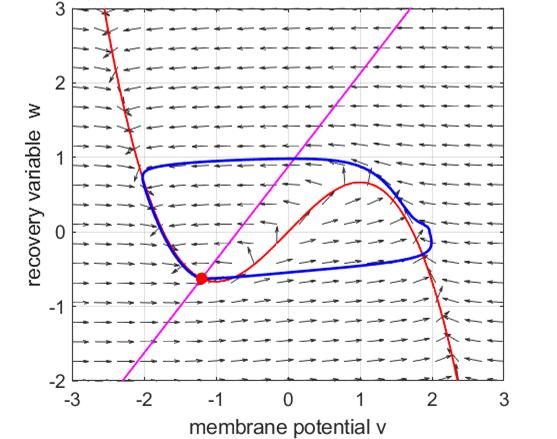
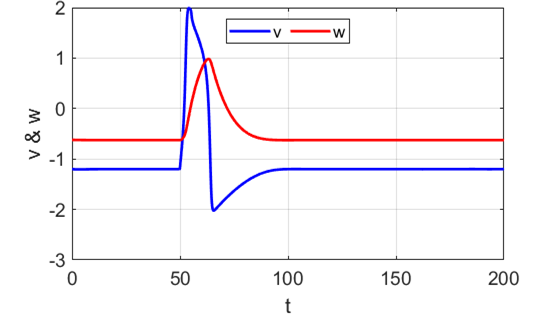
Anodal break excitation (post-inhibitory rebound spike) in the
Fitzhugh-Nagumo model. The FitzHugh-Nagumo model
explained the dynamical mechanism of spike accommodation in Hodgkin-Huxley
model. When stimulation strength
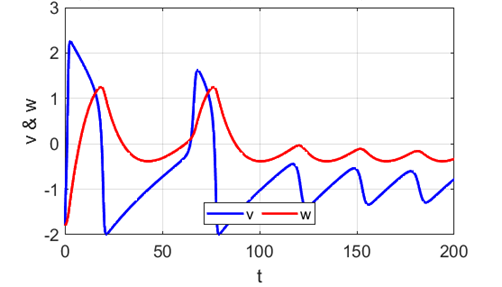
Fig. 8.
Spike accommodation to slowly increasing stimulus in the Fitzhugh-Nagumo model. The external current stimulus used was In contrast, when the stimulation is increased abruptly,
even by a smaller amount, the trajectory cannot go directly to the new resting
state but fires a transient spike (figure 9).
Fig. 9.
Spike accommodation: response to a short current stimulus. The current pulse results in the
firing of a transient spike, like the post-inhibitory (rebound) response. The
neuron is initially in a resting state.
Figures 8 and 9 were produced by making changes to the
function used in the ode45 call. Changes to function dydt = FNode(t,y,K) a = K(2); b = K(3); c = K(4); Iext = K(1); %Iext = 0.003 * t; if t >
50; Iext = 0.5; end if t >
55; Iext = 0; end dydt =
[(y(1)-y(1)^3/3-y(2)+Iext);(1/c)*(y(1)+a-b*y(2))]; end |
|
|