|
Ian Cooper matlabvisualphysics@gmail.com DYNAMICAL
NON-LINEAR SYSTEMS LOGISTIC
DIFFERENCE EQUATION
DOWNLOAD DIRECTORIES FOR PYTHON
CODE pyChaos001.py The logistic difference equation
pyChaos002.py The logistic difference equation Plots: pyChaos0003.py Mapping function F for period 4 dynamics Plot: F vs x F = x, |dF/dx| and equilibrium points Warning: code not perfect in finding the equilibrium points where F = x. Need to change the number of grid points and the tolerance. INTRODUCTION Biologists studying the variability in populations of various species where generations do not overlap found a simple difference equation that predicted the population trajectories reasonably well. One such equation is a simple quadratic equation called the logistic difference equation. Very surprising, this simple difference equation predicts under certain circumstances a fantastically complex and chaotic behaviour that was total unexpected. The logistic difference equation is given by (1) where x(n) is a scaled population at iteration n and
r is the control or growth parameter. The initial condition is
specified by This
simple non-linear system does not possess simple dynamical properties It
is often observed in nature that a population x
will increase from one generation to the next when small and decrease when
large. This is expressed mathematically by the product
Fig.
1. Parabolic plot for the logistics
equation pychaos002.py The population The dynamics of the logistic difference equation is best displayed by observing an animation of the population x(n) as the growth factor r is incremented. For small values of r, the population converges to a stable equilibrium population. However, as the value of r increases, interesting things happen as shown in figures 2 and 3.
Fig. 2. Population x(n) as the growth
factor is incremented from 0 to 1. As r passes through a critical value, complete changes in the dynamics
of the system occur. pyChaos001.py
Fig. 3. Population x(n) as the
growth factor is incremented from 0.6 to 1.
pyChaos001.py When r > ~0.75, This complicated dynamical behaviour is show in a bifurcation diagram and a plot of the Lyapunov exponent (figure 4).
Fig. 4. Bifurcation
diagram - plot of the iterated
values of A useful analytical metric that can help characterize chaos is called the Lyapunov exponent, which measures how quickly an infinitesimally small distance between two initially close states grows over time. This is expressed by the equation where the LHS is the distance between
two initially close states after t steps, and the RHS
is the assumption that the distance grows exponentially over time. λ is the Lyapunov exponent which is
measured for a long period of time (ideally
Thus, the Lyapunov exponent is a time average of
PERIOD 1
DYNAMICS The orbit of the population x is attracted to an equilibrium
point or fixed point Since
Fig.
5. If We
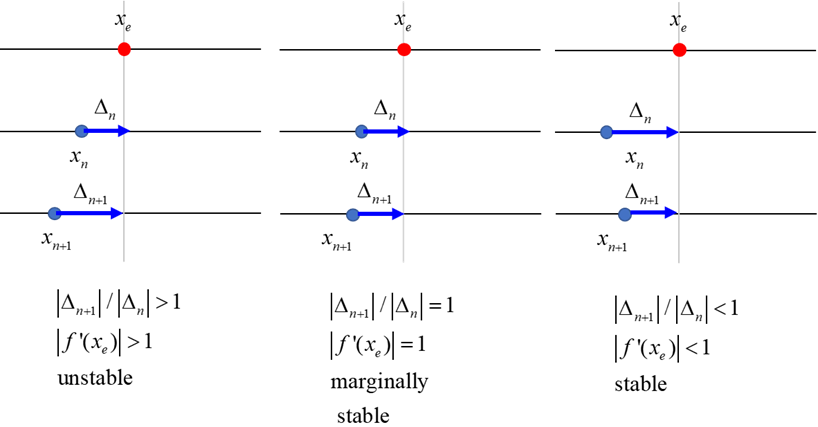
can derive analytical expressions for the fixed points of the [1D] map To determine the stability of the fixed points and we have If If Thus, the local stability criteria for a fixed point
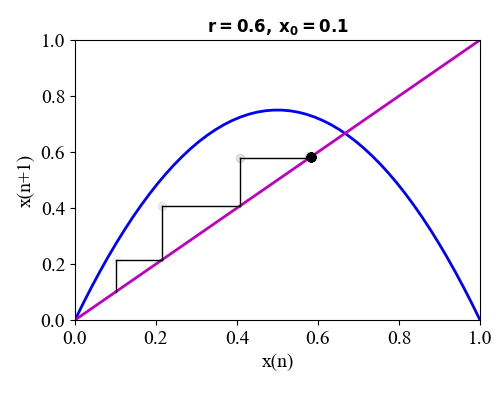
Fig. 6. Stability of fixed points. The first derivative for the non-zero equilibrium point Thus, for the equilibrium point Therefore, we can conclude The local curvature of the curve This dynamic is said to be period 1: Figure 7 shows plot for the case when r = 0.6. This is a stable fixed point since
Fig. 7. Plots of the iterated population PERIOD DOUBLING
DYNAMICS The
bifurcation diagram shown in figure 8 shows an expanded version of the figure
1 plot. It clearly shown the change in the dynamics in the evolution of the
population when
Fig. 8. Bifurcation
diagram - plot of the iterated
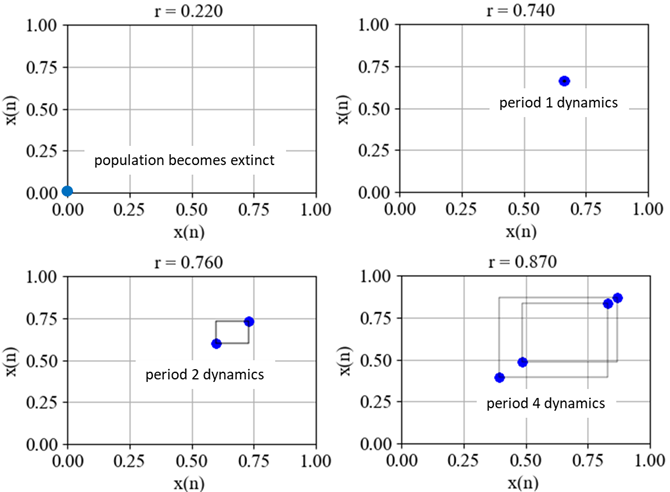
values of When and there are now two attractors of f(x) with fixed points
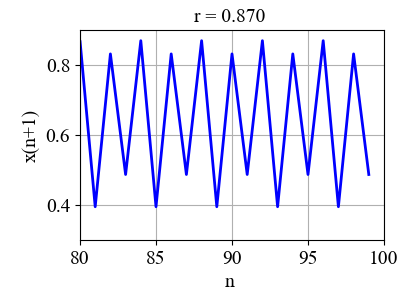
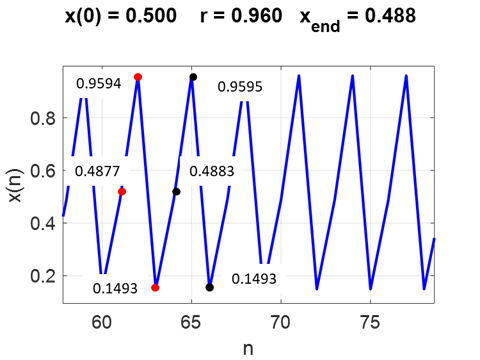
Fig. 9. Period 2 dynamics What happens when the value of r is slightly increased slightly above 3/4? We know from our observations the single fixed point becomes unstable and gives birth (bifurcates) to a cycle of period 2. The population x returns to the same value only after every second iteration the range The period 2 dynamics is only exhibited in the range
Fig. 10. Period 4 dynamics Figure 11 shows
another way in which to analyse the population dynamics for r = 4. The mapping function f4(x) (blue curve); the gradient of the mapping df4/dx (magenta curve); f4
= x (red curve) are plotted against the population x.
The dots show
the equilibrium populations xe where the blue and red curves intersect, xe |df/dx| 0.000 1.000 unstable 0.394 0.343 stable 0.433 1.000 unstable 0.486 0.433 stable 0.832 0.389 stable 0.856 1.000 unstable 0.870 0.258 stable
Fig. 11. Period 4 dynamics Increasing r again will lead to further bifurcations. This phenomenon is called period-doubling period 1 à period 2 à period 4 à period 8 à period 16 à . . .
Fig. 11. Period 8 dynamics Increasing r again
Fig. 12. Population orbits in the chaotic regime
Fig. 13. Bifurcation diagram. Plot of iterated values of x(n) as a function of the growth rate r.
Fig. 14. Period 1 orbit in a narrow window within the region of chaos.
Figure 15 shows another animated view of the changing population dynamics for increasing values of the growth parameter r.
Fig. 15. The population orbit for increasing values of the growth parameter r. pyChoas001.py
Period doubling
window In the period doubling
window, periodic motion again occurs where odd period dynamics may occur as
shown in figures 16 and 17.
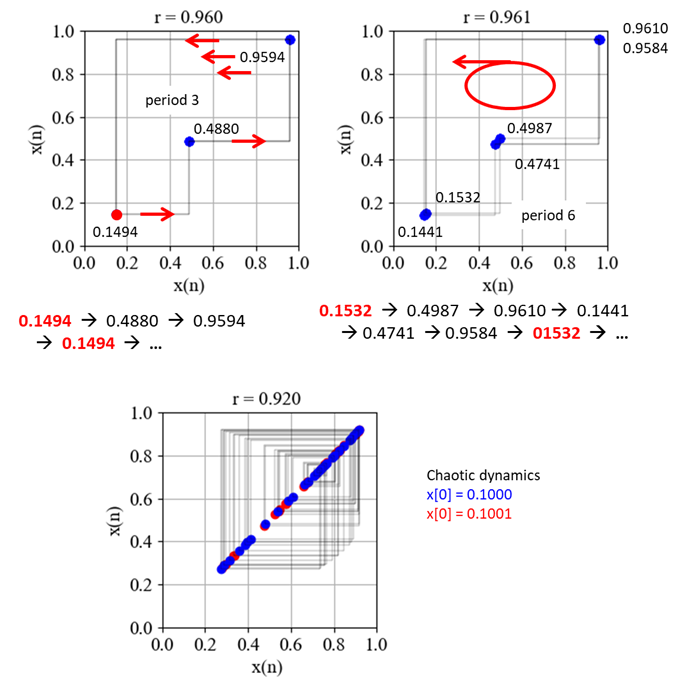
Fig. 16. Period 3 dynamics
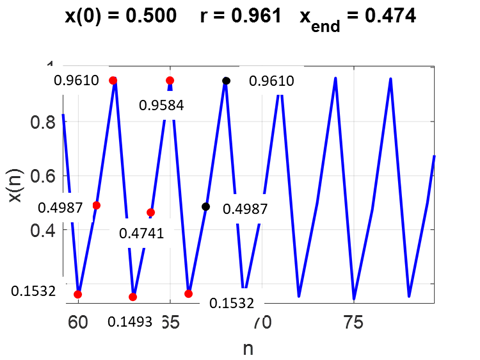
Fig. 17. Period 6 dynamics produced by the
bifurcation of the period 3 dynamics PERIOD DOUBLING –
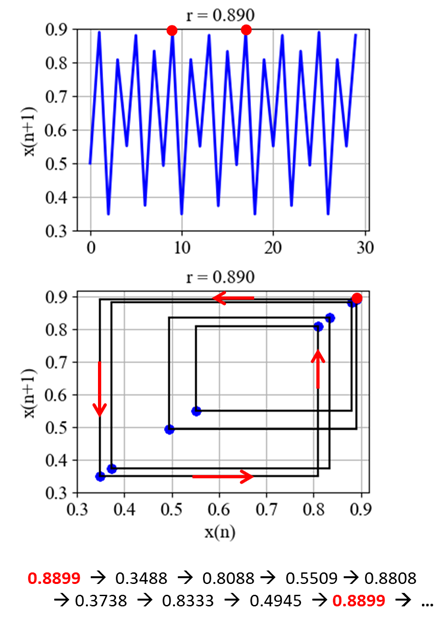
FINDING THE FIXED POINTS OF THE DYNAMICS We can show the dynamics of the logistic difference equation another way by plotting the points (x(n), x(n)) for increasing values of n after any initial transience no longer influences the dynamics. Figure 18 shows the lot with r = 0.890 for period 8 dynamics and who the population cycles through 8 fixed-points.
Fig. 18. 8 period
dynamics. pyChaos002.py chaos23.pptx
Fig. 19. Period doubling and chaotic dynamics. pyChaos002.py chaos23.pptx The logistic difference equation is an exceptionally simple model
of the population growth for
butterflies who lay eggs their eggs in year n and their offspring are born in year
References H. Gould & J. Tobochnik An Introduction to Computer Simulation Methods (Part 1) R. M. May Simple Mathematical Models with Very Complicated Dynamics, Nature 261, 459 (1979) |