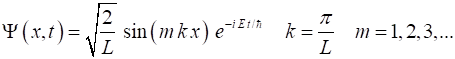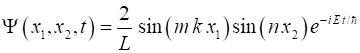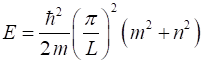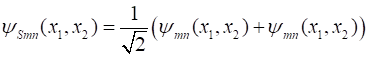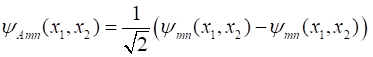DOING PHYSICS WITH MATLAB

 

TWO PARTICLES IN AN INFINITE POTENTIAL WELL

Symmetric and Antisymmetric States

Bosons and Fermions

 

Ian Cooper

Any comments, suggestions or corrections, please email me at

matlabvisualphysics@gmail.com

 

 

MATLAB

DOWNLOAD DIRECTORY FOR SCRIPTS

 

qmTwo.m

Calculation of the probability density function of finding two particles confined within an infinite potential well. Within the Script you can change the quantum numbers m and n. The Script can be modified to a Live Editor Script to better observe the changes in the probability density as the values of m and n are changed.

 

 

Consider two particles confined in an infinite potential well (particle in a box)

 (1)        

 

Assume that the particles do not interact with each other. Then by analogy with our construction of the Schrodinger equation for a single particle, the Schrodinger equation for our two particles becomes

       (2)      

 

The solution can be written as a product of the wavefunctions for each particle

        (3)      

 

The solution of the Schrodinger equation for a particle in a box is

        (4)    

 

Therefore, a solution Schrodinger equation for our two particles in a box on can be expressed as

       (5)    

 

The energy E of the state for quantum numbers  is given by

      (6)   

 

How do we interpret the wavefunction?

The probability of finding particle 1 in a small line length  and at the same time the probability of finding particle 2 in a small line length  is

      (7)   

 

For the state (2, 3), in a very small interval , the probability density of finding particle 1 at position  and particle 2 at  is

           

 

Now, we can calculate the probability density of finding particle 2 at position  and particle 1 at

        

 

The problem is this, we have assumed that the particles are identical.  We can’t tell which is which, and nobody else can either.  The indistinguishability of elementary particles is not like that of apparently identical macroscopic objects, where one could always place some tiny mark.  There is no way to mark an electron.  This means that the best we can do is to talk about the probability of finding one electron at position  and another at position , we cannot specify which electron we find where.  Therefore, any alleged wavefunction that gives different probabilities for finding the particle at  and another at  is not physically meaningful even though the wavefunction is a solution of the Schrodinger equation. Therefore, a wavefunction describing two identical particles must have a symmetric probability distribution

      (8)      

 

From the above example

                

 

Therefore, the wavefunction given by equation 5 is not a physically meaningful wave function for two identical particles in a one-dimensional box.

 

However, this problem can be easily fixed by having different linear combinations of wavefunction given by equation 5 that form symmetric or antisymmetric wavefunctions that satisfy the Schrodinger equation, have the same energy E and satisfy the requirements when the two particles are swapped around.

 

Symmetric Function

     (9A)       

 

Antisymmetric Function

     (9B)       

 

Both symmetric and antisymmetric wavefunctions arise in nature in describing identical particles. All elementary particles are either fermions, which have antisymmetric multiparticle wavefunctions, or bosons which have symmetric wavefunctions.  Electrons, protons and neutrons are fermions; photons, alpha particles and helium atoms are bosons. 

It is important to realize that this requirement of symmetry of the probability distribution, arising from the true indistinguishability of the particles, has a large effect on the probability distribution, and, furthermore, the effect is very different for fermions and bosons.  This can be shown by plotting the probability distribution functions for symmetric and antisymmetric states and then comparing them.

 

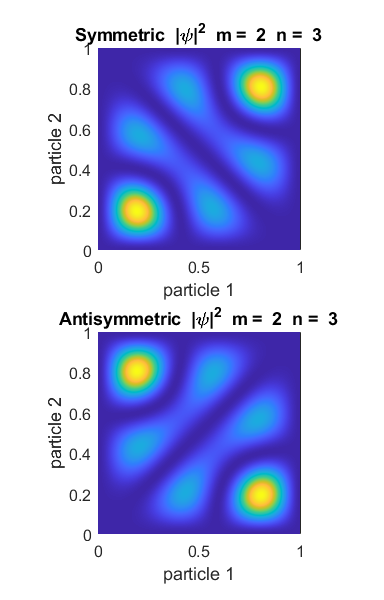
The Script qmTwo.m is used to plot the probability density functions for our two particles confined in the box so that you can compare the plots for symmetric and antisymmetric states for different values of m and n. Figure 1 shows the example for m = 2 and n = 3.

 

        Fig. 1.  Symmetric and antisymmetric states for m = 2 and n = 3.

 

The probability density functions are very different. For the symmetric state, the highest probability is that the two particles are close together (x1 = x2 = 0.2 and x1 = x2 = 0.8). Such particles are called bosons.

 

However, for the antisymmetric case, the particles are most likely to be found far from each other. In fact, there is zero probability that they will be found at the same spot, because  . Thus, two fermions cannot be in the same quantum state. This is the Pauli Exclusion Principle — it is the basis of the periodic table, and consequently of almost everything else.

 

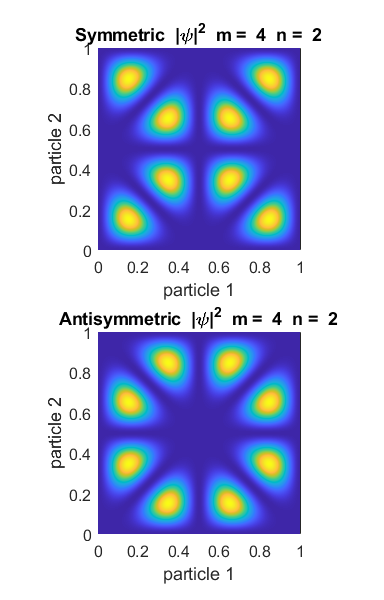
The plots below show states with different quantum numbers. For each symmetric state it is most likely that the particles will be close together and far apart for antisymmetric states.