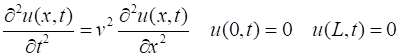DOING PHYSICS WITH MATLAB

 

Ian Cooper

matlabvisualphysics@gmail.com

 

WAVE MOTION

FREQUENCY SPECTRUM OF AN EXCITED STRING

THE WAVE EQUATION AND FOURIER TRANSFORM

 

 

DOWNLOAD DIRECTORIES FOR MATLAB SCRIPTS

 

       Google drive

 

       GitHub

 

em_swe_01A.m

 

The [1D] wave equation can be solved numerically using a finite difference method for the vibrations of a string with given boundary conditions

 

                  

 

where  is the transverse displacement of the string of length L with nodes at each end.

The string is initially excited by random fluctuations along its length. The string can also be clamped at any point xc  .  Points along the string oscillate and the frequency spectrum of any point xf can be computed from the Fourier Transform of the displacement function . To find the frequency spectrum, it is not necessary to use the fast Fourier transform method (FFT). It is much simpler to evaluate the Fourier integral using the function simpson1d.m.

 

The Script em_swe_01A.m is used to solve the wave equation for the transverse displacement function . The time evolution of three points is computed and displaced graphically.

Input:

% Number of spatial grid points

  Nx = 201;

% Number of time steps

  Nt = 2201;

% length of simulation region

   L = 10;

% wave or propagation speed

   v = 20;

% Courant number

   S = 1;

% Thee signal detection location SL / Clamped string location CL  (indices)

  SL = round([Nx/2, Nx/3,Nx/4]);

  CL = round([Nx/3 2*Nx/3]);

  %  CL = 1;

Setup:

% Spatial grid spacing / time step / spatial grid

   hx = L / Nx;

   ht = S * hx / v;

   S2 = S^2;

   x = linspace(0, L , Nx);

   t = linspace(0,ht*Nt,Nt);

 

% Random initial conditions   (comment / uncomment rand # selection

   u = zeros(Nx,Nt);

  % u(2:Nx-1,1) = 0.25.*rand(Nx-2,1);

     u(2:Nx-1,1) = 1 .* (2.*rand(Nx-2,1) - 1);

 

Finite Difference Time Development Method – solving the wave equation:

for nt = 2 : Nt-1

    for nx = 2 : Nx-1

        u(nx,nt+1) = 2*u(nx,nt)- u(nx,nt-1)+ S2*(u(nx+1,nt) - 2*u(nx,nt) + u(nx-1,nt));

% Clamped location   (comment / uncomment    

        u(CL,nt+1) = 0;

    end

% Boundary Conditions    comment / uncomment

      u(1,  nt+1)  = 0;               % Fixed end

      u(Nx, nt+1) = 0;               % Fixed end

end

 

FOURIER TRANSFORM

% Frequency range

  fMax = 10;

  f = linspace(0,fMax,Nt);

% Initialize F.T. 

%  HB = zeros(1,Nt); HR = zeros(1,Nt); HM = zeros(1,Nt);

 

  HB = FT(u(SL(1),:),f,t,Nt);

  psdB = HB.*conj(HB);

 

  HR = FT(u(SL(2),:),f,t,Nt);

  psdR = HR.*conj(HR);

 

  HM = FT(u(SL(3),:),f,t,Nt);

  psdM = HM.*conj(HM);

 

function  H = FT(u1,f,t,Nt)

  H = zeros(Nt,1);

 % Fourier Transform H(f)

  for c = 1:Nt

   g = u1 .* exp(1i*2*pi*f(c)*t);

   H(c) = simpson1d(g,min(t),max(t));

 end

 

 

 SAMPLE RESULTS

L = 10  m     v = 20 m.s-1     fundamental:  f = 1.00 Hz   T = 1.00 s     = 20 m

 

String only clamped at its end

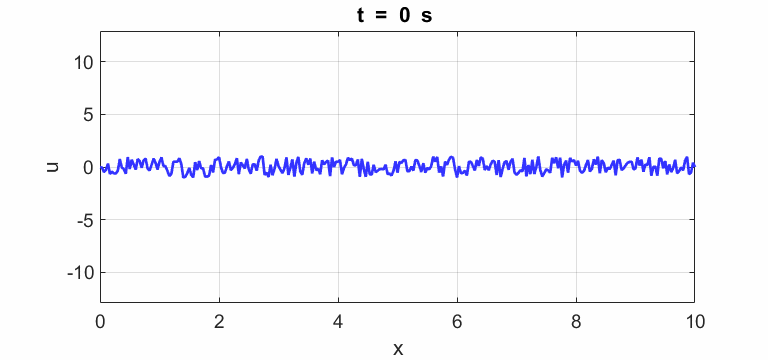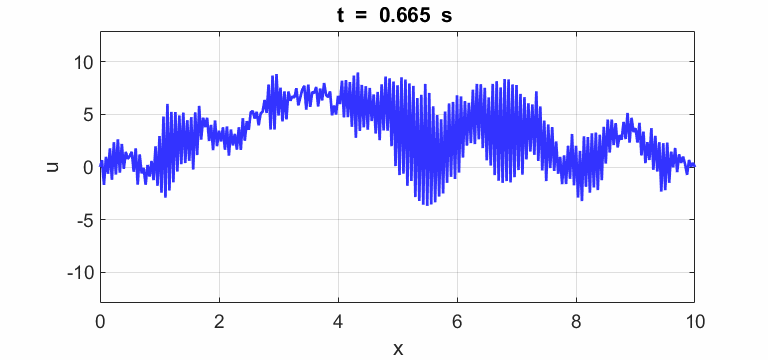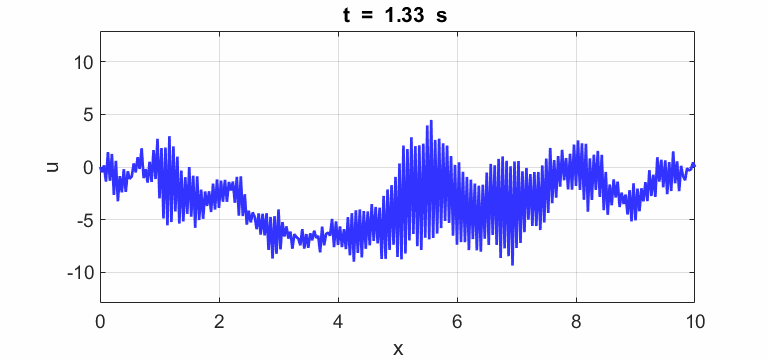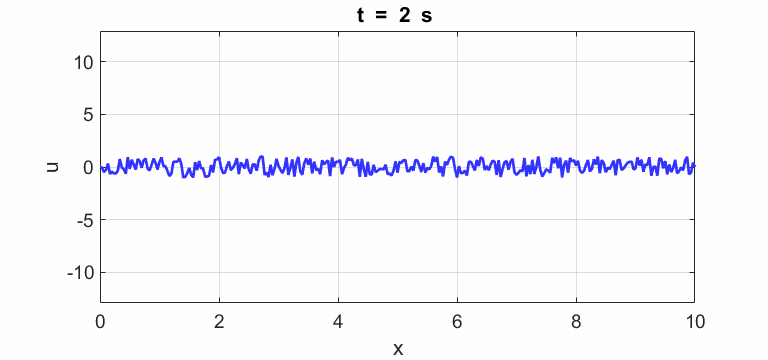
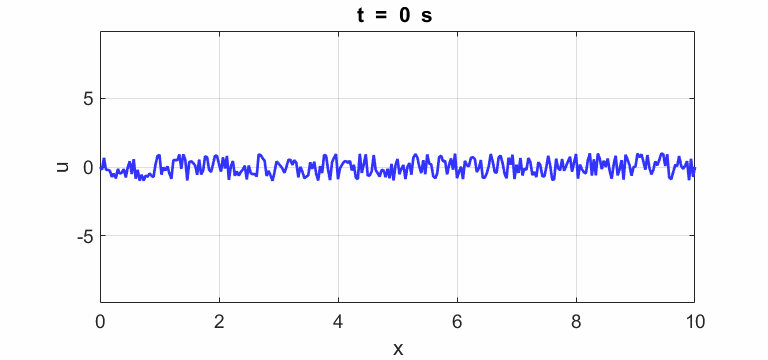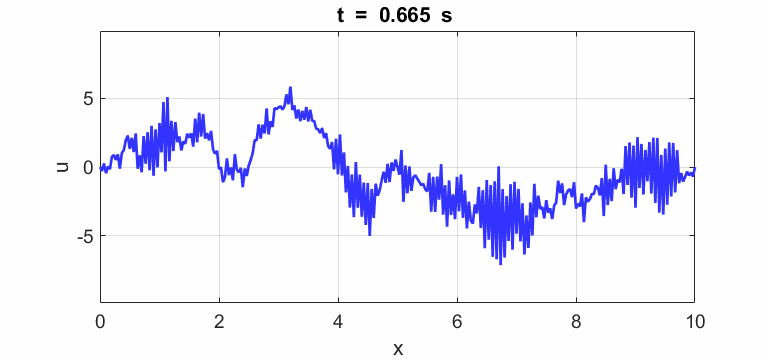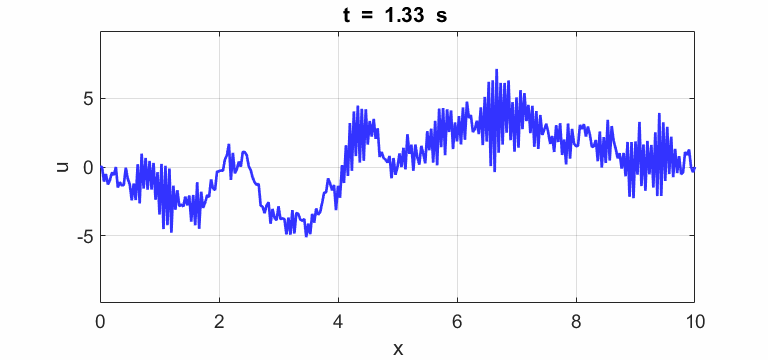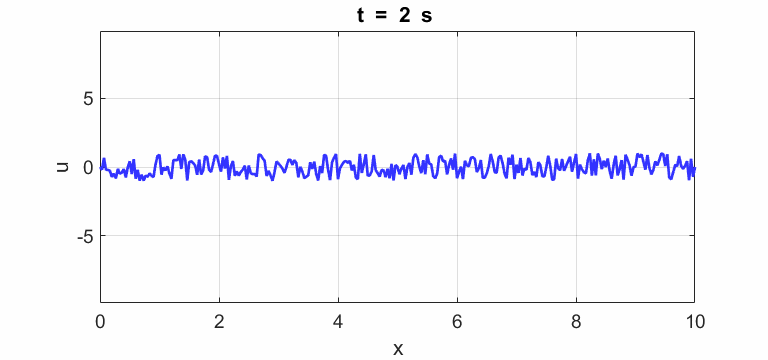
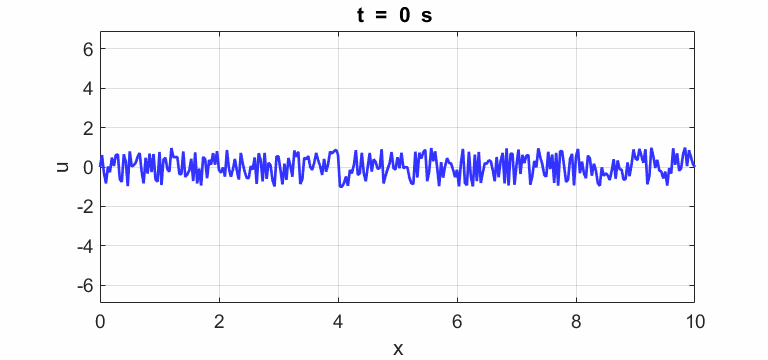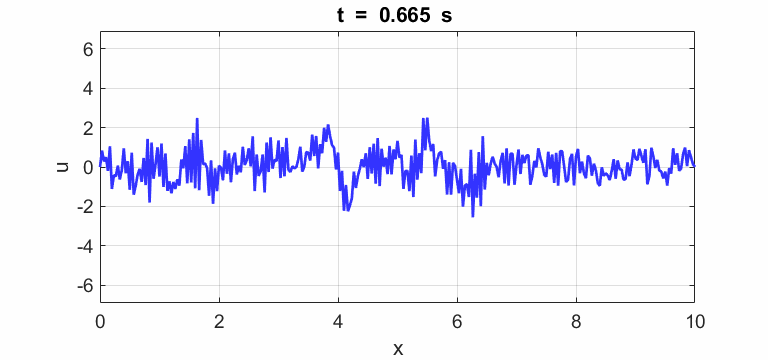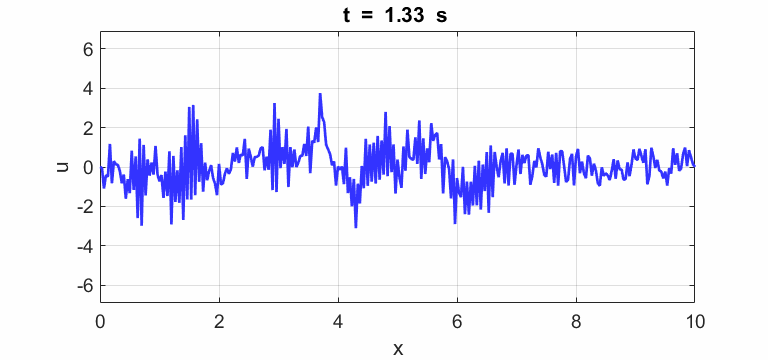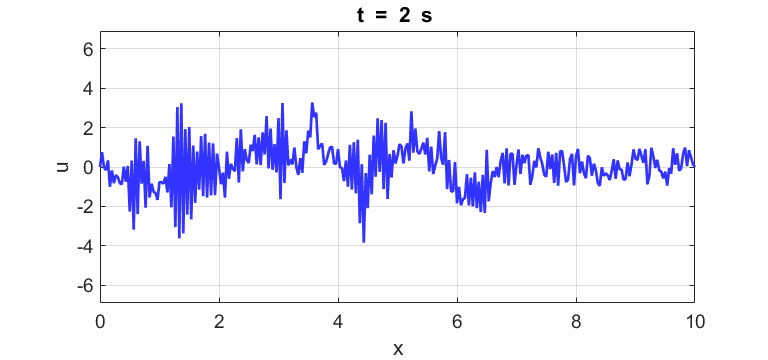
            Transverse displacement of string

             (u(2:Nx-1,1) = 1 .* (2.*rand(Nx-2,1) - 1);)

 

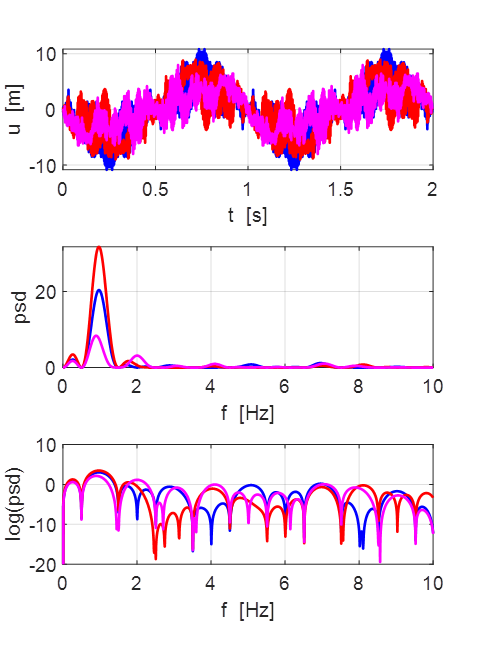
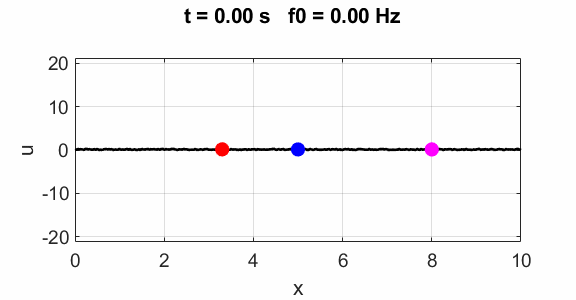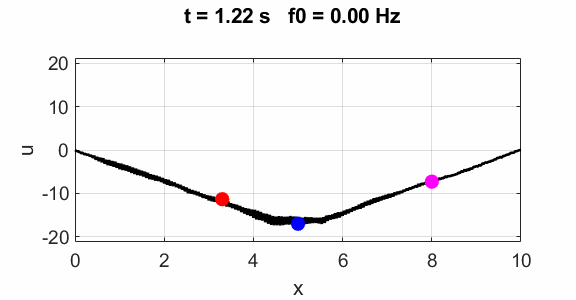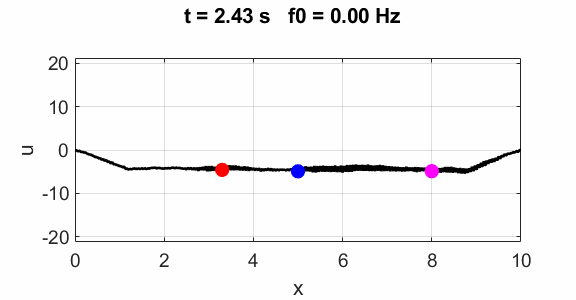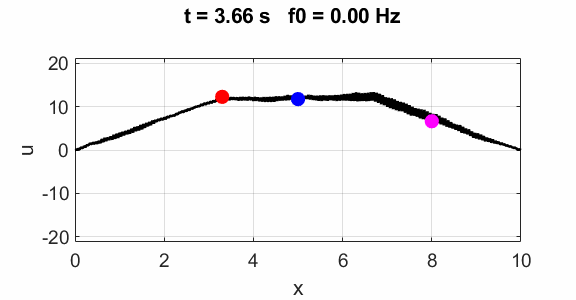
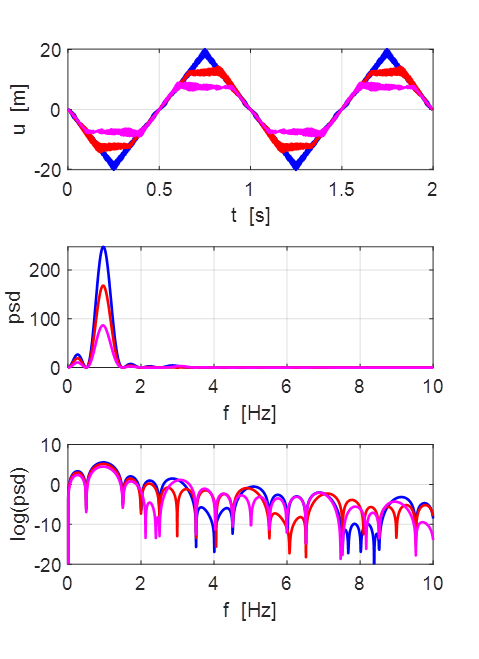
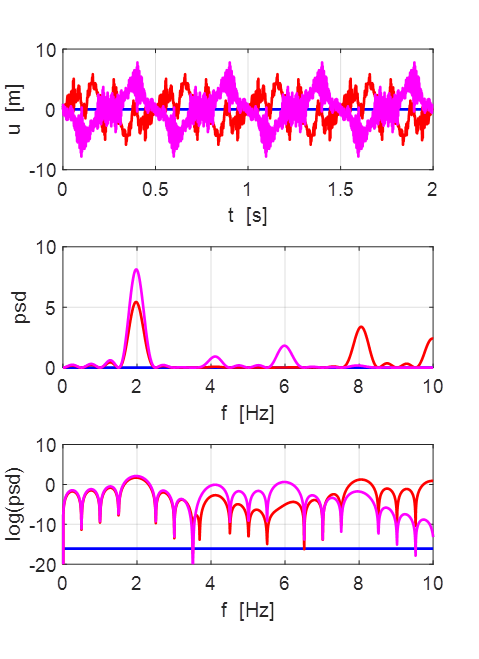
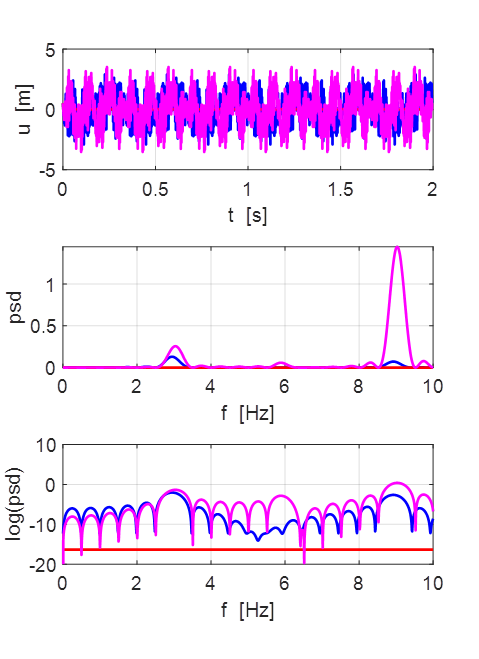
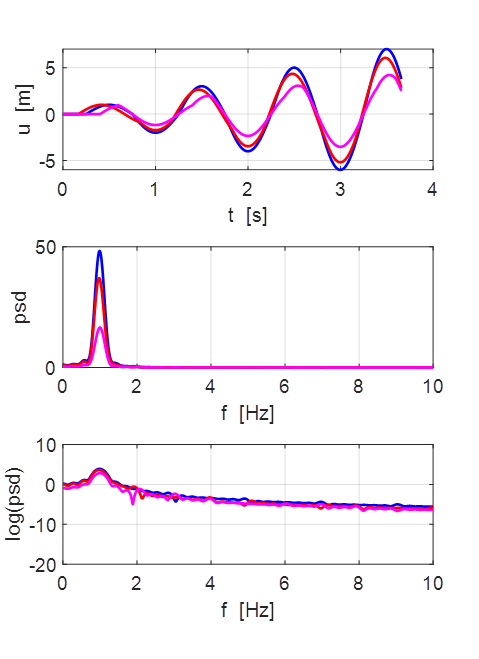
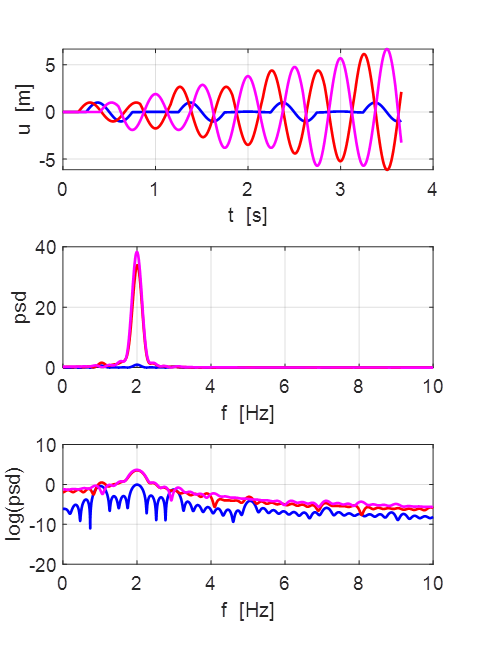
               Oscillations at x = L/2 (blue), x = L/3 (red) and x = L/4 (magenta).

               All three points oscillate with the predominant frequency component equal to

              the fundamental frequency of 1.00 Hz. The oscillations are not sinusoidal.

              (u(2:Nx-1,1) = 1 .* (2.*rand(Nx-2,1) - 1);)

 

 

            Transverse displacement of string

      u(2:Nx-1,1) = 0.25.*rand(Nx-2,1);

 

             Oscillations at x = L/2 (blue), x = L/3 (red) and x = L/4 (magenta).

             All three points oscillate with the predominant frequency component equal to

             the fundamental frequency of 1.00 Hz. The oscillations are not sinusoidal.

      u(2:Nx-1,1) = 0.25.*rand(Nx-2,1);

 

 

String clamped at x = L/2

                Transverse displacement of string

                (u(2:Nx-1,1) = 1 .* (2.*rand(Nx-2,1) - 1);)

 

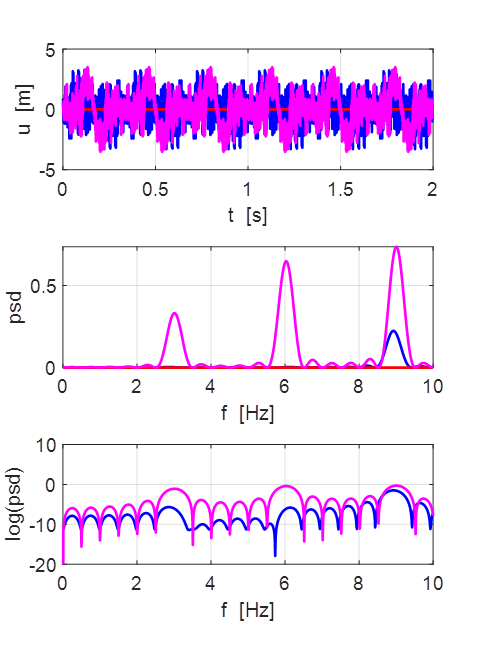
               Oscillations at x = L/2 (blue), x = L/3 (red) and x = L/4 (magenta).

              At x = L/2 there is a node since the string is clamped at this position.

              The even harmonics are mainly excited with the peak in the spectrum

              occurring at the frequency of the 2rd harmonics.

              (u(2:Nx-1,1) = 1 .* (2.*rand(Nx-2,1) - 1);)

 

 

String clamped at x = L/3 and x = 2L/3

                 Transverse displacement of string       

                 (u(2:Nx-1,1) = 1 .* (2.*rand(Nx-2,1) - 1);)

 

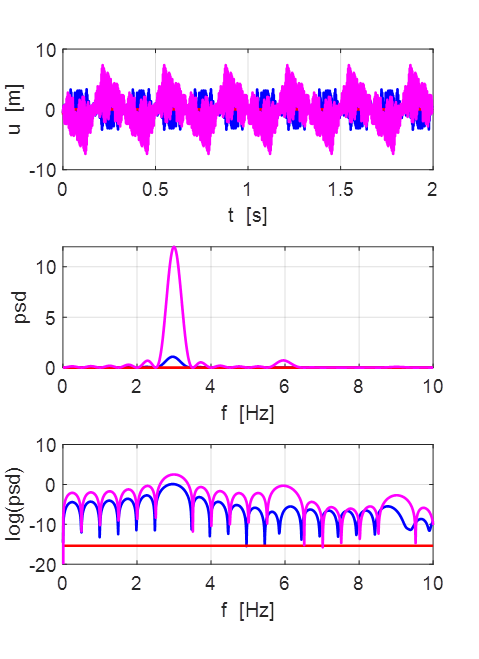
               Oscillations at x = L/2 (blue), x = L/3 (red) and x = L/4 (magenta).

               At x = L/3 there is a node since the string is clamped at this position.

              The other two points oscillate almost at the frequency of the 3rd harmonics.

              The main frequency components excited ate the harmonics 3, 6, 9. Each time

              The Script is run, the distribution of energy into the harmonics 3, 6, 9 is different.

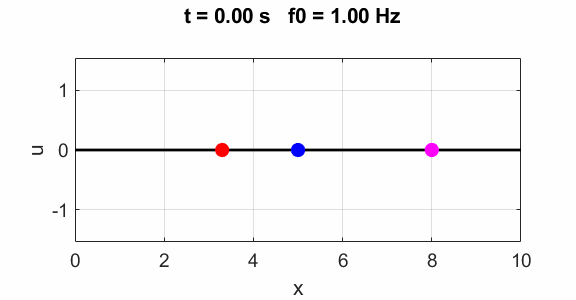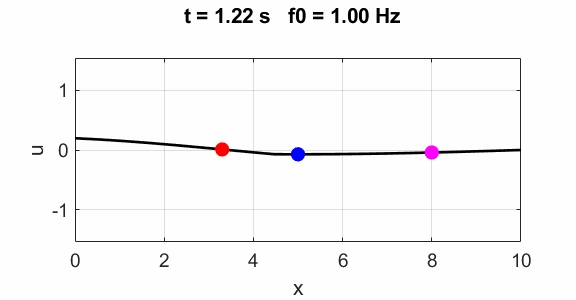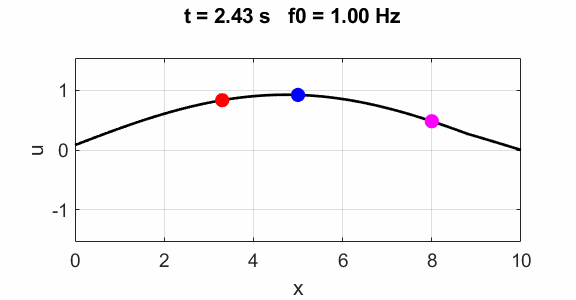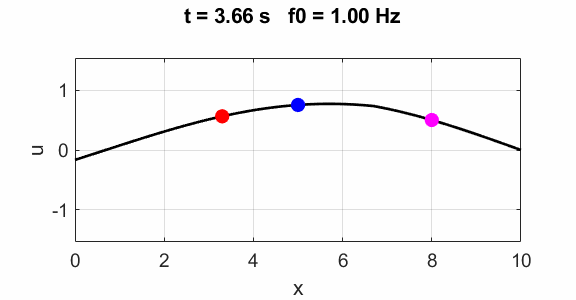
              (u(2:Nx-1,1) = 1 .* (2.*rand(Nx-2,1) - 1);)

 

Natural frequencies of oscillation: Driven string

The Script can be modified by commenting and uncommenting the code to excite the string at x = 0 by a sinusoidal signal with frequency f0.

for nt = 2 : Nt-1

    for nx = 2 : Nx-1

    % sinusoidal excited at x = 0;

      u(1,nt+1) = 1*sin(2*pi*f0*t(nt));

        u(nx,nt+1) = 2*u(nx,nt)- u(nx,nt-1)+ S2*(u(nx+1,nt) - 2*u(nx,nt) + u(nx-1,nt));

% Clamped location   (comment / uncomment    

%        u(CL,nt+1) = 0;

 

    end

% Boundary Conditions    comment / uncomment

 %     u(1,  nt)  = 0;               % Fixed end

      u(Nx, nt) = 0;               % Fixed end

end

 

Fundamental 1st harmonics  f0 =1

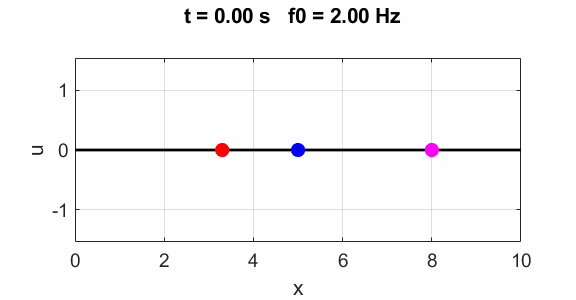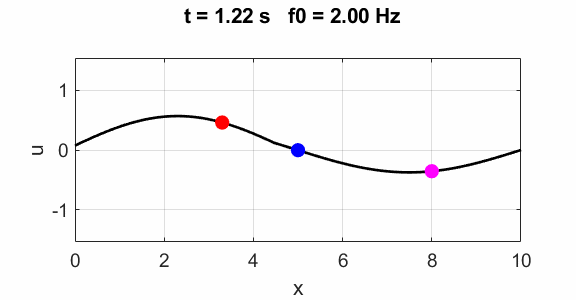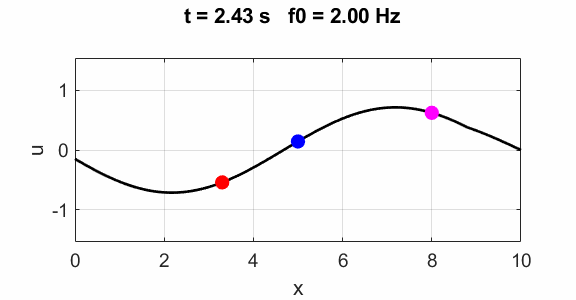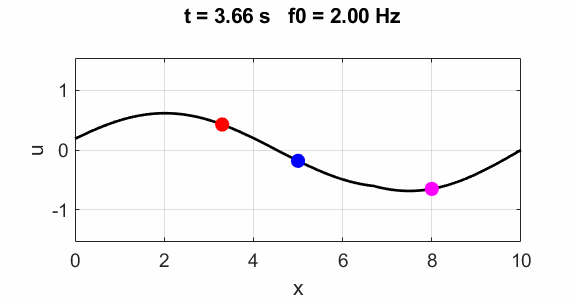
Second harmonic f0 = 2

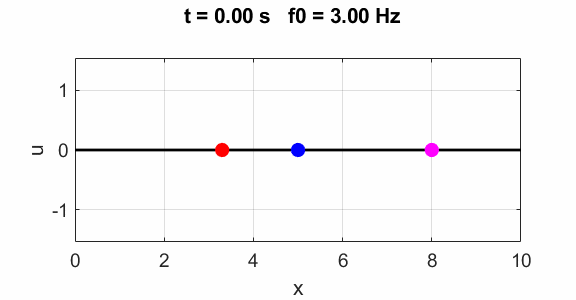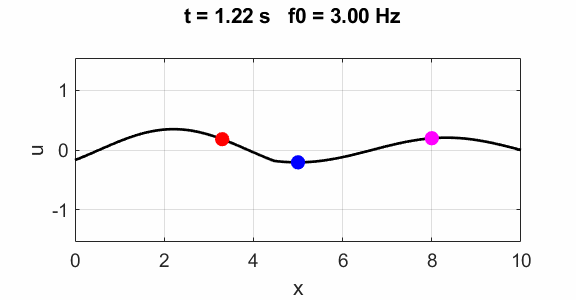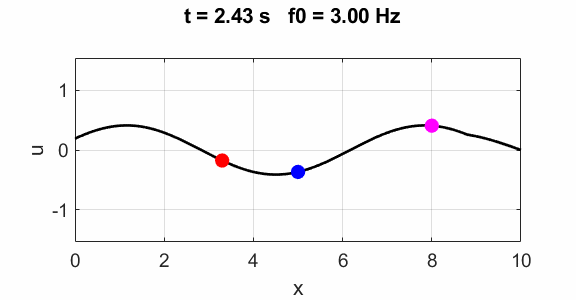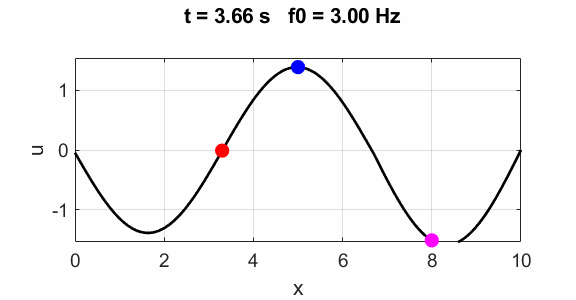
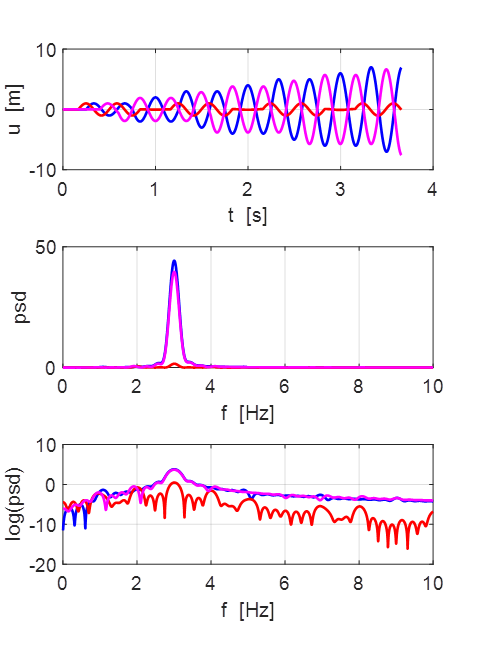
Third harmonics f0 = 3

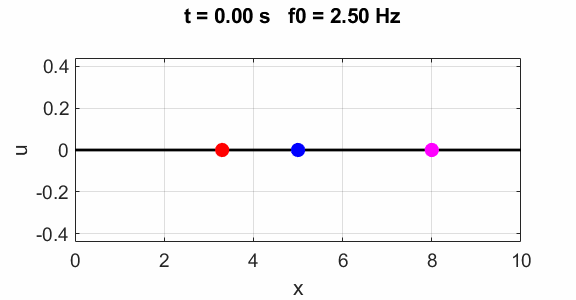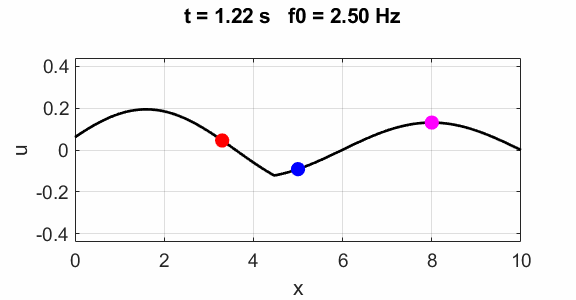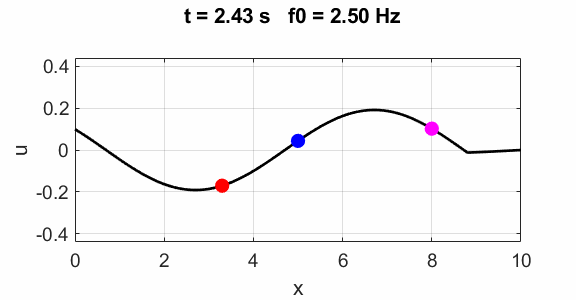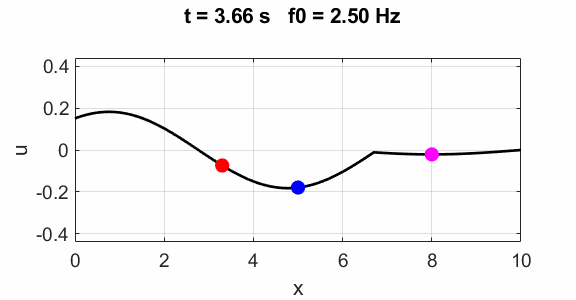
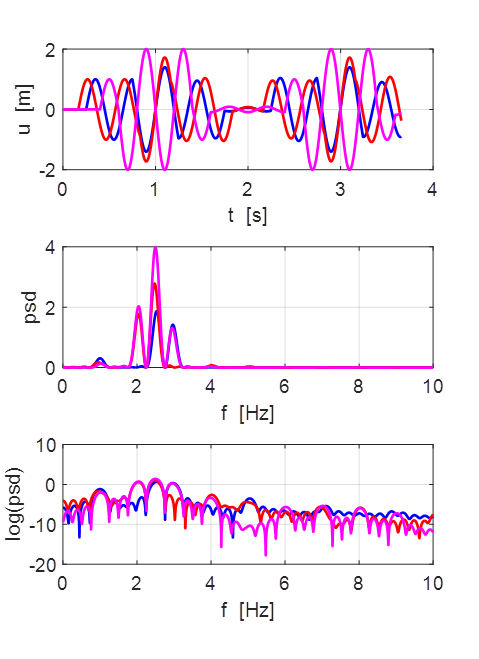
Non-harmonic frequency  f0 = 2.5