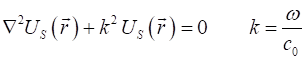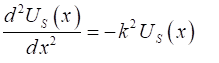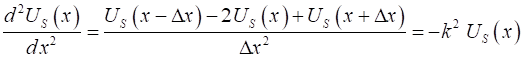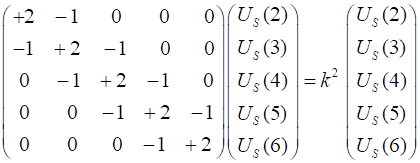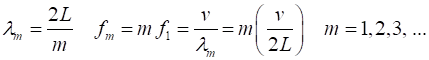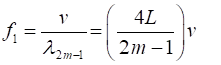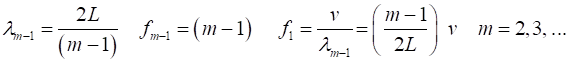DOING PHYSICS WITH MATLAB

 

HELMHOLTZ EQUATION

EIGENVALUE PROBLEM

 TRANSVERSE STANDING WAVES ON A ROD

 

Ian Cooper

Email:  matlabvisualphysics@gmail.com

 

wm_Helmholtz.m

Solution of the Helmholtz equation for the transverse vibrations of a rod with boundary conditions that can be either fixed or free. The modes of vibration of the rod are found by finding the eigenvalues and corresponding eigenfunctions for the Helmholtz equation expressed in matrix form. The INPUT section of the Script is used to enter the boundary conditions, number of time steps, number of spatial grid points, the length of the rod, the transverse wave velocity and the mode of vibration for the standing wave. The animated motion can be saved as an animated gif file by setting flagS = 1. The script could be altered so the animation could be saved as an avi file and the input parameters entered via the Command Window or using the Live Editor. 

 

Link to Script

 

https://github.com/D-Arora/Doing-Physics-With-Matlab/blob/master/mpScripts/wm_Helmholtz.m

 

 

THE HELMHOLTZ EQUATION

 

The Helmholtz equation is

     (1)    

 

where  is the spatial wave function (or wavefunction) and we will only consider the case where k is a constant. It is a second-order differential equation that appears in quantum mechanics, electromagnetism, wave phenomena, among others.

 

The Helmholtz equation represents a time-independent form of the wave equation and results from applying the technique of separation of variables to reduce the complexity of the analysis.

     (2)    

 

It is often convenient to assume that the wavefunction  varies harmonically (sinusoidal variation with time), so the wavefunction can be expressed the product of a spatial wavefunction  and a harmonic time-varying function

 

      (3)    

 

By substitution of equation 3 into equation 2, we can derive the Helmholtz equation

     (1)    

 

 

The [1D] form of the Helmholtz equation is

      (4)    

 

The solution of the Helmholtz equation depends upon the boundary conditions applied to the system.

 

 

STANDING TRANSVERSE WAVES OF A ROD

 

The motion of oscillating systems is a classic problem in eigenvalue theory which we can easily investigate using Matlab. For example, we can model the complex oscillations of the Tacoma Narrows Bridge in which the deck of the bridge undergoes two kinds of vibration: one along its length and the other from side-to-side.

 

Fig. 1.  Vibrations along the length of the bridge. Boundary conditions: fixed / fixed (nodes at the ends of the bridge span).

 

Fig. 2. Side-to-side vibrations. Boundary conditions: free / free (antinodes along the side of the bridge span).

 

 

We can approximate the second derivative by the finite difference approximation to give

 

     (5)      

 

 

Let the X-domain be divided into  grid points (1, 2, … , N,, N+2) where the spacing between grid points is . Therefore, the length of the X-domain is . We then apply our approximation given in equation 5 at each interior grid point (2, 3, 4, … , N) to approximate equation 4 and express the result in matrix form.

 

For example, if N = 5 and the boundary conditions at the ends are , then

       (6)        

 

 

 

since

          

           

            . . .

         

 

We now have a simple eigenvalue problem of the form

         

 

where  is the eigenvalue and  is the eigenfunction.

 

We are now able to solve equation 6 using the following Matlab code

 

% Eigenvalue Matrix A: eigenfunctions (eignFN) / eigenvalues (eignV)

  off = ones(N-1,1);

  A = 2*eye(N) - diag(off,1) - diag(off,-1);

  

  [eignFN, eignV] = eig(A);

 

% Spatial Wavefunction US for mode m

  US = zeros(N+2,1);

  US(2:N+1) = eignFN(:,m);

  US = US ./max(US);

 

The length of the rod is  and its actual physical length is L. So, we need to scale the X-domain, via

% Spatial domian  [m]

  x = (0:N+1).*(L/(N+1));

 

k is the propagation constant and it needs to be scaled to express its value in rad.s-1.

% propagation constant  [1/m]

  k = sqrt(eignV(m,m)) .* (N+1)/L;

 

The value of the propagation constant k and the transverse wave speed v are used to calculate the wavelength , angular frequency , period T and frequency f  for the normal mode of vibration m. Hence, we can calculate the harmonic time dependence part of the wave function

 

  % angular frequency  [rad/s]

    w = v*k;

  % period  [s]

    T = 2*pi/w;

  % frequency  [Hz]

    f = 1/T;

  % time  [s]

    t = linspace(0,2*T,nT);

  % wavelength [m]

    lambda = 2*pi/k;

  % time dependent wavefunction  

    UT = cos(w.*t);  

 

To examine different modes of vibration, the Script is run with different values of the mode number m.

 

So far, we have only considered nodes at each end of the rod. We can also model the vibrations of the rod with an antinode at the ends (free). Equation 5 can be written as

           

 

   Antinode (free) at left end of rod     

           

 

Therefore, in the matrix A element A(1,1) = 1.

 

   Antinode (free) at the right end of the rod     

           

 

Therefore, in the matrix A element A(N+1,N+1) = 1.

 

In the Script, the boundary conditions are set by the variable BC

 

% Boundary conditions: fixed fixed BC = 1 / fixed free BC = 2 / free free BC = 1

  BC = 1;

 

  if BC == 2; A(N,N) = 1; end               % fixed free

  if BC == 3; A(1,1) = 1; A(N,N) = 1; end   % free free

 

  if BC == 2; US(N+2) = US(N+1); end

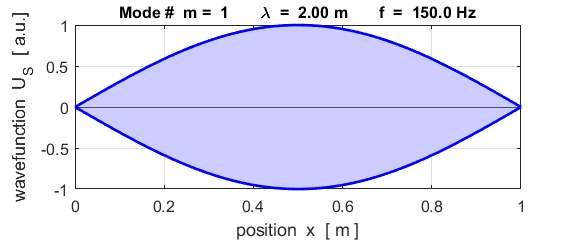
  if BC == 3; US(1)   = US(2); US(N+2) = US(N+1); end

 

Note: The matrix A does not include the end grid points related to the X-domain, but only the N interior grid points.

 

 

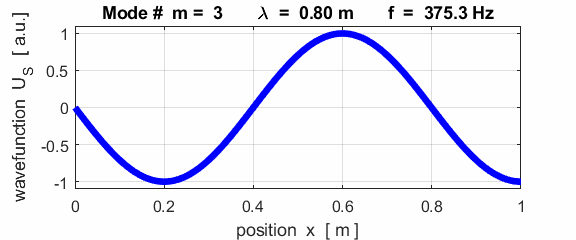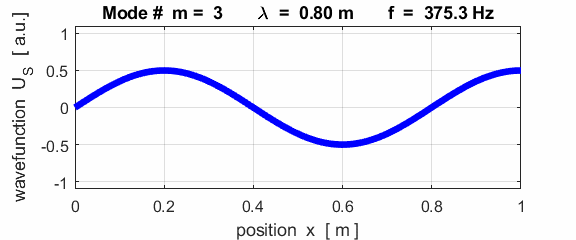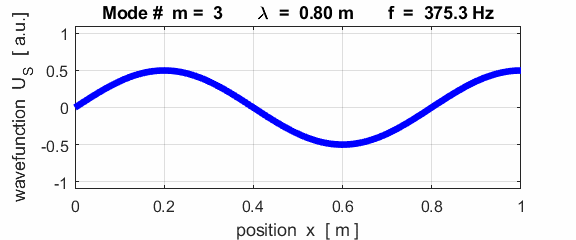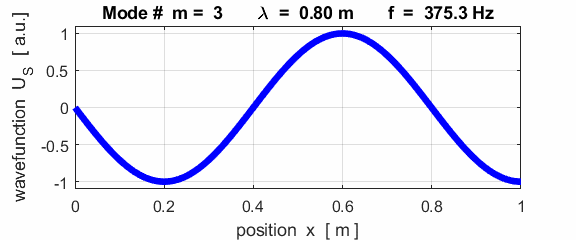
Boundary conditions: nodes at each end of the rod (fixed / fixed)

 

 

 

This mode of vibration is like the oscillations of the Tacoma Bridge span along its length (figure 1).

 

 

 

 

 

 

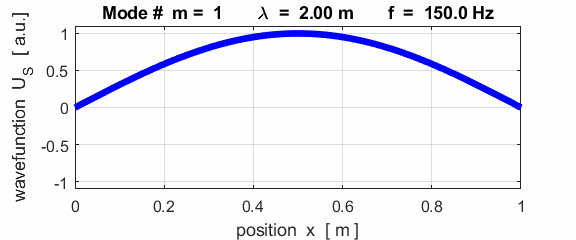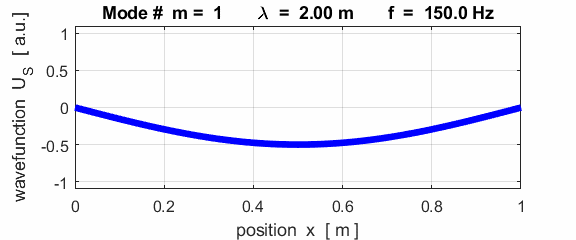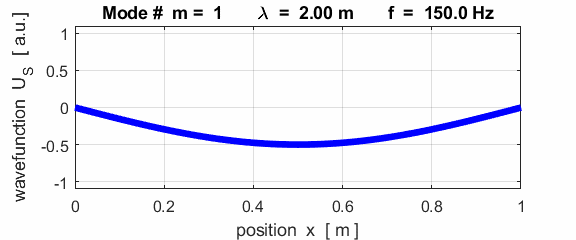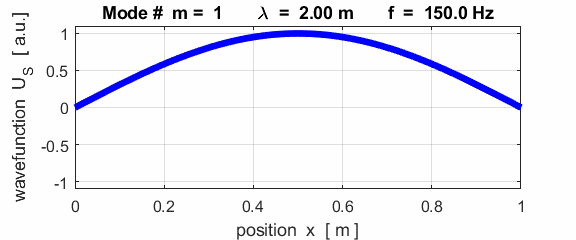
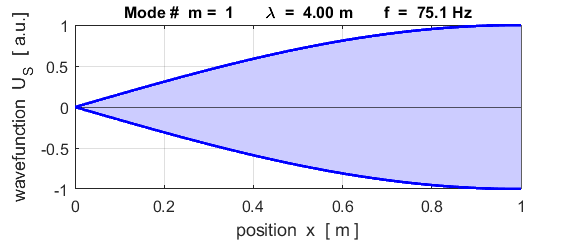
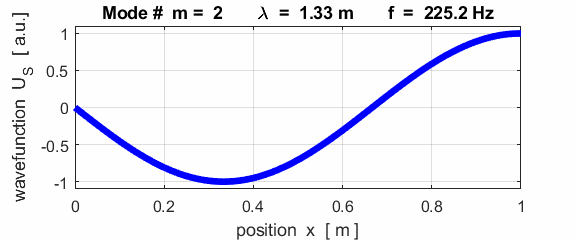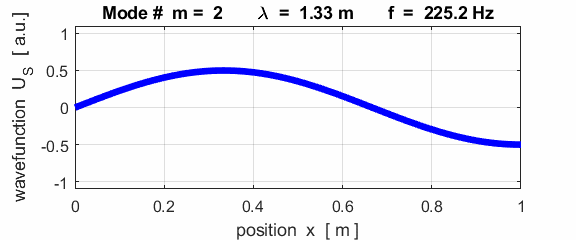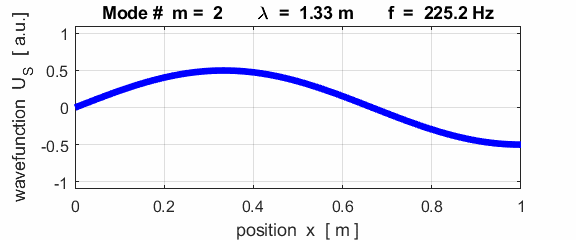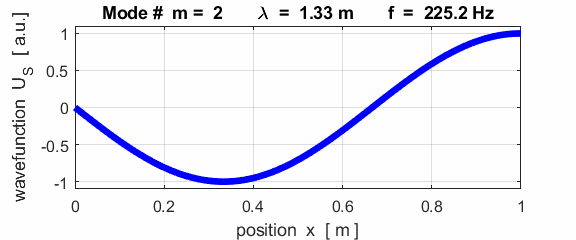
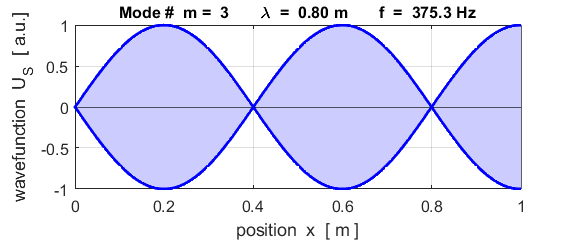
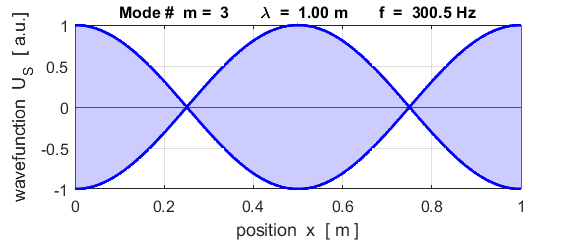
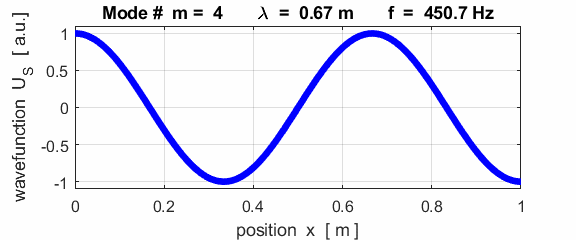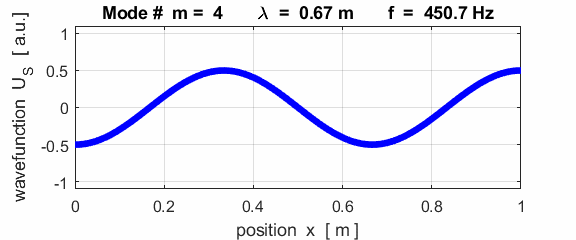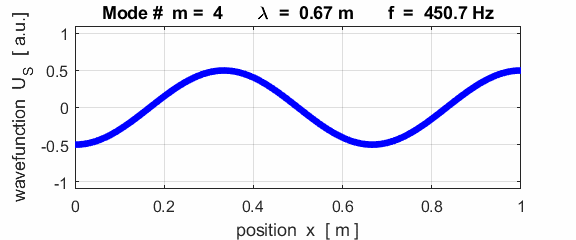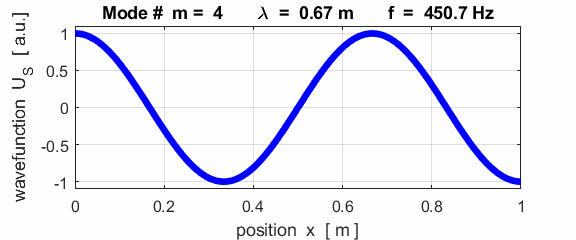
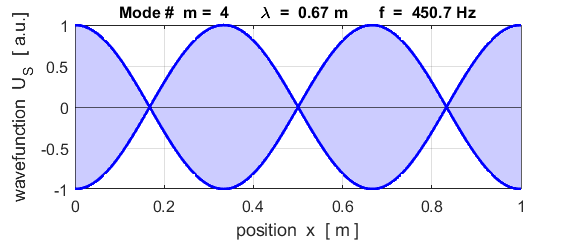
The mode m = 1 is called the fundamental or 1st harmonic mode of vibration.

For the rod fixed at both ends (nodes at each end), the results of the simulations show that

          

      

where  and  are the wavelength and frequency of the mth harmonic respectively.

 

For the rod fixed at both end, all the harmonics can be excited.

 

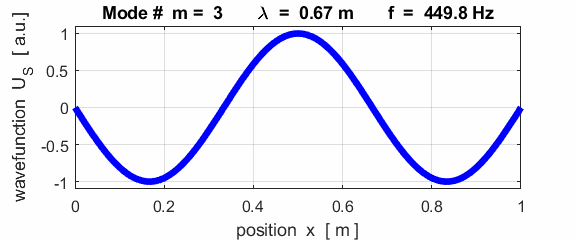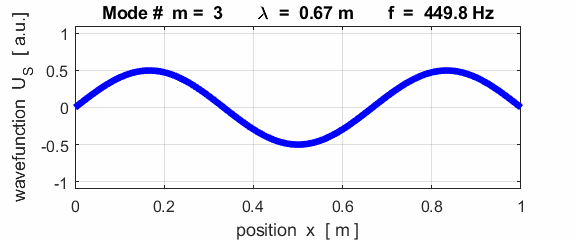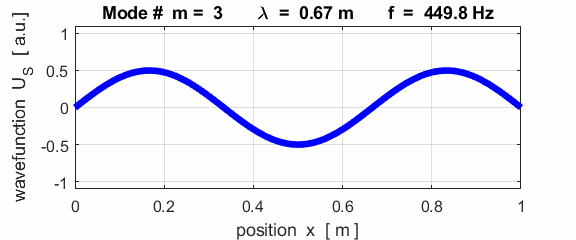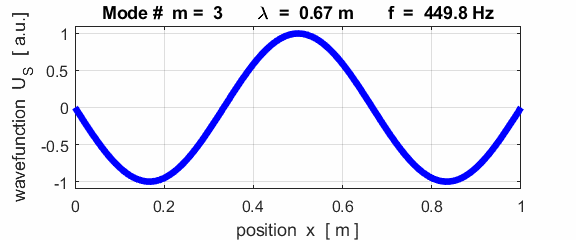
Note: The wavelength  of a normal mode of vibrations is determined by the length L of the rod and the mode number m. The frequency f  is determined by the transverse wave velocity v, the length L of the rod and the mode number m.

 

 

 

Boundary conditions: node at left and an antinode at the right end

                                    (fixed / fixed)    BC = 2

 

 

 

 

 

 

 

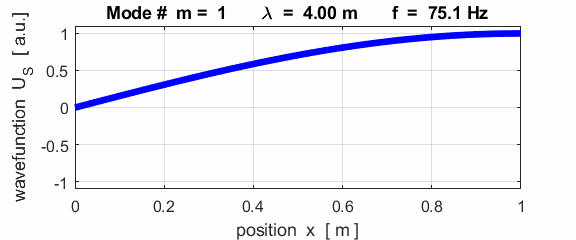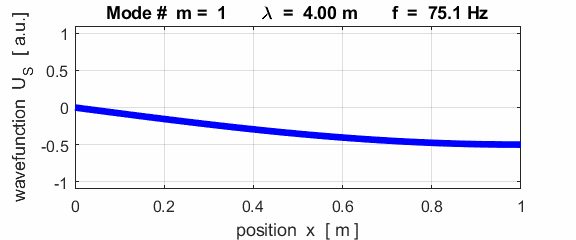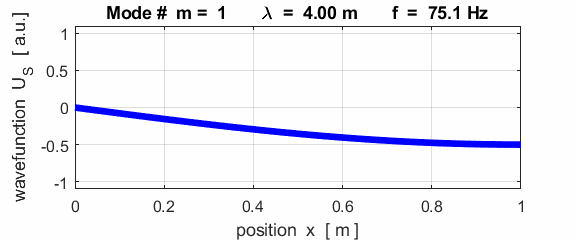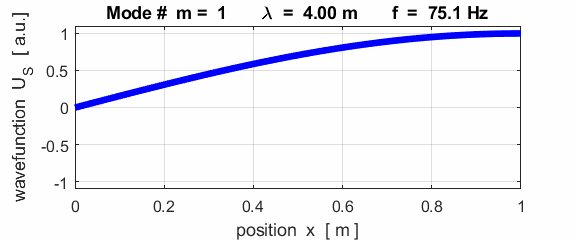
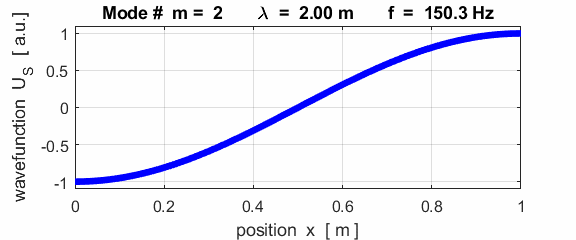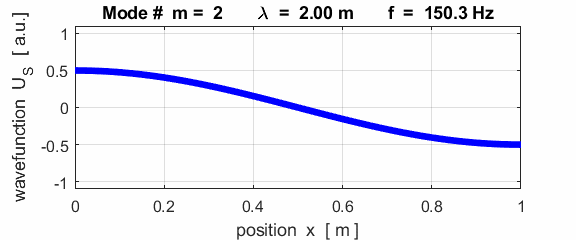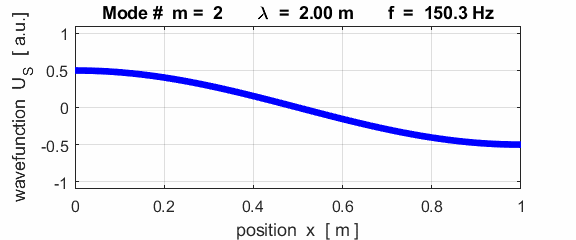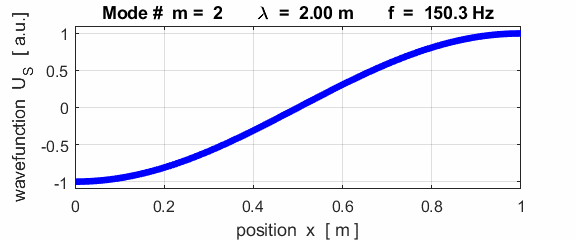
For the rod with a node at the left end and an antinode at the right end (fixed / free), the results of the simulations show that

          

          

 

 

 

For the rod with the fixed / free boundary conditions, only the odd harmonics can be excited.

 

 

Boundary conditions: antinode at both ends (fixed / fixed)    BC = 3  (m>1)

 

 

 

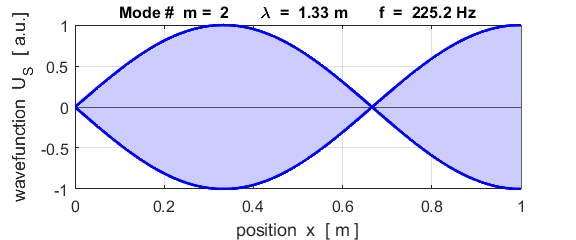
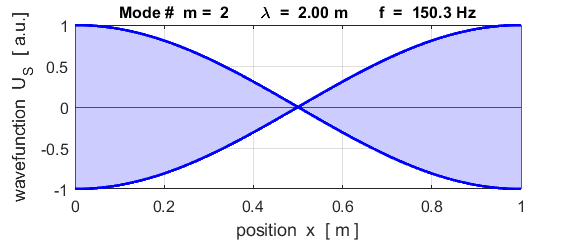
This mode of vibration is like the side-to-side oscillations of the Tacoma Narrows Bridge (figure 2).

 

 

 

 

 

 

 

For the rod with an antinodes at both ends of the rod (free / free), the results of the simulations show that

          

 

 

For the rod with the free / free boundary conditions, all the harmonics can be excited.

 

 

The Script wm_Helmholtz.m can be easily modified to model the vibrations of air columns in tubes or standing electromagnetic waves. The same equation and solution procedure is exactly the same for many very different physical situations involving standing waves.