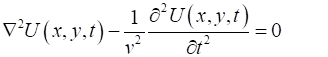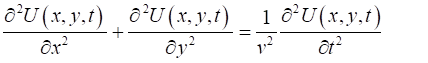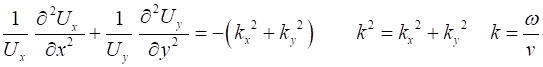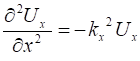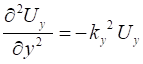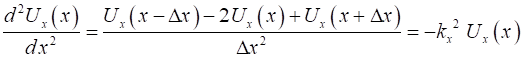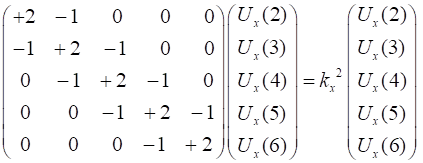DOING PHYSICS WITH MATLAB

 

HELMHOLTZ EQUATION

EINGENVALUE PROBLEM: A VIBRATING MEMBRANE

 

DOWNLOAD DIRECTORY FOR MATLAB SCRIPTS

 

wm_Helmholtz2D.m

Solution of the Helmholtz equation to model the vibrations of a rectangular membrane which has a node around its perimeter. The modes of vibration of the membrane are found by finding the eigenvalues and corresponding eigenfunctions for the Helmholtz equation expressed in matrix form. The INPUT section of the Script is used to enter the number of time steps, number of spatial grid points, the dimensions of the membrane, the transverse wave velocity and the mode of vibration for the standing wave. The animated motion can be saved as an animated gif file by setting flagS = 1. The Script could be altered so the animation could be saved as an avi file and the input parameters entered via the Command Window or using the Live Editor. 

 

 

 

THE HELMHOLTZ EQUATION

 

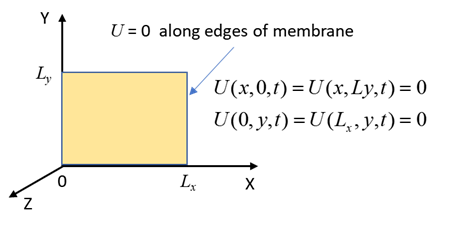
Let’s consider a two-dimensional example of the standing waves in an elastic membrane. If the rest position for the membrane is the X-Y plane, so when it’s vibrating it’s moving up and down in the Z-direction. The shape of the surface at any instant of time is a function is given by the wavefunction . Our goal is to model the vibrations of the surface.

 

     Fig. 1.   Geometry for the vibrating membrane.

 

 The wavefunction must satisfy the [2D] wave equation

 

      (1A)    

 

      (1B)     

 

 

To solve the wave equation 1B, we can use the method of separation of variables where solutions have the form

       (2)       

 

Substituting equation 2 into 1B and dividing the result by  gives

                  

 

The functions of x and y must be independent, therefore

 

       (3A)    

 

       (3B)        

 

 

Equation 3 is the Helmholtz equation and represents a time-independent form of the wave equation.

 

 

STANDING TRANSVERSE WAVES OF A VIBRATING MEMBRANE

 

The motion of oscillating systems is a classic problem in eigenvalue theory which we can easily investigate using Matlab.

 

For the X domain, we can approximate the second derivative by the finite difference approximation to give

 

     (4)      

 

 

Let the X-domain be divided into  grid points (1, 2, … , N,, N+2) where the spacing between grid points is . Therefore, the length of the X-domain is . We then apply our approximation given in equation 4 at each interior grid point (2, 3, 4, … , N) to equation 3 and express the result in matrix form.

 

For example, if N = 5 and the boundary conditions at the ends are , then

       (5)        

 

 

 

 

since

          

           

            . . .

         

 

We now have a simple eigenvalue problem of the form

         

 

where  is the eigenvalue and  is the eigenfunction.

 

For the Y domain, the procedure is identical as given above for the X domain.

 

We are now able to solve equation 5 using the following Matlab code and calculate the natural frequencies of vibration for the normal modes specified by the integers mX and mY.

 

% CALCULATIONS  ======================================================

% Spatial domian  [m]

  x = (0:N+1).*(LX/(N+1));

  y = (0:N+1).*(LY/(N+1));

 

% Eigenvalue Matrix A: eigenfunctions (eignFN) / eigenvalues (eignV)

  off = ones(N-1,1);

  A = 2*eye(N) - diag(off,1) - diag(off,-1);

 

  [eignFN, eignV] = eig(A);

 

% Spatial Wavefunction  US

  USX = zeros(N+2,1);

  USX(2:N+1) = eignFN(:,mX);

  USX = USX ./max(USX);

 

  USY = zeros(N+2,1);

  USY(2:N+1) = eignFN(:,mY);

  USY = USY ./max(USY);

 

  USXX = meshgrid(USX);

  USYY = meshgrid(USY)';

 

  USS = USXX.*USYY;

 

% Time dependent wavefunction UT

  % propagation constant  [1/m]

    kX = sqrt(eignV(mX,mX)) .* (N+1)/LX;

    kY = sqrt(eignV(mY,mY)) .* (N+1)/LY;

    k = sqrt(kX^2 + kY^2);

  % angular frequency  [rad/s]

    w = v*k;

  % period  [s]

    T = 2*pi/w;

  % frequency  [Hz]

    f = 1/T;

  % time  [s]

    t = linspace(0,1*T,nT);

  % wavelength [m]

    lambda = 2*pi/k;

 % time dependent wavefunction  

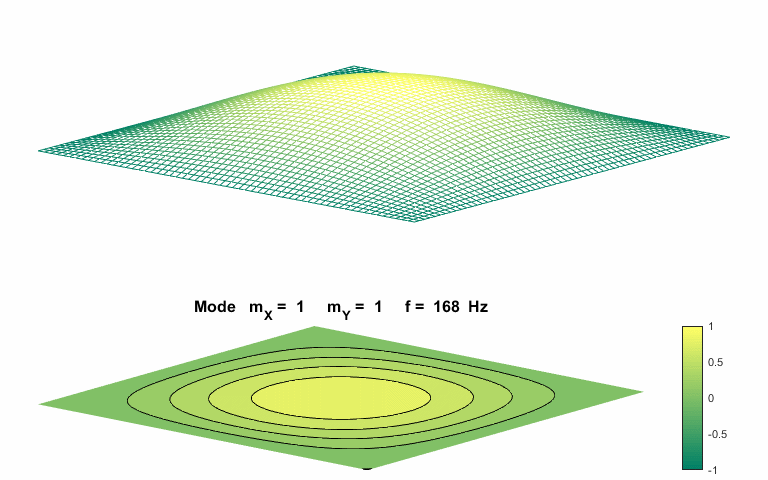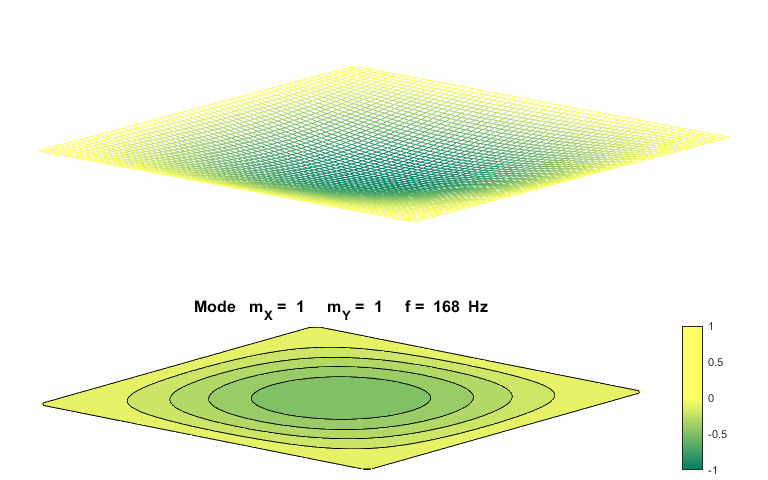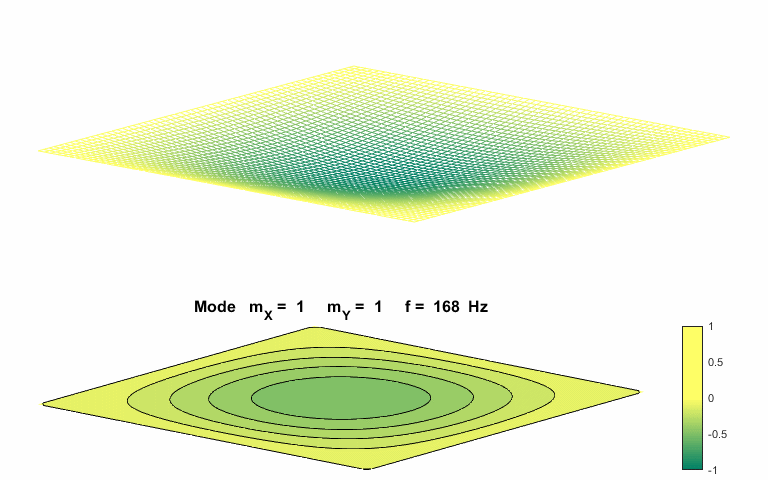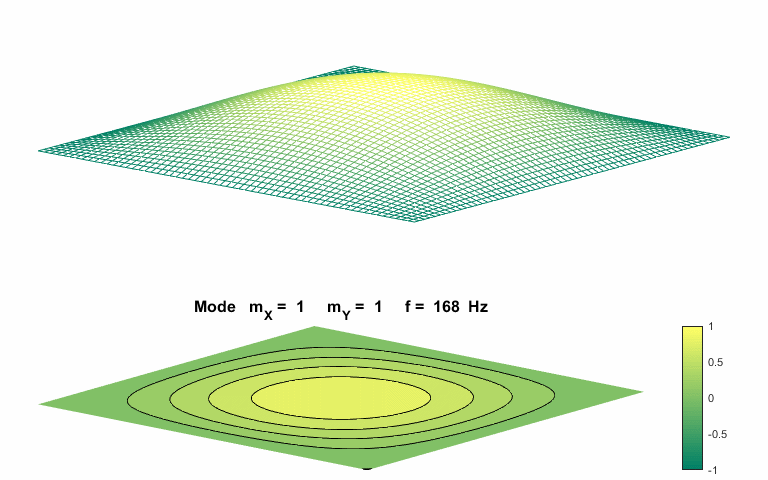
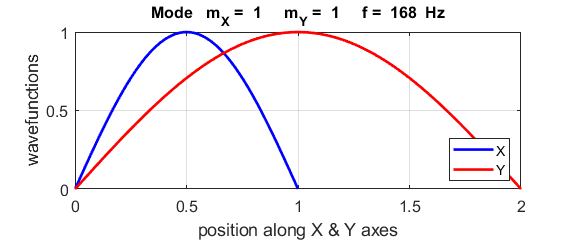
    UT = cos(w.*t);  

 

Fundamental normal mode of vibration mX = 1    mY = 1

 

 

 

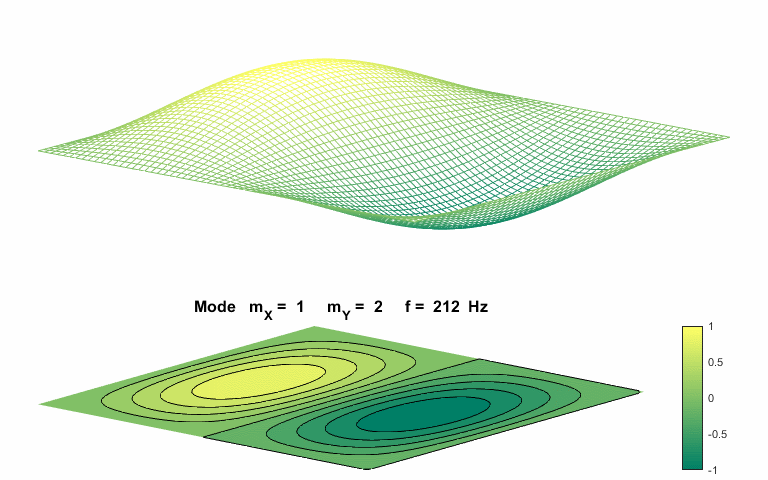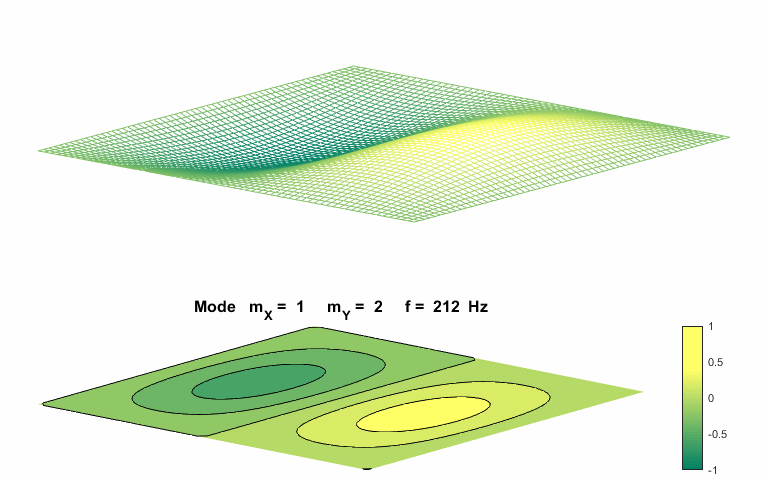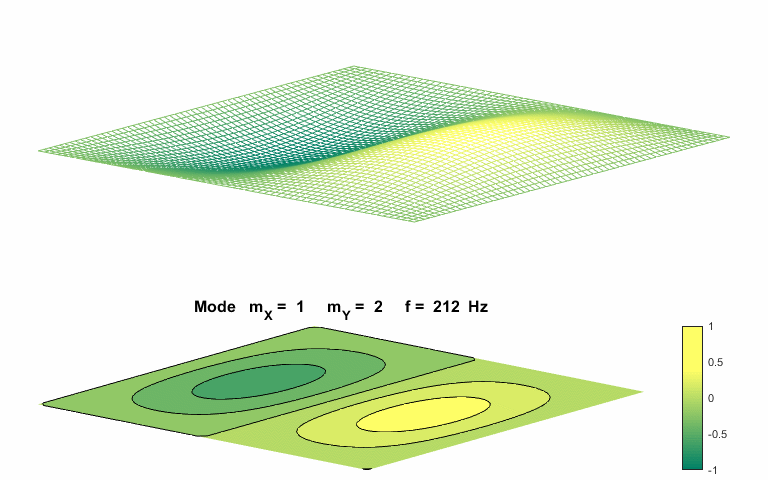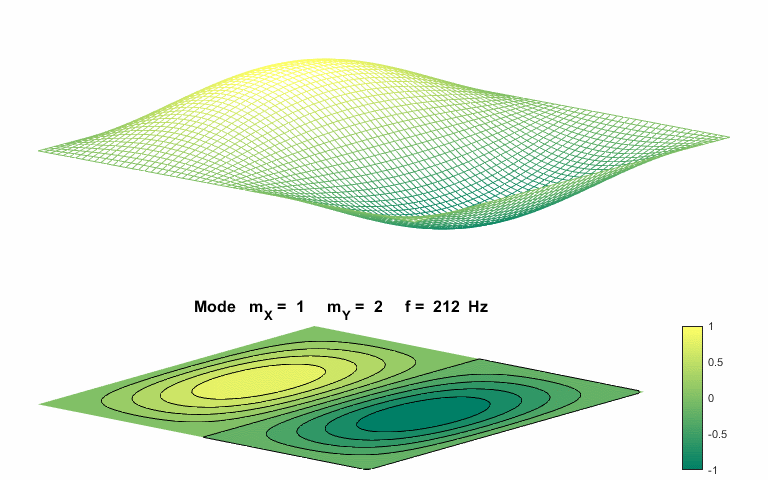
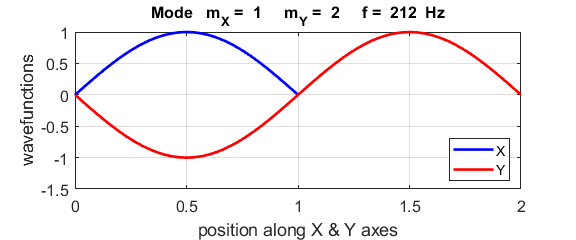
Normal mode of vibration   mX = 1    mY = 2

 

 

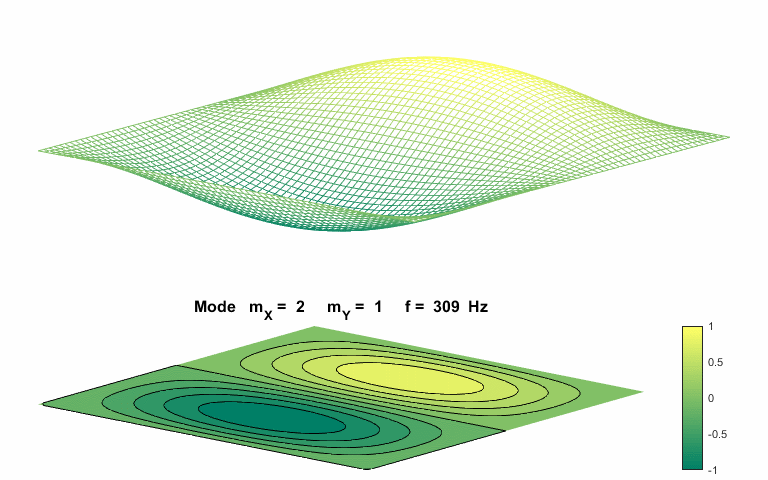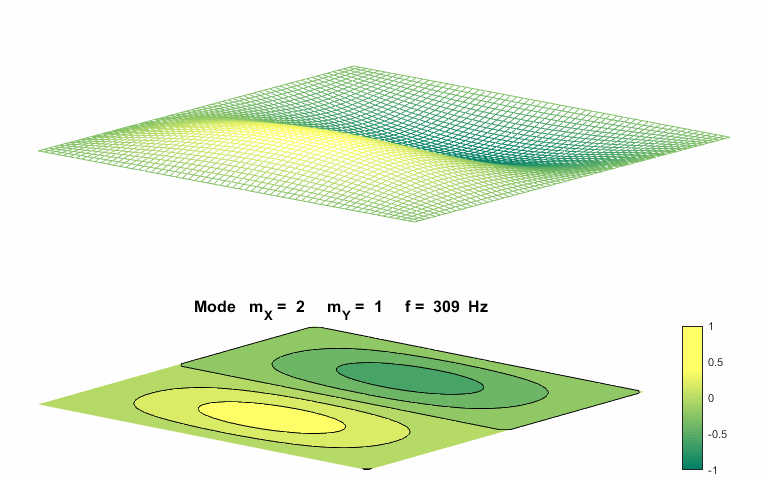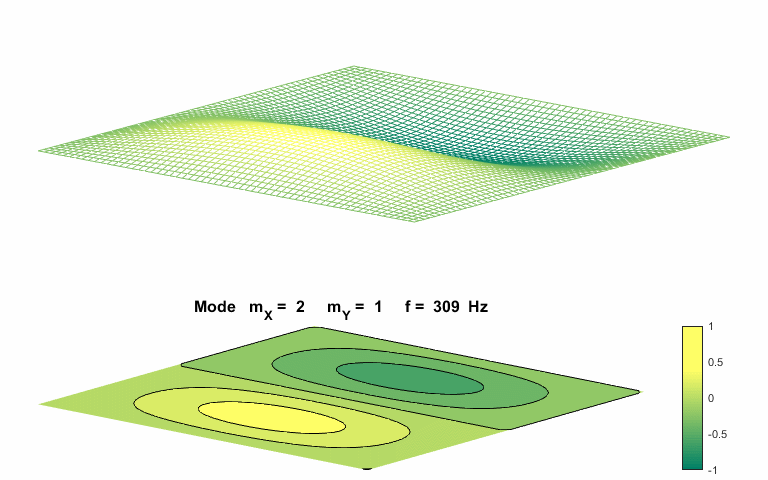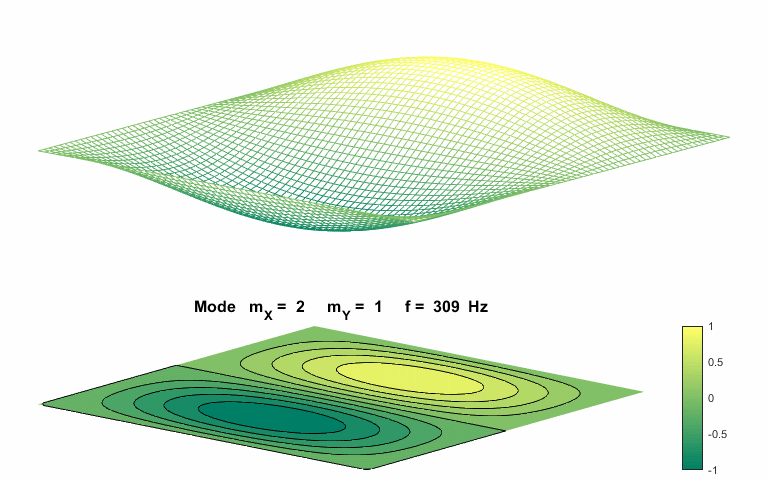
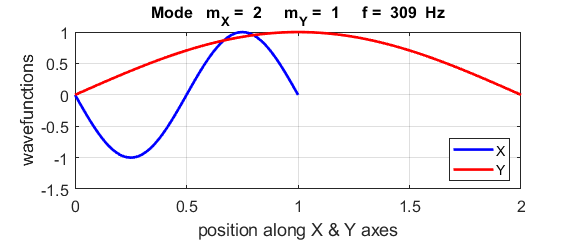
Normal mode of vibration    mX = 2    mY = 1

 

 

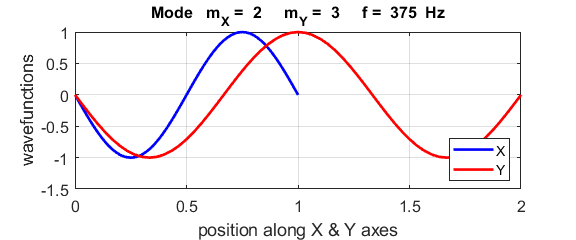
Normal mode of vibration   mX = 2    mY = 3

 

 

 

The natural frequencies of vibration for a rectangular membrane do not form a harmonic integer series. The patterns show nodal lines separating antinodal regions.

 

 

 

 

Ian Cooper

matlabvisualphysics@gmail.com