VISUAL PHYSICS ONLINE

2 KDYNAMICS

P20 020

Consider a smooth inclined plane which is a 3-4-5 triangle as shown in the figure. A 1.00 kg object is hung on the incline and connected to an object hanging vertically via the pully / string system.

What is the mass of the vertically hanging object for the System to be balanced? How can we figure this out? Think of two or even three different ways in which the problem can be solved.

View solution below only after you have completed answering the question. The solution is not in a form that you would answer in an examination. The answers are often in more detail to help improve your appreciation and understanding of the physics.

Solution

If the system is in balance, then the two objects are stationary or both move with a constant velocity with the same speed.

The problem can be solved using Newton’s Laws of Motion:

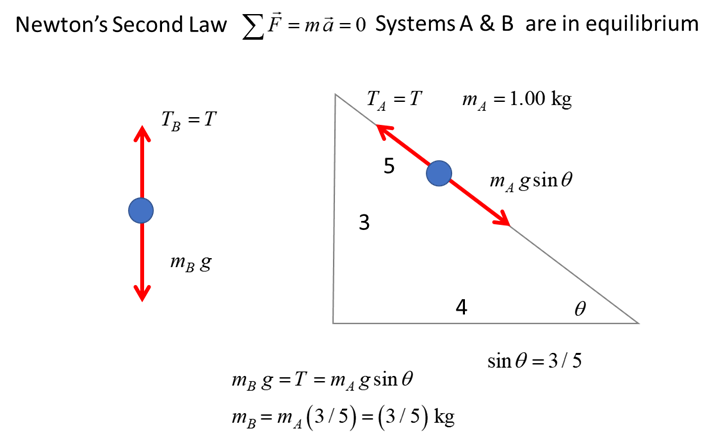
The problem can be solved using the principle of conservation of energy:

Gravitational potential energy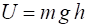

Assume that the object on the incline moves up a distance 5 m with a constant velocity, hence the vertically hanging mass must move vertically down a distance of 5 m with the same speed at any instant. The gain in gravitational potential energy by the object on the incline must be equal to the gravitation potential energy lost by the hanging object. So, the hanging object falls 5 m while the object on the incline must rise a distance of 3 m. Therefore, the mass of the hanging object is 3/5 times the mass of the object on the incline (3/5 kg).

More formally:

Gain in gravitational potential energy of system A

Loss in gravitational potential energy of system B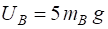

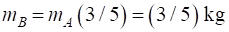
Stevinus found a brilliant or clever way to solve this problem. Did you think of it as well? His solution appears on his epitaph.

Simon Stevin (Dutch: 1548–1620), sometimes called Stevinus, was a Dutch-Flemish mathematician, physicist and military engineer. He was active in a great many areas of science and engineering, both theoretical and practical. He also translated various mathematical terms into Dutch, making it one of the few European languages in which the word for mathematics, wiskunde (wis and kunde, i.e., "the knowledge of what is certain"), was not a loanword from Greek but a calque via Latin.