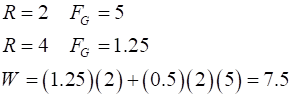|
VISUAL PHYSICS ONLINE 5
DYNAMICS P50 004.m The
gravitational force FG
as a function
of the distance R
between the
Earth and a spaceship was calculated in scaled units. When the distance of
the spaceship was R = 2.00 s.u.
from the centre of the Earth, the gravitational force was FG = 20.0 s.u. Plot a graph of
the gravitational force FG
as a function
of separation distance R
for the range R = 1 s.u. to R =1 0 s.u. For the
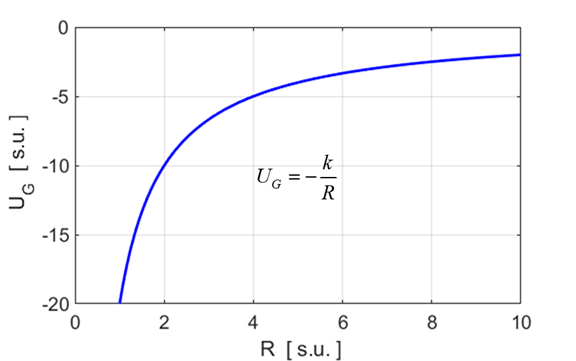
same range of separation distance, plot a graph of the gravitational
potential energy UG
of the Earth /
spaceship System against the separation distance R. Plot the
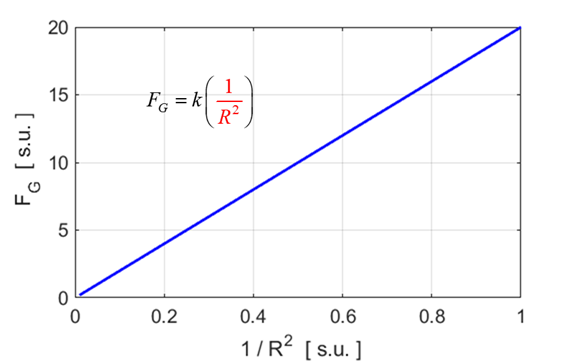
gravitational force FG
as some
function of separation distance R
such that the
graph is a straight line passing through the Origin. Plot the
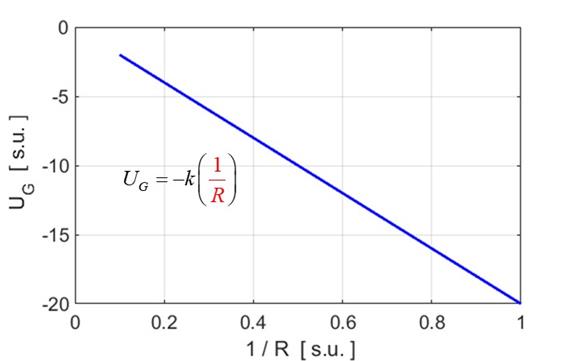
gravitational potential energy UG
as some
function of separation distance R
such that the
graph is a straight line passing through the Origin. Use the
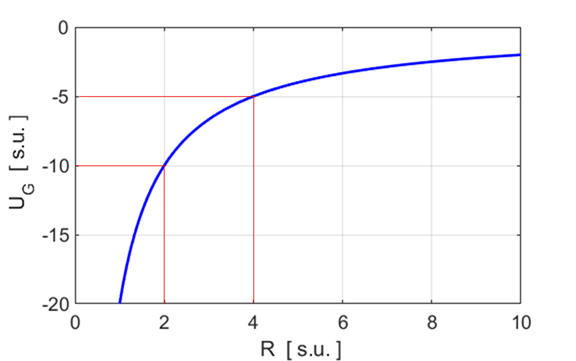
potential energy graphs to calculate the work required to move the spaceship
from R = 2 s.u. to R = 4 s.u. Use the
gravitation force graphs approximate a numerical value for work required to
move the spaceship from R = 2 s.u. to R = 4 s.u. View solution below only after you have completed the answering the question. |
|
Solution The gravitational force between the Earth and the spaceship is given by Newton’s Law of Universal Gravitation When R = 2, FG = 5, hence k = 20. The plot of FG against (1/R2) is a straight line through the Origin.
The gravitational potential energy of the Earth / spaceship System is given by the equation
The plot of UG against (1/R) is a straight line through the Origin.
The work W required for the
spaceship to move from R = 2 to R
= 4
The work done is given by the area under the force against displacement graph.
We can approximate the area under the force against displacement graph by finding the area of the rectangle plus triangle.
The answer is an over estimate and does not compare very well with the value of W = 5 estimated from the potential energy against displacement graph. |