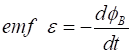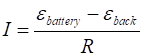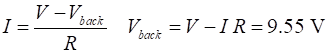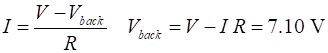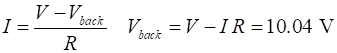VISUAL PHYSICS ONLINE

6 ELECTROMAGNETISM

P60 018

Motors and generators are very similar as they have the same construction (rotating coil in a magnetic field). Generators convert mechanical energy into electrical energy - when the coil is turned: the magnetic flux changes, and an emf is induced and for a complete circuit an induced current is generated. A motor converts electrical energy into mechanical energy – the coil carrying the current experiences a torque which is responsible for why the coil rotates. However, the motor acts as a generator whenever its coil rotates. Therefore, when the coil of the motor is rotating, an emf is generated. This self-generated emf is called the back emf. Lenz’s law tells us this back emf will oppose the change that created it, so that the battery emf that powers the motor will be opposed by back emf of the motor.

Faraday’s law of electromagnetic induction is

For a single coil of cross-sectional area A rotating in a uniform and constant magnetic field B, the induced emf is

Thus, the back emf is proportional to the motor’s angular speed (rotation speed) .

The motor’s current is

When the motor is first switched on, the coil has zero angular speed, and the back emf is zero, so the current through the motor is a maximum. As the motor turns faster and faster, the back emf increases, always opposing the battery emf, and reduces the voltage across the coil and the current it draws. Thus, when a motor first comes on, it draws more current than when it runs at its normal operating speed. When a mechanical load is placed on the motor, the back emf drops, more current flows, and more work can be done. If the motor runs at too low a speed, the larger current can overheat it due to ohmic heating , perhaps even burning it out. If there is zero mechanical load on the motor, the angular velocity will increase until the back emf is nearly equal to the driving emf and the motor will use only enough energy to overcome friction.

The single coil with cross-sectional area A in the magnetic field B of a simple DC motor with current I will experience a torque due to the magnetic force acting on a current element. The torque is given by

(A1)

You are moving the lawn will an electric lawn mower when the blades get struck on a tree root and stop rotating resulting in the mower no longer working. Explain why the lawn mower was damaged and could not be used again.

(A2)

Suppose you find that the belt drive connecting the motor to blades of the lawn mower is broken and the motor is left running freely. Should you be worried the motor is consuming a large amount of energy for no useful purpose? Explain.

Consider a simple DC motor that is used to lift a load as shown in the diagram.

(B)

Calculate the current when the motor was turned on and the maximum current drawn by the battery.

(C)

Calculate the torque required to lift the load at a constant speed.

What torque provided by the motor is required to lift the load at a constant speed?

(D)

When the load is being lifted at a constant speed, what is the coil current I ?

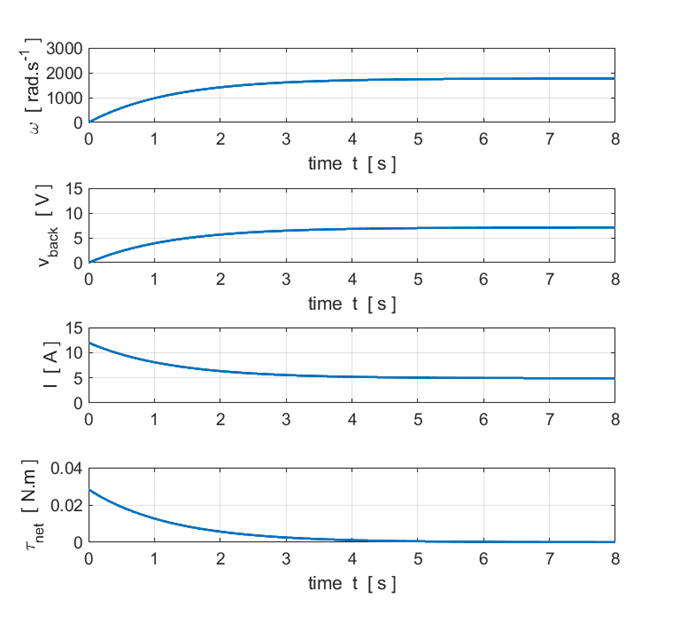
Calculate the back emf generated by the motor and the rotation speed of the motor.

(E)

Sketch four time graphs for angular speed of rotation of the motor, the back emf induced, the coil current and the net torque acting on the load from the time the motor was first turned on until it reached its operating speed where the load was being lifted at a constant speed.

(F)

If the mass of the load was doubled , how would the numerical values calculated above change (increase, decrease, stay the same)? How would the four graphs change?

Check your predictions by calculation all quantities.

(G)

If the mass of the load was reduced , how would the numerical values calculated above change (increase, decrease, stay the same)? How would the four graphs change?

Check your predictions by calculation all quantities.

(H)

Show that the principles of conservation energy can be applied to the System of the motor and load. Hence, show that energy is conserved by calculating the power associated with each energy transformation for different masses of the load , , and .

View solution below only after you have completed the answering the question.

Solution

(A1)

When the blades of the mower get stuck, the motor’s coil no longer turns in the magnetic field, therefore, zero emf is induced (). This results in a maximum current through the windings of the motor . The motor’s winding will heat up due to the Ohmic heating effect . This may result in damaging the windings to give an open circuit, so the mower no longer operates.

(A2)

When there is minimum load connected to a motor, it will spin with its maximum angular speed. Hence, the induced emf is a maximum and the current is nearly zero. So very little energy is supplied to the motor from the battery .

(B)

When the motor is switched on, the back emf is zero and maximum current is drawn from the battery

(C)

When the load is raised at a constant speed, the gravitational force exerted on the load must be equal in magnitude to the force (string tension) exerted on load by the string attached to the axle of the motor . The motor as it spins exerts the torque required to lift the load. The string attached to the axle of the motor of radius d exerts a force on the load through the string tension.

(D)

The maximum torque of the coil in the magnetic field of the motor is

The coil current and back emf are given by

The constant rotational speed of the motor is calculated from the back emf

(E)

(F)

The maximum torque of the coil in the magnetic field of the motor is

The coil current and back emf are given by

The constant rotational speed of the motor is calculated from the back emf

(G)

The maximum torque of the coil in the magnetic field of the motor is

The coil current and back emf are given by

The constant rotational speed of the motor is calculated from the back emf

(H)

Principle of conservation of energy energy supplied by battery equals the energy dissipated in the resistor plus the energy to operate the motor to lift the load. We are making a big assumption – we ignore all energy losses due to friction and other dissipative forces.

Power supplied by battery

Power dissipated by thermal energy in the resistor

Power utilized by motor in lifting load

In each case energy is conserved

Consider the case when and the time interval from t = 6.0 s to t = 7.0 s

The axle of the motor turns through an angle in this time interval

The length h of the string wound on the axle of the motor (radius of axis ) and hence the distance the load is raised is

The increase in potential energy of the load is

The rate at which the load potential energy increases is

Therefore,

the energy to lift the motor comes from the induced emf (back emf)

created by the rotation of the coil through the magnetic field of the motor.

The energy to operate the motor and lift the load comes from the induced emf as the conductor rotates in the magnetic field of the motor.

Summary of steady state values
mass m [kg]	0.08	0.10	0.20
[N.m]	0.0078	0.0098	0.0196
coil current I [A]	1.96	2.45	4.90
induced emf [V]	10.04	9.55	7.10
angular speed [rad.s^-1]	2.51x10³	2.39x10³	1.77x10³
P_battery [W]	23.54	29.43	58.86
P_resistor [W]	3.85	6.01	24.06
P_motor [W]	19.69	23.42	34.80
P_resistor + P_motor[W]	23.54	23.42	58.86
lifting load P_G [W]	19.69	23.42	34.80
Larger the load lower the rotation speed smaller the back emf greater the current greater energy dissipated by resistor why motors burn out if when motor spins slower than at its normal speed. Energy is conserved (assuming no energy losses due to friction or other dissipative forces other than through ohmic heating).