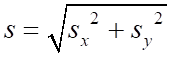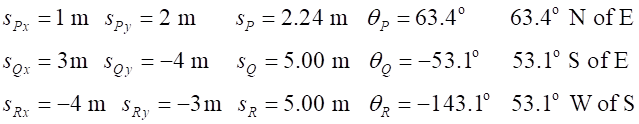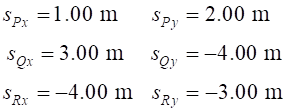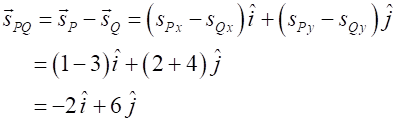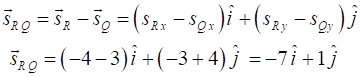FRAMES OF REFERENCE

Vectors / Unit Vectors

Ian Cooper

email matlabvisualphysics@gmail.com

What is the location of the tractor?

The answer depends upon the location of an observer. Position is a relative concept. The position of the tractor is different for the two observers.

Therefore, we need to set up a method of specifying the position of a System which is precise and unambiguous. We will consider a two-dimensional universe. The methods we will develop can easily be extended give the position of objects in our real three-dimensional world (in terms of modern physics, time and space are interwoven and a better model is to consider a four-dimensional world []).

To clearly specify the position of the tractor, we need to have a frame of reference. A frame of reference should include:

Observer

Origin O(0, 0, 0) reference point

Cartesian coordinate axes (X, Y, Z)

Unit vectors

Specify the units

Fig. 1A. Three examples of [2D] Cartesian coordinate System. We take any point in space as an Origin O. Through the origin O, we construct two lines at right angles to specify the X and Y coordinate axes. These lines could be labelled [X axis Y axis] or [N S E W] or [horizontal vertical].

The most useful frame of reference in three-dimensions is defined by three perpendicular lines and is referred to as a Cartesian Coordinate System (figure 1).

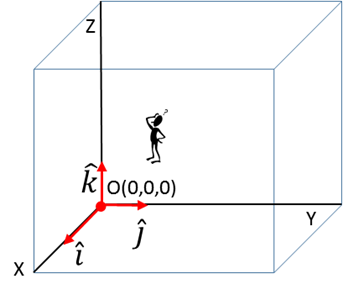
Fig. 1B. Cartesian coordinate System with X, Y and Z axes each perpendicular to each other. The direction of the Z axis is given by the direction of the thumb of the right hand when the fingers of the right hand are rotated from the X axis to Y axis.

The unit vectors , , give the directions along the Cartesian coordinate axes and allows us to specify a vector and its Cartesian components in a convenient format. The magnitude of a unit vector is 1.

· gives the direction that the X coordinate is increasing (say i-hat)

· gives the direction that the Y coordinate is increasing (j-hat)

· gives the direction that the Z coordinate is increasing (k-hat)

The concept of unit vectors is not usually used at the high school level but using the notation of unit vectors in the “long run” improves your ability to have a better understanding of physical principles and actually makes the physics simpler.

Consider the problem of specifiying the position (location) of three cars as shown in figure 2.

Fig. 2. What is the position of the three cars?

Figure 3 gives the position of the cars in our frame of reference where the objects – the cars are replaced by dots.

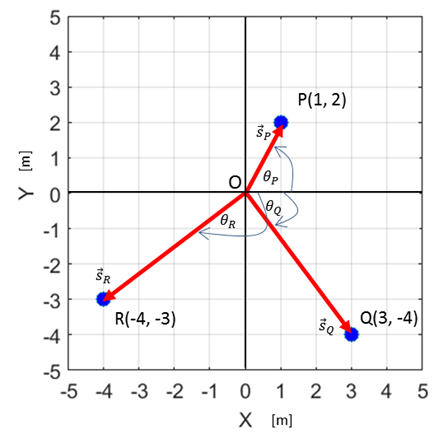
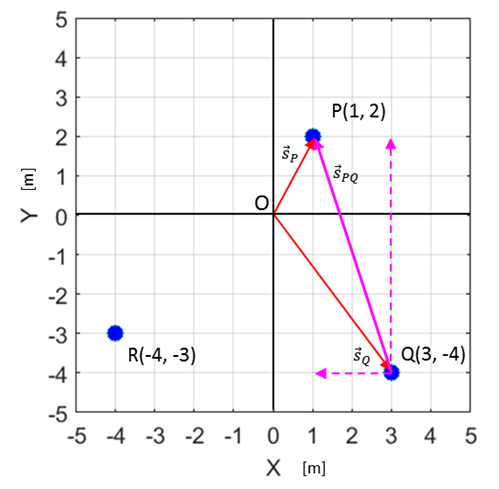
Fig. 3. The location of the cars in our Cartesian coordinate system with origin O(0,0).

The location of the cars with respect to the Origin O is uniquely given in terms of their X and Y coordinates. We can identify the three cars using the labels: P(red car), Q(yellow car) and R(grey car).

Location of the cars in our frame of reference (X coordinate, Y coordinate)

Red car P(1, 2)

Yellow car Q(3, -4)

Grey car R(-4, -3)

The best way to specify the location of the cars is in terms of the vector quantity called the displacement which is specified by its X and Y coordinates which corresponds to the X and Y components of the vector with respect to the Origin (0, 0) and the unit vectors and

The magnitude of the displacement vector for a car is the straight line distance between the Origin O and the location of the car. The direction is given by the angle measured with respect to the X axis (figure 4).

Fig. 4. The displacements of the car with respect to the origin O.

The distance s between the origin O(0,0) and a point at is given by equation 1 and is called the magnitude of the vector

(1) Pythagoras’ Theorem

The magnitude of a vector is always zero or a positive scalar quantity.

The direction of a point at makes with the X axis is be given by the angle (Greek letter theta) as expressed by equation 2

(2)

The components and displacement vectors of the three cars using equations 1 and 2 are:

The subscript P (red car), Q(yellow car) and R(grey) are used to identify the cars.

The displacement of the cars can be expressed in terms of the unit vectors and X and Y components of the vector

For car P (red car)

For car Q (yellow car)

For car R (grey car)

All the calculations of the displacements were measured with respect to our observed located at the origin O(0, 0).

RELATIVE POSITIONS

We can also calculate relative positions. For example, what are the displacement of the cars with respect to an observed located at the position of car Q. The calculation of relative positions can be done using the concept of vector subtraction.

The vector components of the three cars are:

The position of car Q with respect to the observer at Q is given by the vector

where the first subscript is the object and the second subscript is the observed. Obviously, the answer is correct: the displacement of the car at Q w.r.t the observer at Q is zero.

The position of car P with respect to the observer at Q as shown in figure 5 is given by the vector

where the first subscript is the object P and the second subscript Q is the observed at Q.

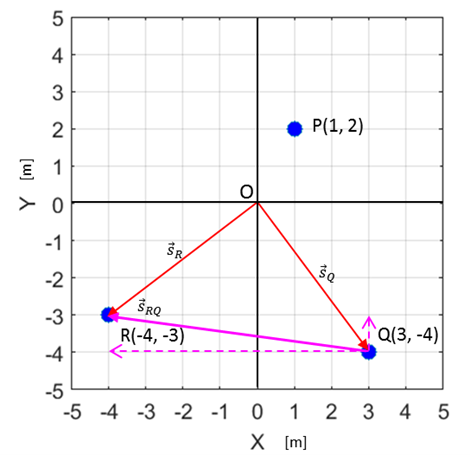
Fig. 5. The position of car P w.r.t. an observed located at Q.

The position of car R with respect to the observer at Q as shown in figure 6 is given by the vector

where the first subscript is the object R and the second subscript Q is the observed at Q.

Fig. 6. The position of car R w.r.t. an observed located at Q.

REVIEW

In specifying a vector quantity, it is necessary to have defined a frame of reference (Cartesian coordinate system and origin - observer).

For [2D] vectors, the vector has a magnitude s or and a direction and components

Vector

Magnitude is a positive scalar quantity

Direction (w.r.t X-axis)

Components

Fig. 7. Specifying a [2D] vector quantity.

· A vector has a magnitude and direction. You can’t associate a positive or negative number to a vector. Only the components of a vector are zero or positive or negative numbers.

· Scalars are not vectors and vectors are not scalars.

· In answering most questions on kinematics and dynamics you should draw an annotated diagram of the physical situation. Your diagram should show objects as dots; the Cartesian coordinate system; the origin and observer; the values of given and implied physical quantities; a list unknown physical quantities physical; the units for all physical quantities; principles and equations.