VISUAL PHYSICS ONLINE

THE LANGUAGE OF PHYSICS

SCALAR AND VECTORS

Ian Cooper

email matlabvisualphysics@gmail.com

SCALAR QUANTITIES

Physical quantities that require only a number and a unit for their complete specification are known as scalar quantities.

mass of Pat m_Pat = 75.2 kg

Pat’s temperature T_Pat = 37.4 ^oC

Pat’s height h_Pat = 1555 mm

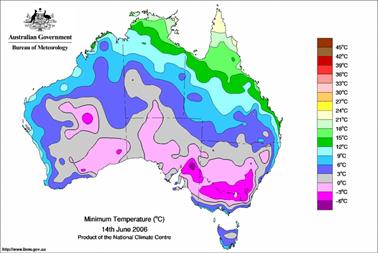
Fig. 1. Scalar temperature field. At each location, the temperature is specified by a number in ^oC.

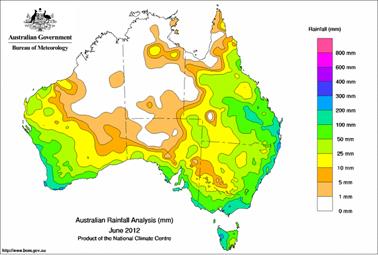
Fig. 2. Scalar rainfall field. At each location, the rainfall is specified by a number in mm.

In physics, a scalar field is a region in space such that each point in the space a number can be assigned. Examples of scalar fields are shown in figures 1 and 2 for temperature and rainfall distributions in Australia respectively.

VECTORS

magnitude direction components

Physical quantities that require for their complete specification a positive scalar quantity (magnitude) and a direction are called vector quantities.

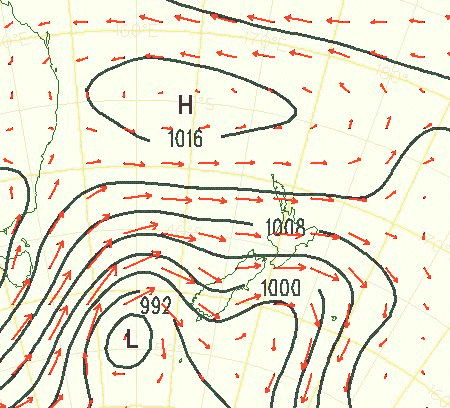
Today the wind at Sydney airport is

Fig. 3. A magnitude and direction is needed to specify the wind. The black lines represent the pressure (scalar) and the red arrows the wind (vector). The length of an arrows is proportional to the magnitude of the wind and the direction of the arrow gives the wind direction.

A vector quantity can be visualized as a straight arrow. The length of the arrow being proportional to the magnitude and the direction of the arrow gives the direction of the vector.

A vector quantity is written as a bold symbol or a small arrow above the symbol. Often a curved line draw under the symbol is used when the vector is hand written.

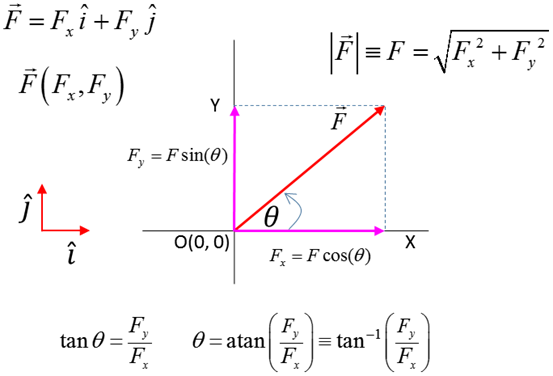
The [2D] vector is specified in a frame of reference using an XY Cartesian coordinate by its

Magnitude (size) positive scalar quantity

Direction measured w.r.t. X axis

X component projection of vector onto X axis

Y component projection of vector onto Y axis

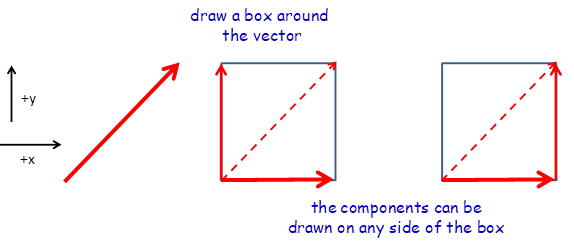
Resolving a vector into its components

A vector quantity can be resolved into components along each of the coordinate axes. To find the components of a vector draw a box around the vector and then draw the two Cartesian components as shown in figure (7).

Fig. 4. Resolving a vector into its X and Y components.

N.B. The two Cartesian components replace the original vector. Avoid the mistake of many students who add the two components to the original vector, thus counting it twice.

Vector algebra

· Two vectors are equal if they have the same magnitude and small direction .

· The negative of any vector is a vector of the same magnitude and opposite in direction. The vectors and are antiparallel.

· Multiplication of a vector by a scalar . The new vector has the same direction and a magnitude .

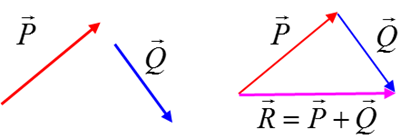
· Vector addition: vectors can be added using a scaled diagram where the vectors are added in a tail-to-head method or by adding the components. The sum of the vectors is called the resultant vector.

The vector is the resultant vector.

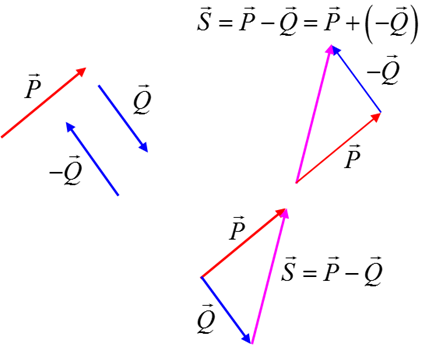
· Vector subtraction: can be found by using the rule of vector addition

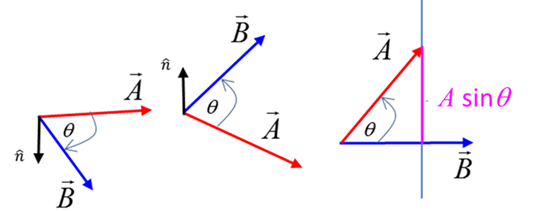
· Two vectors can’t be multiplied together like two scalar quantities. Only vectors of the same physical type can be added or subtracted. But vectors of different types can be combined through scalar multiplication (dot product) and vector multiplication (cross product).

· Scalar product or dot product of the vectors and is defined as

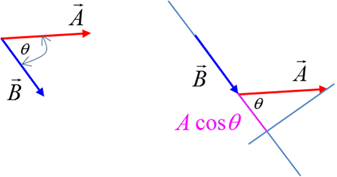
The projection or component of on the line containing is . The angle between the two vectors is always a positive quantity and is always less than or equal to 180^o. Thus, the scalar product can be either positive, negative or zero, depending on the angle between the two vectors .

The result of the scalar product is a scalar quantity. If two vectors are perpendicular to each other, then the scalar product is zero . This is a wonderful test to see if two vectors are perpendicular to each other.

If the two vectors are in the same direction, then the scalar product is A B .

· The vector product or cross product of two vectors and is defined as

The magnitude of the vector is .

The vector is a unit vector which is perpendicular to both the vectors and .

The angle between the two vectors is always less than or equal to 180^o. The sine over this range of angles is never negative, hence the magnitude of the vector product is always positive or zero .

The direction of the vector product is perpendicular to both the vectors and . The direction is given by the right-hand screw rule. The thumb of the right hand gives the direction of the vector product as the fingers of the right hand rotate from along the direction of the vector towards the direction of the vector.

VECTOR EQUATIONS

Consider the motion of an object moving in a plane with a uniform acceleration in the time interval t. The physical quantities describing the motion are

Time interval [s]

Displacement [m]

Initial velocity [m.s^-1]

Final velocity [m.s^-1]

Acceleration [m.s^-2]

The equation describing the velocity as a function of time involves the vector addition of two vectors

The equation describing the displacement as a function of time involves the vector addition of two vectors

The velocity as a function of displacement.

Warning: the equation stated in the syllabus is totally incorrect

this equation is absolute nonsense

Two vectors can’t be multiplied together. The correct equation has to show the scalar product between two vectors

This equation should not be given in vector form but expressed as two separate equations, one for the X components and one for the Y components

Work and the scalar product

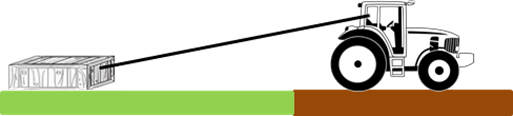
Consider a tractor pulling a crate across a surface as shown in figure 5.

Fig. 5. A crate being pulled by a tractor.

We want to setup a simple model to consider the energy transferred to the crate by the tractor. In physics, to model a physical situation, one introduces a few simplifications and approximations. So, we will assume that the crate is pulled along a frictionless surface by a constant force acting along the rope joining the tractor and crate. We then draw an annotated scientific diagram of the situation showing our frame of reference.

The crate becomes the System for our investigation and the System is drawn as a dot and the forces acting on the System are given by arrows as shown in figure 5.

Fig. 6. The System is the cart (brown dot). The forces acting on the System are the force of gravity , the normal force and the tension of the rope .

Energy is transferred to the System by the action of the forces doing work on the System. Work is often said to be equal to a force multiplied by a distance . This is a poor definition of work.

A much better definition of the work done by a constant force causing an object to move along a straight line is to use the idea of scalar (dot) product

work is a scalar quantity

where the angle is the angle between the two vectors and . The angle between the two vectors is always a positive quantity and is always less than or equal to 180^o hence . Work is a scalar quantity. However, its numerical value can be zero, positive or negative. If W > 0, work is done on the object and if W < 0, then work is done by the object.

Work done by the gravitational force and by the normal force are zero because the angle between the force vectors and displacement vector is 90^o (cos(90^o) = 0).

The work done by the tension force is

Hence, the work done on the System is the component of the force parallel to the displacement vector multiplied by the magnitude of the displacement.

Torque and the vector product

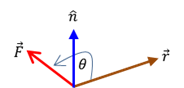
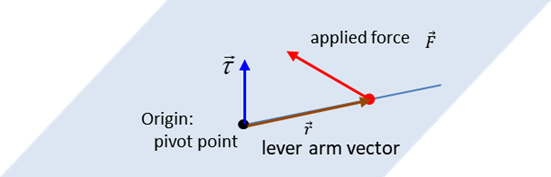
What is the physics of opening a door?

It is the torque applied to the door that is important and not the force.

A force can cause an object to move and a torque can cause an object to rotate. A torque is often thought of as a force multiplied by a distance. However, using the idea of the vector (cross) product we can precisely define what we mean by the concept of torque.

The vector is the torque applied, the vector is the lever arm distance from the pivot point to the point of application of the force . The angle is the angle between the vectors and . The direction of the torque is found by applying the right-hand screw rule: the thumb points in the direction of the torque as you rotate the fingers of the right hand from along the line of the vector to the vector . The torque is perpendicular to both the position vector and the force .

The concept of the scalar product is not often used at the high school level, but, by being familiar with the concept of the scalar product you will have a much better understanding of the physics associated with motion.

Also, the concepts of unit vectors, scalar product and vector product are not covered in the Syllabus. However, having a more in-depth knowledge will help you in having a better understanding of Physics and will lead to a better performance in your examinations.

· A vector has a magnitude and direction. You can’t associate a positive or negative number to a vector. Only the components of a vector are zero or positive or negative numbers.

· Scalars are not vectors and vectors are not scalars.

· In answering most questions on kinematics and dynamics you should draw an annotated diagram of the physical situation. Your diagram should show objects as dots; the Cartesian coordinate System, the Origin and observer; the values of given and implied physical quantities; a list unknown physical quantities physical; the units for all physical quantities; principles and equations.