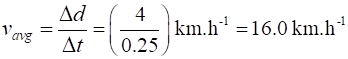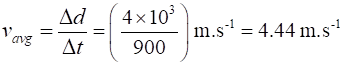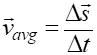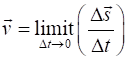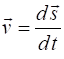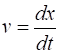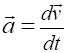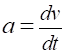VISUAL PHYSICS ONLINE

RECTILINEAR MOTION:

DISPLACEMENT

VELOCITY

ACCELERATION

Ian Cooper

email matlabvisualphysics@gmail.com

DISTANCE AND DISPLACEMENT

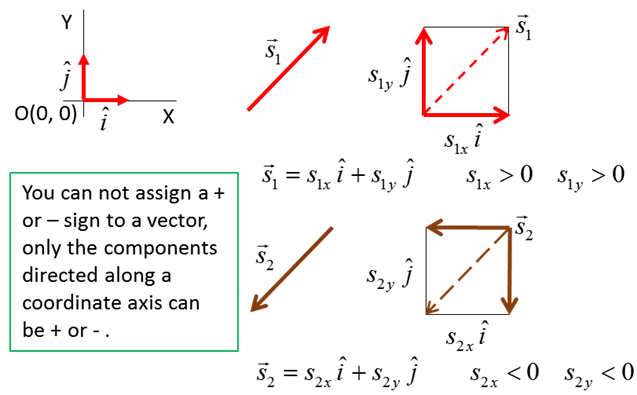
In this document on kinematics will we only consider the motion of objects in one-dimension. This is called rectilinear motion. Previously, we looked at the motion of a particle in a plane [2D] where the motion was expressed in terms of the components directed along the Cartesian coordinate axes. One advantage of studying [1D] motion is that we don’t have to use vector notation for displacement, velocity and acceleration even though they are vectors. You can’t associate a positive or negative sign with a vector quantity, however, the components of the vector are negative or zero or positive. Consider the displacement vectors shown in figure (1).

Fig. 1. A vector can’t be a positive or negative number but its components can be negative or zero or positive.

Before reading further, view the animation of the rectilinear motion of a tram that travels to the right then back to the left. Think about the scientific language that you will need to describe the motion of the tram

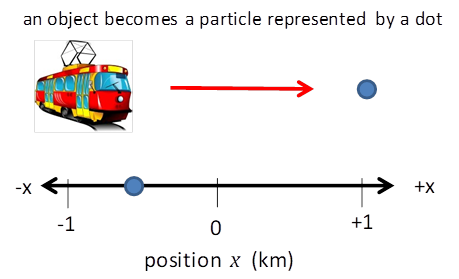
To describe the motion of a moving object you must first define a frame of reference (Origin and X axis) and the object is represented as a point particle.

Consider the tram moving backward and forwards along a straight 2.00 km track. The X axis is taken along the track with the Origin at x = 0. The left end of the track is at x = -1.00 km and the right end of the track is at x = +1.00 km. The tram start at time at the left end of the track and moves to the right where it stops at the right end and returns to the left end of the track arriving at a later time . At any time , the position of the tram is given by its X coordinate as shown in figure (2).

Fig. 2. A frame of reference for the rectilinear motion of the tram with the Origin at x = 0. The trams travels from the left to the right end and travels back to the left end of the track.

Event #1: At time the tram starts its journey at position km.

Event #2: At time hours the train completes one cycle to the right end of the track and back again where the final position of the train is km.

The time interval for the journey is

is the Greek letter Delta meaning change in or increment.

is one symbol

N.B. Time and time interval are different physical quantities.

The distance travelled is

The magnitude of the displacement is the straight line distance between the initial position and the final position

Distance travelled (scalar) is not the same physical quantity as displacement (vector)

SPEED AND VELOCITY

Speed and velocity refer to how fast something is travelling but are different physical quantities. Also, we need to distinguish between average and instantaneous quantities.

The average speed of a particle during a time interval in which the distance travelled is defined by equation (1)

(1) definition of average speed

The average speed is a positive scalar quantity and not a vector.

The average velocity of a particle is defined as the ratio of the change in position vector of the particle to the time interval during which the change occurred as given by equation (2)

(2) definition of average velocity

For one-dimensional motion directed along the X axis we do not need the use the vector notation shown by the arrow above the symbol.

In the example of our tram:

average speed

S.I. units

average velocity

N.B. very different values for the average speed and average velocity. Often the same symbol is used for speed and velocity. You always need to state whether the symbol represents the speed or velocity.

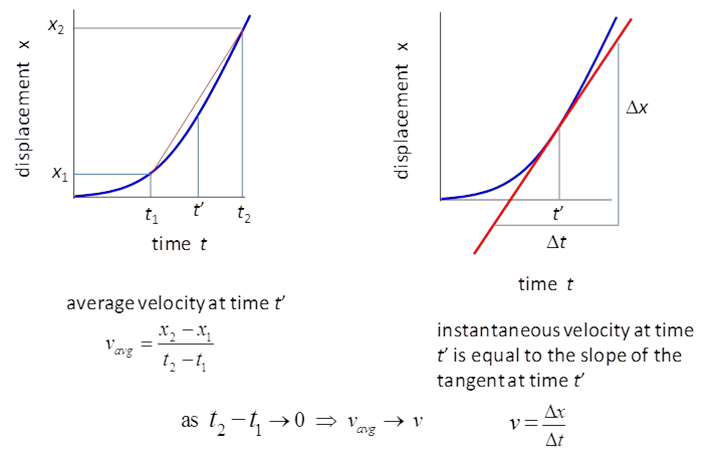
Our tram speeds up continually until it reaches the Origin, it then slows down and stops at the right end of the track. In the return journey, it continually speeds up until it reaches the Origin it then slows down and stops at the left end of the track. The speed and velocity are always changing. Hence, it is more useful to talk around instantaneous values rather than average values. The instantaneous velocity is a vector quantity whose magnitude is equal to the instantaneous speed and who instantaneous direction is in the same sense to that in which the particle is moving at that instant. The velocity vector is always tangential to the trajectory of the particle at that instant. Remember, speed and velocity are not the same physical quantity even though they have the same S.I. unit [m.s^-1].

The average velocity given by equation (3) is

(3)

If we make the time interval smaller and smaller, the average velocity approaches the instantaneous value at that instant. Mathematically it is written as

This limit is one way of defining the derivative of a function. The instantaneous velocity is the time rate of change of the displacement

(4) definition of instantaneous velocity

For rectilinear motion along the X axis, we don’t need the vector notation and we can simply write the instantaneous velocity as

(5) rectilinear motion

You don’t need to know how to different a function, but you have to be familiar with the notation for differentiation and be able to interpret the process of differentiation as finding the slope of the tangent to the displacement vs time graph at one instant of time as shown in figure (3).

Fig. 3. The average and instantaneous velocities can be found from a displacement vs time graph. The slope of the tangent gives the instantaneous velocity (derivative of a function).

As the time interval approaches zero , the distance travelled approaches the value for the magnitude of the displacement . Therefore, the magnitude of the instantaneous velocity is equal to the value of the instantaneous speed. This is not the case when referring to average values for the speed and velocity.

When you refer to the speed or velocity it means you are talking about the instantaneous values. Therefore, on most occasions you can omit the word instantaneous, but you can’t omit the term average when talking about average speed or average velocity.

ACCELERATION

Velocity is related to how fast an object is travelling. Acceleration refers to changes in velocity. Since velocity is a vector quantity, an acceleration occurs when

· an object speeds up (magnitude of velocity increases)

· an object slows down (magnitude of velocity decreases)

· an object changes direction (direction of velocity changes)

Acceleration is a vector quantity. You don’t sense how fast you are travelling in a car, but you do notice changes in speed and direction of the car especially if the changes occur rapidly – you “feel” the effects of the acceleration. Some of the effects of acceleration we are familiar with include: the experience of sinking into the seat as a plane accelerates down the runway, the "flutter" in our stomach when a lift suddenly speeds up or slows down and “being thrown side-ways” in a car going around a corner too quickly.

The average acceleration of an object is defined in terms of the change in velocity and the interval for the change

(6) definition of average velocity

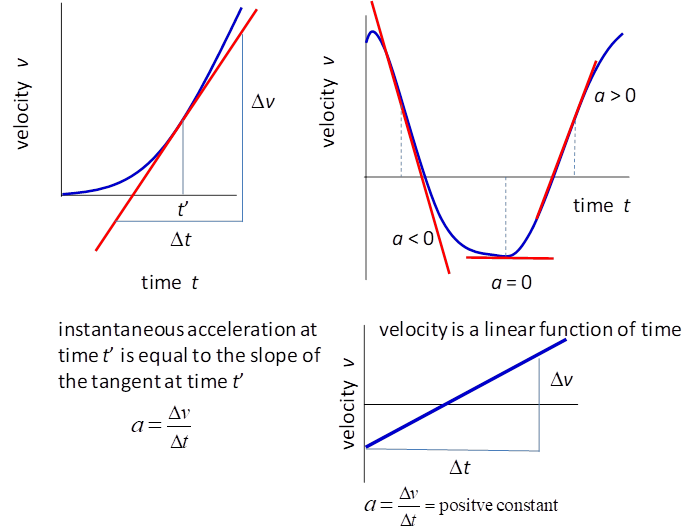
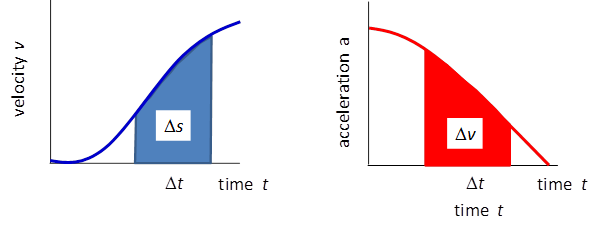
The instantaneous acceleration (acceleration) is the time rate of change of the velocity, i.e., the derivative of the velocity gives the acceleration (equation 6). Again, you don’t need to differentiate a function but you need to know the notation and interpret it graphically as the acceleration is the slope of the tangent to a velocity vs time graph as shown in figure (4). The area under the acceleration vs time graph in the time interval is equal to the change in velocity in that time interval as shown in figure (5).

(7) definition of instantaneous acceleration

(8) rectilinear motion

Fig. 4. Velocity vs time graphs for rectilinear motion. The slope of the tangent is equal to the acceleration. For the special case when the velocity is a linear function of time (straight line) the acceleration is constant.

The reverse process to differentiation is integration. Graphically, integration is a process of finding the area under a curve.

The slope of the tangent to the displacement vs time graph is equal to the velocity.

The area under a velocity vs time graph in a time interval is equal to the change in displacement in that time interval.

The area under a acceleration vs time graph in a time interval is equal to the change in velocity in that time interval.

Fig. 5. The area under the velocity vs time graph in the time interval is equal to the change in displacement in that time interval. The area under the acceleration vs time graph in the time interval is equal to the change in velocity in that time interval.