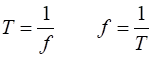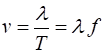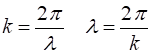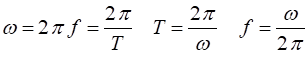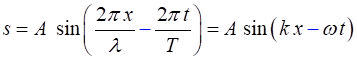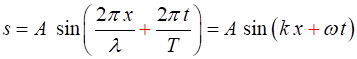|
WAVES THE LANGUAGE DESCRIBING
WAVE MOTION
WAVE MOTION Most information
about our surroundings arrives as a wave: sounds are transpoted to our ears;
light to our eyes and electromagnetic radiaiton to our mobile phones. Through
wave motion, energy can be transferred from a source to a receiver without
the transfer of matter between the two points. A good visual example
are the waves on the surface of water. When a stone is dropped into a lake,
waves will be generate that travel outwards in expanding circles, with the
centres as the source of the disturbance. The wave propagates, not the water.
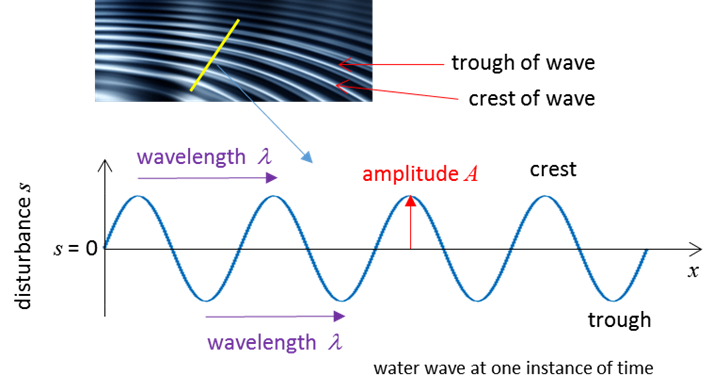
Fig.1. Snap shot of the waves on the surface of
water. At each point, the water bobs up an
down. The shape of the wave can be approximated by a sine curve. |
|
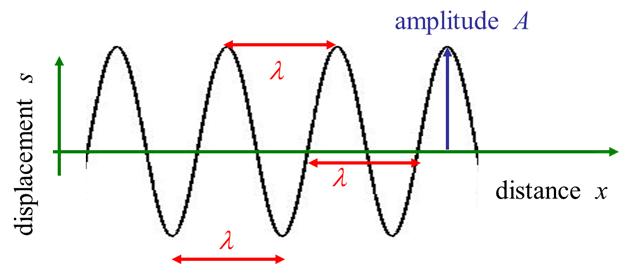
DESCRIBING WAVES Consider a simple model for the
propagation of a wave along the X axis which is represented pictorially as a sine function that depends both on time The amplitude The wavelength The frequency 1
kHz = 103 Hz (kilo) 1 MHz = 106 Hz (mega) 1GHz = 109 Hz (giga) The period (1)
AM radio waves are broadcast in the
kHz range FM radio waves are broadcast with
MHz frequencies Microwaves have GHz frequencies
Audible sounds are
generally in the range from ~ 1 Hz to < 20 kHz The energy carried by a wave is
approximately proportional to the square of the wave frequency. The higher
the frequency the higher the transfer of energy in a given
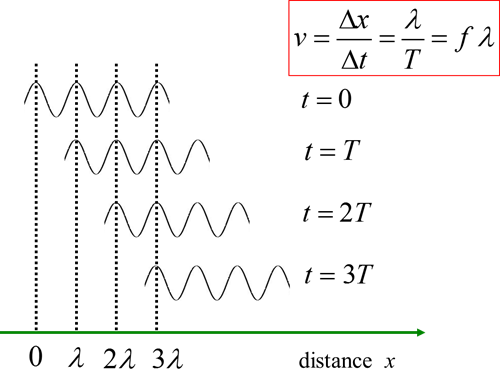
time interval. The speed
(2) This relationship holds
true for all types of waves, whether they are water waves, sound waves, waves
on strings or electromagnetic waves. It is mathematically very convenient
to define two other quantities in describing waves: the wave number or propagation constant
(3) (4) The shape of a sinusoidal wave is
given by
(5a) wave travelling to the right (+ X direction)
(5b)
wave travelling to the
left (- X direction) The symbol
The term Equations 5a and 5b describe a travelling sinusoidal wave (harmonic wave). Because the wave function depends both on time and position, it is impossible to draw a simple graph of the wave function. The function must be animated or shown as a graph at a fixed time or a graph showing the variation with time at a fixed location. |
|
|
|
|
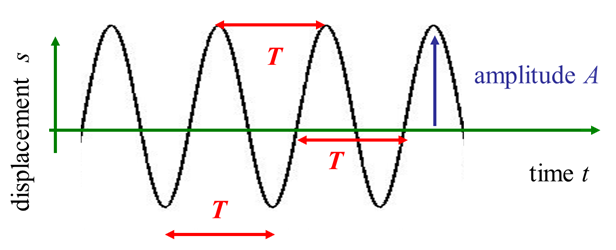
Fig. 2a. A harmonic wave: at any
position is a sinusoidal function of time |
|
Fig. 2b. A harmonic wave: at any time is a sinusoidal function of position |
|
Fig. 3. Wave or propagation
velocity (phase velocity) |
|
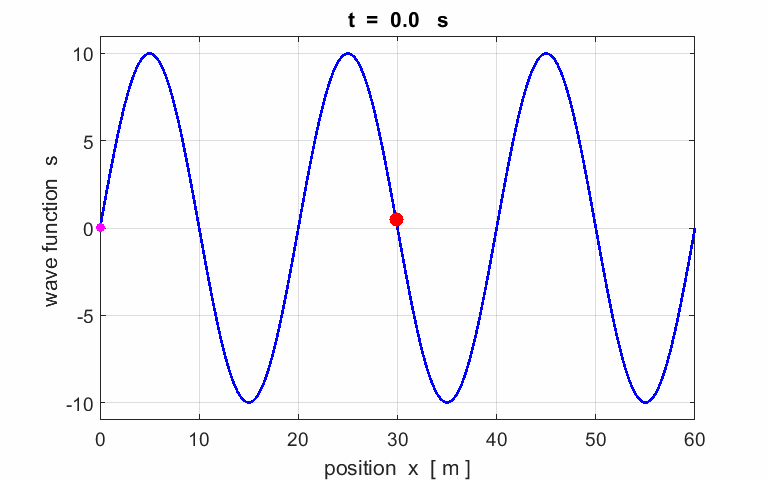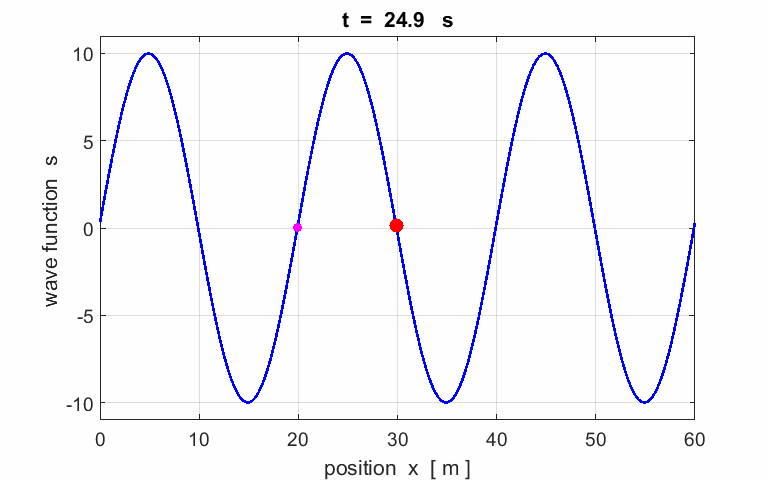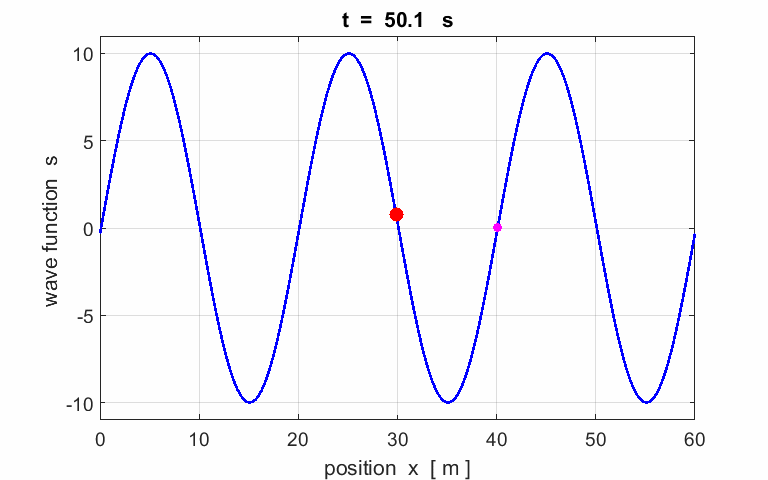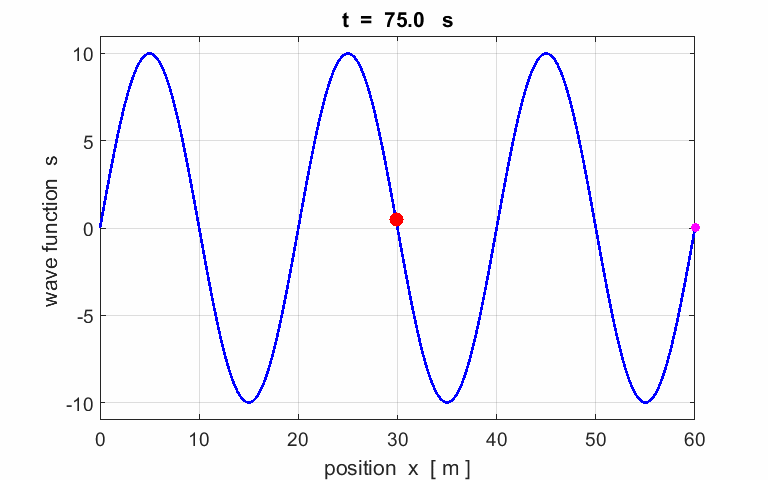
Exercise 1
Calculate the following parameters from the
animation of a travelling wave:
amplitude wavelength period phase velocity
frequency angular
velocity wave number Describe the motion of the particle (red) located at |
|
Animation
produced with wm_travelling.m If you have any feedback, comments, suggestions or corrections please email: Ian Cooper
School of Physics University
of Sydney ian.cooper@sydney.edu.au |