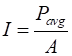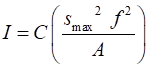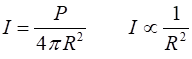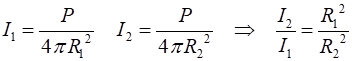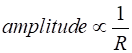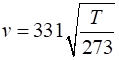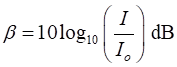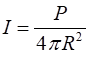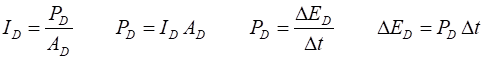|
WAVES BEHAVIOUR OF WAVES ENERGY TRANSPORTED
BY WAVES Waves
transport energy from one place to another.
To a good approximation, the energy transported by a wave is
proportional to its square of the amplitude The intensity If a wave spreads out
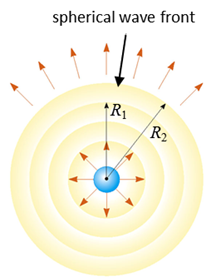
form the source in all directions, it is a three-dimensional wave. If the
energy spreads uniformly in all directions in a isotropic medium (same in all
directions), the wave is said to be a spherical wave. As the wave moves
outward, the energy it carries is spread over a larger and larger area since
the surface area of a sphere of radius This is known as the inverse square law.
|
|
If we consider two
points at distances For example, if the distance doubles, then
the intensity is reduced by a
|
|
|
The amplitude of a wave also decreases with
distance. Since the intensity is proportional to the square of the amplitude,
then the amplitude must be inversely proportional to the distance
When a wave is twice as far from its
source, the amplitude is half as large (spherical wave propagating in an
isotropic medium). A wavefront is a line or surface that joins
points of same phase. For water waves travelling on the surface
from a point source, the wavefronts are circles. For sound waves emanating
from a point source, the wavefronts are spherical surfaces. In modelling
waves propagating in one-dimension, the waves are referred to as plane waves.
|
|
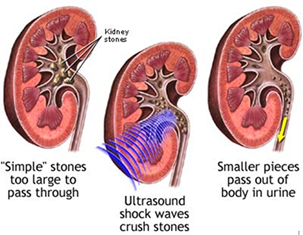
SPEED
OF SOUND The speed of sound is different in
different materials and is very dependent on the temperature for gaseous
media. The more elastic the medium the greater the speed and the greater the
density the slower the speed. The speed of sound in air at a temperature The
dependence of the speed of sound on the air temperature leads to interesting
effects on the propagation of sound due to refraction (bending of the
wavefronts due to change in speed of the wave). |
|
SOUNDS and HEARING Sounds are the longitudinal waves due to
the vibrations of molecules. In air, the sound that we perceive is associated
with our sense of hearing and, therefore, with the physiology of our ears and
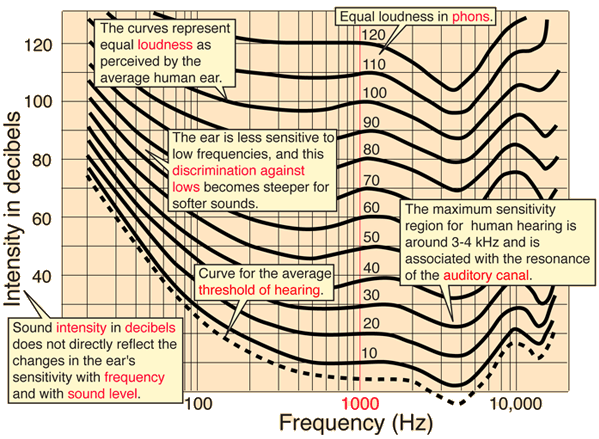
the psychology of our brain. Two aspects of any sound are its loudness
and pitch.
Loudness and pitch are subjective quantities and depend upon the
consciousness of the listener.
Loudness
is related to the energy in the sound wave and its frequency.
Pitch
is related to frequency and changes in energy and refers to whether the sound
is high (violin) or low (bass drum). The higher the frequency the higher the
pitch. The human ear responds to the audible range of frequencies from about 20 Hz to less than 20 kHz. As we get older, we lose the ability to hear the higher frequency components of any sound. Some people with hearing problems can only hear frequencies less than about 8 kHz. |
|
One resonance (natural) frequency of the auditory canal is around 3000 Hz, so, sounds with component frequency near 3000 Hz are perceived to be loud than other sounds. |
|
Sounds
are longitudinal wave that can propagate through any medium which can be
compressed such as a gas, liquid or solid. In air, audible human hearing frequency range is ~20 Hz to ~ 20
kHz. Frequencies less than 20 Hz are called infrasound.
Animals have been known to perceive the infrasonic waves going through the
Earth caused by natural disasters and can use these as an early warning. A
recent example of this is the 2004 Indian Ocean earthquake and tsunami.
Animals were reported to flee the area hours before the actual tsunami hit
the shores of Asia. Infrasound is one of several techniques used to identify
if a nuclear detonation has occurred. Frequencies
above 20 kHz are called ultrasound. Many animals can hear ultrasound
frequencies: dogs hear sounds as high as 50 kHz and but can detect frequency
as high as 100 kHz. Small
objects can be imaged using ultrasonic waves because of their short
wavelengths (high frequencies). So, ultrasound waves are used widely in
medicine to image internal organs and blood vessels. The images are produced
by the reflection and absorption of ultrasonic waves. Use of ultrasonic waves
is safer than X-rays but the images show less details. Certain organs such as
the liver and the spleen are invisible to X-rays but visible to ultrasonic
waves. |
|
|
Blood flow through the placenta
using utrasonic waves. Applying the principle of the
Doppler Effect, the speed of blood flow can be estimated. |
|
|
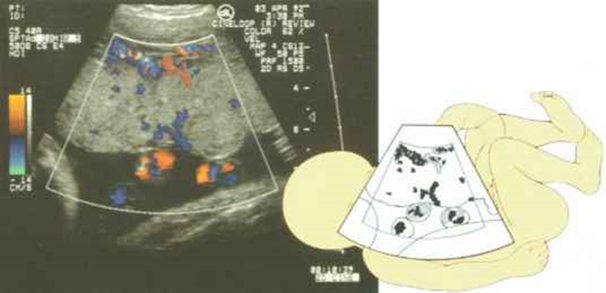
Ultrasound and
color Doppler images of the normal renal arteries and renal veins. |
|
|
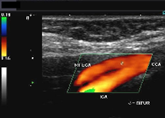
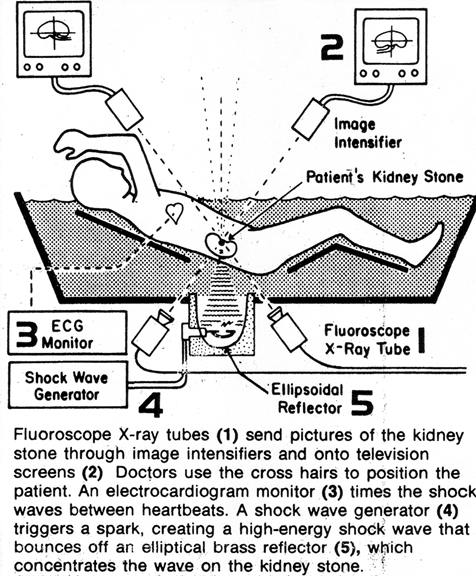
Shock waves are high energy waves. For example, high energy ultrasonic
waves can be used to smash kidney stones in a procedure called extracorporeal shock wave lithotripsy.
|
|
|
|
|
SOUND
LEVELS A relationship between the subjective
sensation loudness and the physical measurable quantity intensity can be made
using a logarithmic scale called the decibel scale [dB] because
the
sensation of loudness is approximately logarithmic in the human ear. Sound Level where
Sound levels for a variety of sounds
Threshold of hearing: The faintest sounds the human ear
can detect at a frequency of 1 kHz have an intensity of about 1x10-12
W.m-2. Threshold of pain: the loudest sounds the human ear can
tolerate have an intensity of about 1 W.m-2. Listen to a set of pure tones (single frequency /
monochromatic audio signals) ONLINE TONE GENERATOR: play with sounds test your
hearing |
|
Example 1 A point source of
sound waves emits a disturbance with a power of 50 W into a surrounding
isotropic-homogeneous medium. Determine the intensity of the radiation at
distances of 1.00 m, 2.00 m and 10.0 m from the source. How much energy
arrives on a small detector 1.0 m from the source with an area of 123 mm2
held perpendicular to the flow in 10 s? Solution P = 50 W R1 = 1.00 m I1
= ? W.m-2 AD = 123 mm2 = 123x10-6 m2 R2 = 5.00 m I2
= ? W.m-2 R3 = 10.0 m I3
= ? W.m-2 The intensity decreases with distance
from source according to the inverse square law I1 = 4.0 W.m-2 I2
= 1.0 W.m-2 I3
= 0.04 W.m-2 At the detector R
= 1.0 m: time interval power PD = ? W energy
PD = 4.9x10-4
W |
|
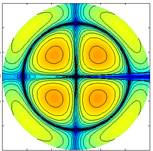
Example 2
|
If you have any feedback, comments, suggestions or corrections please email:
Ian
Cooper School of Physics University of Sydney
ian.cooper@sydney.edu.au