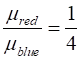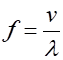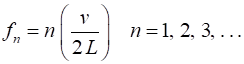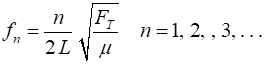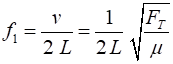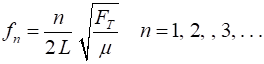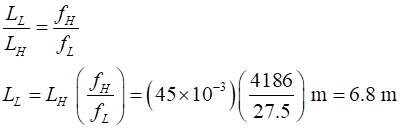|
|
WAVES MUSICAL INSTRUMENTS STRINGS |
How
do we make musical sounds?
|
To make a sound, we need
something that vibrates. If we want to make musical notes, you usually need
the vibration to have an almost constant frequency, that means stable pitch.
Many musical instruments make use of the vibrations of strings to produce the
notes.
Fig.
1. Various string instruments. What do all these
instruments have in common? What
factors determine the pitch of the sound made by plucking, bowing or striking
a string? The physics of the stringed musical
instruments is very simple. The notes played depend upon the string which is
disturbed. The string can vary in length, its tension and its linear density
(mass / length).
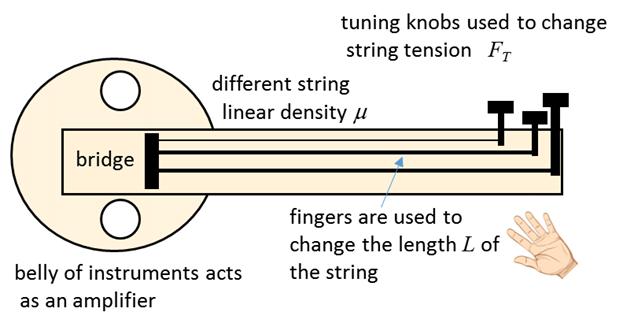
Fig.2. Sketch of a string instrument. String
parameters: length
Length
Linear density
String tension It is only these three factors
and how the string is disturbed that determines the vibrations of the string
and the notes that it plays. A string is disturbed and this
sets up transverse waves travelling backward and forwards along the string
due to reflections at the terminations of the string. The terminations act as
nodes where the displacement of the string is always zero. Only for a set of discrete
frequencies, (natural or resonance frequencies of the string) can large
amplitude standing waves be formed on the string to produce the required
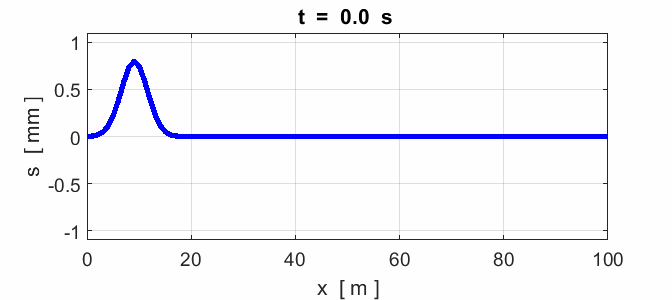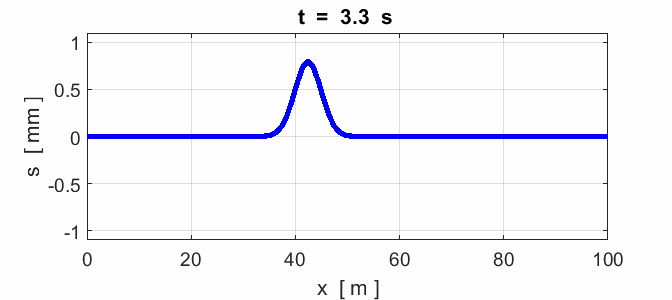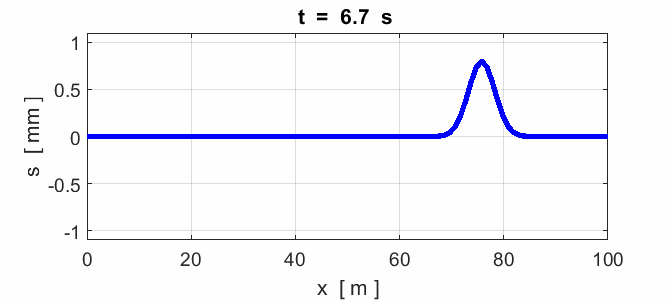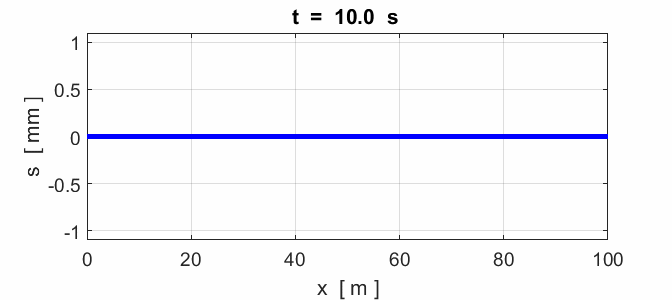
notes. The frequency (1) The speed (2) A steel piano string has a
length of 0.400 m and a mass of 3.00x10-3 kg. A piano tuner
adjusts the string tension to 800 N. What is the speed of the wave on the string?
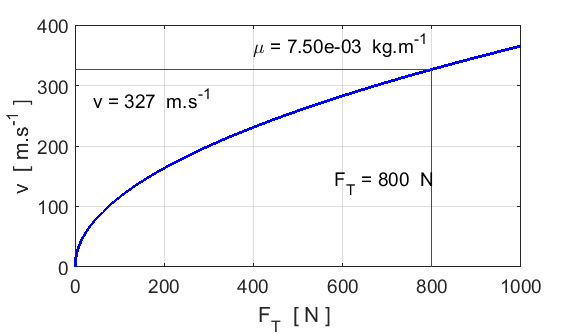
Fig.
3. Variation in the propagation speed
with the string tension for a constant linear density. When the piano tuner adjusts the frequency,
they are making small changes in the propagation speed.
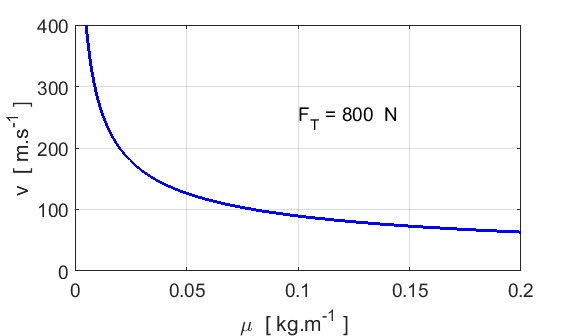
Fig.
4. Variation in the propagation speed
with the linear density for a constant string tension. The smaller the value
of the linear density, the greater the speed. |
|
Fig. 5. Propagation of
pulses along two strings with different linear densities but under the same
tensions. What is the ratio
of the linear densities for the two strings? Answer: N.B. the different time scales for the blue
and red pulses |
|
The Estonia-Minion, a small
grand piano has 88 strings arranged over a sound board (figure 6). To excite a
string to vibrate, it is struck with a hammer. The interaction when the
string is struck with the hammer plays a very important role for the tone
quality of the notes played. The low notes (bass) are played with the long
strings and the high frequencies (treble) are played using the shorter
strings.
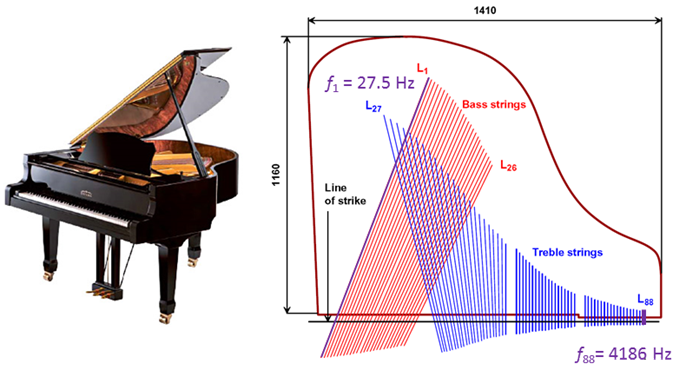
Fig.
6. Estonia-Minion Piano: Position of strings over the soundboard.
There are 88 strings. The longest string L1 plays a note of 27.5 Hz and the
shortest string L88 plays the note 4186 Hz. String L1 f = 27.5 Hz L = 1239 mm FT = 1350 N String L26 f = 130.8 Hz L = 831.2 mm FT = 625 N |
Reflection of waves at boundaries and standing waves
|
The reflections of the waves at the
boundaries of the string are a very important aspect in the music that is
played by musical instruments.
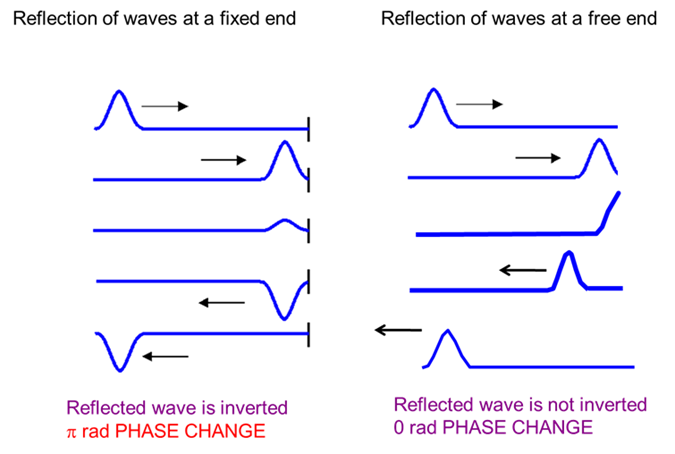
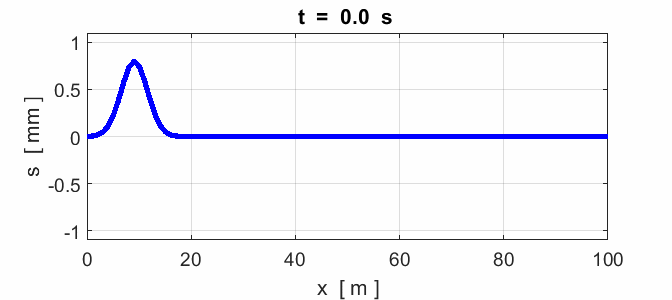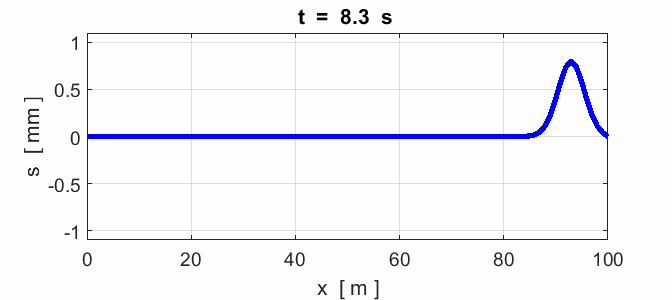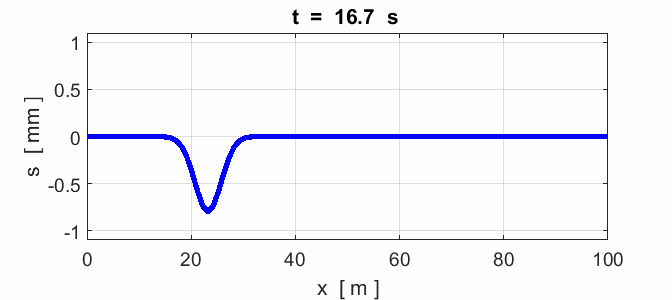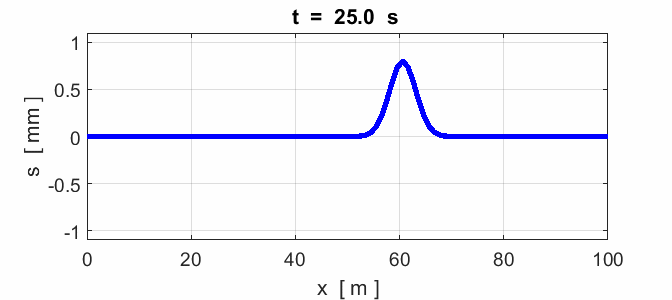
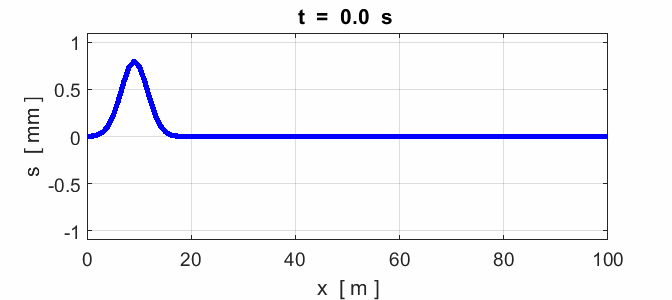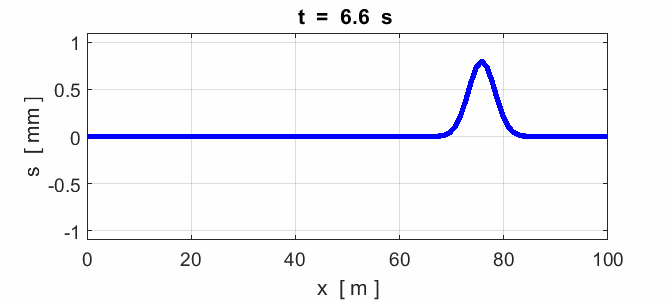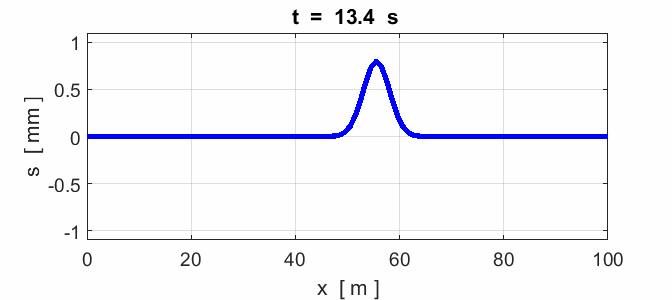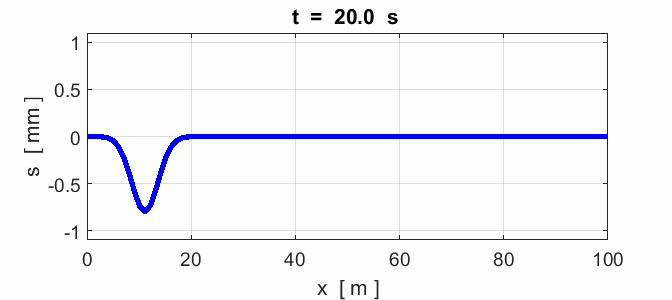
Fig. 7. Reflection of a pulse from a fixed end
(node) and a free end (anitinode).
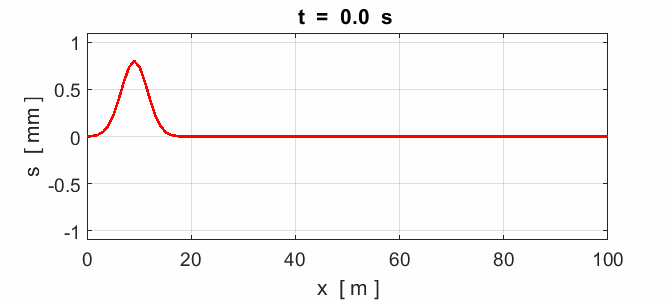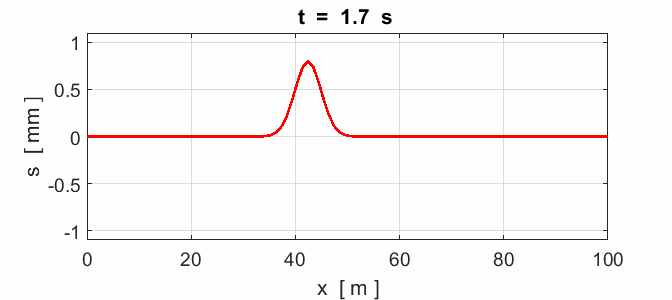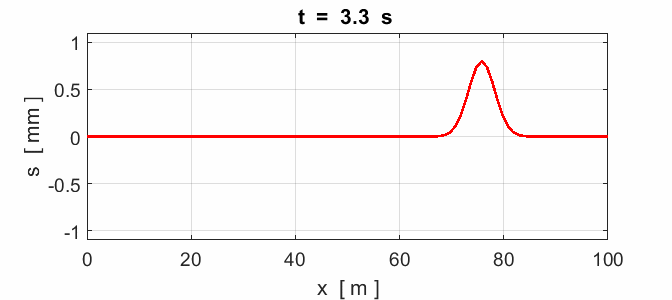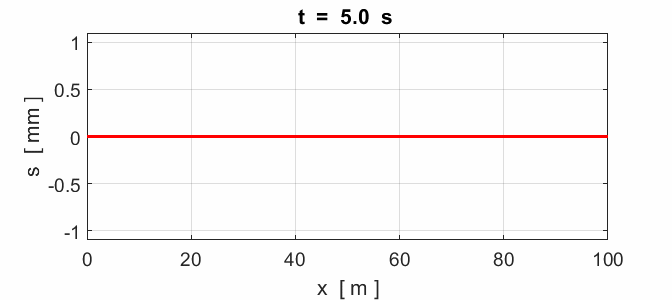
Fig. 8. Reflection of a pulse: x = 0 fixed end (node) and x = 100 m
fixed end (node).
Fig. 9. Reflection of a pulse: x = 0 fixed end (node) and x = 100 m
free end (antinode).
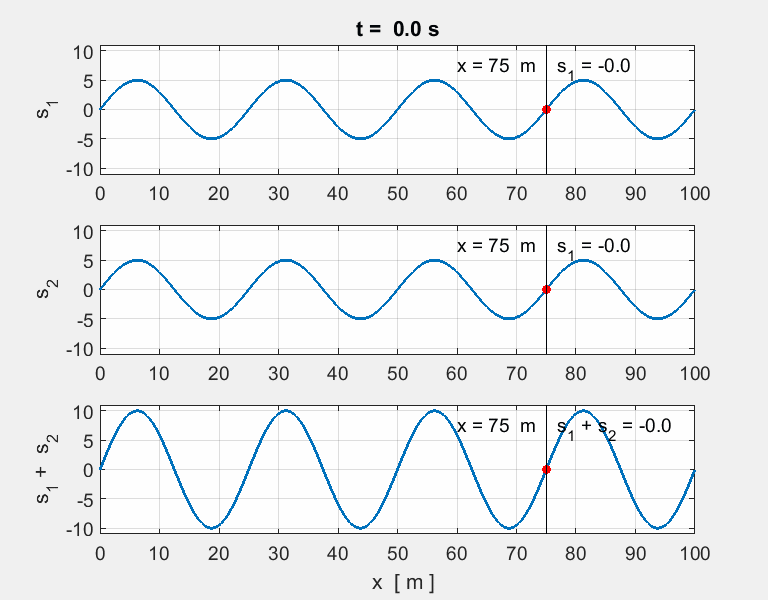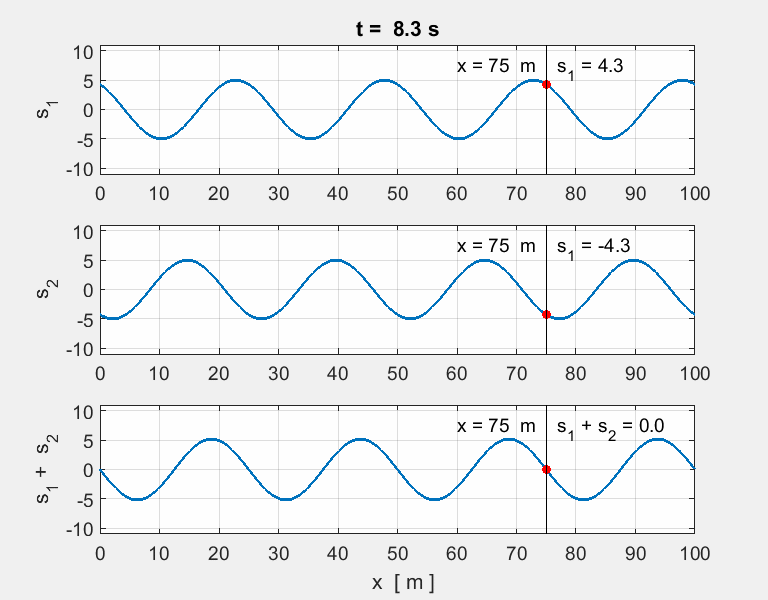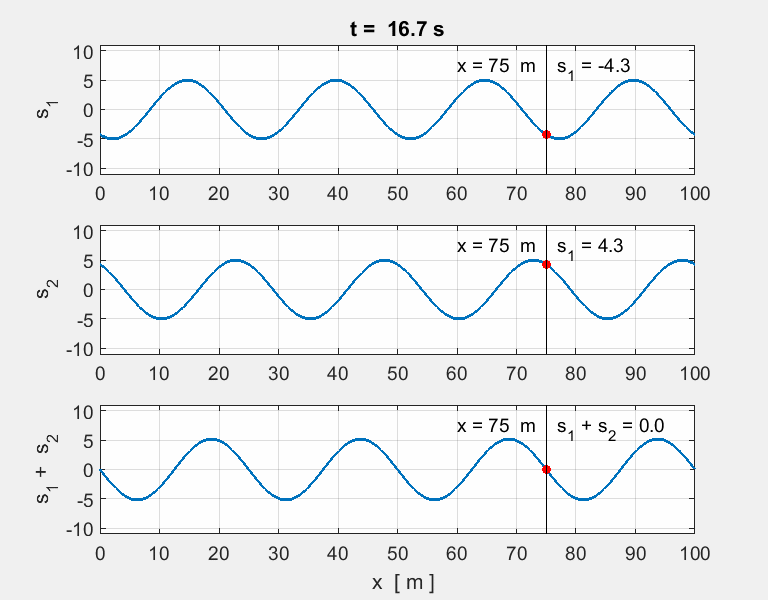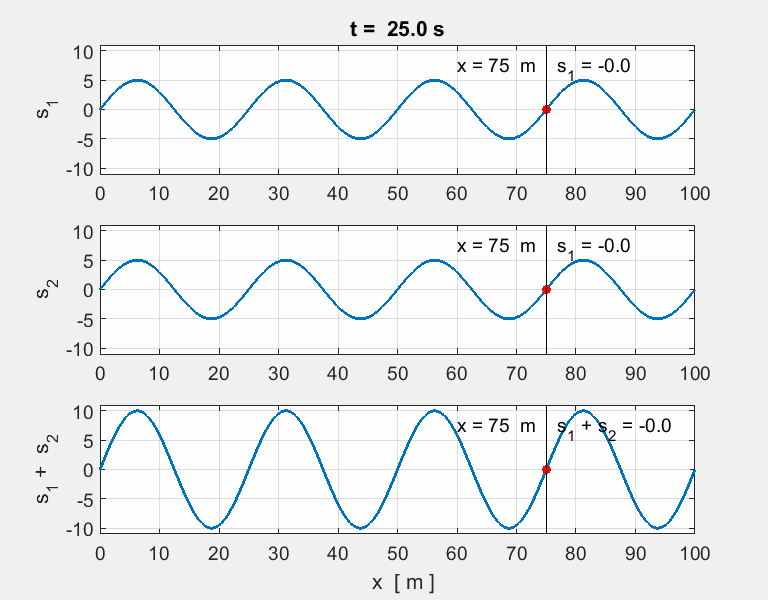
Fig. 10. Colliding pulses. The superposition
determines the resulting shape of the waveform of the two colliding
pulses. Note how the two pulses pass
through each other unaltered. Node at x = 0 and an antinode at x = 100
m. For the waves on strings, the
boundary conditions are always fixed ends, therefore, upon reflection the
wave is always inverted. The ends of the string correspond to nodes. The initial disturbance of the string sets
up waves that travel along the string and are reflected. The resultant
waveform is determined by the superposition of the multiple waves travelling
backward and forward along the string. The resulting oscillation can form standing
waves. The positions where the oscillations reach their maximum
values are known as antinodes. At points where the amplitude of
the oscillation is zero are called nodes these points do not oscillate. Figure 11 shows the resultant standing wave
produced by two waves travelling in opposite direction that have the same
frequency and same amplitude.
Fig.
11. Standing wave due to the
superposition waves two that travel in opposite direction and have the same
frequency and same amplitude. What is the
wavelength of the travelling waves? What is the distance between adjacent
nodes? What is the distance between adjacent antinodes? For a standing wave, the
distance between adjacent nodes or adjacent antinodes is |
|
Exercise REFRACTION A pulse travels along a string and meets a discontinuity where
there is a change in the linear density of the string. The string tension is
uniform along the string. Carefully observe the animation. What is the value of x for the discontinuity? Estimate the
velociites for the incident, reflected and refracted pulses? What is the
change in phase of the reflected and refracted pulses? At the discontinuity, does the linear
density increase or decrease? Explain your answer? Estimate the ratio of the
linear densities
Fig. 12. Refraction of a
pulse at a discontinuity due to a change in linear density of the string. Answers discontinuity at x = 60 m Reflected pulse: rad
change in phase (inverted) Refraction pulse: 0 rad change in phase (upright) Since the reflected pulse is inverted, discontinuity acts like a
fixed end, therefore, the linear density must increase. |
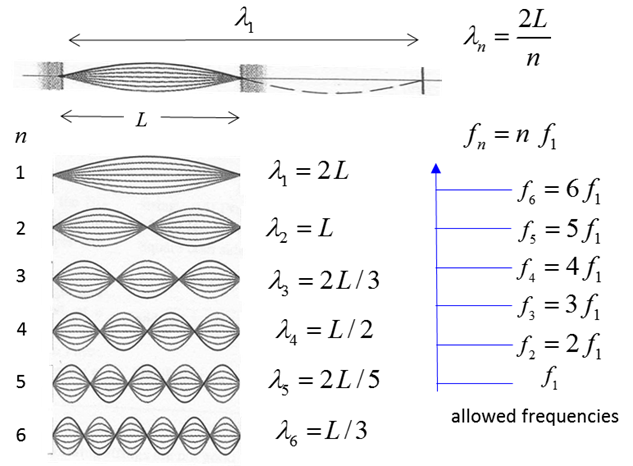
Oscillations of a string
|
When transverse oscillations are
produced in a stretched string fasten at both ends, standing waves are setup.
There must be nodes at the positions where the string is fastened. Hence,
only oscillations are produced with appreciable amplitude when an integral
number of half-wavelengths fit into the length of the string. This gives the
condition (3) Therefore, from equation 1, the
frequencies of the standing waves that can vibrate with appreciable
amplitudes are (1) (4a) The velocity (2) The frequencies (4b) The fundamental frequency (5) The natural frequencies are
integral multiples of the fundamental frequency (6) The natural frequencies are also
called the harmonics:
1st harmonic n = 1 fundamental
2nd harmonic n = 2
nth
harmonic The number n is called the mode number,
and the value of n gives the natural
or normal
mode of the oscillation. The oscillations of the string
are remarkable in the respect that according to classical physics, we get
discrete values of one of the quantities characterizing the oscillations
the frequency. Such a discrete nature is an exception for classical physics.
For quantum processes, it is the rule rather than the exception.
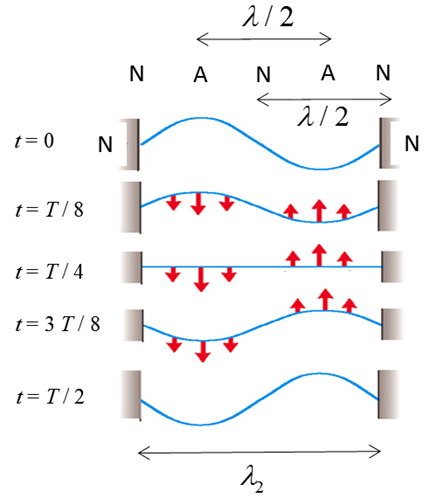
Fig. 13. Normal modes of vibration of a string
fixed at both ends. The standing waves pattern has a series of nodes at fixed
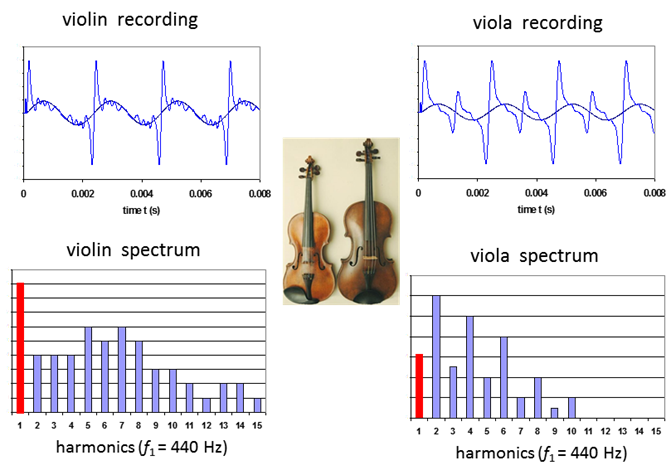
positions that are separated by the distance A musical tone is a steady periodic sound. A musical tone is characterized
by its duration, pitch (frequency), intensity (loudness), and timbre or
quality. Timbre or quality describes all the
aspects of a musical sound other than pitch or loudness. Timbre is a
subjective quantity and related to richness or perfection music maybe
heavy, light, murky, thin, smooth, clear, etc. For example, a note played by
a violin has a brighter sound than the deeper sound from a viola when playing
the same note (figure 14). A simple tone or pure tone, has a sinusoidal
waveform. A complex tone is a combination of two or more pure tones that have
a periodic pattern of repetition. When the string of a musical
instrument is struck, bowed or hammered, many of the harmonics are excited
simultaneously. The resulting sound is
a superposition of the many tones differing in frequency. The fundamental
(lowest frequency) determines the pitch of the sound. Therefore, we have no
difficultly in distinguishing the tone of a violin and the tone from a viola
of the same pitch a different combinations of harmonic frequencies are
excited when the violin and the viola the play same note (figure 14).
Fig.
14. The sound recordings for a violin
and viola playing the same note at a pitch of 440 Hz. The sounds from the two
instruments have a different frequency spectrum. The violin has a richer
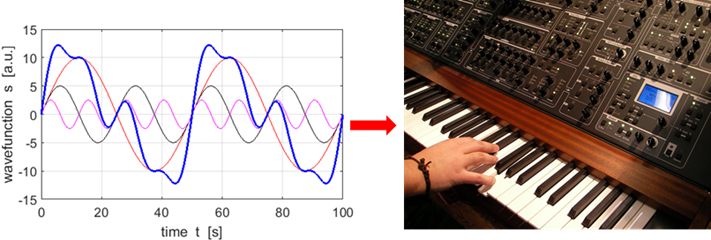
sound because many more higher harmonics are excited. The French mathematician Joseph
Fourier discovered a mathematical regularity in periodic wave forms. He found
that even the most complex periodic wavefunction can be dissembled into a
series of sine wave components. The components correspond to sine functions
of different frequencies and amplitudes and when added together reproduce the
original wavefunction. The mathematical process of finding the components is
called Fourier
Analysis. Figure 14 shows the component frequencies for the sound
recordings of the violin and viola. Fourier
synthesis is
a method of electronically constructing a signal with a specific and desired
periodic waveform from a set of sine functions of different amplitudes and
that have a harmonic sequence of frequencies. Fourier
synthesis is used in electronic music applications to generate waveforms that
mimic the sounds of familiar musical instruments.
Fig. 7. Fourier synthesis
and an electronic music synthesizer.
|
|
Exercise A guitar string is 900 mm long
and has a mass of 3.6 g. The distance
from the bridge to the support post is 600 mm and the string is under a
tension of 520 N. 1 Sketch the shape of the wave for the
fundamental mode of vibration. 2 Calculate the frequency of the
fundamental. 3 Sketch the shape of the string for the
sixth harmonic and calculate its frequency. 4 Sketch the shape of the string for the
third overtone (fourth harmonic) and calculate its frequency.
f1= 300 Hz f6= 1.8103Hz
f4= 1.2103Hz Answers: |
|
Exercise A violin string plays at a
frequency of 440 Hz. If the tension is increased by 8.0%, what is the new
frequency? Answer: 457 Hz |
|
Exercise A string has a mass per unit
length of 2.50 g.m-1 and is put under a tension of 25.0 N as
it is stretched taut along the x-axis. The free end is attached to a tuning
fork that vibrates at 50.0 Hz, setting up a transverse wave on the string
having an amplitude of 5.00 mm. Determine the speed, angular frequency,
period, and wavelength of the disturbance. Answers: 100 m.s-1, 3.14x102
rad.s-1, 2.00x10-2 s, 2.00 m |
Stringed Instruments
|
The natural frequencies of
vibration of a string are given by (4a) A stringed instrument is tuned
by adjusting the tension of the string. This changes the speed of the
transverse waves travelling along the string, hence changing the frequency of
vibration. When a finger is placed on a violin string, the effective length
of the string is shorter. So, its fundamental frequency (pitch) is higher
since the wavelength of the fundamental is also shorter. The strings on a
violin are all the same length. They sound at different pitches because the
strings have different linear densities (mass / length), which affects the
speed and hence frequency. The greater the linear density of a string, the
smaller the speed and so the pitch is lower for the same length of string. In
piano and harps, the strings are different lengths. For the lower notes, the
strings are not only longer, but also heavier as well. |
|
Example Estonia-Minion Piano the
highest note played on the piano is 4186 Hz and the lowest note is 27.5
Hz. If the string for the highest note
is 45 mm long, how long would the string be for the lowest note if the two
strings have the same linear density and under the same tension. Solution The linear density and the
tensions in the two strings are the same and for the fundamental n = 1 Therefore where the subscripts L and H
refer to the low note and the high note respectively. The answer of 6.8 m is ridiculously long for a piano the
longer strings for the low notes must be made heavier, so that on even grand
pianos, the strings are less than 3 m long. |
|
If you have any feedback, comments, suggestions or corrections
please email: Ian Cooper School of
Physics University of Sydney ian.cooper@sydney.edu.au |