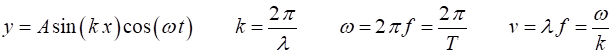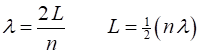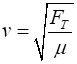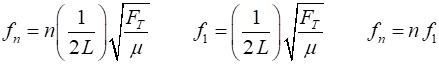|
|
WAVES RESONANCE Forced Vibrations
of a String
|
STANDING WAVES
|
When a taut
string fixed at both ends is disturbed, travelling waves propagate until they
reach the ends where they are reflected and travel back along the string.
Each such reflection gives rise to waves travelling in opposite directions.
The waves along the string interfere with each other according to the
principle of superposition. Standing
waves can
be setup along the string where all points execute simple harmonic motion
with the same phase and frequency. A standing wave is described by (1) For a string of length (2) Hence, the allowed wavelengths
of the string are (3)
For a standing wave, multiples
of The speed of propagation (4)
Using equations (1), (2) and
(3), it is clear that the frequencies for the
vibration the standing waves in the string form a harmonic series where (5) and |
RESONANCE
|
In general, whenever a system capable
of oscillating is acted upon by a series of impulses (driving force) having
frequency equal to nearly equal to one of the natural frequencies of
oscillation of the system, then, the system can oscillate with relatively
large amplitude. This phenomenon is called resonance and the system is
said to resonate. |
SIMULATIONS
|
Image a taut string being
clamped at one end (node) but shaken up and down at a constant frequency
In the modelling of the vibrating
string driven by an external force acting on it, the driven end of the string
behaves approximately as a node and all dissipative forces are ignored. When
the driving force matches any of the natural frequencies of vibration of the
string, energy is continually being transferred from the driver to the
string, as a consequence the amplitude of the
oscillation grows and grows with time. |
|
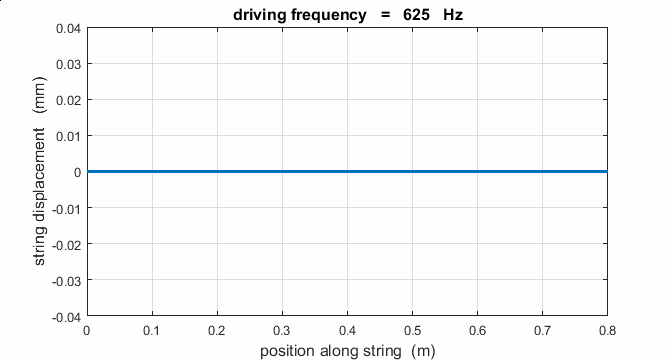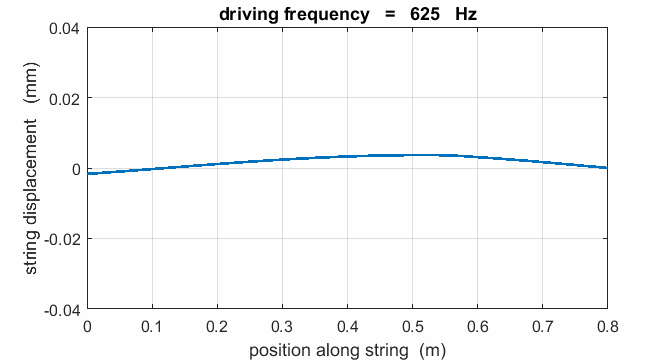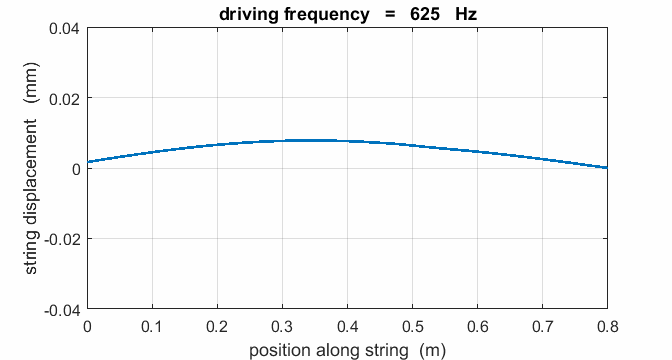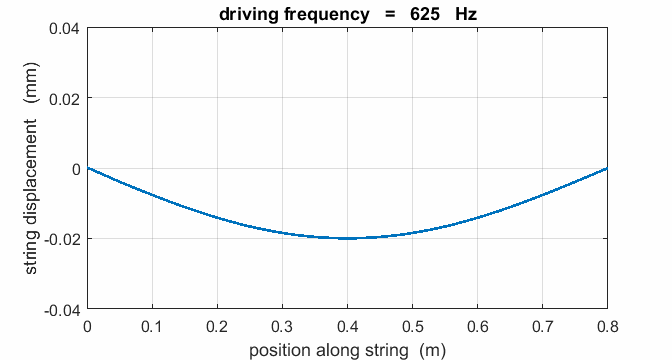
Exercise String parameters: length L = 0.800 m string tension FT =
400 N Linear
density m = 4.00x10-4 kg.m-3
Show that the fundamental frequency is f1 =
625 Hz and the speed of the transverse waves along the string is v = 1000 m.s-1.
Calculate the natural frequencies of vibration for the first 6
harmonics.
Sketch the shape of the taut string for these 6 normal modes.
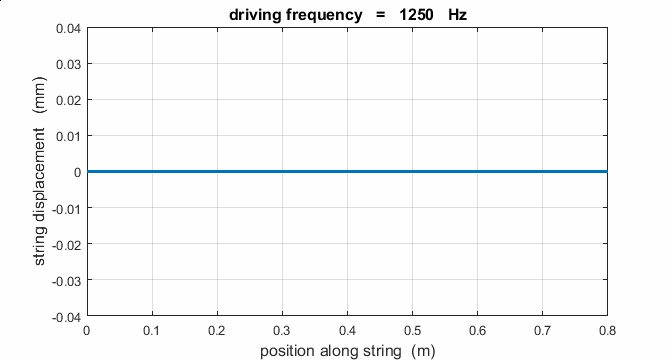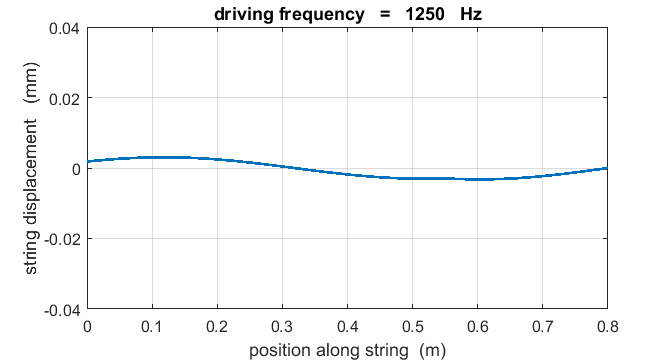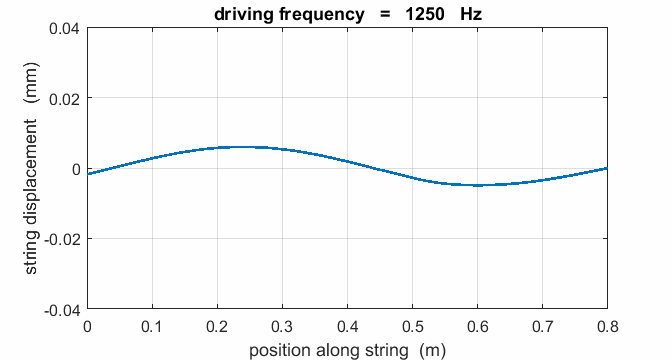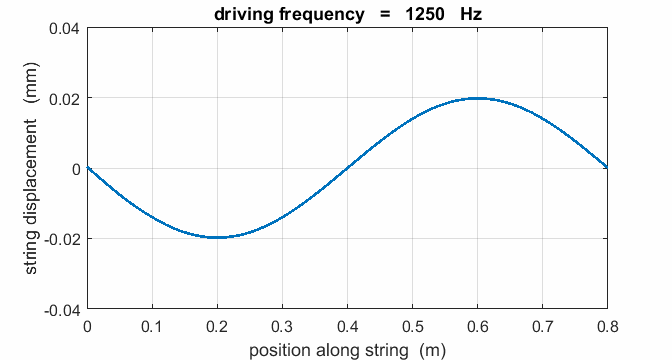
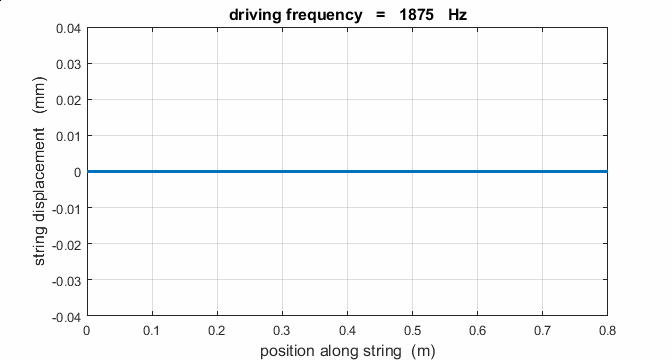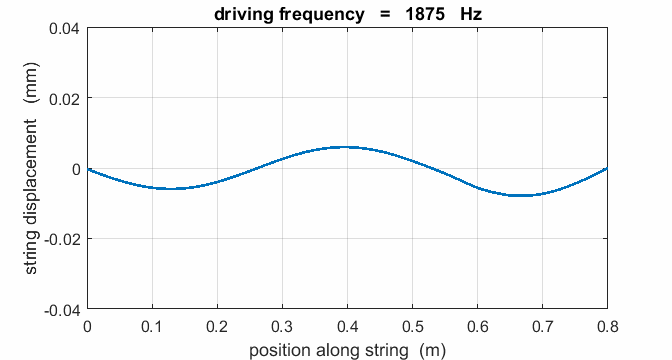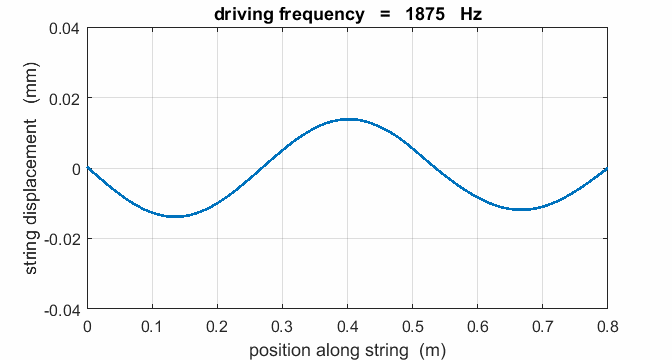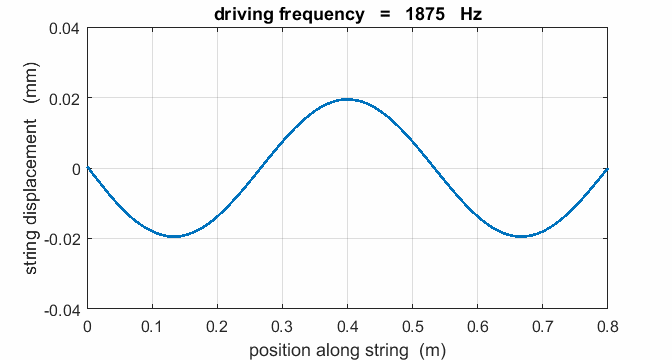
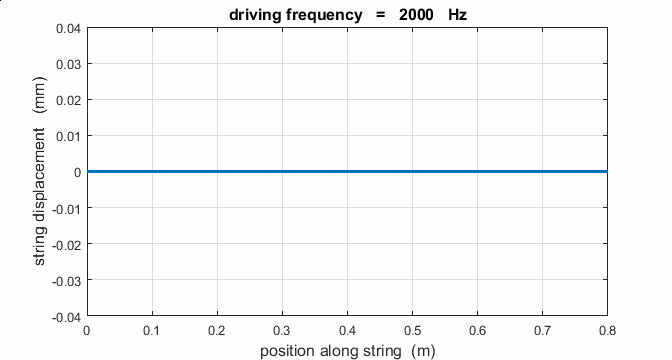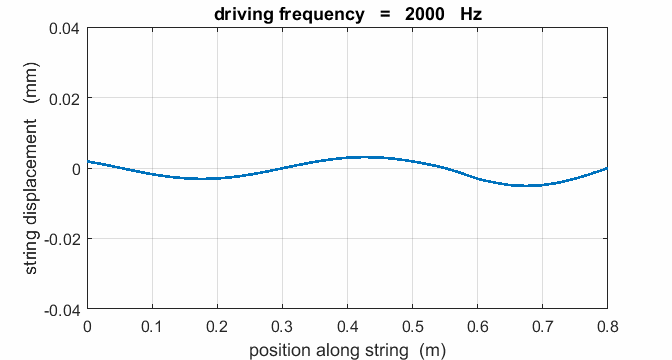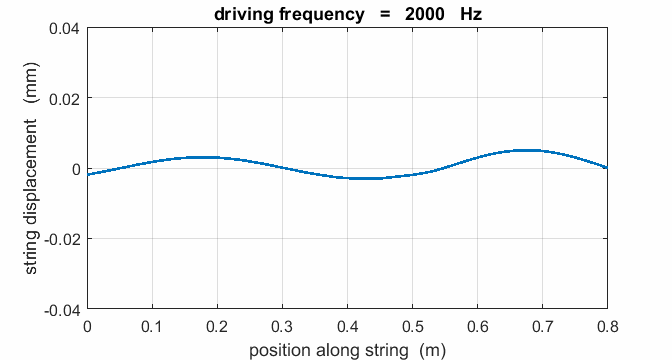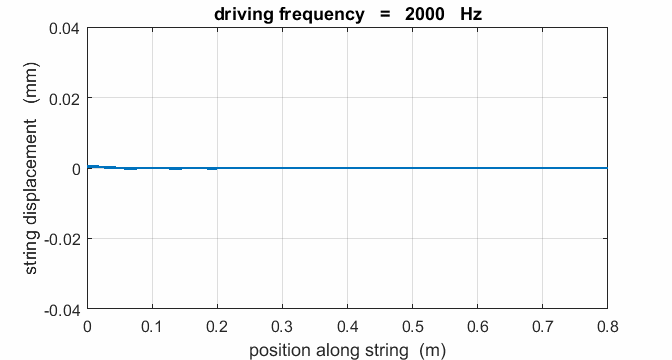
If a string is driven at a frequency PREDICT OBSERVE
EXPLAIN (P O
E) Predict the
responses of the string driven at a frequency of 500 Hz, 625, Hz, 1000 Hz,
1250 Hz, 1875 Hz, 2000 Hz, 2500 Hz, 3125 Hz, and 3750 Hz. Observe the
animations of the driven string. Compare your predictions with your observations and Explain any discrepancies. |
Make your predictions before viewing the animation below
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
For a true standing wave, the
nodes occur at fixed locations along the string and are points where the
string is permanently at rest. Hence, energy is not transported along the string
to the right or left. The energy remains standing in the string as energy
is continually being transferred between elastic potential energy and
vibrational kinetic energy in the region between the nodes. Also, between
nodes, all point vibrate in-phase. In our simulation of the
strings vibrations the end at x = 0 is not
a true node since this end of the string does not remain permanently at
rest. If you carefully observe the animated motion of the string you will
also see that there are no true nodes. There cant be true nodes as energy
must flow along the string from the stimulus driving the oscillations at the
end of the string. Energy is continually added to the string by a vibrator,
building up the amplitude of the oscillation only at or near one of the
natural frequencies of vibration. When the string is excited at a frequency
well away from a natural frequency, the reflected waves reaching the end of
the string at x = 0 are out of phase with the external vibrator, hence energy
can be transferred from the string back in to the vibrator. The wave pattern
is not fixed but wiggles about. On average, the amplitude of the oscillation
is small and not much different from that of the vibrator, and the string
vibrates at the driving frequency. Hence, the string absorbs maximum energy
from the vibrator at resonance. Tuning a radio is an analogous process: the
circuit resonates with the transmitted signal and absorbs peak energy from
the radio signal. |
|
If you have any feedback, comments, suggestions or corrections
please email: Ian Cooper School of
Physics University of Sydney ian.cooper@sydney.edu.au |