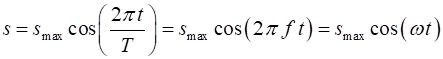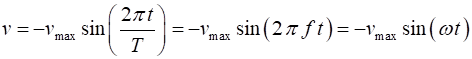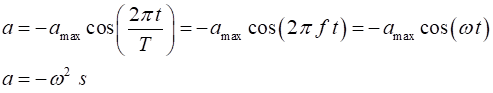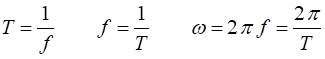|
WAVES SIMPLE HARMONIC MOTION VIBRATIONS
(OSCILLATIONS)
Anything that moves back and forth, to or fro, side to
side, in-out-in, or up or down is said to be vibrating or oscillating.
Time variations that repeat themselves at regular intervals: periodic or cyclic behavior.
Fig. 1. Identify all the vibrations in the
pictures. A vibration is a periodic wiggle in time. A wave is a periodic wiggle in both space and time. The source of all waves is something that is
vibrating. Light and sound are
both vibrations that propagate through space as a wave, but are two very
different types of waves. |
|
VIBRATIONS (OSCILLATIONS)
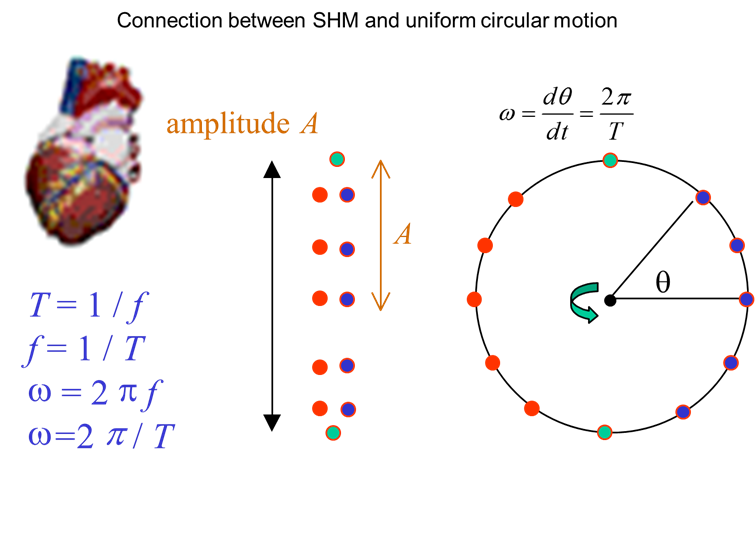
SIMPLE HARMONIC MOTION (SHM) To model vibrations, we need to setup
a simple model using approximations and simplifications. The simplest model
to describe vibrations is called simple harmonic motion. In this model, the
object will move backward and forward in a straight line about an equilibrium
position with a period which is independent of the magnitude of the
disturbance and the displacement of the object from its equilibrium position
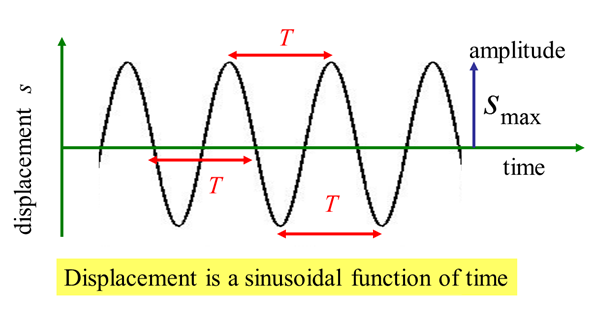
can be described by a sinusoidal function. For the vertical
oscillations of an object, the frame of reference has the +Y axis pointing
upwards and the equilibrium position corresponds to the Origin. The position
of the object at any time t is given by the displacement Displacement Velocity Acceleration Displacement amplitude Velocity amplitude Acceleration amplitude
The amplitude is always a
positive number. The symbol
For SHM the acceleration
is proportional to the displacement and it direction is opposite to the
displacement. Period Frequency
1
kHz = 103 Hz (kilo) 1 MHz = 106 Hz (mega) 1GHz = 109 Hz (giga) Angular
frequency
Phase angle The displacement
|
|
|
|
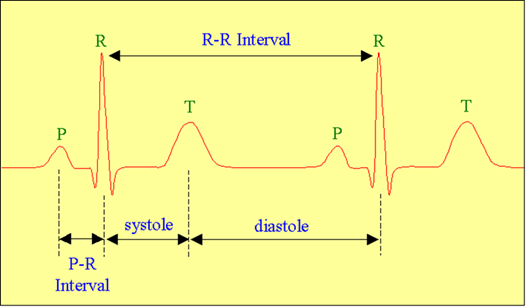
A periodic signal is the recording of an
ECG.
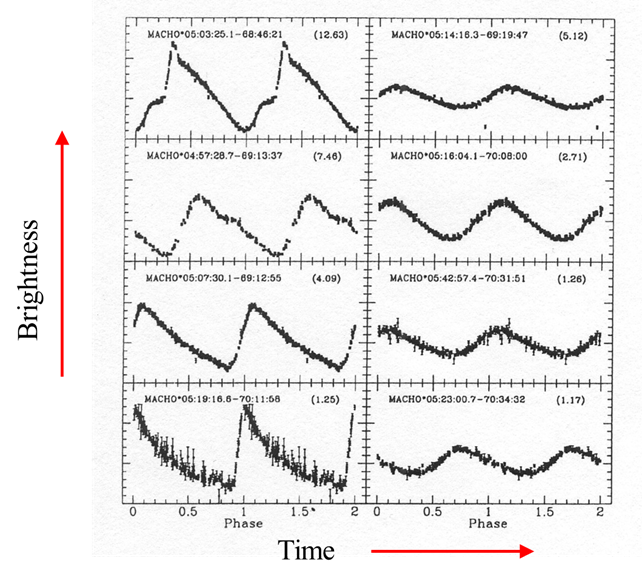
The
brightness of stars varies periodically.
|
|
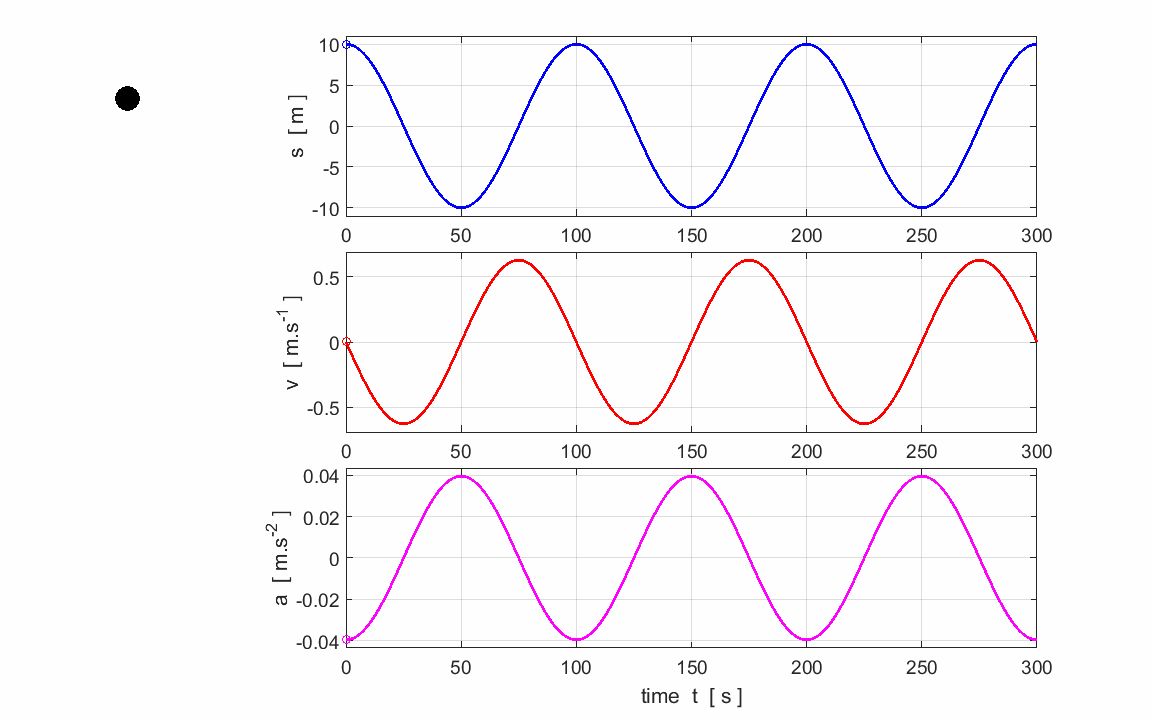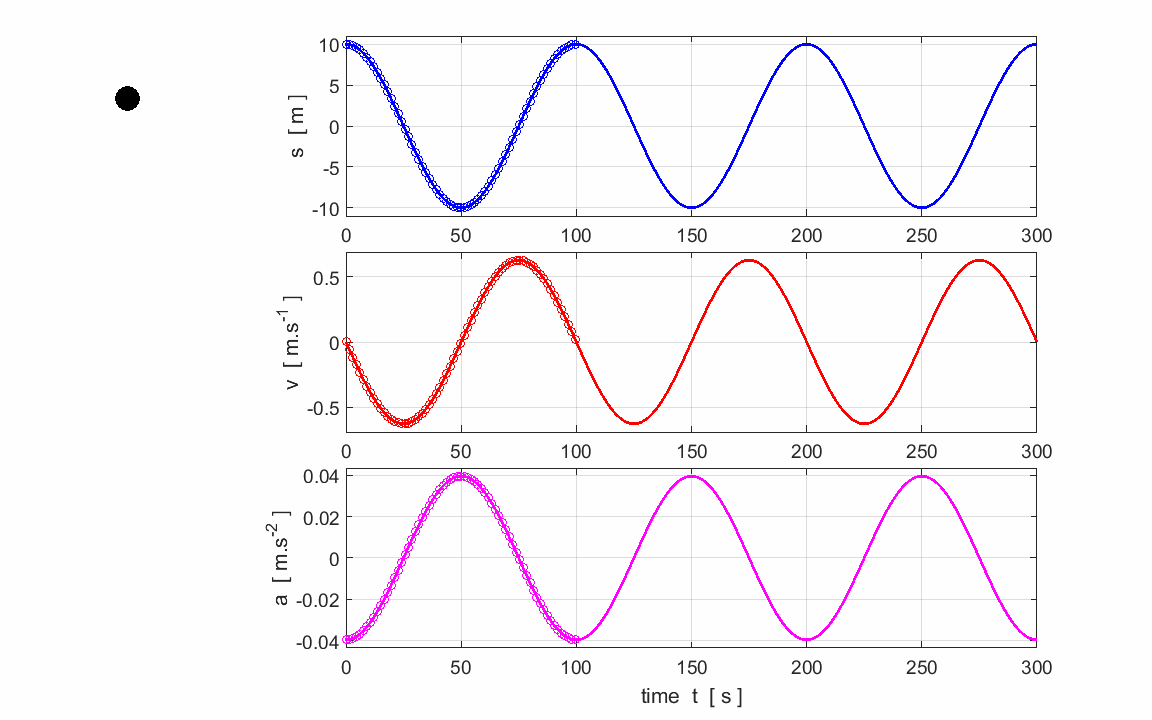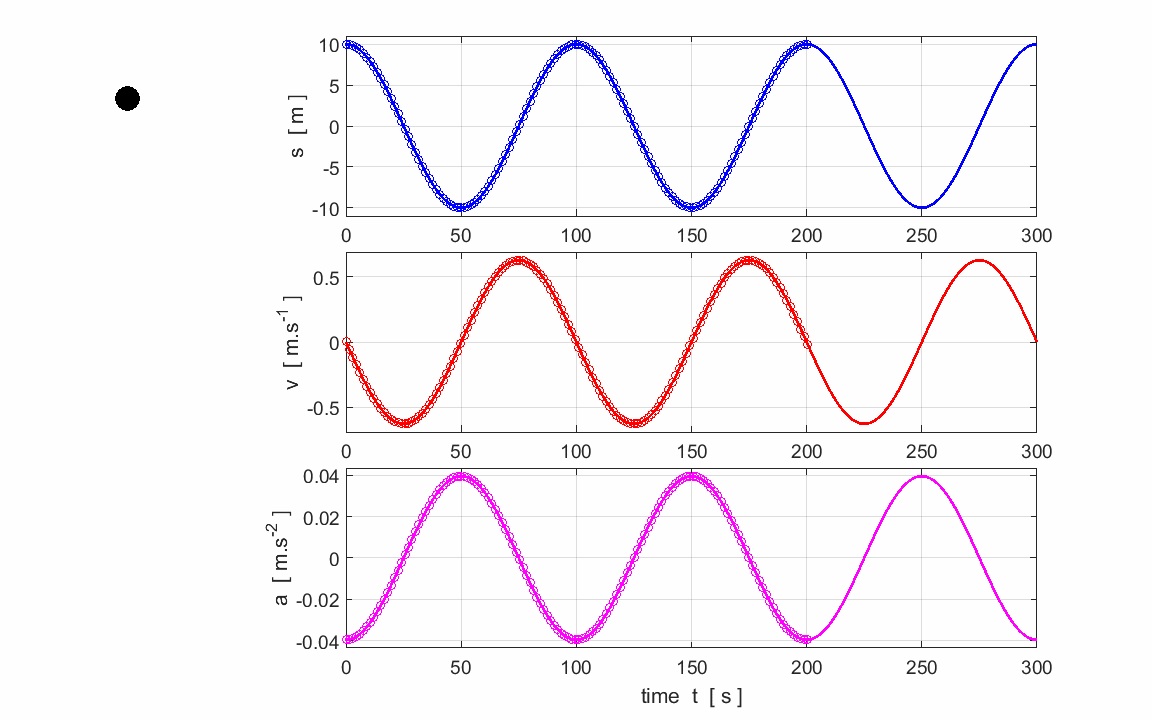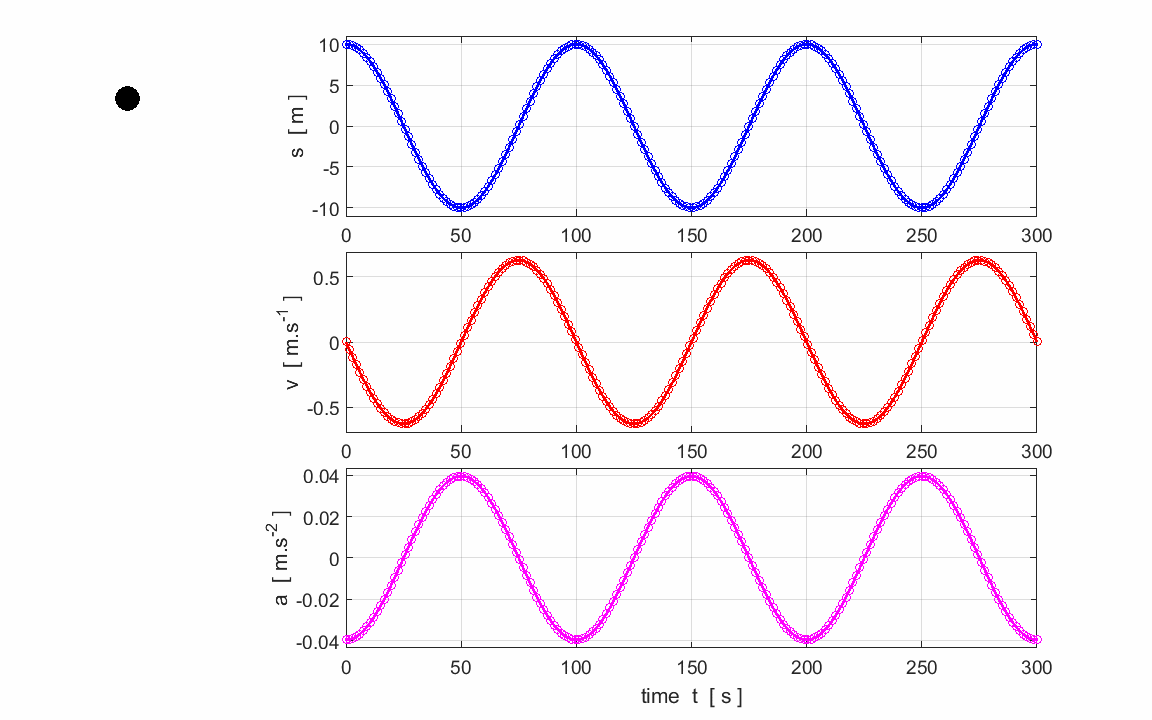
Fig. 2.
An animation for an object executing SHM in the vertical direction. |
|
Exercise 1 Watch the animation and check that the
graphs do successfully describe the motion of the object. Use the graphs to calculate and check
your answers for the estimation of the following parameters:
Period,
frequency and angular frequency
Amplitudes:
displacement, velocity and acceleration The slope of the tangent to a
displacement vs time graph gives the velocity. Verify from the graphs. The slope of the tangent to a velocity
vs time graph gives the acceleration. Verify. Predict the changes in the three
graphs if (1) The amplitude (2) The period |
|
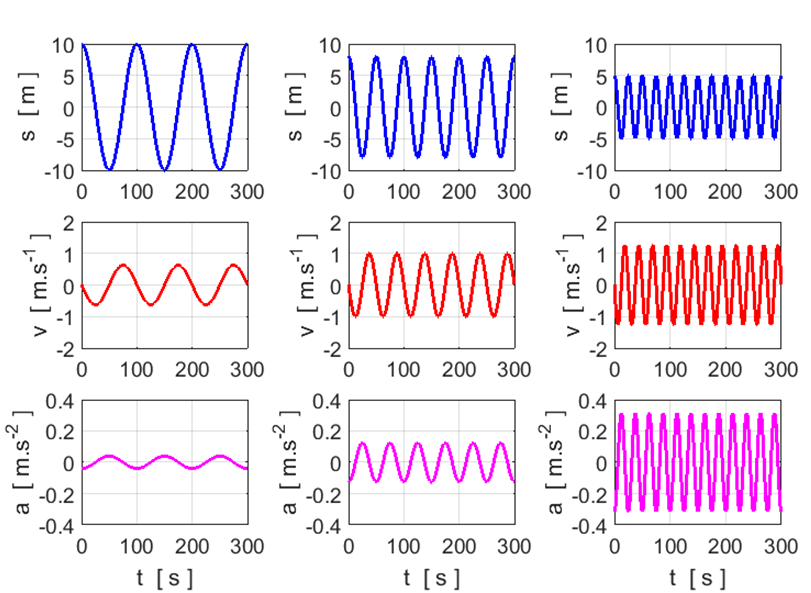
Exercise 2
Use the graphs to calculate and check
your answers for the estimation of the following parameters:
Period,
frequency and angular frequency
Amplitudes:
displacement, velocity and acceleration |
|
Animation
produced with osc_shm_01A.m SHM
graphs produced with osc_shm_01.m If you have any feedback, comments, suggestions or corrections please email: Ian Cooper
School of Physics University
of Sydney ian.cooper@sydney.edu.au |