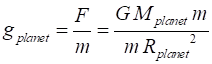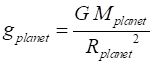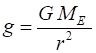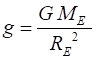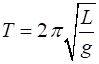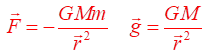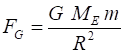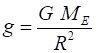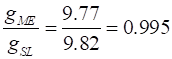MODULE 5
ADVANCED MECHANICS
GRAVITATIONAL FORCES
|
NEWTONS LAW OF UNIVERSAL GRAVITATION Newton's Universal Law of Gravitation states that any two
objects exert a gravitational force of attraction on each other. The
direction of the force is along the line joining the two objects. The
magnitude of the force is proportional to the product of the masses of the
two objects, and inversely proportional to the square of the distance between
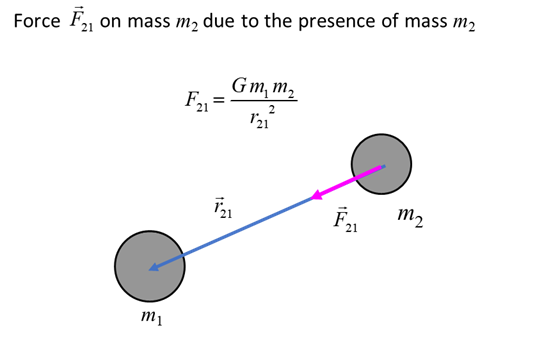
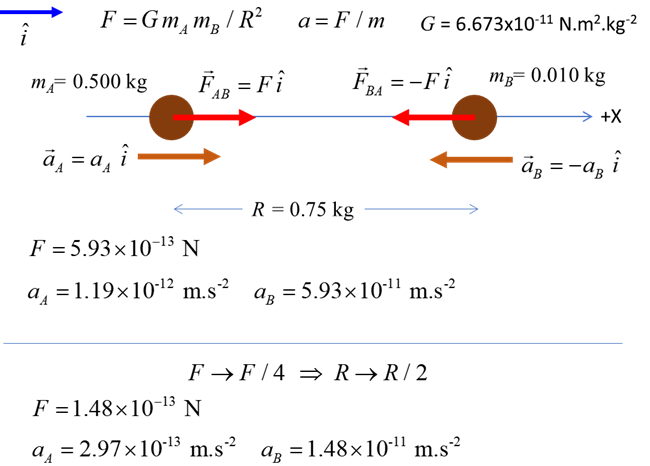
them (figure 1, equation 1). (1) force F [N] mass of the two objects m1 and m2
[kg] distance between the centres of the
two objects r [m] Universal Gravitation Constant G = 6.673x10‐11 N.m2.kg‐2 This equation should not be expressed in terms of vectors. Figure 1 shows why it better not to use vector notation for the
gravitational force.
Fig. 1. Gravitational
force By 1687, Newton had formulated his ideas and unified centuries
of astronomical observations into a coherent theory of gravity in his famous
book Philosophiae Naturalis
Principia Mathematica. A quote from Newton Every particle in the universe attracts every other particle with
a force that is directly proportional to the product of their masses and
inversely proportional to the square of the distance between them. For
any calculations, we can take the mass of an object being concentrated at a
point known as the centre of mass. For example, we take the geometric
centres to determine the separation distance between two planets. The variation of the magnitude of the gravitational force with
separation distance between two objects is shown in figure (2).
Fig.2. Gravitation force as a function of
separation distance. The graph shows the inversely proportional relationship
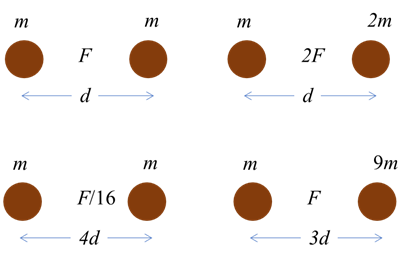
between force and separation distance. Figure 3 shows how the force is
dependent upon the masses of the two objects and their separation distance.
Fig. 3. Gravitational force
dependence on mass and distance. Newtons Law of Universal
Gravitation plays a major role in calculations for the motion of rockets,
satellites and the motion of planets around the Sun and the Moon around the
Earth. GRAVIATIONAL FIELD A gravitational
field surrounds every object that has mass, and this field
permeates all of space. A second object of mass m experiences a gravitational force F
in this field. A
field is a region of space where an object experiences a force. For example,
a charged particle will experience a force in an electric field and a moving
charged particle will experience a force in a magnetic field. The strength of the gravitational field is given by the gravitational field strength g
(also called
the acceleration due to gravity) where (2) The S.I. unit for the gravitational field strength g
is N.kg-1
or m.s-2. The gravitational field strength gplanet
at the surface
a planet can be determined from Newtons Law of Universal Gravitation
(equations 1 and 2). Consider an object of mass m at the surface of a planet where Rplanet
is its radius
and Mplanet
is the mass of
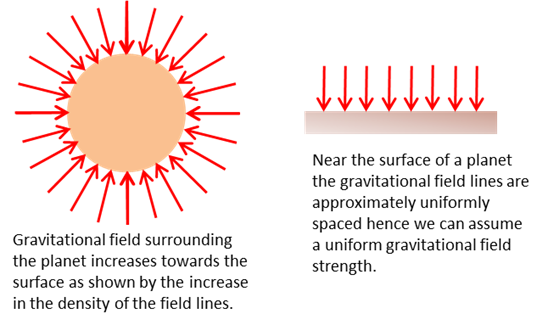
the planet. (3) The gravitational force can be visualised by a pattern of gravitational field lines. The arrow shows the direction of a force on
a mass placed at that point in the field and the density of the field lines
is proportional to the gravitational field strength. Figure (4) shows the gravitational
field surrounding a planet and in a region close to the surface of the
planet.
Fig.
4. Gravitational field surrounding a
planet. The gravitational field strength (or the acceleration due to
gravity) for the Earth (mass ME and radius RE
) is determined
by considering the gravitational force acting of an object of mass m
and distance r
from the centre
of the Earth and Newtons Second Law At the Earths surface, we take the gravitational
field to be constant where r = RE
and the value for the acceleration due to
gravity or gravitational field strength is (4) Earths mass ME = 5.971024 kg Earths radius RE = 6.38106 m
g = 9.7871 m.s-2 The value of g
for
calculations is often taken as 10 m.s-2, 9.8 m.s-2
or 9.81 m.s-2.
Fig.
5. Gravitational field surrounding
the Earth. The magnitudes of the gravitational force, gravitational potential
energy and the gravitational field strength (acceleration due to gravity) all
depend upon the distance between the centre of the Earth and object within
the gravitational field. Experiment Determination of the acceleration due to gravity The period T of oscillation of a simple pendulum
which vibrates with a small amplitude only depends upon the length L of the pendulum and the acceleration
g due to gravity (equation 5) (5) Perform you own experiment to measure g
by varying the
length L of the pendulum and measuring its period T . Hint: Plot a graph of T2 vs L. Web activity and spreadsheet activity Use the
web to find the mass and radius of all the planets, the Sun and Moon. Enter
the data into a spreadsheet and calculate the acceleration due to gravity at
their surfaces and compare their value with g at the surface of the Earth. What affects the value of g variations of g
from 9.8 m.s-2
? Why ?
Changes
in height of the Earths surface mountains & valleys
Distribution
of mass near the Earths surface -
dense mineral deposits
Rotation
of the Earth
(Earth fatter at the equator
gpole
> gequator)
Earth
not a perfect sphere
9.782
m.s-2 (equator) g 9.832 m.s-2 (pole)
altitude
h |
|
Location |
g (m.s-2) |
Altitiude (km) |
g (m.s-2) |
|
Equator |
9.780 |
0 |
9.81 |
|
Sydney |
9.797 |
1 000 |
7.33 |
|
Melbourne |
9.800 |
5 000 |
3.08 |
|
South
Pole |
9.832 |
10 000 |
1.49 |
|
WEIGHT In physics, weight is a
measurement of the gravitational force acting on an object. Near the surface
of the Earth, the acceleration due to gravity is approximately constant; this
means that an object's weight is roughly proportional to its mass. The weight of an object of mass
m is (6)
The weight of an object is the same as the
gravitational force between the object and its central mass.
The weight of an object varies according to the
gravitational field strength (acceleration) that is affected by distance from
the centre of a planet.
Mass is not affected by gravitational acceleration
while weight is. The weight of an object can be
found by measuring the extension or compression of a spring since its
extension and compression are proportional to the mass of the object. It some textbooks weight is
defined as the force exerted on a support as shown in figure (5).
Fig. 5.
Weight of an object can be found by measuring the extension or
compression of a spring. Note:
The equations given in the Physics Stage 6 Syllabus are incorrect you simply cannot divide
by a vector |
|
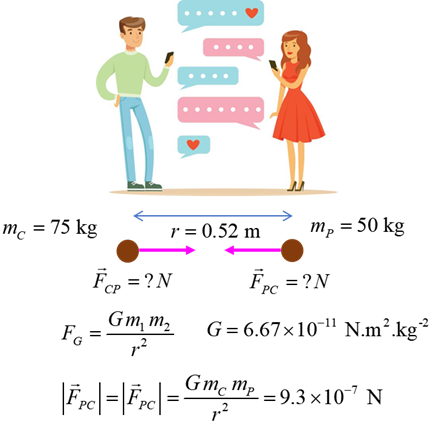
Example 2 Gravitational Force attraction between
people Chris has a mass of 75 kg and Pat has a mass of 50 kg are standing
near each other a distance 0.52 m apart. Are they attracted to each other and
how strong is the attraction? Solution 1 THINK: how to approach the problem / type of problem /
visualize the physical situation / annotated scientific diagram / what do I
know! The two people are attracted by the gravitational force. We can
calculate the magnitude of the force using Newtons Law of Universal
Gravitation
The answer is
that the gravitational attraction is very small |
|
Example 3 Acceleration due to gravity (gravitational
field strength) Compare the acceleration due to gravity (gravitational field
strength) at sea level and at the top of Mt Everest. radius of the
earth height of Mt
Everest Solution 3 THINK: how to approach the problem (ISEE) / type of problem /
visualize the physical situation / annotated scientific diagram / what do I
know!
Newtons Law of gravity between the Earth and an object of mass
m is The gravitational force can be expressed in terms of the
gravitational field strength g Hence, the gravitational field strength (acceleration due to
gravity) is At sea level, At top of Mt Everest, Ratio of the two accelerations
due to gravity A very small difference, however, we have ignored the extra mass that sits under the top of Mt Everest. |
|
Ian Cooper School of Physics University of Sydney If you have any feedback, comments,
suggestions or corrections please email Ian Cooper ian.cooper@sydney.edu.au |