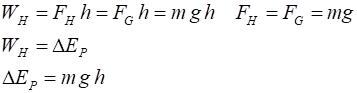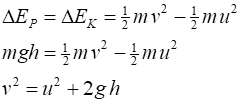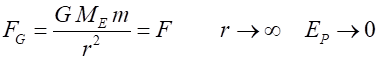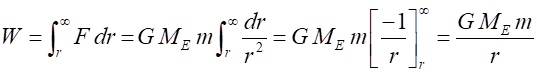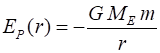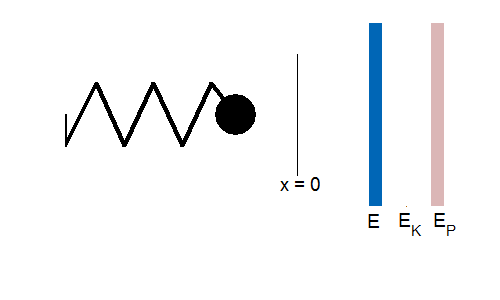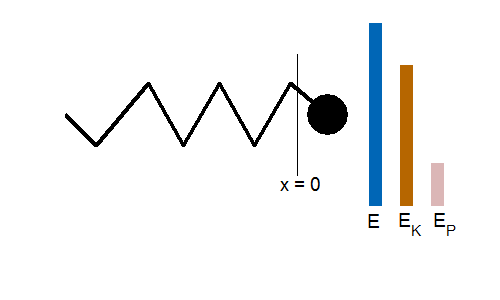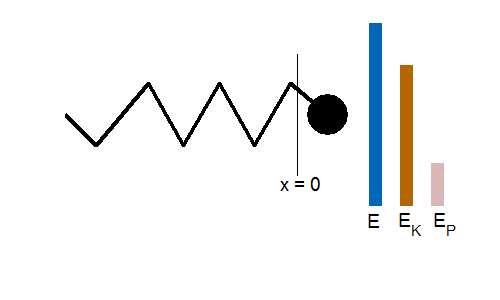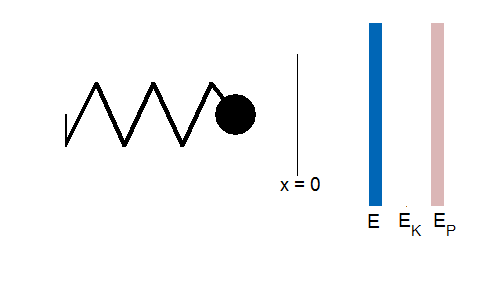MODULE 5
ADVANCED MECHANICS
GRAVITATIONAL POTENTIAL
ENERGY
|
Work W [ J ] When
a force acts on an object over a distance work is done on the object to
change its kinetic energy or potential energy. Gravitational Potential Energy
EP U
UG [ J ] Consider lifting an object of mass m
with your hand
so that its kinetic energy does not change (object rises at a constant
velocity, a = 0). Work W is done by the hand on the object
increasing the gravitational potential energy
Fig.
1. Lifting the object vertically
produces an increase in the gravitational potential energy of the System comprising
the object and the Earth.
Work done by hand = Increase in gravitational potential energy (2)
Near the Earths surface: g = constant (positive number) g = 9.81 m.s-2 The gravitational potential energy
represents an energy stored
by the object in the gravitational field surrounding the Earth. For example,
if the object is released by the hand and then falls a vertical distance h. The loss in potential energy is
equal to the gain in the objects kinetic energy. Loss
in potential energy = Gain in kinetic energy (3) Hence, one can predict the velocity v of the object starting with an
initial velocity u when it has fallen a distance h. Equation 2 and 3 are only applicable
near the Earths surface where the
value of the gravitational field strength g (acceleration due to gravity) is a
constant. To find a more general expression for the gravitational potential
energy, you must consider how the gravitational force varies with distance
from the centre of the Earth. Consider the application of an
external force F which moves an object of mass m at a constant velocity from its
initial position a distance r from
the centre of the Earth to an infinite distance away from the Earth. The work
done W on the object by the force F increases the gravitational
potential energy Since the object moves away from the
Earth at a constant speed (a = 0), the magnitudes of the applied
force F and
the gravitational force FG are equal (|
F
| = | FG |)
Therefore, we can define the gravitational potential energy at a point
which is a distance r from the centre of the Earth as (4) Figure 2 shows the variation in the
gravitational force as a function of distance (Newtons Law of Universal
Gravitation). This is an inverse square law. When r = 1.0 a.u., what is the value of F ? When r is doubled, r = 2.0 a.u., what is the value
of F ? Explain why your values agree with the predictions of the
inverse square law.
Fig. 2. The gravitational
force as a function of distance from the centre of the Earth in arbitrary
units. Figure 3 shows the variation in
gravitational potential energy When r = 1.0 a.u., what is the value of EP ? When r is doubled, r = 2.0 a.u., what is the value
of EP
? Explain why your values agree with the predictions of the
inverse proportionality relationship.
Fig. 3. The gravitational
potential energy as a function of distance from the centre of the Earth in
arbitrary units. It is not meaningful to talk about
the gravitational potential energy possessed by an object. It is best to
refer to the potential energy of a system and define a reference point where
the potential energy is taken as zero. The change in
potential energy is a more important quantity than the actual value of the
potential energy. |
|
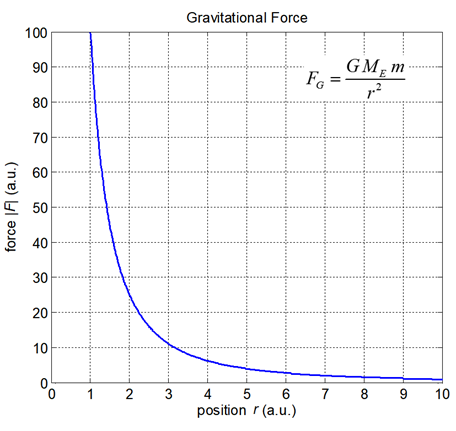
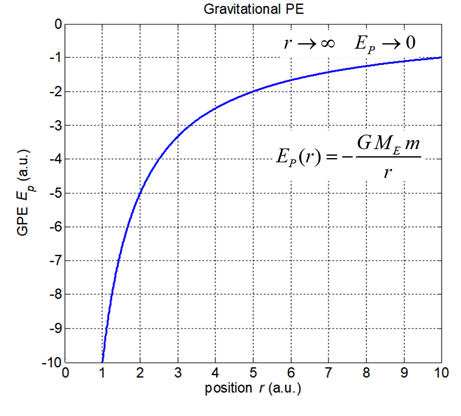
Exercise using Figure 3 How much energy (work) is required
by an applied force to move an object of mass m from r = 1.0 a.u.
to r = 5.0 a.u. r = 1.0 a.u.
to r = An object is released from rest at a
point where r = 5.0 a.u.
Describe the subsequent motion of the object. When r = 1.0 a.u.,
what will be the value of its kinetic energy? How would the values change if the
mass of the object was 2m ? |
|
Conservation of energy Consider an object in motion that is
acted upon only by the gravitational force. Then in the system of the Earth
and the object, the total energy of the system is conserved. Hence, as the
object moves, the change in total energy is zero. Kinetic
energy of the object, EK Gravitational
potential energy of system (GPE), EP Total
energy of system, E
= EK + EP gain
in KE = loss in GPE or loss in KE = gain in GPE |
|
Consider the flight of a cricket
ball in the air. In flight the ball is only acted upon by the gravitational
force. The ball initially has its maximum value for its KE and a minimum
value for GPE. As the ball rises its potential energy increases at the same
rate as its kinetic energy decreases. When the ball reaches its maximum
height, its potential energy is a maximum and its kinetic energy a minimum
(KE = 0). As the fall falls its potential energy decreases at the same rate
as its kinetic energy increases. gain in KE = loss in
GPE or loss in KE = gain in GPE Consider a cricket ball dropped from
a tower. The ball falls vertically a distance of 134 m from rest before
hitting the ground. What is the velocity of the ball immediately before
hitting the ground? Solution How to
approach the problem (Identify
Setup Execute Evaluate) Draw an
annotated diagram Type of
problem: conservation of energy Knowledge: total energy E = EK + EP = constant gain in KE = loss in
GPE or loss in KE = gain in GPE
Total
energy E
= E1 = E2 EK1
+ EP1 = EK2
+ EP2 0 + mgh1
= mv22
+ 0 v2 = + 51 m.s-1 |
|
To visualise how energy is stored, watch
the animation of a vibrating object attached to a spring. The total energy of
the system remains constant but the there is a continual transfer between the
stored energy of the spring (elastic potential energy) and the kinetic energy
of the oscillating object.
|
|
Ian Cooper School of Physics University of Sydney If you have any feedback, comments,
suggestions or corrections please email Ian Cooper ian.cooper@sydney.edu.au |