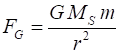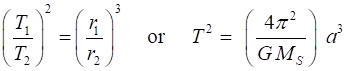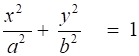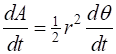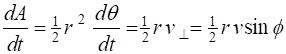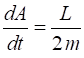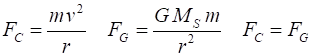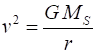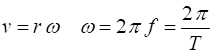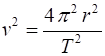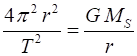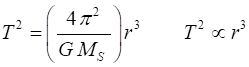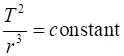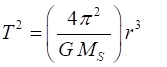MODULE 5
ADVANCED MECHANICS
KEPLERS LAWS AND THE
MOTION OF PLANETS
|
How do the planets
move ? Keplers Laws of Motion One of the most important questions
historically in Physics was how the planets move. Many historians consider the field of
Physics to date from the work of Newton, and the motion of the planets was
the main problem Newton set out to solve.
In the process of doing this, he not only introduced his laws of
motion and discovered the law of gravity, he also
developed differential and integral calculus. Today, the same laws that govern the motion
of planets, are used by scientists to put satellites
into orbit around the Earth and to send spacecraft through the solar system. How the planets move is determined by
gravitational forces. The forces of
gravity are the only forces applied to the planets. The gravitational forces between the
planets are very small compared with the force due to the Sun since the mass
of the planets are much less than the Sun's mass. Each planet moves almost
the way the gravitational force of the Sun alone dictates, as though the
other planets did not exist. The motion of a planet is governed by Newtons Law of Universal Gravitation (1) where G is the
Universal Gravitational Constant, MS is the mass
of the Sun, m is the mass
of the planet and r
is the
distance from the Sun to the planet. G = 6.6710-11 N.m2.kg2 MS = 2.01030 kg Historically,
the laws of planetary motion were discovered by the outstanding German
astronomer Johannes Kepler (1571-1630) based on almost 20 years of processing
astronomical data, before Newton and without the aid of the law of
gravitation. Kepler's Laws of
Planetary Motion 1.
The
path of each planet around the Sun is an ellipse
with the Sun at one focus. 2.
Each
planet moves so that all imaginary lines drawn from the Sun to the planet
sweeps out equal areas in equal periods of
time. 3.
The
ratio of the squares of the periods T2
of revolution of the planets is equal to the ratio of the cubes of their
orbital radii r3 (mean
distance from the Sun or length of semi-major axis,
a) (6) Keplers First Law
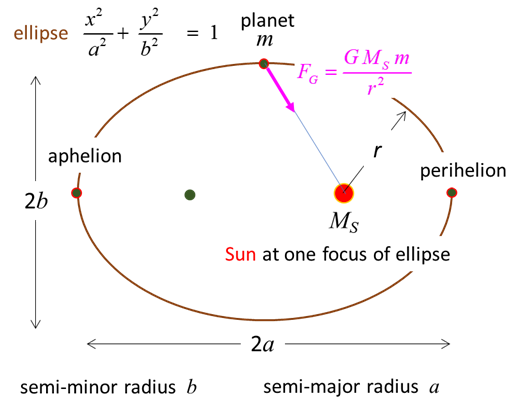
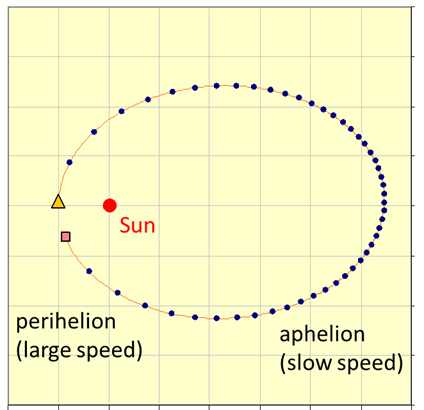
A planet describes
an ellipse with the Sun at one focus. But what kind of an ellipse do planets
describe? It turns out they are very close to circles. The path of the planet
nearest the Sun, Mercury, differs most from a circle, but even in this case,
the longest diameter is only 2% greater than the shortest one. Bodies other
than the planets, for example, comets move around the Sun in greatly
flattened ellipses. Since the Sun is located at one of the foci
and not the centre, the distance from the planet to the Sun changes as the
planet moves in its orbit.. The point nearest the
Sun is called the perihelion
and the farthest point from the Sun is the aphelion. Half the distance from the perihelion to the
aphelion is known as the semi-major radius
a. The other
radius of the ellipse is the semi-minor radius
b. The equation of an ellipse is (7)
Fig. 1.
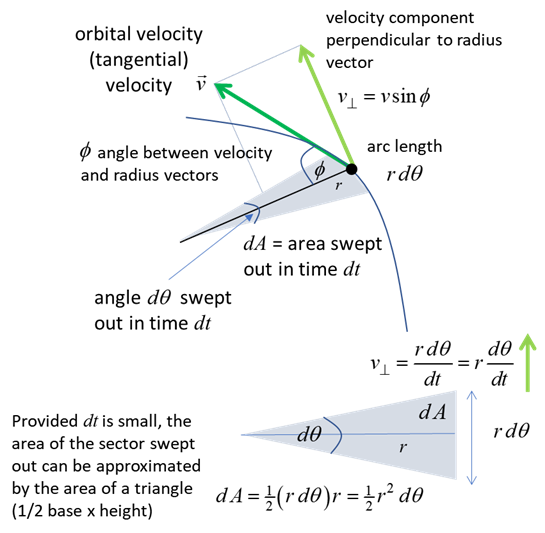
The path of a planet around the Sun is an ellipse. Kepler's Second Law
Each planet moves
so that an imaginary line drawn from the Sun to the planet sweeps out equal
areas in equal periods of time. In a small
time interval
Therefore,
the area of the sector swept out can be approximated as the area of a
triangle given by The area When the
planet is close to the Sun, r is small and
Fig. 2. A planet moves
so that an imaginary line drawn from the Sun to the planet sweeps out equal
areas in equal periods of time. Keplers Second law follows from
Newtons laws. The component of the orbital velocity Combining gives The magnitude
of the angular momentum is Hence, No external
torques act on the system, hence, the angular momentum L must be a constant
(law of conservation of angular momentum) and this
means that the area swept out per unit time is also a constant, which is
simply Keplers 2nd law. "Equal
areas in equal times" means the rate at which area is swept out on the
orbit Kepler's Third Law
For a planet orbiting the Sun with a radius
r, the
centripetal force results from the gravitational attraction between the planet
and the Sun Centripetal
force = Gravitational force
For
rotational motion, we know that
|
|
Exercise 1 Where is Mars? One year on Mars (time for one
complete orbit around the Sun) is 687 Earth days. Determine the distance of
Mars from the Sun. RSE = 1.50x1011 m Solution We can use Keplers 3rd Law Earth (1) T1 = TE = 365 days
r1 = RSE = 1.50x1011 m Mars (2) T2 = TM = 687 days
r2 = RSM = ? m |
|
Exercise 2 How can we determine the mass of the Sun if we know the distance
between the Sun and the Earth? Solution We can use Keplers 3rd Law G = 6.67x10-11 N.m2.kg-2
T = TE = 1 y = (1)(365)(24)(3600) s = 3.17x107 s r = RSE = 1.50x1011 m
|
|
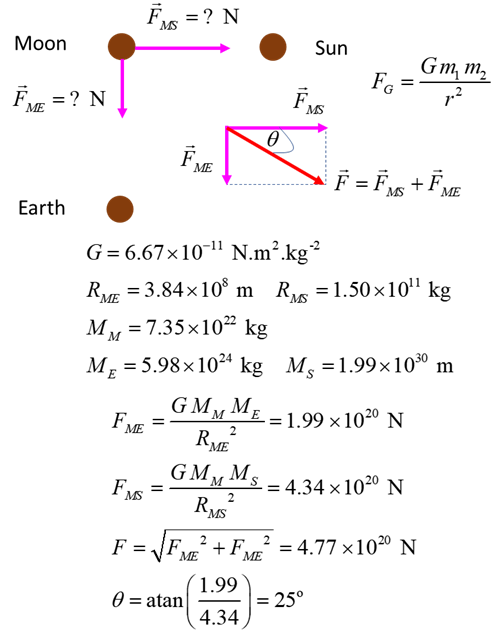
Exercise 3 Gravitational Force
on the Moon The Moon, the Sun and the Earth are aligned so that both the Sun
and the Earth are at right angles to each other. Find the net force acting on
the Moon.
Solution THINK: how to approach the problem (ISEE) / type of problem /
visualize the physical situation / annotated scientific diagram / what do I
know! Need to calculate the forces between the Moon and Earth and
between Moon and Sun and then add the two forces as vectors.
|
|
Ian Cooper School of Physics University of Sydney If you have any feedback, comments,
suggestions or corrections please email Ian Cooper ian.cooper@sydney.edu.au |