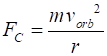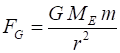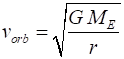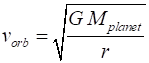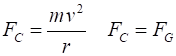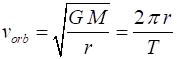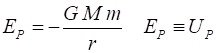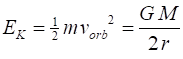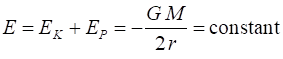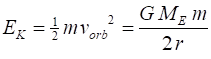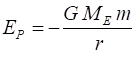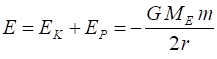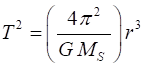MODULE 5
ADVANCED MECHANICS
MOTION OF SATELLITES
|
A satellite is an object that orbits a much more massive
object. Natural satellites include
the planets orbiting the Sun, the moons of Jupiter, and the Moon about the
Earth. An artificial satellite is an
object put into orbit from
the Earths surface using a spacecraft such a rocket or a space shuttle.
Satellites are used for many applications and include military and civilian
Earth observation satellites, communications satellites, navigation
satellites, weather satellites, and research satellites. Space stations and
human spacecraft in orbit are also satellites.
Satellites
are placed in one of several different types of orbit depending on the nature
of their mission. Two common orbit
types are a Low Earth Orbit (LEO) and a Geostationary Orbit (GEO).
Low Earth Orbit (LEO) occur at a radius
of between 200 and 2000 km above the Earths surface with periods varying
from 60 to 90 minutes. The space
shuttle uses this type of orbit (200-250 km).
LEOs have the smallest field of view and frequent coverage of specific
or varied locations on the Earths surface. Orbits less than 400 km are
difficult to maintain due to atmospheric drag and subsequent orbital decay. They are used mainly for military
applications, Earth observation, weather monitoring and shuttle missions.
Except for the lunar flights of the Apollo program, all human spaceflights
have taken place in LEO. The altitude record for a human spaceflight in LEO
was Gemini 11 with an apogee of 1,374 km. All manned space stations and most
artificial satellites, have been in LEO. Orbital decay is
the reduction in the height of an object's orbit over time due to the drag of
the atmosphere on the object. All satellites in low Earth orbits are subject
to some degree of atmospheric drag that will eventually decay their orbit and
limit their lifetimes. Even at 1000 km, as thin as the atmosphere is, it is
still sufficiently dense to slow the satellite down gradually. A Geostationary Orbit (GEO) is a circular orbit in
the Earth's equatorial plane, any point on which revolves about the Earth in
the same direction and with the same period as the Earth's rotation.
Geostationary orbits are useful because they cause a satellite to appear
stationary with respect to a fixed point on the rotating Earth. As a result,
an antenna can point in a fixed direction and maintain a link with the
satellite. The satellite orbits in the direction of the Earth's rotation, at
an altitude of approximately 35,786 km above ground. This altitude is
significant because it produces an orbital period equal to the Earth's period
of rotation, known as the sidereal day.
These orbits allow for the tracking of stationary points on Earth and have
the largest field of view. Applications include communications, mass-media
and weather monitoring. Web
investigation
artificial satellite orbits http://en.wikipedia.org/wiki/Satellite http://en.wikipedia.org/wiki/Low_Earth_orbit http://en.wikipedia.org/wiki/Geostationary_orbit CIRCULAR ORBITAL
MOTION We will
assume that a satellite moves in a circular path
around the Earth. To place an object into a stable Earth orbit at a given
radius, the launch must give it both an initial vertical and horizontal
component of velocity, relative to the Earths surface. The rocket will
eventually turn so that it is travelling horizontal to the Earths surface.
At this radius, the force of gravity provides the acceleration needed to keep
the object moving in a circle, but a particular orbital velocity is also
required to keep the object in a stable orbit (figure 2). To calculate that
velocity, known as the orbital velocity Orbital velocity of a satellite around orbiting the Earth in a
circular path (1) Note that the
velocity of a satellite as it orbits around the Earth in a circle only
depends on: Mass of the Earth Radius of the orbit
It is clear
from this formula that altitude is the only variable that determines the
orbital velocity required for a specific orbit. Further, the greater the
radius of that orbit, the lower that orbital velocity The orbital
velocity of a satellite around other planets is simply (4) The orbital motion
of the Moon about the Earth We can calculate the orbital velocity The Moons orbital velocity of was
calculated to be 1.02 km.s-1. The Moons orbit is not quite
circular and the speed is only approximately constant. The orbital speed of the of the Moon varies from 0.970 to 1.022 km.s-1.
So, our simple models gave numerical results which compare very favourably
with the measured values for the orbital speed of the Moon.
|
|
ENERGY CONSIDERATIONS Consider
a satellite of mass m orbiting a
massive object of mass M (m << M assume M
stationary w.r.t m) with an
average orbital radius r, orbital
speed The net force
acting on the satellite is the gravitational force The
gravitational force is responsible for the orbit, thus the gravitational
force corresponds to the centripetal force Hence the average orbital speed is The
gravitational potential of the satellite system is and its
kinetic energy is The total
energy of the system is Conservation
of energy For a satellite in a circular orbit, the
radius of orbit and the orbital velocity (tangential) are both constants. In
an elliptical orbit, both the radius and orbital velocity change during the
orbit of the satellite. However, the angular momentum L of the satellite remains constant So, if the radius increases, the orbital velocity
decreases or if the radius decreases, then the orbital velocity increases. By
carefully examining figure 5, you will observe that when the satellite is at
the aphelion position, the satellite is at the greatest distance from the
massive object and its speed is a minimum. When the satellite is at the
perihelion position, the position closest to the massive object and smallest
radius, the speed is a maximum. |
|
Exercise 1 A satellite of mass 2500 kg is in a low orbit
trajectory at an altitude of 1000 km above the Earths surface. The satellite
must be moved to a higher trajectory with an altitude of 2000 m. Calculate for both orbits: the acceleration
due to gravity (gravitational field strength), orbital speeds, periods,
kinetic energies, gravitational potential energies and total energies. How can this be achieved? What energy must be used to shift the
satellite into the higher orbit?
Solution Problem: type / visualize / how to
approach ? / scientific
annotated diagram / what do you know ?
Acceleration due to gravity (gravitational
field strength)
Orbit #1
g = 7.33 m.s-2 Orbit #2 g
= 5.69 m.s-2 Orbital velocity decreases with increasing
altitude. The period of the satellite orbits
Orbit #1
T = 6.30x103 s = 1.75
h Orbit #2
Period increases with increasing altitude. Kinetic energies of the satellite
Orbit #1
Orbit #2 KE decreases with increasing altitude. Gravitational potential energies of the
satellite
Orbit #1
Orbit #2 GPE increases with increasing altitude. Total energies of the satellite
Orbit #1
Orbit #2 total energy
increases with increasing altitude. The total energy
being negative means that the satellite is bound to the Earth. The energy (work) required to move the
satellite from orbit #1 to orbit #2 is the difference in the total energies
between the two orbits
work W = E2 E1 = ( - 5.95x1010
+ 6.76x1010 ) J
W = 0.81x1010 J This energy for the work required to shift
the orbit must come from the fuel that is burnt by the satellites rockets.
|
|
Exercise 2 How can we determine the mass of the Sun if we know the distance
between the Sun and the Earth? Solution We can use Keplers 3rd Law G = 6.67x10-11 N.m2.kg-2
T = TE = 1 y = (1)(365)(24)(3600) s = 3.17x107 s r = RSE = 1.50x1011 m
|
|
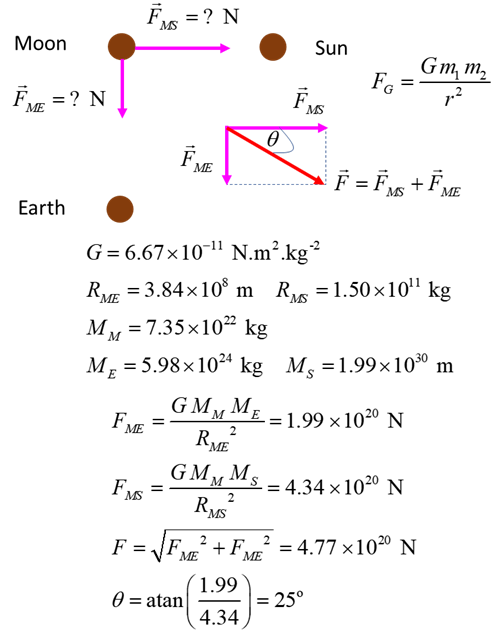
Exercise 3 Gravitational Force on the Moon The Moon, the Sun and the Earth are aligned so that both the Sun
and the Earth are at right angles to each other. Find the net force acting on
the Moon.
Solution THINK: how to approach the problem (ISEE) / type of problem /
visualize the physical situation / annotated scientific diagram / what do I
know! Need to calculate the forces between the Moon and Earth and
between Moon and Sun and then add the two forces as vectors.
|
|
Ian Cooper School of Physics University of Sydney If you have any feedback, comments,
suggestions or corrections please email Ian Cooper ian.cooper@sydney.edu.au |