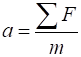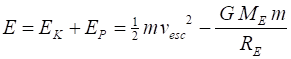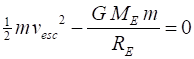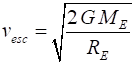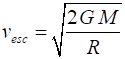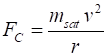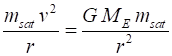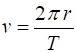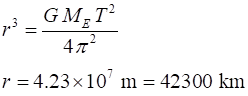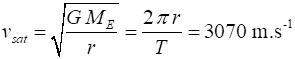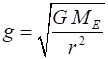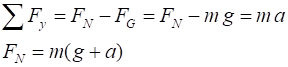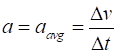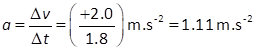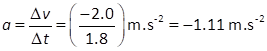MODULE 5
ADVANCED MECHANICS
MOTION OF SATELLITES
AND ROCKETS
|
PUTTING SATELLITES INTO ORBIT The
greater the launch velocity of an object, the greater the vertical height
reached and the greater the horizontal range. If the launch velocity is
greater enough then the acceleration due to gravity is no longer constant and
we must use its dependence on the distance of the object from the centre of
the Earth. Also, if the launch velocity is large enough, the object can be
placed into orbit around the Earth or escape from the influence of the
Earths gravitation field. Rockets
and satellites are essential devices for our modern world based upon the
internet, GPS and mobile phones. Communications around the globe between
mobile phones, computers, etc use radio waves and
microwaves for the transfer of information. Satellites are used for: radio
and television transmissions; weather; military applications; GPS; phones and
more. Just about all parts of the globe can transmit or receive
electromagnetic wave communications via orbiting satellites and Earth bound
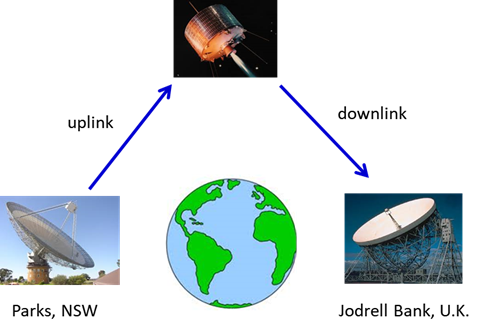
transmitters and receivers (figure 1).
Fig. 1. Radio telescopes and satellites make it
possible for information to flow freely around the globe. There are 24 satellites that make up
the GPS space segment. They orbit the Earth about 20000 km above us. These
satellites are travelling at speeds of approximately 11 000 km.h-1
and make two complete orbits in less than 24 hours. GPS satellites are powered
by solar energy. They have backup batteries on-board to keep them running in
the event of no solar power. Small rocket boosters on each satellite keep
them flying in the correct path. GPS satellites transmit two low power radio
signals, designated L1 and L2. Civilian GPS use the L1 frequency of 1575.42 MHz in the UHF band. The signals travel by line of sight,
meaning they will pass through clouds, glass and plastic but will not go
through most solid objects such as buildings and mountains. LAUNCHING A ROCKET
A rocket is propelled through space
by a continuous explosion produced by burning fuel and expelling the
resulting hot gases out one end. Chemical reactions take place inside the
rocket and the gaseous products of combustion are propelled out of the rocket
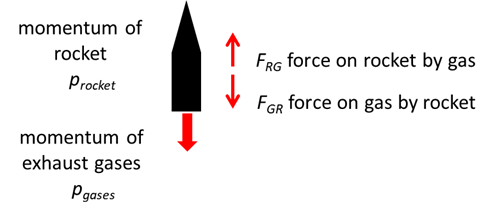
with tremendous a force acting on the gas. The hot gases have a momentum in
one direction, and since the total momentum of the rocket-fuel system is
zero, the rocket itself has an equal momentum in the opposite direction.
Thus, the rocket moves off in the opposite direction to the expelled gases,
in accordance with the Law of Conservation of Momentum. This means that the backward
momentum of the gases is exactly equal in magnitude to the forward momentum
of the rocket. This is what gives the rocket its forward velocity. This is a consequence of Newton's Third Law
which says that for every reaction there is an equal and opposite reaction;
the rocket exerts a force on the gases and the gases exert a force on the rocket
propelling it forward. This propulsive force is referred to as the thrust of the rocket.
Fig.
2. Rocket propulsion. Newtons third law: Forces act for time interval impulse: Impulse = Change in momentum:
Momentum is conserved: You should note that because at any
time instant the mass of the gases is much less than the mass of the rocket,
we can see that the velocity of the gases will, therefore, be much higher in
magnitude than the velocity of the rocket. Although the mass of the gas
emitted per second is comparatively small, it has a very large momentum
because of its high velocity. An equal momentum is imparted to the rocket in
the opposite direction. This means that the rocket, despite its large mass,
builds up a high velocity. As the launch proceeds, fuel is
burnt, gases expelled and the mass of the rocket decreases. This produces an increase in acceleration,
since acceleration is proportional to the applied force (the thrust) and
inversely proportional to the mass.
The initial acceleration is small, around 1 m.s-2 but
continues to build as the mass of the rocket decreases. Rockets
acceleration not constant: initially 90% mass
of rocket is its fuel fuel used up mass of rocket decreases thrust
remains approximately constant acceleration increases as mass
reduces An additional positive effect on the
rocket is the decreases in aero dynamic drag with increasing altitude. The combination
of these two factors accounts for the increase in acceleration during the
launch of the rocket and helps the spacecraft reach the high velocity that is
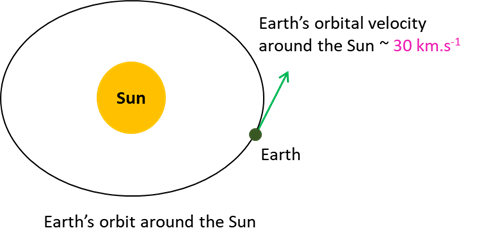
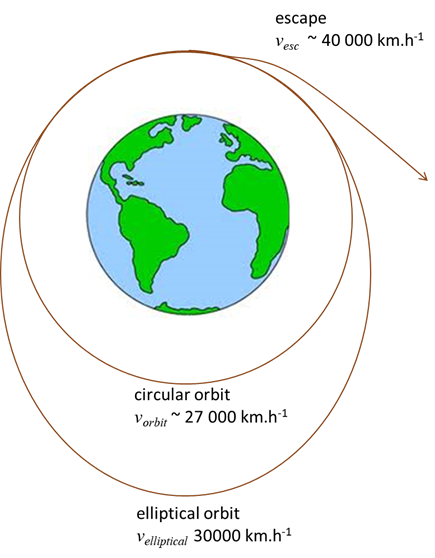
needed for space flight. ESCAPE VELOCITY For a spacecraft to go on a mission
to another planet, it is first necessary for the spacecraft to achieve escape
velocity from the Earth and to go into its own elliptical orbit around the
Sun. The Earth orbits the Sun at about 30 km.s-1. Again, it makes good sense to use this
speed to help a spacecraft achieve escape velocity for trips to other
planets. So, if the spacecraft is to
go on a mission to planets beyond the Earths orbit, it is launched in the
direction of Earths orbital motion around the Sun and achieves a velocity
around the Sun greater than the Earths 30 km.s-1. Thus, the spacecrafts orbit is larger than
that of the Earth and is arranged to intersect with the orbit of the planet
to which it is heading at a time when the planet will be at that point. Similarly, if the target is Mercury or
Venus, the spacecraft is launched in the opposite direction to the Earths
motion through space. Then, the
spacecraft achieves an escape velocity less than 30 km.s-1, where
it enters an elliptical orbit around the Sun that is smaller than the Earths
and can thus intercept either planet.
Fig. 3. Earths orbital motion around the Sun can
be helpful in launching rockets to planets in our Solar System. Newton showed that if you climb to
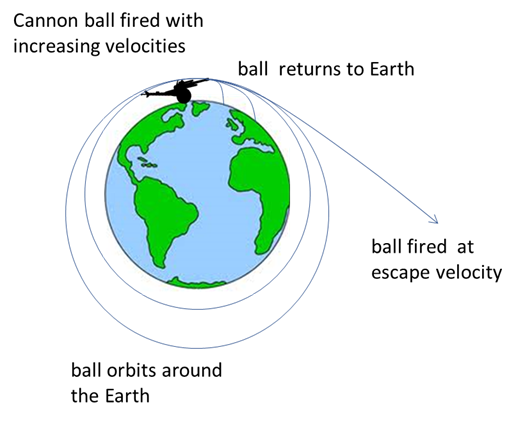
the top of a mountain and throw a ball, it will travel a certain distance and
then hit the ground (A). If you could throw the ball twice as fast it would
travel even further (B) and if you threw it three times as fast it would
travel further still. If you kept increasing the speed by firing it from a
super powerful canon, and there was no air friction, a point would come when
the ball would be travelling part-way around the world. If the ball could be
fired at just the right speed, it would travel completely around the Earth
and hit you in the back of the head (C). In this case, it would fall at
exactly the same rate as the Earth curves. Faster still, the ball would go
into elliptical orbit (D). If it was fired much faster than that, the canon
ball would travel off into space and never return (F) as shown in figure 4.
Fig. 4 Cannon ball launched from top of a
mountain with increasing velocity. Escape velocity For a rocket of mass m fired from the surface of the
Earth, the total energy of the rocket-Earth system is assumed to be constant.
At the Earths surface, the total
energy when the rocket is fired is When the rocket has escaped the
Earths gravitational pull, we assume the rocket is an infinite distance from
the Earth Total energy is conserved Therefore, the escape velocity is (1) The escape velocity for a rocket
fired from a planet or moon (mass M, radius R) is (2) Note that the mass m of the object has cancelled, so
that the escape velocity of any object is independent of its mass. This means
that if you want to throw a grain of rice or an elephant into outer space,
you need to give them both the same initial velocity which for the Earth
works out to be about 104 m.s-1.
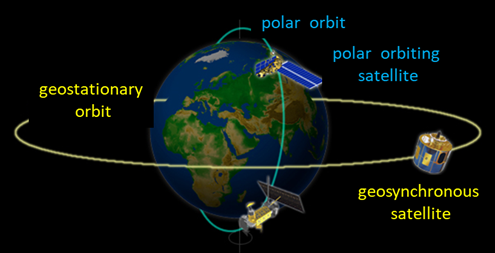
Geosynchronous (geostationary) satellite A geosynchronous satellite is one that stays above the same
point on the Earth, which is possible only if it is above a point on the
equator. Such satellites are used for weather forecasting, TV transmissions,
and communication relays.
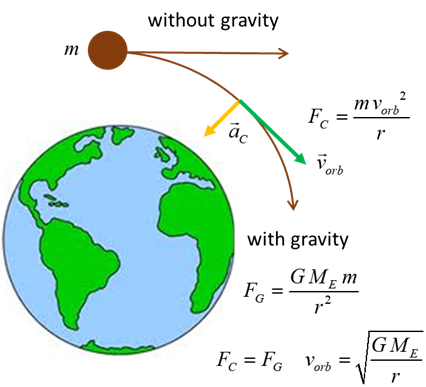
The only force acting on the satellite is the gravitational
force. So, for the orbiting satellite, the gravitational force must be equal
to the centripetal force assuming that the satellite moves in a circle
This equation has two unknowns Thus, the speed of the satellite must be where We can now solve for r and v The radius of the Earth is So, a geosynchronous satellite must orbit
at a distance of about 36 000 km above the
surface of the Earth. The orbital speed |
|
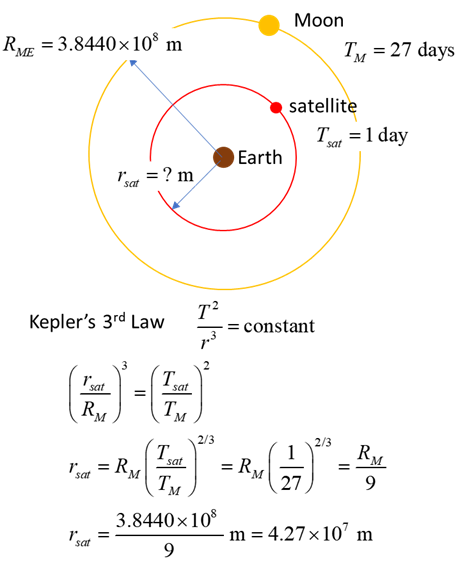
Example 1 For the radius for the orbit of a
geosynchronous satellite given that the distance between the Earth and the
Moon is 384 400 km. Solution THINK: how to approach the
problem / type of problem / visualize the physical situation / annotated
scientific diagram / what do I know!
How nice that the moons approximate period turns out to be a perfect cube! A geosynchronous satellite must be 1/9 the distance to the Moon (42 000 km from the centre of the Earth or 36 000 km above the Earths surface which equals about 6 Earth radii high). |
|
SATELLITES and WEIGHTLESSNESS Artificial satellites circling the Earth
are common. A satellite is placed into orbit by accelerating it to
sufficiently high tangential speed with the use of rockets. If the speed is
too low, it will return to the Earth. If the speed is too high, the
spacecraft will not be confined by the Earths gravity and will escape, never
to return. Satellites are usually placed into circular (or nearly circular)
orbits because this requires the least take-off speed (figure 5).
Fig. 5. Artificial satellites launched
with different speeds. What keeps the satellite up?
Fig. 6. A moving
satellite is always falling towards the centre of the Earth. A satellite is always falling towards the Earth,
i.e., accelerating towards the Earth by the pull of the gravitational force.
The high tangential speed keeps the satellite from hitting the Earth as the
curvature of the satellites orbit as it falls matches the curvature of the
Earth. The weightlessness
experience by astronauts in a satellite orbit is because they are falling
freely since the satellite is falling freely towards the Earth. The
acceleration of the satellite and astronauts matches the acceleration due to
gravity at that point since the only force acting is the gravitational force
of the Earth Figure 7 shows
examples of people in free-fall and experience the sensation of
weightlessness.
Fig.
7. Weightlessness on Earth. Weightlessness
does not mean your weight is zero. Your weight is still given by the
gravitational force weight
Fig. 8. The weight of the person is both cases in equal to |
|
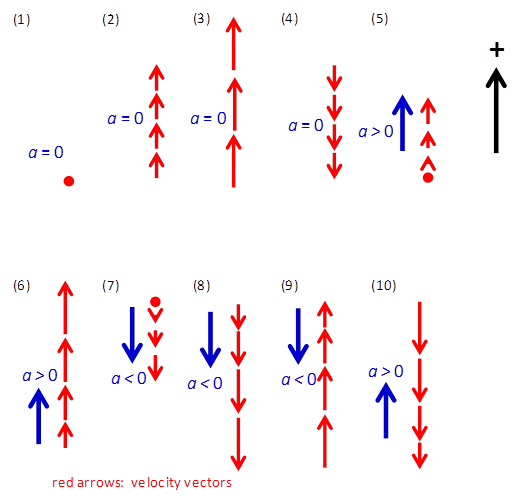
Example 2 A 60 kg person stands on a bathroom scale while riding an elevator.
What is the reading on the scale in the following cases: (1)
The
elevator is at rest. (2)
The
elevator is going up at 2.0 m.s-1. (3)
The
elevator is going up at 4.0 m.s-1. (4)
The
elevator is going down at 2.0 m.s-1. (5)
The elevator
starts from rest and goes up reaching a speed of
2.0 m.s-1 in 1.8 s. (6)
The
elevator is moving up and accelerates from 2.0 m.s-1
to 4.0 m.s-1 in 1.8 s. (7)
The
elevator starts from rest and goes down reaching a speed of
2.0 m.s-1 in 1.8 s. (8)
The
elevator is moving down and accelerates from 2.0 m.s-1
to 4.0 m.s-1 in 1.8 s. (9)
The
elevator is moving up and slows from 4.0 m.s-1
to 2.0 m.s-1 in 1.8 s. (10)
The
elevator is moving down and slows from 4.0 m.s-1
to 2.0 m.s-1 in 1.8 s. Solution THINK: how to approach
the problem / type of problem / visualize the physical situation / annotated
scientific diagram / what do I know! Visualize
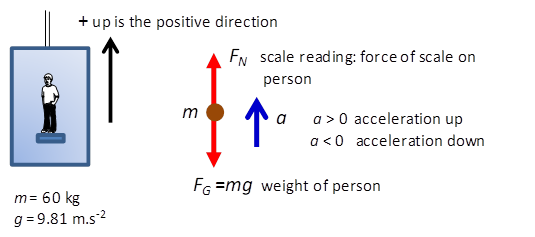
the situation write down all the given and unknown information. Draw a
diagram of the physical situation showing the inertial frame of reference.
Type of problem forces and
Newtons laws.
Draw a free-body diagram showing
all the forces acting on the person.
Use Newtons 2nd law to
give the relationship between the forces acting on the person and the
acceleration of the person.
Determine the acceleration of the
person in each case.
Solve for the unknown quantities.
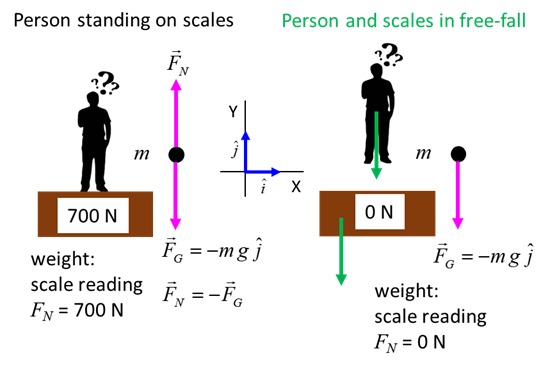
The person exerts a force on the bathroom scales and the bathroom
scales exerts a force on the person. This is an action / reaction pair. But,
we are only interested in the forces acting on the person which are the
weight and the normal force due to the scale on the person. The scale reading FN
is found from Newtons 2nd law: acceleration due to gravity g
= 9.8 m.s-2 (scalar
quantity in this example) acceleration of person a
> 0 if direction up and a < 0
if acceleration down The weight of the person is
FG = mg = (60)(9.81) N =588.6 N We can assume when the velocity changes the acceleration a is constant and equal to the average
acceleration In cases (1), (2), (3) and (4) there is no change in the
velocity, hence Therefore, the scale reading is FN = 588.6 N or 60 kg. For cases (5), (6) and (10)
case
(5) case (6)
case (10) The acceleration is The scale reading is This scale reading is often called the persons apparent weight. The person feels the floor pushing
up harder than when the elevator is stationary or moving with a constant
velocity. For cases (7), (8) and (9)
case
(7) case (8)
case (9) The acceleration is The scale reading is The person feels their weight has
decreased. In the extreme case when the cable
breaks and the elevator and the person are in free-fall and the downward
acceleration is a = -g. In this case the normal force of
the scales on the person is FN
= m(g - g) = 0 N. The person seems to be weightless. This is the same as
an astronaut orbiting the Earth in a spacecraft where they experience apparent weightlessness. The astronaut and spacecraft
are in free-fall and there are zero normal forces acting on the person. The
astronaut still has weight because of the gravitational force acting on them. The acceleration does not depend
upon the direction of the velocity. What is important is the change in the velocity. A good way to understand this concept is to
draw the appropriate motion maps
|
|
Ian Cooper School of Physics University of Sydney If you have any feedback, comments,
suggestions or corrections please email Ian Cooper ian.cooper@sydney.edu.au |