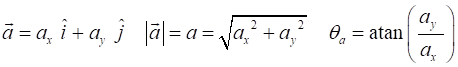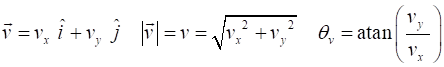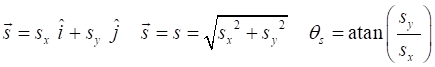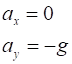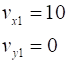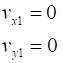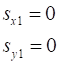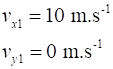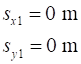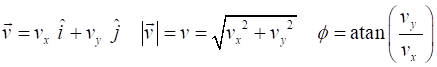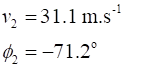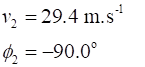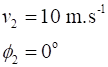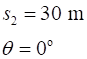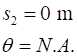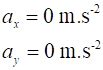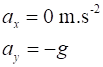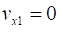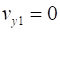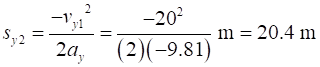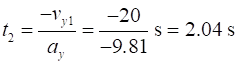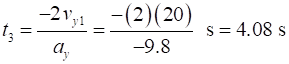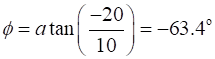MODULE 5
ADVANCED MECHANICS
[2D] MOTION IN A PLANE
|
We will consider the two-dimension motion of objects moving in a
plane with a uniform
acceleration. Again, the first step is define a frame of reference
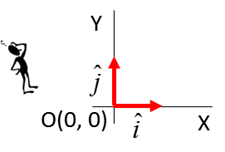
Origin
O(0,0, 0) reference point Cartesian coordinate axes (X, Y, Z) Unit vectors Specify
the units The equations for the [2D] motion
of an object moving in a plane are acceleration velocity displacement These vectors equations are not
very useful. It is much better to express the equation for [2D] motion in
terms of the X and Y components of each vector. Remember a vector component
is a scalar quantity. When the object is moving with a uniform (constant) acceleration, the equations
describing the motion for the time interval t
between Event #1 (initial values) and Event #2 (final values) are time acceleration velocity displacement vectors
The
angles
N.B. subscripts 1 and 2 denote the time for Event #1 and Event #2
and We
will consider the [2D] motion in a plane called projectile motion. When studying Physics, one key to
becoming successful is being able to visualize a physical phenomenon. So,
make an effort to visualize the flight of a thrown ball, a golf ball and a
tennis ball.
Now
Physics is not about the real-world. A Physicist looks at a physical
phenomenon and makes a set of approximations
and simplifications
to develop a mathematical model that can be used to make predictions. These predictions are then compared to
the real-world measurements to test the validity of the mathematical model.
The simple model is often expanded by adding complexities to given a better
model of the real-world situation. In
developing our model of the flight of a ball, we need to make lots of
approximations and simplifications. The ball is identified as our system
(point particle) and is represented as a dot in a scientific diagram. We
ignore the action of throwing or catching the ball and ignore any contacts
with an obstacle e.g. our ball does not hit the ground. We are only
interested in the flight of the
ball. Assume that the ball only moves in a vertical plane and ignore any
friction effects or effects of the wind.
The
acceleration is assumed to be constant (does not change with time) such that
Event
#1 gives the initial values for the time, velocity and displacement of our system
and Event # 2 gives the final values for time, velocity and displacement. Exercise
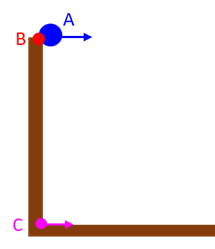
System A 10 kg
blue
ball System B 5 kg
red
ball System C 1 kg
magenta
ball Event #1 ( The three balls are launched simultaneously as shown in the diagram and the initial values are displayed in the table. |
|
|
A |
B |
C |
|
mass [kg] |
|
|
|
|
time [s] |
|
|
|
|
acceleration [m.s-2] |
|
|
|
|
velocity [m.s-1] |
|
|
|
|
displacement [m] |
|
|
|
|
acceleration due to gravity [m.s-2] |
|
|
|
|
Event #2 ( The time interval for the motion
of the balls is 3.0 s. A. Visualize the motion of the three balls.
On a single diagram, sketch for the trajectory for each ball. B. What the final values for the
acceleration, velocity and displacement after 3.0 s? Give the values for the components,
magnitudes and directions. C. For each ball, draw a series of graphs to
show the variation with time in the 3.0 s interval for: the trajectories;
acceleration components; velocity components and displacement components. D. What can you
conclude about the independence of the motions in the horizontal (X) and
vertical (Y) directions? Only
after you have completed Part (A), view an animation of the projectile motion
of the three balls below. How do your predictions agree with the trajectories
displayed in the simulation? |
|
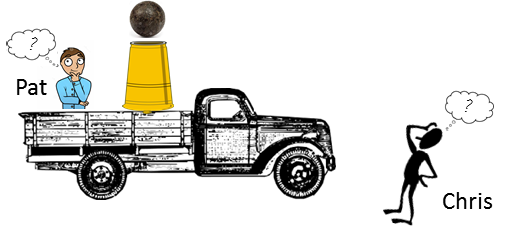
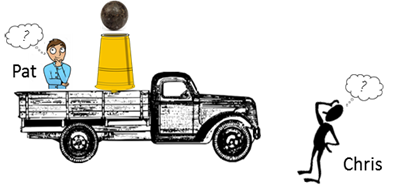
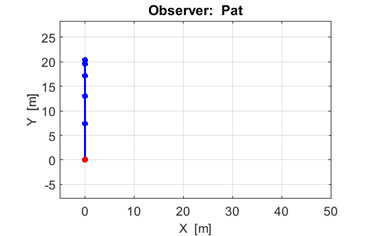
Animation Two people are observing a truck carrying a cannon. The truck is travelling at 10 m.s-1
when a cannon
ball is fired vertically into the air. The ball leaves the cannon at 20 m.s-1. One observer, Pat is sitting on the back of
the truck with the cannon and Chris
is standing on the ground watching the truck and cannon. Below is an animation of the flight of the cannon ball and the motion of the truck from Pats frame of reference and
from Chriss
frame of reference. |
|
|
|
|
|
Fig.
1. The motion of the truck
and cannon
ball from Pats frame of reference. |
|
|
|
Fig.
2. The motion of the truck
and cannon
ball from Chriss frame of reference. |
|
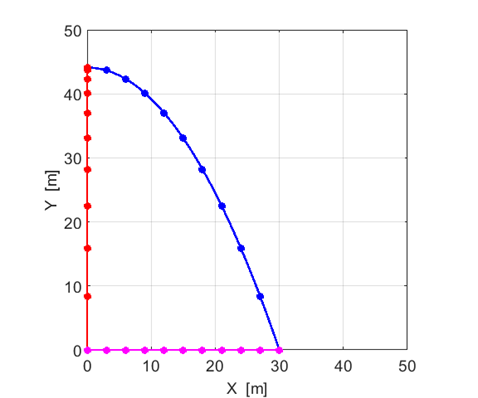
Figure 3 shows the trajectories of the three particles: System A 10 kg blue ball System B 5 kg red ball System C 1 kg magenta ball The solid curves show the paths for the three balls. The coloured
dots show the positions of the balls at 0.30 s intervals.
Fig. 3.
The trajectories of the three balls. The blue
(A) and red (B) balls have identical vertical motions. The blue
(A) and magenta (C) balls have
identical horizontal motions. The horizontal motion and vertical motion are independent of each other. The motion of a ball does not depend upon its mass. Figure 4 show the variation in the components of the acceleration,
velocity and displacements as functions of time. The colour of the line
identifies the ball (A blue, B red, C magenta). If two or more of the results
for the graph are the same, the colour is shown as black.
Fig. 4. Time evolution of the acceleration,
velocity and displacement. |
|
system A |
system B |
system C |
|
|
||
|
Event #1 (initial conditions)
|
||
|
|
|
|
|
|
|
|
|
Event #2
(final) |
||
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
EXERCISE
One person said that the cannon ball went straight up into the air
while another person said that the cannon ball followed a parabolic path. Surely,
both people cannot be correct !!! What is you view on the motion of the cannon ball? Think about the physical situation carefully and visualize the motion
of the ball. Setup a model so that you can make predictions about the balls
motion. Make a list of the physical quantities of interest that you can
calculate. Remember there are two observers Pat and Chris. Make a list of the approximations and simplifications necessary to
make your numerical predictions. Calculate the numerical values of the quantities in your list. Show a set of graphs illustrating the motion of the ball. Approximation and Simplifications Assume that the velocity of the truck is constant and travels on a
level road. We are concerned only with the flight of the cannon ball and
ignore the firing or landing of the cannon ball. Assume that the ball only
travels in a vertical plane and ignore any frictional effects. The
acceleration is assumed to be constant (does not change with time) such that The physical situation is complicated. We have two observers (Pat and
Chris) and two systems (truck and the cannon ball). Think about the situation by visualizing it. We can conclude that
from Pats point of view the truck remains stationary and the ball goes up
and down. Chris s point of view is that the truck
moves with a constant velocity and the ball also goes up then falls. To simplify the situation, we identity two systems and two frames of
reference.
Frame of reference
Event #1 ( Event #2 ( View
animation (figures 1 and 2) Pats frame of
reference: Initial values
Figure 5 shows the motion of the truck
and the cannon
ball from the frame of reference
of Pat. In
Pats frame of reference the truck does not move while the ball rises as it
slows down and stops at its maximum height and falls with increasing speed. Figure 6 show the variation in the components of the acceleration,
velocity and displacements as functions of time for the truck and cannon ball system in Pats frame of reference. The colour of
the line identifies the system (Truck: red and
Ball: blue). If two of the
results for the graph are the same, the colour is shown as black.
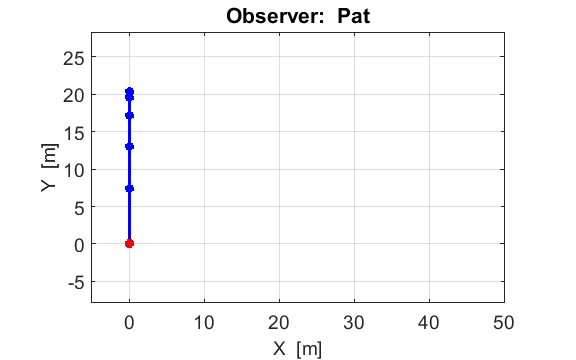
Fig. 5. The motion of the truck and cannon ball in Pats frame of
reference. The dots give the positions of the systems at 0.41 s time
intervals. From the spacing of the dots for the ball, we conclude that the ball
slows down going up and gets faster in falling.
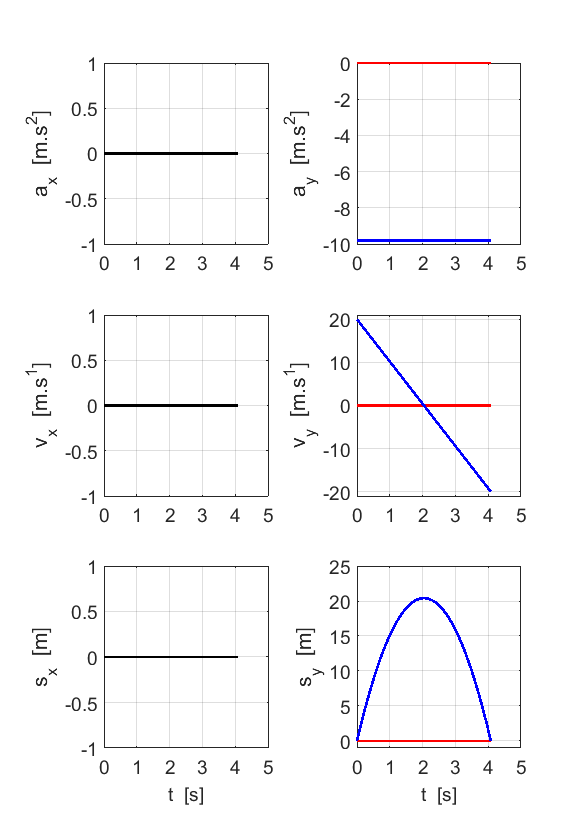
Fig. 6. Time evolution for
the motion of the truck and ball in the frame of reference of Pat. Red lines for truck. Blue
lines for ball. Black lines: tuck and ball have same values for the
motion. Calculations in Pats frame of reference Truck
The truck remains stationary
The truck does
not move, therefore, the above values for the truck do not change. Cannon Ball The ball only moves in a vertical direction along the Y
axis. Event # 1: (
Event #2 Ball reaches its
maximum height max
height time to reach maximum height maximum
height We know that
We know that
The ball reaches its maximum height of 20.4 m in
2.04 s. Event #3 Ball returns to
the cannon time to return to cannon velocity of
ball to return to cannon The motion is
symmetrical, the time it takes for the ball to fall back into the cannon is
twice the time it takes to teach its maximum height and the
velocity of the ball is We also can
calculate these quantities
The time of
flight of the cannon ball is 4.08 s and the velocity at the end of the flight
is 20 m.s-1 in a vertical downward direction. Chriss frame of reference: Initial values
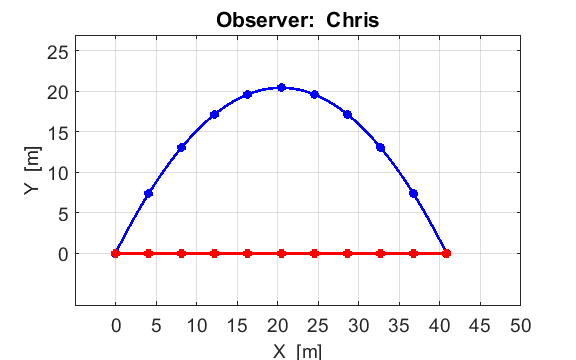
Figure 7 shows the motion of the truck
and the cannon
ball from the frame of reference
of Chris.
In Chriss frame of reference the truck moves at a constant velocity while
the ball rises as it slows down and stops at its maximum height and falls
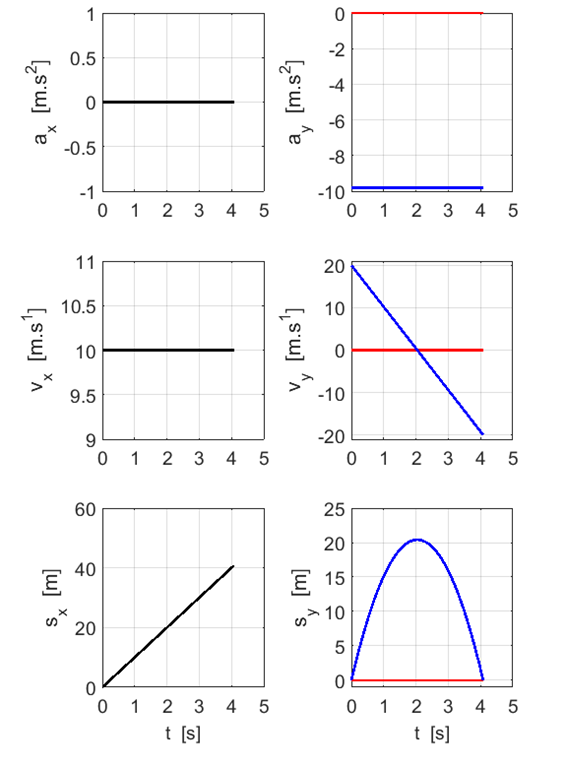
with increasing speed. Figure 8 show the variation in the components of the acceleration,
velocity and displacements as functions of time for the truck and cannon ball system in Chriss frame of reference. The colour
of the line identifies the system (Truck: red and
Ball: blue). If two of the
results for the graph are the same, the colour is shown as black.
Fig. 7. The motion of the truck and cannon ball in Chriss frame of
reference. The dots give the positions of the systems at 0.41 s time
intervals. From the spacing of the dots for the
ball,
we conclude that the ball slows down going up and gets faster in falling. The
trajectory of the ball is a parabola. The spacing of the red dots are uniform, therefore, the speed of the
truck is uniform (constant).
Fig. 8. Time evolution for
the motion of the truck and ball in the frame of reference of Chris. Red lines for truck. Blue
lines for ball. Black lines: tuck and ball have same values for the
motion. For the ball, the Calculations in Chriss frame of reference Cannon Ball Event # 1: (
Event #2 Ball reaches its
maximum height max
height time to reach maximum height maximum
height
We know
that
We know
that
The ball reaches its maximum height of 20.4 m in
2.04 s. Event #3 Ball returns to
the cannon time to return to cannon velocity of
ball to return to cannon The motion is
symmetrical, the time it takes for the ball to fall back into the cannon is twice
the time it takes to teach its maximum height and the
velocity of the ball is We also can
calculate these quantities
The final
velocity of the ball is
In the +X
direction the ball
moves with a constant velocity of 10 m.s-1. The X
displacement of the ball during the flight is Truck
The truck
moves with a constant velocity
which is the same as the ball. Therefore, the ball is always vertically above
the truck. At the end of the flight of the ball will land back into the mouth
of the cannon. Figure 9 and figure 10 shows the paths of
the cannon ball relative to Pat
and Chris as observers. Both agree
the ball goes up and back down again.
Fig. 9. The trajectory of the cannon ball and truck from Pats frame of reference.
Fig. 10. The trajectory of the cannon ball and truck from Chriss frame of reference We can see from figure 7 and figure 10 that both Pat and Chris are
correct in describing the trajectory of the ball. Pat see the ball rise and fall only in a
vertical direction, however, Chris see a parabolic trajectory for the ball. Motion is a relative concept and depends upon the motion of an
observer |
|
Ian Cooper School of Physics University of Sydney If you have any feedback, comments,
suggestions or corrections please email Ian Cooper ian.cooper@sydney.edu.au |