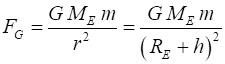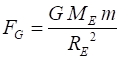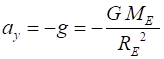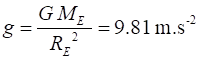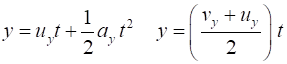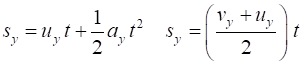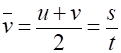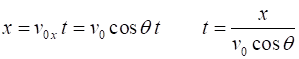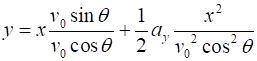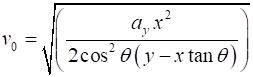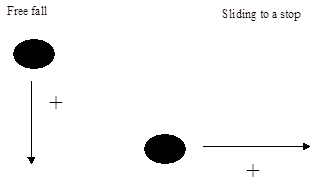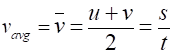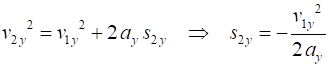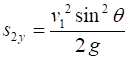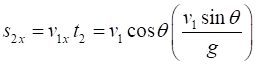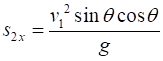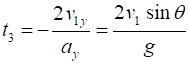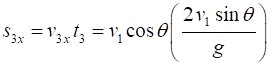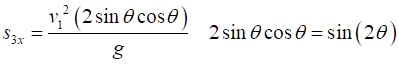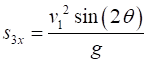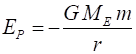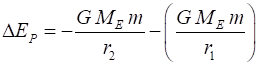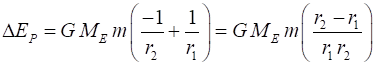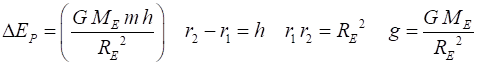MODULE 5
ADVANCED MECHANICS
PROJECTILE MOTION
|
The magnitude of the gravitational
force FG on
an object of mass m in the Earths gravitational field
is (1) where G is the Universal Gravitational
Constant, ME is the mass of the Earth, RE is the radius of the Earth, r is the distance from the Earths centre
to the object and h is the distance of the object above
the Earths surface. Just above the Earths surface h << RE,
so, (RE + h) RE. Therefore, we can assume the
gravitational force FG near the surface of the Earth is constant
and acts in direction vertically towards the surface (2) The simplest type of motion in a gravitational field near the surface of the Earth is called projectile motion.
As an object of mass m moves near the surface of the
Earth, the net force acting on the object is the gravitational force FG given by equation (2). In projectile motion problems, the first step is to define your
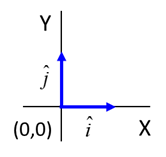
[2D] frame of reference (Origin O(0,0); + X and + Y
axes).
[2D] frame of reference We can apply Newtons Second Law to
the object near the Earths surface Hence, we can conclude that near the
Earths surface, the acceleration due to gravity g is constant (3) where g is taken as a positive constant and
its value is For projectile motion, you always considered the motion of an
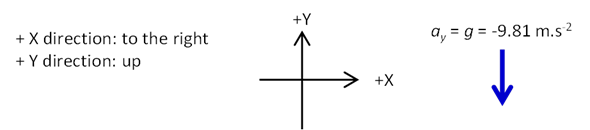
object along the X axis and the along the Y axis as two independent
components: X axis (horizontal motion) ax = 0, vx = constant Y axis (vertical motion) ay = -g = - 9.81 m.s-2 where vertically up is taken as the +Y
direction and horizontally to the right as the +X direction. The acceleration |
|
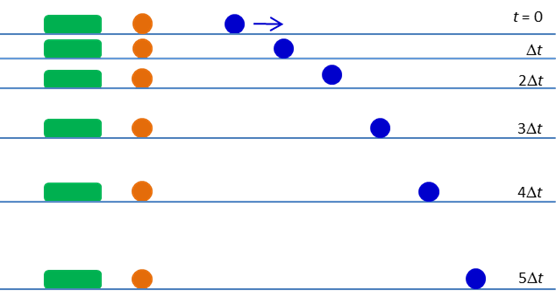
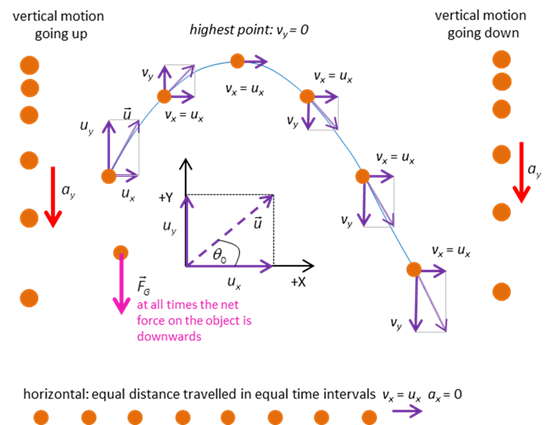
Figure 1 shows the positions three
objects dropped from rest at equal time intervals. The objects have different
shapes and masses while the third object is initially projected horizontally.
All three objects fall at the same rate such that the horizontal acceleration
is zero, ax = 0 and the vertical acceleration
is constant, ay = -g. The
horizontal velocity vx is constant while the magnitude of
the vertical velocity vy continually increases as it falls.
Fig.
1. Three different objects fall at
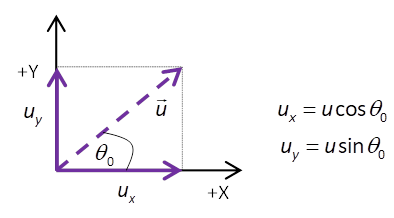
the same rate. Consider an object projected with an
initial velocity
Given the initial conditions
(displacement and velocity at time t = 0), the equation for uniform
acceleration can be used to calculation the objects displacement (x or sx, y or sy) and velocity (vx, vy) at any time t.
Note:
Straight line graph ( v vs t ) Parabolic graph ( s vs t ) Beware: there is no unique set of symbols for
displacement, velocity or acceleration.
The most common symbols for initial velocity are Figure 2 shows the parabolic trajectory travelled
by an object that was launch with an initial velocity
Fig. 2. The parabolic trajectory of an object when the net force acting on it is the gravitational force. |
|
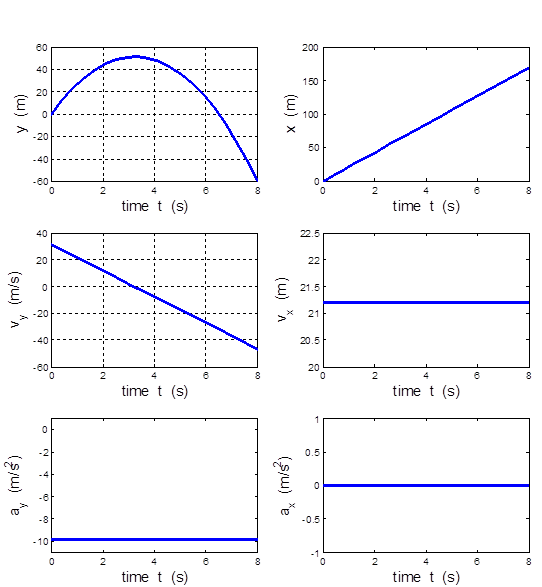
Exercise 1 From the graphs estimate the initial
launch velocity
|
|
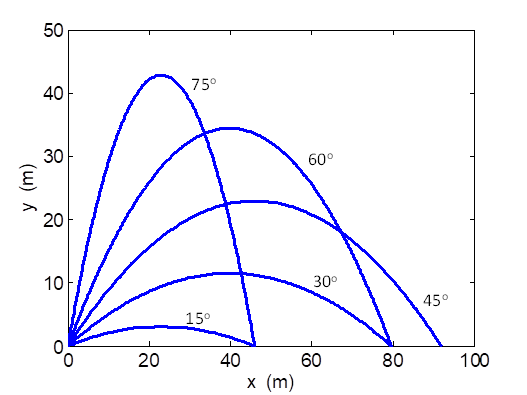
Exercise 2 Figure 3 shows the trajectory of a projectile fired with a
constant magnitude for its initial velocity but at different angles. Note:
from figure 3 that the maximum range of
a projectile occurs when the launch angle is 45o. For angles lower or greater than 45o
the range is less. This implies that two launch angles will give the same
range.
Fig. 3. Trajectories of
a projectile launched at different angles, but with the same magnitude for
the initial velocity. |
|
|
From the information provided in figure 3 estimate the magnitude of the initial velocity. Check your answer by doing further calculations to confirm your answers from the graph. |
|
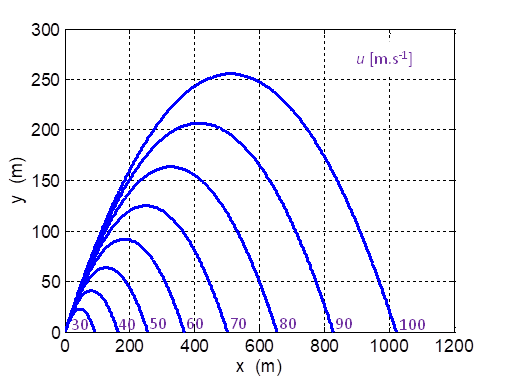
Exercise 3 Figure 4 shows the trajectory of a projectile launched at 45o
w.r.t. the horizontal for a range of initial velocities.
Fig.
4. Trajectories of a projectile
launched at 45o w.r.t the horizontal, but with different launch
speeds. What would be the result of increasing and increasing the launch speed? As the launch speed gets bigger and bigger, can we still take g as a constant? Explain. |
|
Exercise 4 A
volcano that is 3300 m above sea level erupts and sends rock fragments
hurting into the sea 9.4 km away. If the fragments were ejected at an angle
of 35o, what was their initial speed? Solution
Identify / setup v0 = ? m.s-1 q = 35o
x0 = 0 y0
= 0
x = 9400 m y
= -3300 m
ax = 0 ay
= -9.8 m.s-2 v0x = v0cosq v0y = v0sinq Equation for uniformly accelerated motion
Execute X motion Y Motion Eliminate t to find
equation for v0
Evaluate The rocks in a volcanic explosion
can be thrown out at enormous speeds. |
|
Exercise 5 In the
Blackhawk landslide in California, a mass of rock and mud fell 460 m down a
mountain and then travelled 8 km across a level plain on a cushion of
compressed air. Assume that the mud dropped with the free-fall acceleration
due to gravity and then slide horizontally with constant deceleration. (a)
How long did it take the mud to drop 460 m? (b) How fast was it travelling
when it reached the bottom? (c) How long did the mud take to slide the 8 km
horizontally? Solution
a = g = 9.8 m.s-2 vo = 0
s = 460 m time to fall
vertically, t = ? s velocity at
bottom of mountain, v = ? m.s-1 Since a = constant (a) s
= vo
t+ a t2 t = (2s / a) = {(2)(460)/9.8}
s = 9.7 s (b) v
= vo
+ a t v
= 0 + (9.8)(9.7) m.s-1 = 95
m.s-1 (c) Sliding to a stop vo
= 95 m.s-1 s = 8x103 m v
= 0 a = ? m.s-2 time to slide to
a stop, t = ? s Since a = constant v2 = vo2
+ 2 a s
0 a
= (v2 vo2)/(2s)
a
= (- 952 / 16103) m.s-2 = - 0.56 m.s-2 v = vo +
a t t = - vo / a = - 95 / (-0.56) s = 170 s |
|
Galileos Analysis of Projectile Motion Our
understanding of projectile motion owes a great debt to Galileo, who in his work
entitled Dialogues Concerning Two New Sciences,
presented his classic analysis of such motion. Galileo argued that projectile motion was a
compound motion made up of a horizontal and a vertical motion. The horizontal motion had a steady speed in
a fixed direction, while the vertical motion was one of downwards
acceleration. Using a geometric
argument, Galileo went on to show that the path of a particle undergoing such
motion was a parabola. In his work, Galileo admits that his assumptions and
results are only approximations to the real world. He admits that due to resistance of the
medium, for instance, a projectiles horizontal motion cannot be truly
constant in speed. He states quite
clearly that the path of the projectile will not be exactly parabolic. He argues, however, that his approximations
can be shown by experiment to be close enough to the real world to be of very
real use in the analysis of such motion.
In doing this, he became perhaps the first scientist to demonstrate
this modern scientific attitude. His
approach was certainly very different from that of the ancient Greek
geometers, who were only interested in exact results. |
|
|
|
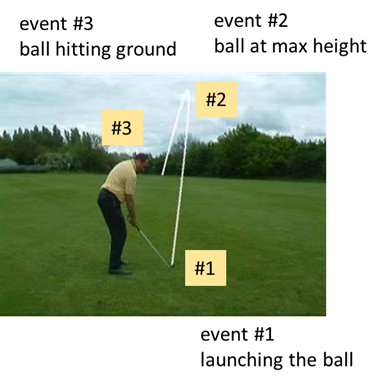
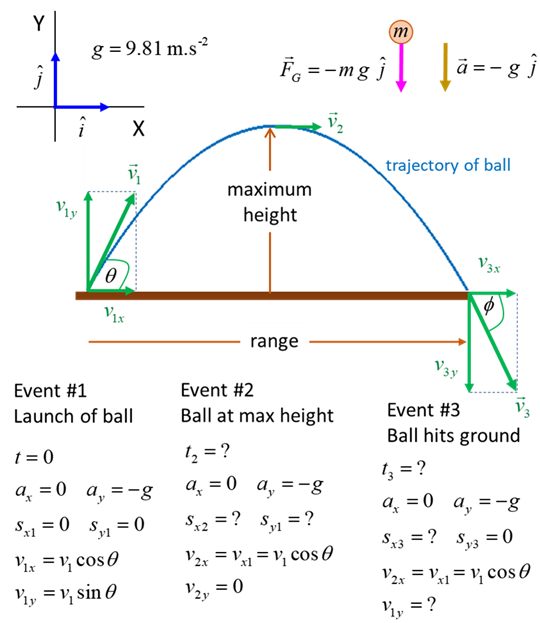
Exercise 6 Studying
Projectile Motion Consider
a ball projected from ground level with an initial velocity
What calculations are necessary for our predictions? What would a physicist do? The
first step is always to visualize the physics situation and think about how
you might solve the problem. For example, image you are looking at the flight
of a golf ball and know that the motion is described
by the equations of uniform motion.
Draw
an animated scientific diagram of the physical situation. The diagram should
include known and unknown physical quantities. In this example, we can
identify three separate events: #1 launching the ball; #2 ball reaches its
maximum height and #3 the instant before the ball hits the ground. Using
subscripts in an easy way to keep track of the parameters. If you want to
improve your physics, you need to good at using appropriate symbols and
subscripts.
The equations for uniform
accelerated motion are
These equations need to be applied to the X motion and Y motion
separately and by using subscript we can identify the times for our three
events. Event #1 launching the ball
Note: The horizontal acceleration is zero Event #2 ball reaches its maximum height (vertical
velocity of ball is zero)
Time to reach maximum height
Maximum height
Horizontal displacement at maximum height
Event #3 instant before ball hits ground (vertical
displacement of ball is zero)
Time just before impact with ground
Note: It takes twice the time to hit the ground as it takes for
the ball to reach its maximum height Range of ball just before it hits the ground
Note: The range is twice
the distance from the launch position to the horizontal position of the
maximum height The maximum range occurs when the launch angle is 45o Velocity of the ball just before impact
Note: the magnitudes of the initial velocity at launch and the velocity
at impact with the ground are equal. The horizontal components are equal and
the vertical components have equal magnitudes are in opposite directions. |
|
|
Exercise 7 A ball was launched from ground level with a speed of 3.24 m.s-1 at an angle of 60o w.r.t
to the horizontal. Calculate:
Maximum
height the reached by the ball.
Time
for the ball to reach its maximum height.
Horizontal
displacement of the ball at its maximum height position.
The
acceleration of the ball (vector) at its maximum height.
The
time of flight.
The
horizontal range of the ball.
The
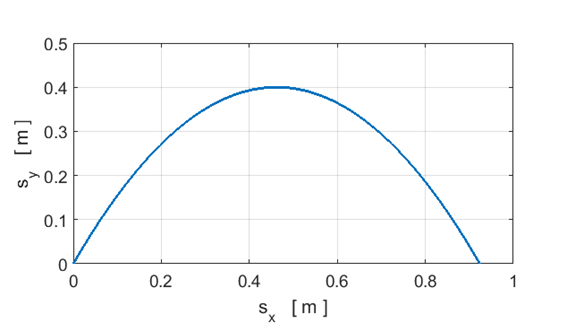
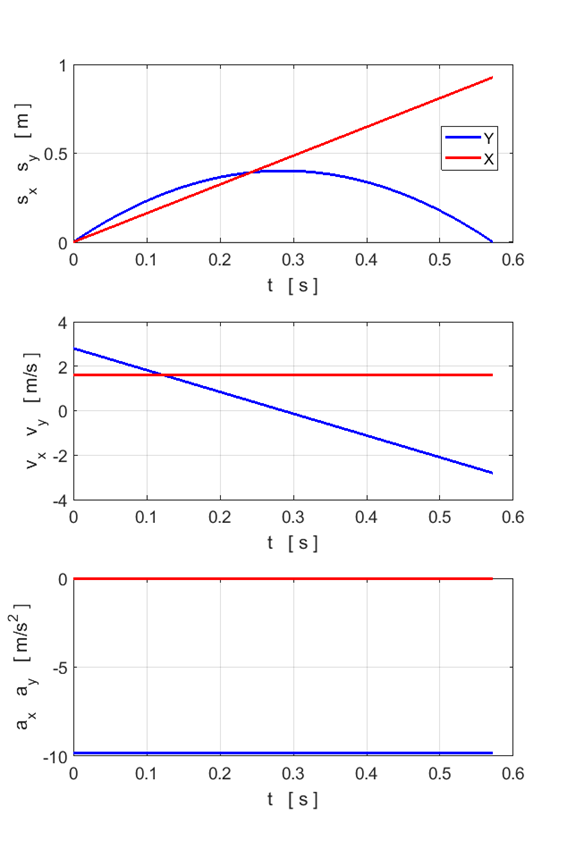
impact velocity of the ball with the ground. Check your answers by studying the graphs below.
Trajectory of the
Ball.
Graphical
representation of the ball in flight. You must do the experiment on the Video Analysis of the Flight of
a golf Ball. The experiment is best done in class at your school in a group
of three. However, the experiment can also be done individually as no
equipment is necessary other than pen, paper, graph paper, ruler and
calculator. The measurements are best recorded
in a spreadsheet to save time and effort. |
|
Maths Extra The gravitational potential energy
is given by Consider raising an object of mass m
near the surface without increasing its kinetic energy. As a consequence,
work must be done on the object to increase the potential energy of the
object / Earth system.
Initial position Final
position
Work done = Increase in Gravitational Potential Energy
|
|
Ian Cooper School of Physics University of Sydney If you have any feedback, comments,
suggestions or corrections please email Ian Cooper ian.cooper@sydney.edu.au |