VISUAL PHYSICS ONLINE

MODULE 5

ADVANCED MECHANICS

TORQUE AND ROTATIONAL MOTION

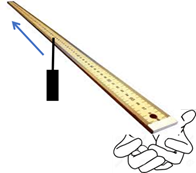
TORQUE AND THE VECTOR (CROSS) PRODUCT

Hold on to the end of a metre rule with an object dangling from it. Slide the object from near your hand to the other end of the meter rule and feel the ruler twist. The weight of the object is the same and so the force acting on your hand is the same. What is different is the torque that you experience.

Torque is the rotational counterpart of force. Forces tend to change the motion of things. Torques tend to twist or change the state of rotation of things.

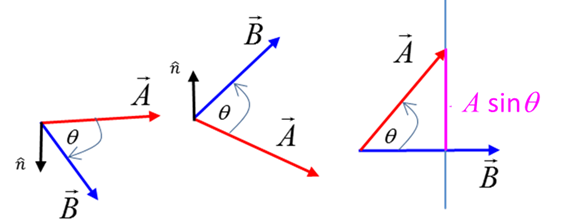
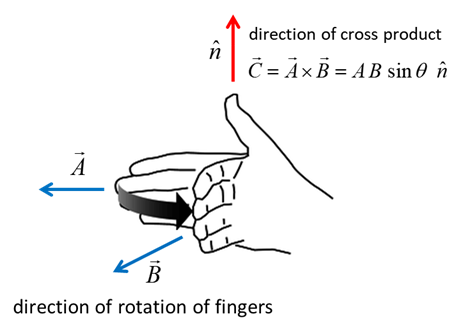
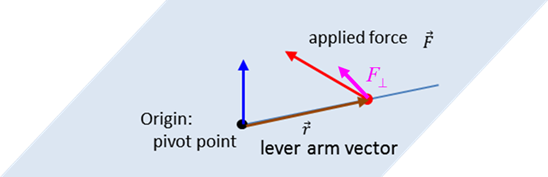
To better understand the concept of torque, we will consider the vector product of two vectors. This treatment is not normally done at a school level. However, the more mathematical treatment makes it easier to appreciate and correctly apply the concept of torque.

The vector product or cross product of two vectors and is defined as

The magnitude of the vector is .

The vector is a unit vector which is perpendicular to both the vectors and .

The angle between the two vectors is always less than or equal to 180^o. The sine function over this range of angles is never negative, hence the magnitude of the vector product is always positive or zero .

The direction of the vector product is perpendicular to both the vectors and . The direction is given by the right-hand screw rule. The thumb of the right hand gives the direction of the vector product as the fingers of the right hand rotate from along the direction of the vector towards the direction of the vector.

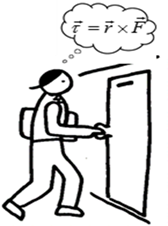
What is the physics of opening a door?

It is the torque applied to the door that is important and not the force.

Torque (tau) S.I. unit N.m

A force can cause an object to move and a torque can cause an object to rotate. A torque is often thought of as a force multiplied by a distance. However, using the idea of the vector (cross) product we can precisely define what we mean by the concept of torque.

The vector is the torque applied, the vector is the lever arm distance from the pivot point to the point of application of the force . The angle is the angle between the vectors and . The direction of the torque is found by applying the right-hand screw rule: the thumb points in the direction of the torque as you rotate the fingers of the right hand from along the line of the vector to the vector . The torque is perpendicular to both the position vector and the force .

The magnitude of the torque can be expressed as

where is the component of the applied force which acts at right angles to the radius vector .

The equation for the torque can also be expressed as

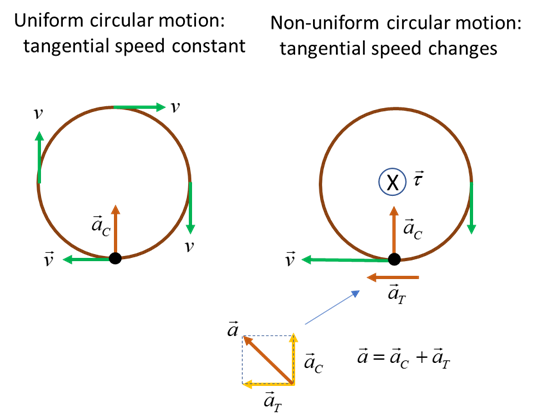
A non-zero net force acting on an object causes it to accelerate in the direction of the force (Newton’s 2^nd Law of motion). However, a net toque acting on an object is necessary to cause an angular acceleration of an object.

In uniform circular motion, the tangential speed of the object is constant. To change the tangential speed, a non-zero torque must act on it, producing a tangential component of the acceleration. The acceleration of the object has two components – the centripetal acceleration (directed towards the centre) and a tangential component (directed along the tangent to the circle).

Example

A helmsmen exerts the forces on a wheel of a yacht as shown in the diagram. The radius of the wheel is 0.74 m. In each case, calculate the applied torque and state the direction of the torque and the direction in which the wheel will rotate.

Solution

The applied torque is given by

Radius of wheel

Applied forces

The torque is directed into the page (right-hand screw rule) and the wheel will turn in a clockwise sense.

The torque is directed out of the page (right-hand screw rule) and the wheel will turn in an anticlockwise sense.

The torque is directed out of the page (right-hand screw rule) and the wheel will turn in an anticlockwise sense.

The repeated calculations can be done using EXCEL or MATLAB. Work through the Matlab script to gain a better understanding of how to do the calculations.

% radius

r = 0.74;

% Force magnitudes

F = [45 54 75];

% Angles

theta = [90 50 75];

% Torques

tau = r .* F .* sind(theta)

RECAP

To loosen a tight nut with a spanner as shown in the figure, you need to apply a torque that gives an anticlockwise rotation. From experience you know that if you apply a force as far as possible from the nut, it is more likely that the nut will turn. If you apply a force to the spanner near the nut it might turn but it would require a larger effort than applying the force at the far end of the spanner. Notice that the force 1 and 2 would loosen the nut as the applied torques produce anticlockwise rotations, but force 3 would tighten the nut further because it produces a clockwise torque.

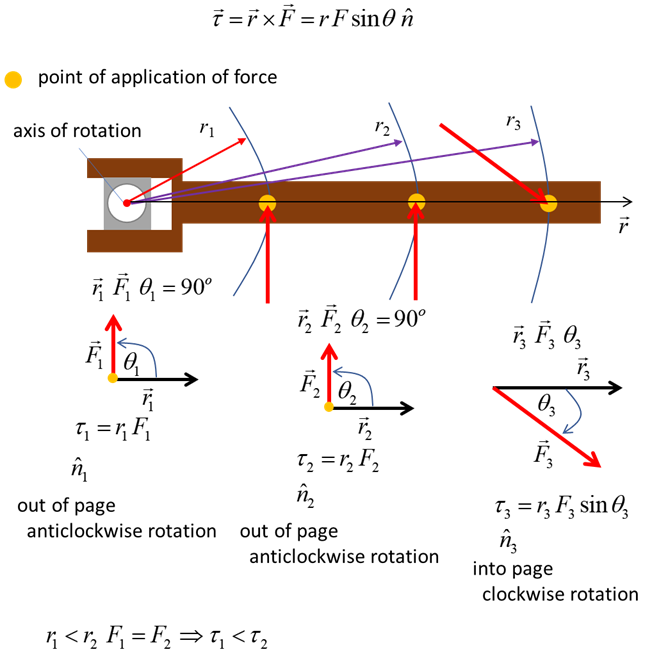
In answering questions on torque you need to identify the axis of rotation and the pivot point, the point of application of the force, the vector which corresponds to the displacement vector pointing from the pivot point to the point of application of the force (lever arm vector), the force acting at the point of application and the angle between the vectors and . Then apply the equation for the torque . The right-hand screw rule is then used to determine the direction of the torque.

Note: The equation given in the Physics Stage 6 Syllabus for the torque is incorrect

you simply cannot multiple two vectors together

Ian Cooper

If you have any feedback, comments, suggestions or corrections please email

matlabvisualphysics@gmail.com