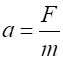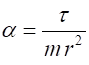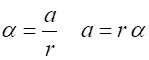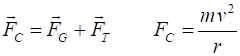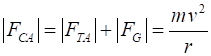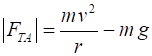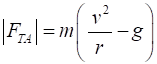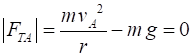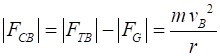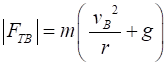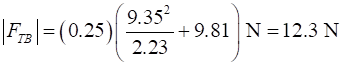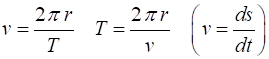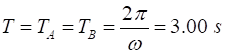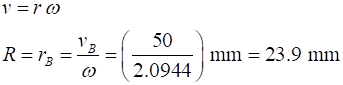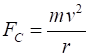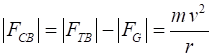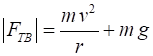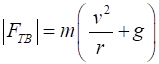MODULE 5
ADVANCED MECHANICS
CIRCULAR MOTION
|
A non-zero net force acting on an
object causes it to accelerate in the direction of the force (Newtons 2nd
Law of motion). However, a net toque acting on an object is necessary to
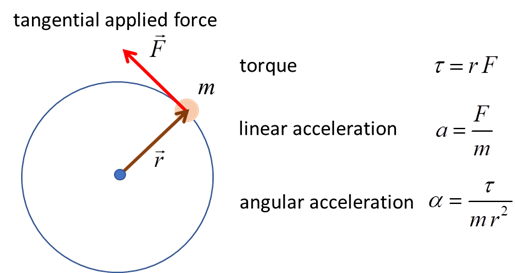
cause an angular acceleration of an object. Consider a small object of mass m
connected to an
axis of rotation by a light rod of length r. If a tangential force of magnitude F
is applied to
the object, it will move with an acceleration a given by Newtons Second Law and the
torque Hence,
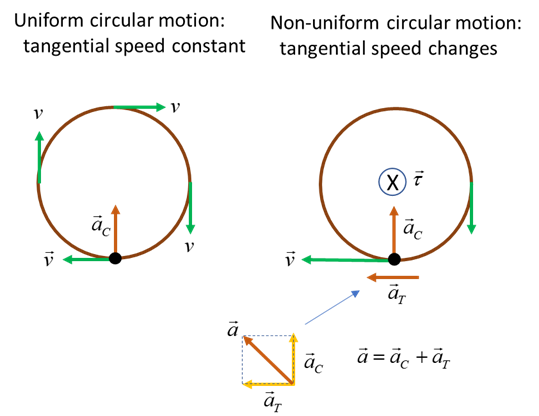
In uniform circular motion, the
tangential speed of the object is constant. To change the tangential speed, a
non-zero torque
When an object moves in a circle of radius R with constant speed v, the acceleration ac is always directed towards the centre of the circle and is called the centripetal acceleration. The force FC that produces the centripetal acceleration must also be directed towards the centre of the circle and is called the centripetal force.
|
|
View the animations of an object executing motion in a circle.
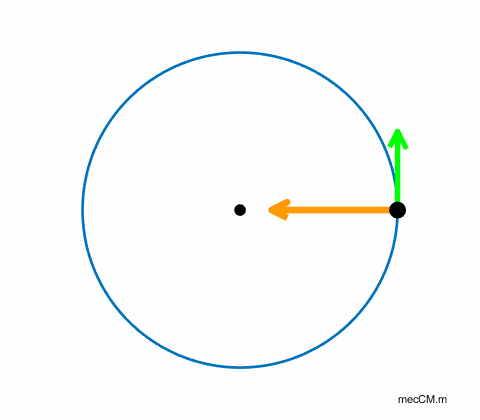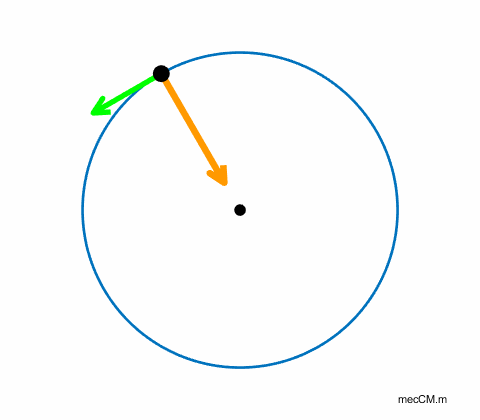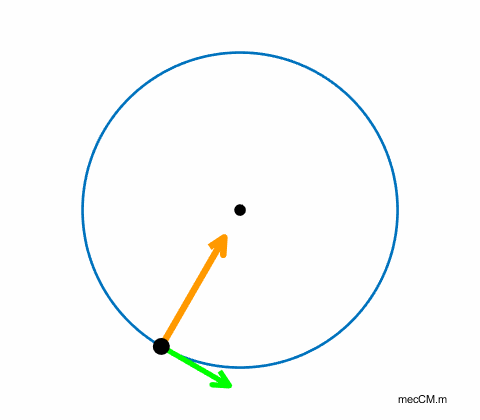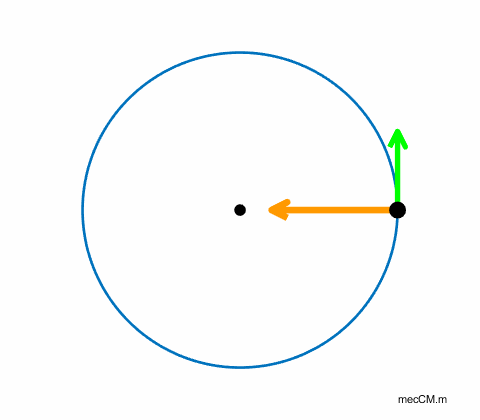
Uniform circular motion: The green arrow represents the tangential velocity. The magnitude of the tangential velocity is constant. However, the direction of the object is always changing. Therefore, the object is accelerating. The orange arrow represents the centripetal acceleration which is always directed towards the centre of the circle.
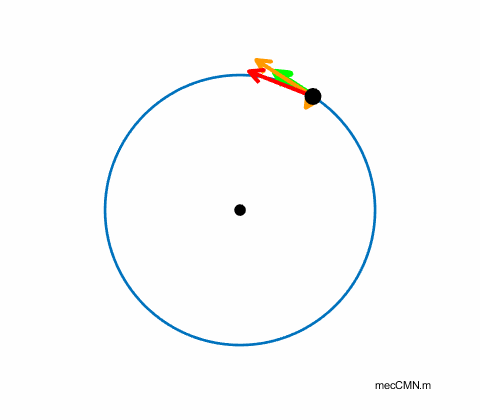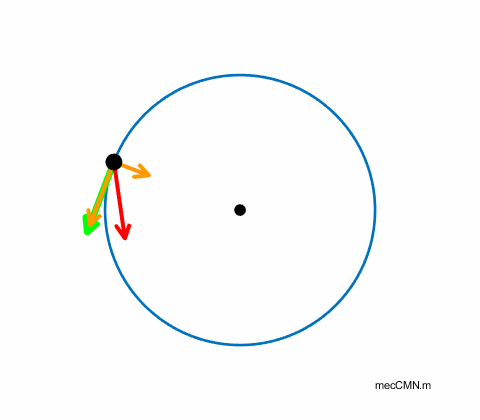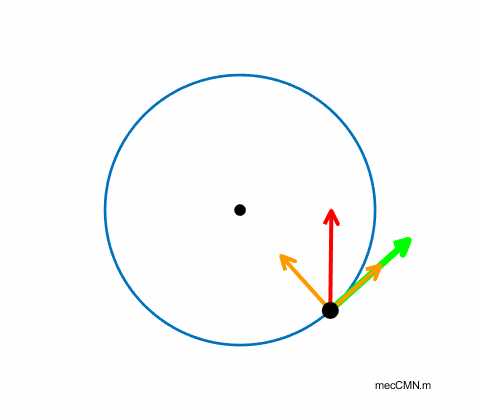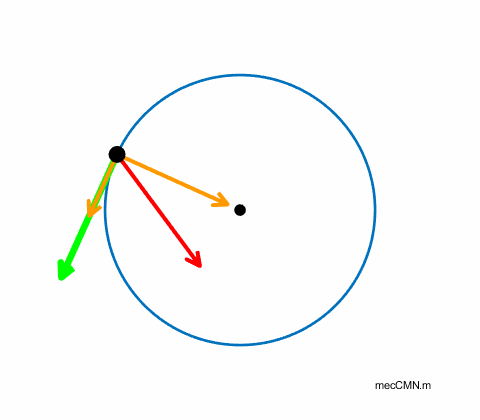
Non-uniform circular motion: The object experiences a constant torque exerted by a tangential force applied to the object. Therefore, the object moves with a constant angular acceleration and so produces a tangential acceleration which results in a continual increase in the tangential speed of the object. The objects direction is always changing as it moves along its circular path. So, there must be a component of acceleration directed towards the centre of the circle which we call the centripetal acceleration. The linear acceleration of the object is the vector sum of the tangential and centripetal accelerations As the tangential speed of the object increases, it continuously changes direction more rapidly. Hence, the centripetal acceleration must also continually increase. The relationship between the centripetal acceleration aC and tangential speed v for an object moving in a circle of radius R is |
|
Note: in this example the speed of the ball changes, however, it
is still true that a force equal to the centripetal force is needed to hold
the ball in its circular orbit. When the ball is at point A, the centripetal force is the sum of
the string tension and the gravitational force (weight of ball).
|
|
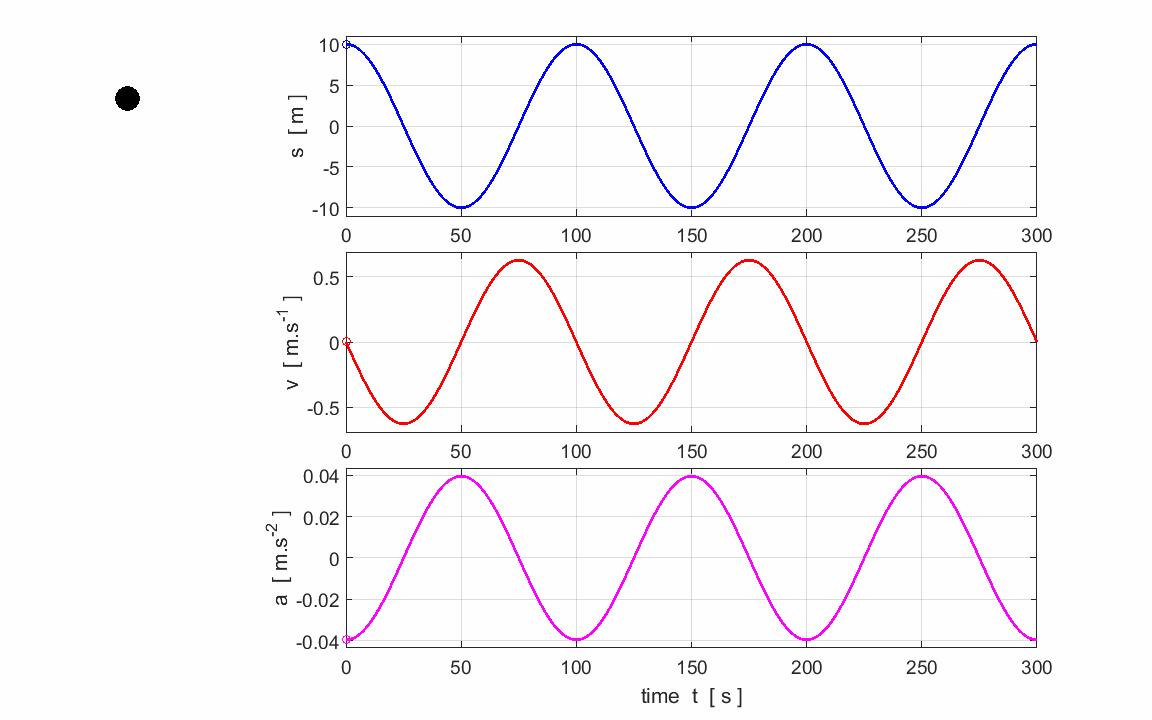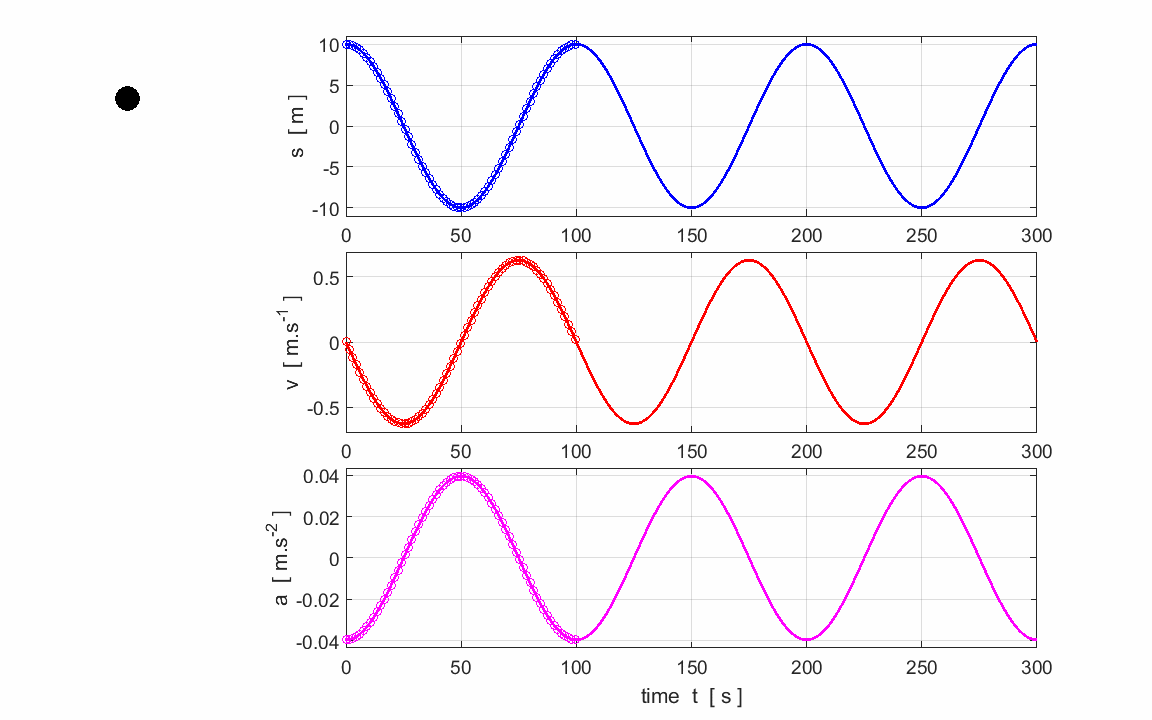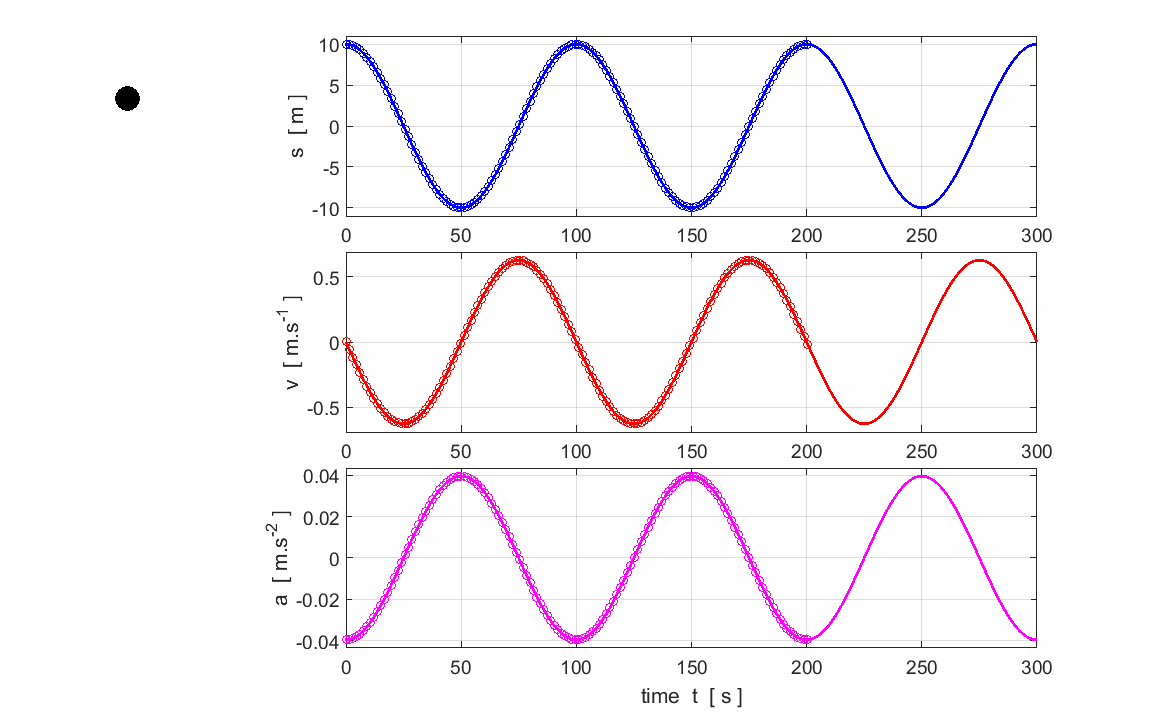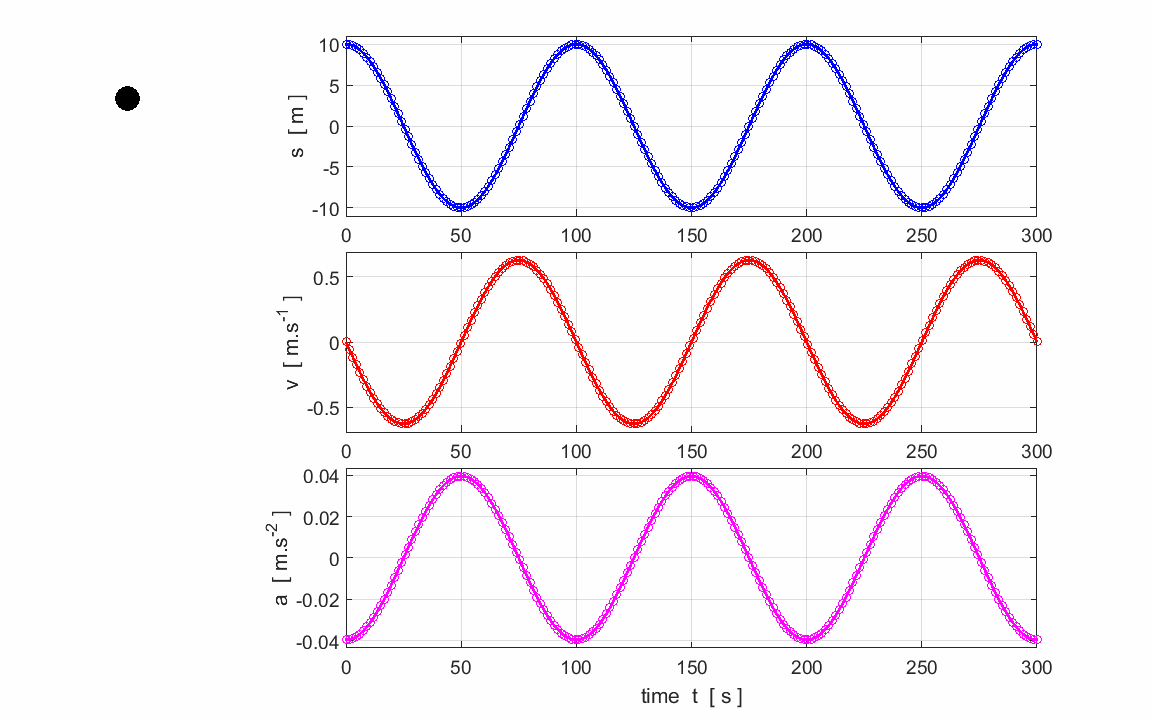
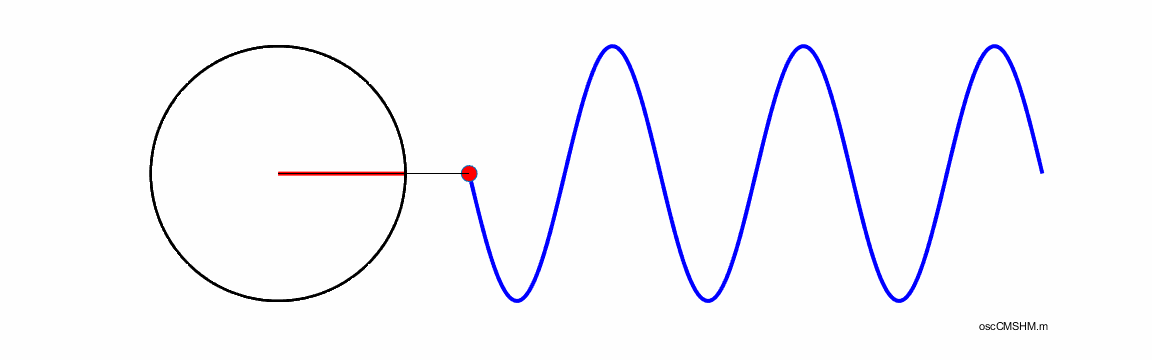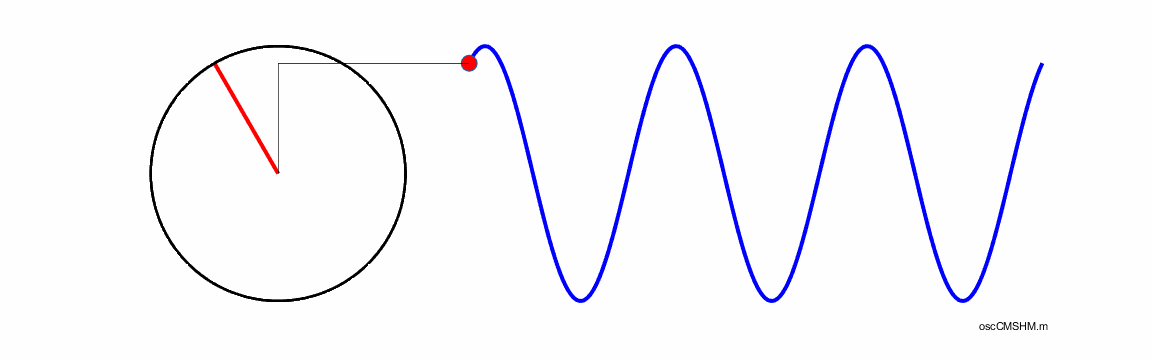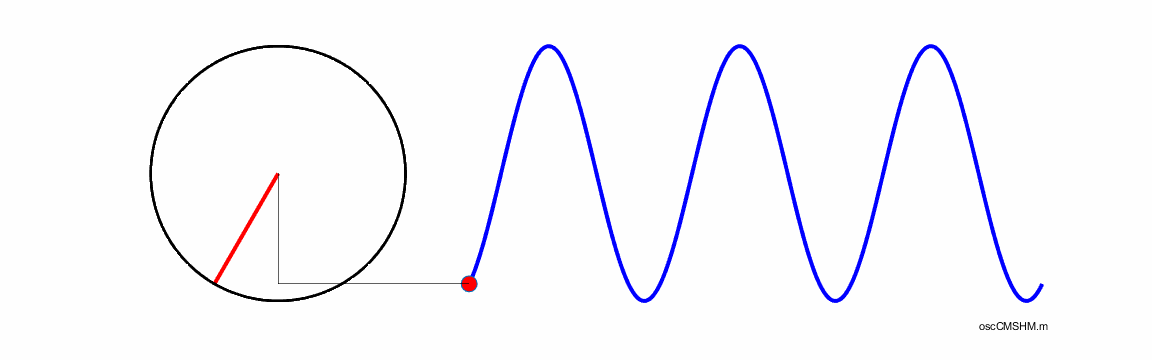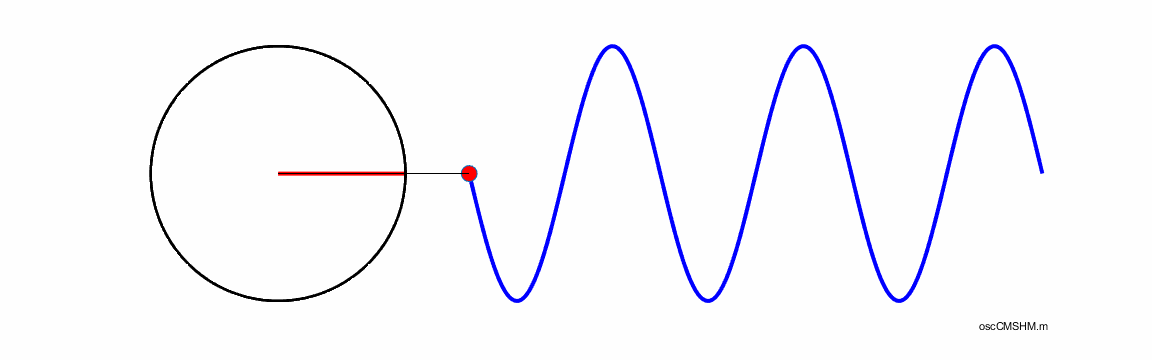
What is the connection between uniform circular motion and simple
harmonic motion? The
displacement s
for an object attached to a vertical spring that is
oscillating up and down about the equilibrium is given by the equation where
R is the amplitude of the motion
and t is
the time. But where does the angle
Uniform
circular motion describes the movement of an object traveling a circular path
with constant tangential speed v.
The one-dimensional projection of this motion can be described as simple
harmonic motion. In uniform circular motion, the velocity vector If
an object moves with angular velocity
For
the circular motion, the radius vector sweeps out one complete revolution in
a time T which
is known as the period. Hence the frequency f of the circular motion is f = 1/T and the rate at which the radius vector
rotates at is given by the angular speed (angular frequency)
But, this time T is corresponds precisely to the time it takes for the object to oscillate up and down through one cycle of the simple harmonic motion. Thus, the projection on the Y-axis of an object rotating in a circle has the same motion as the object undergoing simple harmonic motion. Indeed, we can say that the projection of circular motion onto a straight line is simple harmonic motion. Consider an
object executing uniform circular motion with a radius r
and speed v .
The time for one complete revolution is known as the period T. The distance travelled by the
object in one period is simply the circumference of the circle
|
|
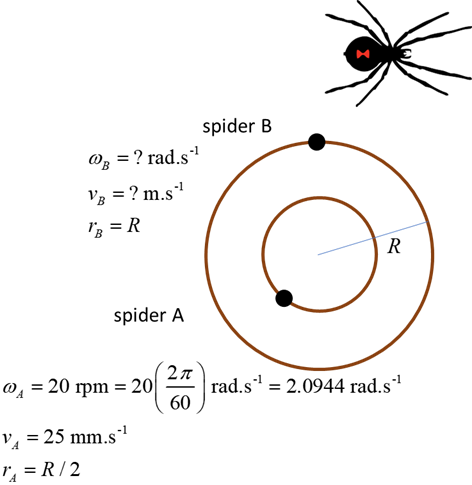
Example Image a spider sitting halfway between the rotational axis and
the outer edge of a turntable. When the turntable has a rotational speed of
20 rpm, the spider has a speed of
25 mm.s-1. What will be the rotational speed and tangential speeds of
another spider sitting on the outer edge? What are the periods for the two spiders? What is the radius of the turntable? Solution Visualize
the problem / how to approach the problem? / annotated scientific diagram
All parts of the turntable have the same rotational speed
(angular speed or angular velocity) and hence the same period. Alternatively, for the period: 20 rpm = 20
revolutions in 60 seconds 1 revolution in 3
seconds T = 3.00 s Tangential speed Radius of turntable R |
|
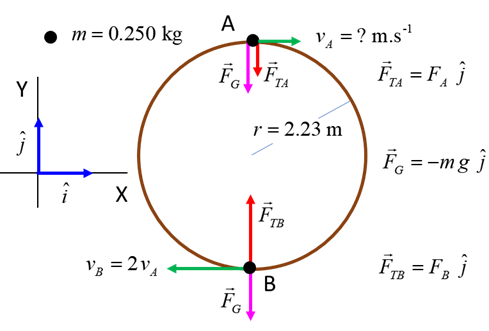
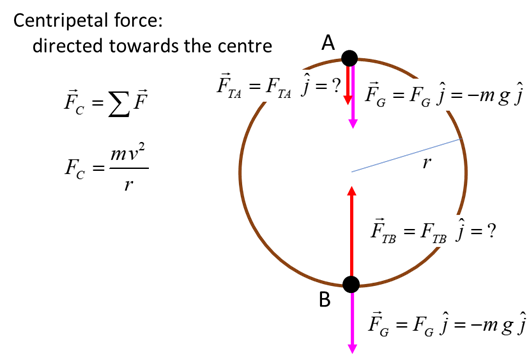
Example A ball of mass m is rotated at a constant speed v
in a vertical
circle of radius r. Find the tension in the string at
positions A and B. Solution
We know that a force equal to the centripetal force is needed to
hold the ball in its circular orbit. When the ball is at point A, the centripetal force is the sum of
the string tension and the gravitational force (weight of ball).
Note: The tension in the string becomes zero when
When the ball is at point B, the centripetal force on the ball
still must be and the must be equal to the net force acting on the ball at
this point
Note: The centripetal force at point B is larger than at point A
since it must support the weight of the ball and act so that the ball moves
in its circular path. |
|
Ian Cooper School of Physics University of Sydney If you have any feedback, comments,
suggestions or corrections please email Ian Cooper ian.cooper@sydney.edu.au |