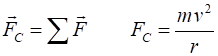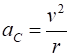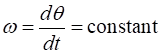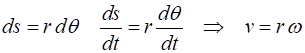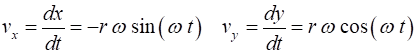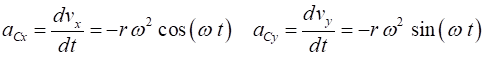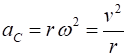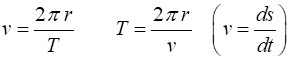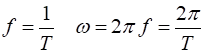VISUAL PHYSICS ONLINE

MODULE 5

ADVANCED MECHANICS

UNIFORM CIRCULAR MOTION

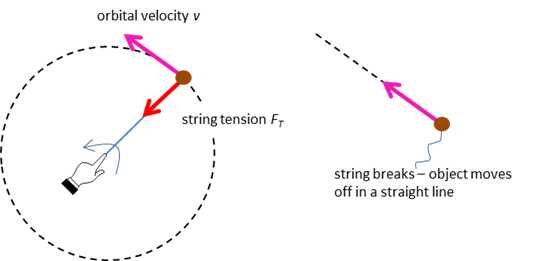
Uniform circular motion is circular motion with a uniform tangential (orbital) speed. As an example of circular motion, imagine you have a rock tied to a string and are whirling it around your head in a horizontal plane. Because the path of the rock is in a horizontal plane, as shown in the diagram, gravity plays no part in its motion. The Greek, Aristotle, considered that circular motion was a perfect and natural motion, but it is far from it. If you were to let go of the string, the rock would fly off at a tangent to the circle - a demonstration of Newton's First Law of Motion (an object continues in uniform motion in a straight line unless acted upon by a force). In the case of our rock, the force keeping it within a circular path is the tension in the string, and it is always directed back towards the hand at the centre of the circle. 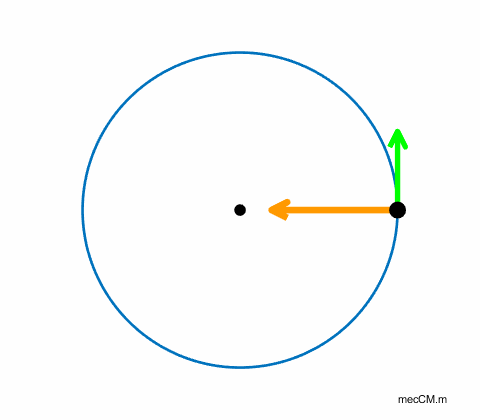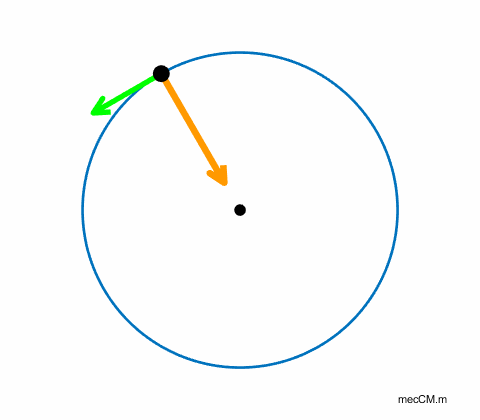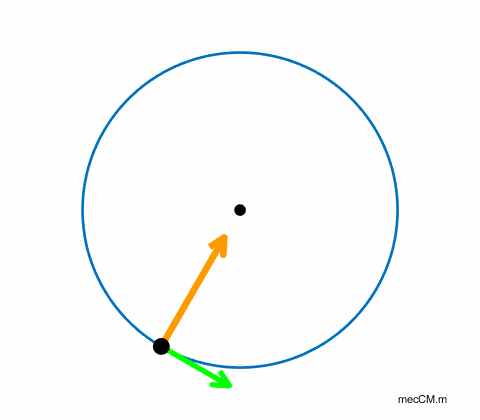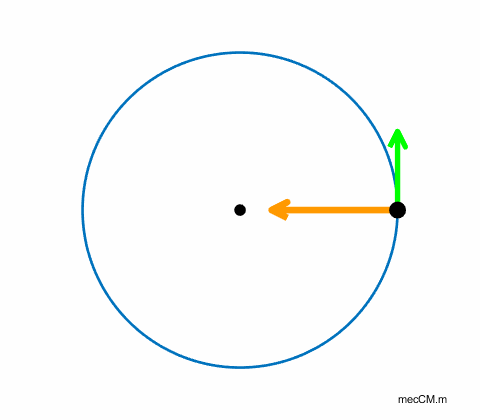Without that force the rock will travel in a straight line (figure 1).

Fig. 1. A force acting towards the centre of a circle is necessary for an object to rotate in a circular path.

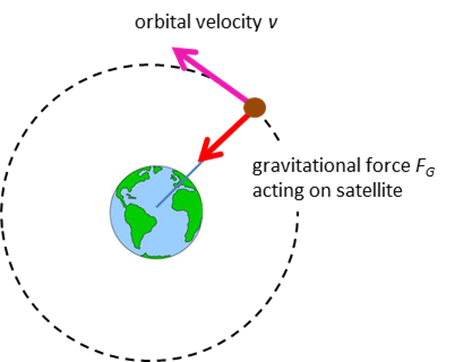
If the magnitude of the velocity is constant but its direction is changing, then the velocity must be changing, so, the rock is accelerating. A force is required to accelerate the rock and as stated above, this force is the tension in the string. This centre seeking force is called the centripetal force . The term centripetal force is only a label attached to real physical forces such as tension, gravitation or friction. On force diagrams, you should show the real physical forces acting and not the label centripetal force.

The same is true of a spacecraft in orbit around the Earth, or any object in circular motion - some force is needed to keep it moving in a circle or accelerate it and that force is directed towards the centre of the circle. In the case of the spacecraft, it is the gravitational attraction between the Earth and the spacecraft that acts to maintain the circular motion and keep it in orbit. The Moon obits around the Earth and the Earth around the Sun because of the gravitational force like the satellite shown in figure 2.

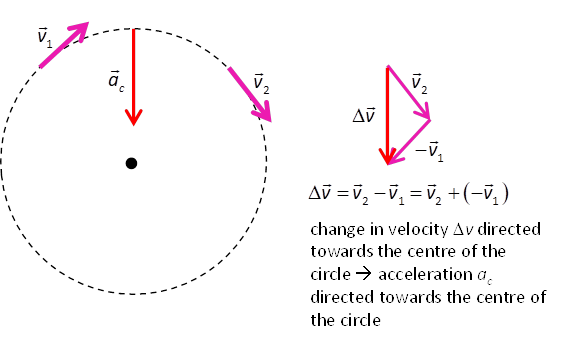
Fig.2. A satellite is acted upon by the gravitation force between the Earth and the satellite. The centripetal force is the gravitational force.

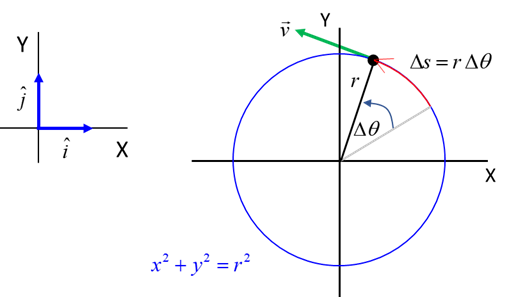
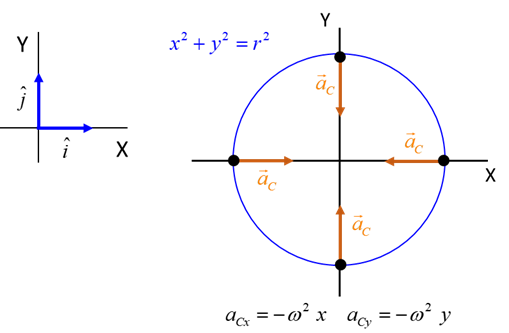
An object is shown moving between two points (1) and (2) on a horizontal circle in figure 3. Its velocity has changed from to . The magnitude of the velocity is always the same, but the direction has changed. Since velocities are vector quantities, we need to use vector mathematics to work out the average change in velocity . In this example, the direction of the average change in velocity is towards the centre of the circle. This is always the case and thus true for instantaneous acceleration. This acceleration is called the centripetal acceleration .

Fig. 3. The direction of the change in velocity (and acceleration) is directed towards the centre of the circle.

For an object of mass , moving at a speed , in uniform circular motion of radius , the net force acting on is called the centripetal force and its magnitude is given by equation 1

(1) centripetal force

This centripetal force is responsible for the change in direction of the object as its speed is constant. The resulting acceleration due to the change in direction is the centripetal acceleration and its magnitude is given by equation 2. The direction of the centripetal force and centripetal acceleration is towards the centre of the circle (centripetal means centre seeking).

(2) centripetal acceleration

[WARNING: the equations given in the Physics Stage 6 Syllabus for the centripetal force and centripetal acceleration are absolutely incorrect]

It is important to understand that centripetal force is not a new force that starts acting on something when it moves in a circle. It is the sum of all forces acting on the object. This resultant force results from all the other forces on the object. When the rock in the example above is whirled in a vertical circle (instead of horizontal), gravity interacts with the tension in the string to produce the net force which we call centripetal force. Centripetal force is always the net force.

Predict / Observe / Explain: Circular Motion

Mathematical Analysis of Uniform Circular Motion

You do not need this depth of treatment for any examination. However, by understanding of the mathematics, you will gain a much deeper insight into circular motion. Richard Feynman one of the greatest physicists and teachers of the20th century, said that leaning was a creative process and one of the best approaches to learning physics was to start with first principles.

Our object is simply moving in a circle with a constant speed. So, we start with the equation of a circle and what we know about describing a moving object: time, displacement, velocity and acceleration.

The position of the object can be given as

As the object moves with uniform circular motion at a radius , it sweeps out an angle in a time interval . When , the instantaneous angular speed is

angular speed [rad.s^-1]

The arc length is the distance the objects moves in the time interval . The instantaneous tangential velocity of the object is ()

tangential velocity [m.s^-1]

This velocity is called the tangential velocity since at any instant the direction of the velocity vector is tangential to the circle.

The components of the position of the object at any instant are

The components of the tangential velocity at any instant are

The magnitude of the velocity is

The components of the centripetal acceleration at any instant are

The magnitude of the centripetal acceleration is

The direction of the centripetal acceleration is always directed towards the centre of the circle since

Note: A force must be applied to an object to give it circular motion. This net force is called the centripetal force.

Period, frequency, angular frequency (speed)

Consider an object executing uniform circular motion with a radius r and speed v . The time for one complete revolution is known as the period T . The distance travelled by the object in one period is simply the circumference of the circle . The orbit speed , period and radius are connected by the equations

The frequency f and angular frequency (speed) are

ENERGY and WORK

Have you wondered why the Earth just keeps going around the Sun year after a year, in fact for many billions of years the Earth has been orbiting the Sun. The Earth is attracted to the Sun by the gravitational force acting between the Earth and the Sun, but the Earth does not lose energy, it just keeps orbiting the Sun.

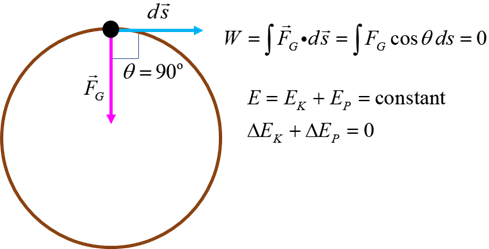
The gravitational force acts as the centripetal force responsible for the uniform circular motion of the Earth around the Sun (actually, the motion of the Earth is only approximately circular, and its speed does vary slightly in its orbit). The centripetal force always acts towards the centre of the circle, but at each instant the displacement of the Earth is at right angles to the centripetal force. Hence, zero work is done by the gravitational force and there is zero change in potential or kinetic energies of the Earth in its orbit and the total energy is constant. So, the Earth can just keep orbiting.

The work done by the net force on an object equals its change in kinetic energy. For uniform circular motion, the speed and hence kinetic energy do not change, Therefore, the net force (centripetal force) does zero work on the object.

Work done by the centripetal force

Note: The equation for angular speed given in the Physics Stage 6 Syllabus is . This expression should always be written as . This is another example of the incompetence of the people who put the Syllabus together.

VISUAL PHYSICS ONLINE

spHome.htm

Ian Cooper School of Physics University of Sydney

If you have any feedback, comments, suggestions or corrections please email Ian Cooper

ian.cooper@sydney.edu.au