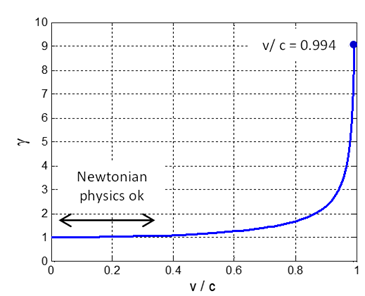
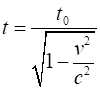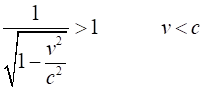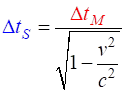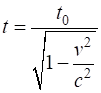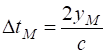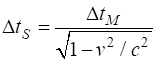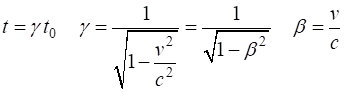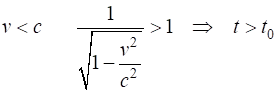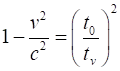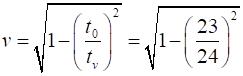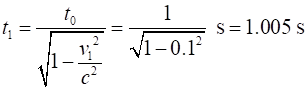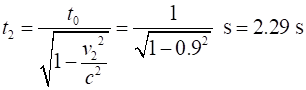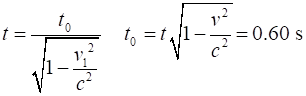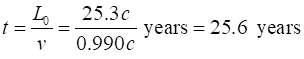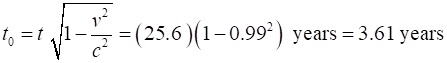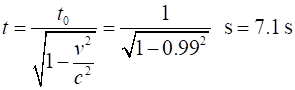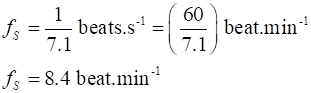|
LIGHT and SPECIAL
RELATIVITY TIME EVENTS SIMULTANEITY TIME DILATION EFFECT |
|
SUMMARY Time is a relative quantity: different observers can measurement different time intervals
between the occurrence of two events. This arises because the speed of
light is a constant and independent of the motion of the source of light or
the motion of an observer.
Moving clocks run slow Time Dilation Effect Proper time t0 – the
time interval between two events occurring at the same point in space w.r.t.
a clock at rest at that point. Dilated time interval t time
interval for event observed in a moving frame as measured on synchronised
clocks by a stationary observer. Twin paradox:
The twin who goes on a return space journey will return younger than the twin
who stayed on Earth.
Simultaneity: Two events that are simultaneous in
one frame of reference (S) are not
necessarily simultaneous in another frame of reference (M) moving with respect to the first frame (S). |
|
Learning strategies The
time dilation effect can be very confusing, even to physicists. So, we need a
strategy to overcome the difficulties to better understand and apply the
concepts associated with the time dilation effect. The way to approach the
time dilation effect is to recognise the fact that there are two frames of
reference moving w.r.t. to each other with a constant velocity. An easy way
to do this is to label the two frames of reference as Stationary or Fixed
(Steve) and Moving (Mary). · Steve: stationary (fixed) frame of reference · Mary: moving frame of reference (Mary’s
frame of reference is moving at a constant velocity An
event occurs in Mary’s frame of
reference and this event is observed by Steve
in his frame of reference. Mary measures the
duration time
(LS1) Equation
LS1 is the best way to think about the time dilation equation and this is the
format in which the equation is presented in better quality physics
textbooks. However, in the syllabus and not so good textbook, the equation
for time dilation effect is written as
(LS2) Equation
LS2 does not clearly differentiate between the two frames of reference and t is not time, but represents a
time interval measurement, so it better to use
|
|
SIMULANEITY Two events that
are simultaneous in one frame of reference (S) are not
necessarily simultaneous in another frame of reference (M) moving with
respect to the first frame (S) Einstein
recognised the fact that an event in a given system must be specified by
stating both its space and time coordinates, since both space and time are
not absolute but relative quantities. Consider
the flashing of two green bulbs fixed in
the Steve’s stationary frame of reference. The two bulbs are positioned
on either side of Steve at equal distances.
When the bulbs flash together, the light will travel equal distances and Steve will see the flashes arrive simultaneously
(the two flashes arrive at the same time). Mary
is moving at a constant velocity from the left to right past Steve. At the instant Mary is alongside Steve, the two green
bulbs flash. Remember, Steve says the two
light flashes arrive at the same time.
However, in the time for the light to arrive at Steve’s location, Mary
has moved to the right slightly, and she concludes that the light coming from
the right arrived before the light from the left since the light must travel
a greater distance from the left. The event was not simultaneous from Mary’s point of view (figure 1).
Fig. 1. Green flashbulbs are positioned in Steve’s frame at equal distances on either
side of Steve. According to Steve, since the
two pulses of green light arrive at the same time, the two bulbs went off
simultaneously. Mary in her frame is moving to
the right with constant velocity. The two bulbs flash when Mary and Steve are
abreast of each other. During the flight time of the light flashes, Mary has moved to the right, and hence the two
flashes do not arrive simultaneously. The light from the right travels a
shorter distance than the light coming from the left. Hence, Mary concludes the bulb on the right flashed before
the one on the left. The time interval between two events maybe different in different
frames of reference. RELATIVE TIME:
TIME DILATION In
the Theory of Special Relativity, time dilation is the actual difference of elapsed time between two
events as measured by observers in inertial frames of reference that are in
relative motion. We assume that there are no gravitational effects because
from the theory of General Relativity, clocks run slow in stronger
gravitational fields. This gravitational effect on time intervals must be
considered for GPS satellite systems. Clocks on the ground run slower than
clocks on board the GPS satellites.
http://en.wikipedia.org/wiki/Time_dilation Concise
Oxford Dictionary: dilate make or become wider or
larger; expand; widen; enlarge The
time interval for an event depends upon the relative motion between the
location of the of the event and the location of an observer. Different
observers may measure different time intervals. A time interval is a relative
quantity and not an absolute quantity. This effect arises neither from
technical aspects of the clocks nor from the fact that signals need time to
propagate, but from the nature of space - time itself. Consider
two inertial frames of reference. Steve’s
system is chosen as the stationary (fixed) reference frame and Mary’s system as moving along the X axis with
constant velocity v as shown in figure 2.
Think of Mary in a train carriage
moving past Steve who is standing on the
ground. As Mary passes Steve, a light is switch on in the train carriage and the light
travels from floor-ceiling-floor.
Our goal is to find the time interval for the light to travel from
floor-ceiling-floor as observed by Mary and Steve. Note: Steve
is in the stationary frame, while Mary is in
the moving frame and Steve observes the event
that occurs in Mary’s frame.
Fig. 2. Mary
is a moving train carriage (moving frame of reference) and Steve is standing on the ground (stationary frame
of reference) observing the event of a flash of light traveling from
floor-ceiling-floor occurring in Mary’s frame of reference. We will
assume that the height of the carriage is 10 m and Mary
velocity w.r.t. Steve is 0.8c. Mary: moving frame of reference The
event observed by Mary is a flash of light that travels at the speed of light
c from
floor-ceiling-floor as she passes Steve. The distance from the floor to the
ceiling is
Fig. 3. The time for
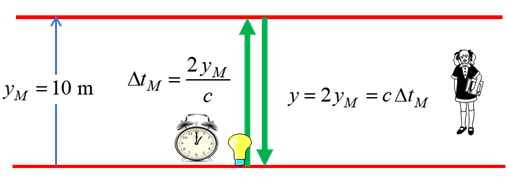
the round trip of the light is Steve: Stationary frame of reference Steve
observes the round trip for the flash of light that occurs in Mary’s
frame of reference. The event of the flash of light emitted from the floor
and the event of the light returning to the floor occur at two different
locations in Steve’s frame of reference. Therefore, two synchronized
clocks are required, one at each location of each event. When the flash of
light is emitted, the time on clock 1 is recorded and clock 2 records the
time at the end of the round trip for the light flash. The time interval
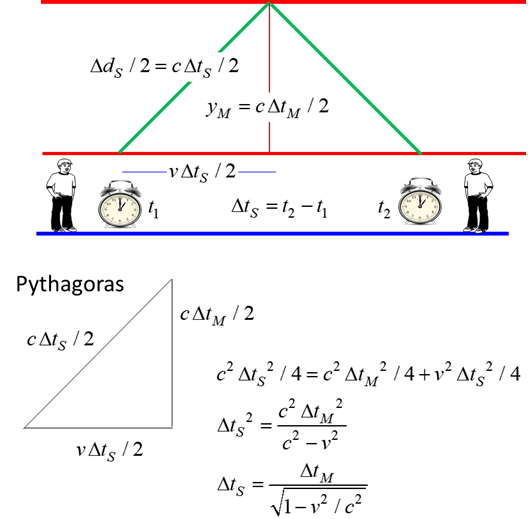
Fig. 4. The
path of the flash of light as observed by Steve. The distance travelled by
the light from Steve’s point of view is greater than from Mary’s
point of view. Therefore, the light must take longer for its round trip for
Steve then Mary. If
Fig. 5. Mary in her
frame observes the flash of light emitted from a source and reflected-back
along the same vertical straight line. However, Steve observes the same flash
of light travelling in straight lines which have both vertical and horizontal
components as shown. Steve measures a longer time interval Check the numbers Given speed
of light speed
of Mary w.r.t. Steve floor-ceiling
distance Calculations Distance
flash of travelled in Mary’s frame Time
interval in Mary’s frame
Distance
Mary’s carriage moved to the right in Steve’s frame Distance
flash of light travelled in Steve’s frame Time
interval in Steve’s frame Show
that the numbers agree with the prediction Time dilation equation
Syllabus equation
Fig. 6. There
is only one frame of reference in which a clock is at rest and the time
interval between two events occur at the same location. This time interval is
called the proper time The
moving clock can be any kind of clock. It can be the time for sand to move
through an hour glass, the time for a light to be switched on/off, the time
between heartbeats or the time between ticks of a clock. In the example shown
in figure 5, if Steve has aged by 111 years, he would observe a much younger
Mary who had aged only by 67 years. We
could repeat the calculation can take Mary’s system as fixed system and
Steve’s as the moving system and Mary would conclude that Steve’s
clock is running slow. Because of the symmetry, each person can claim the
clock in the other (moving) system is running slow Observers measure
any clock to run slow if it moves relative to them Time
dilation slows everything down literally everything (apart from light). All
cellular processes slow down, rate of hair growth slows down, cell
degeneration slows down, cell regeneration slows down and therefore ageing
slows down. Time
intervals aren't absolute. Different observers genuinely experience different
intervals of time, and there is no privileged observer that can claim to have
experienced the actual amount of time something took. The
time dilation effect must be taken into account in GPS since the communication
satellites involved are moving with respect to each to other with relative
speeds varying from 0 to
15.8km.s-1. These speeds are extremely small compared to
the speed of light. However, for accurate position determinations, the small
corrections due to the time dilation effect and general relativity effects
must be used.
Fig. 7. In a
GPS system both the effects of special relativity and general relativity must
be considered. |
|
Example 1 A
day on Earth has 24.00 hours. How fast must a rocket travel so that the
rocket’s clock measures a time interval of 23.00 hours? Solution How to approach the
problem (ISEE) Type of problem: special relativity / time
dilation Knowledge: moving clocks run slow
Data: Earth:
stationary system Rocket:
moving system Speed
of rocket system w.r.t. Earth system v =
? c Execute: (substitute
numbers into formula for time dilation)
v = 0.29 c |
|
Example
2 Consider
two trains with velocities v1 = 0.10c and v2 = 0.90c w.r.t. a stationary frame of
reference. In the stationary frame of reference, the duration of between two
events was 1.00 s. What would be the duration of the event as measured
by clocks on the trains? Solution How to approach the
problem (ISEE) Type of problem: special relativity / time dilation Draw an annotated
diagram – need to identify the systems in which the proper time
interval the dilated time are measured (it is not always easily to
distinguish the system for the proper time or dilated time). Knowledge: moving clocks run slow
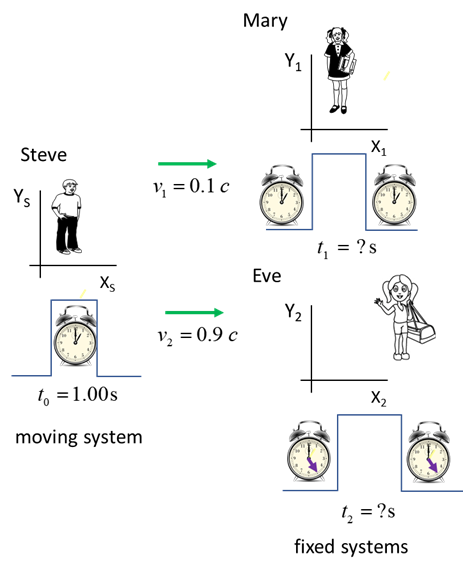
Let the inertial reference frames be identify as Steve’s
system, Mary’s system and Eve’s system. The event occurs in
Steve’s system, so, the proper time interval is t0 = 1.00 s. This event is observed
by Mary and Eve in their systems. So, Mary and Eve become the fixed system
and Steve’s system the moving system.
Steve needs only one clock to make the time interval measurement
since the event occurs at one point in space. Both Mary and Eve need two
clocks because the start and finish of the events occur at differential
special points. Proper
time t0 = 1.00 s Dilated time interval in Mary’s
system is
Dilated
time interval in Eve’s system is
The dilated time interval in Mary’s system (t1 = 1.005 s) is only slightly greater than the proper time (t0 = 1.00 s). However, the dilated time interval in Eve’s
system (t2 = 2.29 s)
is significantly larger than the proper time interval. It is essential that you understand that this is not an
illusion. It makes no sense to
ask which of these times is the “real” time. Since no preferred reference frame
exists all times are as real as each other. They are the real times seen for the
event by the respective observers. Time dilation tells us that a moving clock runs slower than a
clock at rest by a factor of
This result, however, can be generalised beyond clocks to
include all physical, biological and chemical processes. The Theory of Special Relativity
predicts that all such processes occurring in a moving frame will slow down
relative to a stationary clock. A time interval measurement is a relative quantity. So, if Mary
measured the time interval for an event occurring in Eve’s system as
1.005 s, what is the time interval measurement that would be measured by Eve? Mary Eve Speed of Eve w.r.t. Mary
|
|
TWIN PARADOX The
twin paradox is another example of a thought experiment in
relativity. Consider two
twins. Twin A takes a trip in a
rocket ship at speed v
relative to the Earth to a distant point in space and then returns, again at
the speed v. Twin B remains on Earth the whole
time. According to Twin B, the
travelling twin will have aged less, since his clock would have been running
slowly relative to Twin B’s clock and would therefore have recorded
less time than Twin B’s clock.
However, since no preferred reference frame exists, Twin A would say
that it is he who is at rest and that the Earth twin travels away from him
and then returns. Hence, Twin A
will predict that time will pass more slowly on Earth, and hence the Earth
twin will be the younger one when they are re-united. Since they both cannot be right, we
have a paradox. To
resolve the paradox, we need to realise that it arises because we assume that
the twins’ situations are symmetrical and interchangeable. On closer examination, we find that this
assumption is not correct. The
results of Special Relativity can only be applied by observers in inertial
reference frames. Since the Earth
is considered an inertial reference frame, the prediction of Twin B should be
reliable. Twin A is only in an
inertial frame whilst travelling at constant velocity v. During the intervals when the rocket
ship accelerates, to speed up or slow down, the reference frame of Twin A is
non-inertial. The predictions of
the travelling twin based on Special Relativity during these acceleration
periods will be incorrect.
General Relativity can be used to treat the periods of accelerated
motion. When this is done, it is
found that the travelling twin is indeed the younger one. Note that the only
way to tell whose clock has been running slowly is to bring both clocks back
together, at rest on Earth. It is
then found that it is the observer who goes on the round trip whose clock has
slowed down relative to the clock of the observer who stayed at home. This
has been confirmed by aircraft carrying clock’s around the Earth.
|
|
Example
3 Astronaut
Mary travels from Earth to Vega (5th brightest star in the night sky),
leaving her 30 year old twin brother Steve behind. Mary travels with a speed
0.990c and
Vega is 25.3 light-years from Earth (1 light-year is the distance travelled
by light in one year). At the end
of the journey by Mary, what is the age of the twins? During
the journey through space, Mary’s pulse rate was monitored.
Mary’s heart rate recorded on her monitor was 60 beats.min-1.
What heart rate was recorded on Steve’s monitor? Solution Think How to
approach the problem Visualise the physical
situation Annotated diagram
(known and unknown quantities, frames of reference Type of problem special relativity
time dilation Knowledge Mary:
moving frame of reference Steve:
fixed (stationary) frame of reference t Speed
of Mary w.r.t. Steve
The
event is the journey of Mary in the space ship from the Earth to Vega. In
Steve’s fixed frame, the Earth and Vega are stationary and Mary travels
the distance Mary
is in the moving frame and her clock records the proper time interval Thus,
when Mary reaches Vega, she is only 33.6 years old, but Steve who was left
behind on Earth is 55.6 years old. From
the point of view of Mary, the journey took 3.61 y at a speed of 0.990c. Mary
concludes that the distance L is known as the contracted length. Note:
Steve and Mary disagree on time interval and length measurements – time
and distance are a relative concept. Steve’s
fixed system t = 25.6 y L0 = 25.3 ly Mary’s moving system t0 = 3.61
y L = 3.57 ly Mary’s system Heart
rate Time
interval between pulses (proper time)
t0 = 1 / fM =
1 s Steve’s system Dilated
time Heart rate The rate of a person’s heartbeat
does not change because of time dilation. The rate at which another person,
moving relative to the first, measures the first person’s heartbeat
depends on their relative velocity. We conclude that Steve’s heart rate
is less than Mary’s heart rate. |