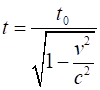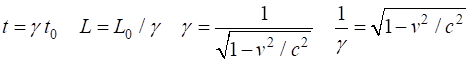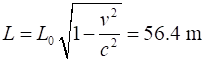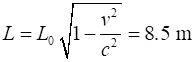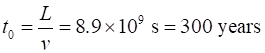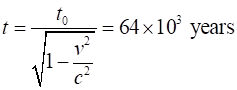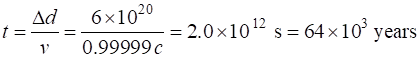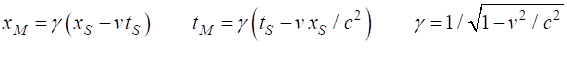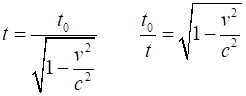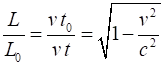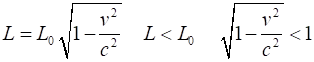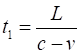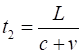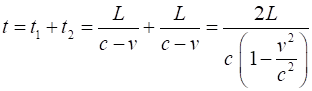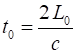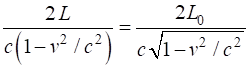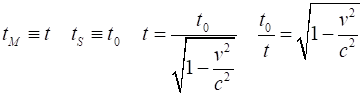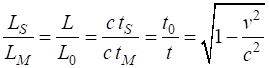|
LIGHT and SPECIAL
RELATIVITY LENGTH CONTRACTION |
|
SUMMARY Time is a relative quantity: different observers can measurement different time intervals
between the occurrence of two events. This arises because the speed of
light is a constant and independent of the motion of the source of light or
the motion of an observer.
Moving clocks run slow Time Dilation Effect Proper time t0 – the
time interval between two events occurring at the same point in space w.r.t.
a clock at rest at that point. Dilated time interval t time
interval for an event observed in a moving frame by a stationary observer as
measured their synchronised clocks. Lorentz-Fitzgerald Contraction Equation of a
moving object contracted
length L and
proper length L0 Contraction
takes place in the direction of motion only
|
|
Learning strategies The
way to approach the time dilation effect and the length contract effect is to
recognise the fact that there are two frames of reference moving with a
constant velocity w.r.t. to each other. An easy way to do this is to label
the two frames of reference as Stationary or Fixed (Steve) and
Moving (Mary). · Steve: stationary (fixed) frame of reference · Mary: moving frame of reference (Mary’s
frame of reference is moving at a constant velocity The proper length L0 is measured in the moving frame of reference and the constracted length L is
the length measured by the observer in the stationary frame of reference. |
|
LENGTH CONTRACTION Length is a
relative quantity When
measuring the length of an object it may be necessary measure the exact
position of its ends simultaneously. However, observers in different
reference frames may disagree on the simultaneity of two events. So, they may
also disagree about the length of objects. In turns out, the length of a
moving object appears to contract in the direction of motion relative to a
“stationary” observer. Equation
(1) is known as the Lorentz-Fitzgerald
Contraction Equation of a moving object (1) ·
Contracted length of object · Rest length or proper length of
object ·
Velocity v (magnitude) of the object
relative to the observer in the stationary frame of reference. Contraction takes place in the direction of motion only
You
are a stationary observer in an inertial frame of reference. A train was
initially at rest in your frame of reference and you measure its length.
However, when the train is in motion your measurement of its length is
shorter. There is a contraction in its length. The train is shorter in the
direction of motion, but just as high and wide as it was at rest as shown in
figure 1.
Fig.
1. How long is a train? It
depends on the relative motion of the observer and the train. This
is a real difference in length of the object when it is motion relative to an
observer. For a person in the train, there is no contraction in length. Figure
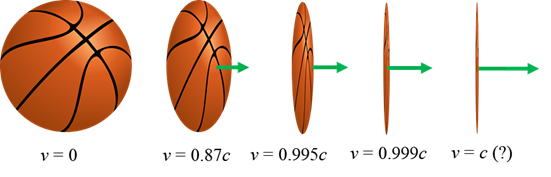
2 shows an animation of the length contract effect. Steve observers the rod
in his system as 80 m long. Steve observes the rod in moving frames of
reference to be shorter in length. The greater the velocity
Fig. 2. A
moving object is shorter to an observer in a stationary a stationary frame of
reference. The
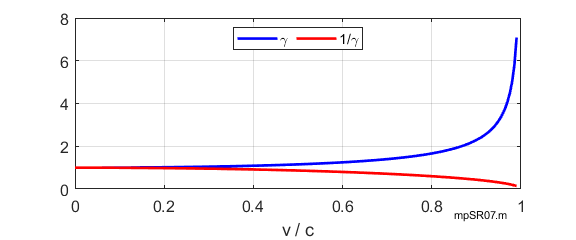
time dilation effect and the length contraction effect depend on velocity
Fig. 3.
Newtonian
principles can be applied when
As |
|
Example
1 A
spaceship flies past Earth at a speed of 0.990c. Mary on board the spaceship measures its length to be 400 m.
What is Steve’s measurement for the length of the spaceship on Earth? Steve
and Eve on Earth are standing 60 m apart as they view the passing spaceship.
How far apart are Steve and Eve from Mary’s point of view? Solution The problem
relates to the length contraction of a moving rod. Moving frame (Mary) Mary
in her system measures the proper length of the spaceship Stationary frame (Steve) Steve observes
the spaceship moving at uniform velocity v and
measures the length of the spaceship as L (contracted
length) Lorentz-Fitzgerald Contraction The
answer makes sense, the moving spaceship is observed to the shorter than in
the frame stationary w.r.t. to the spaceship. Moving frame (Steve and Eve) Steve
and Eve are at rest in the frame of the Earth. Their separation distance of
60 m is the proper length. Stationary frame (Mary) From Mary perspective, Steve and Eve
are moving at a speed v.
So, Mary will measure a contracted length L as the separation distance:
|
|
Example 2 The diameter of our galaxy is 6.0x1020 m. (a)
If the
speed of the spaceship was 0.99999c,
how long would it take to cross the galaxy as measured from the frame of
reference of the spaceship? (b)
How much
time would elapse on Earth for this journey across the galaxy? Solution (a) Relative velocity of moving frame w.r.t. stationary frame Stationary frame (Earth and Galaxy) proper length Moving frame (observer in spaceship) A traveller in the spacecraft would be at rest in the spaceship
and would see the galaxy approaching at speed v. The traveller would see the galaxy contracted in the direction
of motion. The contracted length L
is If the time t0 is measured in the spacecraft, the time for the journey across
the galaxy is t0 = ? s = ? years L = 2.7x1018 m
L = v t0 Even a spaceship travelling at speeds 0.99999c it still takes 300 years to cross
the galaxy. (b) Moving frame (observer in spaceship) proper
time Stationary frame (observer on Earth) An Earth bound observer will view the moving clock on the
spaceship and measure a dilated time interval dilated time interval for Earth observer t = ? years v = 0.99999c Alternative calculation for space ship to reach galaxy
WOW!!! For the Earth observer, 64 000 years
pass for the spaceship to cross the galaxy but on the spaceship only 300
years have passed. Only, spaceships travelling at speeds extremely close to the speed of light can traverse the huge astronomical distances need for space travel in “reasonable” times. |
|
Example 3 This problem is more difficult than you would normally encounter
at school. However, it is a very interesting one, and emphasizes some of the
important conceptual difficulties in special relativity. Reference: Modern Physics, J.R.
Taylor and C.D. Zafiratos A
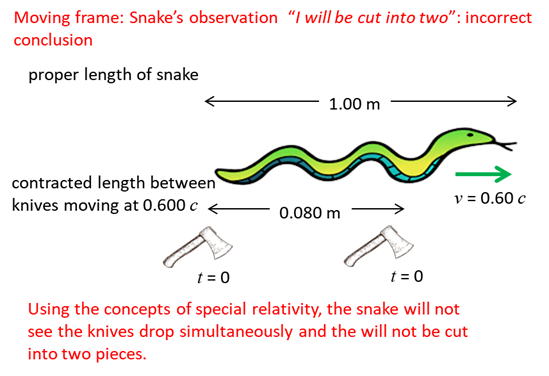
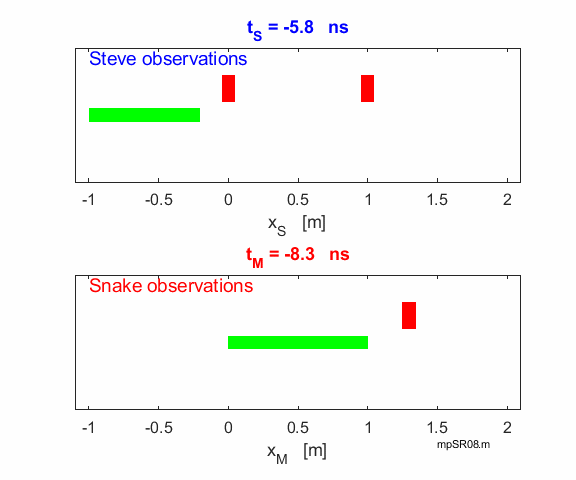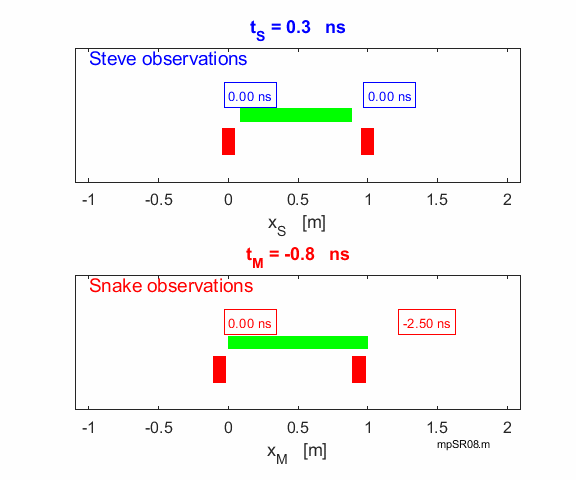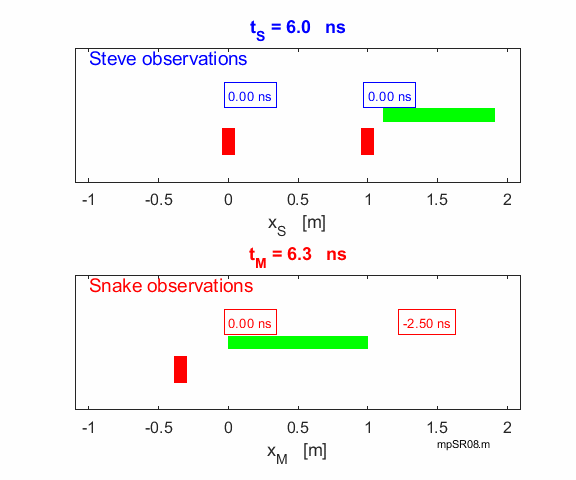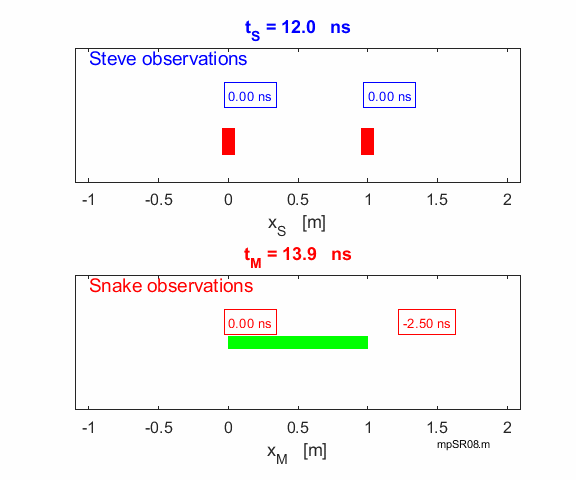
relativistic snake called Mary of proper length 1.00 m is moving at speed v = 0.60 c to the right across a table. Steve,
wishes to tease the snake, and holds two knives 1.00 m apart and plans to
bounce them simultaneously on the on the table so the left knife lands
immediately behind the snake’s tail. Steve argues as follows “The
snake (Mary) is moving with v = 0.60 c. Its contracted length is only 0.80 m
Therefore,
the right knife will land 0.20 m in front of the snake’s head, and the
snake will not be harmed.”
However,
Mary the snake argues, “the knives are approaching me at v = 0.60 c and the distance between them
is contracted to 0.80 m. So, I will be cut into two pieces when the knives
fall”. The
snake Mary and Steve cannot be both correct. The snake will or will not be
cut into two. We can resolve this paradox using special relativity. What
appears to be simultaneous in one frame of reference is not necessarily
simultaneous in another frame of reference.
In
Steve’s frame of reference, the snake is moving at speed v = 0.60 c and will observe the contraction
in the snake’s length. The two knives are stationary in Steve’s
frame. So, the statement that the two knives fall simultaneously at t = 0 is a correct. To
see what really happens, we need to examine the moving frame more carefully.
We now know that time and space are connected. The connection between time
intervals and spatial coordinates of two frames of reference (Stationary
and Moving)
is given by the equations (not in syllabus)
Stationary frame (Steve) Left-hand knife falls at Right-hand knife falls at Contracted length of snake Moving frame (Snake / Mary) Left hand knife falls at As expected, the left knife falls immediately besides the
snake’s tail at time Right-hand knife falls at position
Thus, the snake will observe that the two knives not falling
simultaneously, since the right knife falls 2.50 ns before the left knife.
Therefore, the right knife does not necessarily have to hit the snake, even
though the two knives are 0.80 m apart. We know the knife does miss the snake
because the right knife falls at 1.25 m well ahead of the snake’s head
as shown in the following animation.
The resolution of this paradox, and many similar paradoxes, is
seen to be that two events which are simultaneous as observed in one frame
are not necessarily simultaneous when observed in a different frame.
|
|
DERIVATIONS OF THE
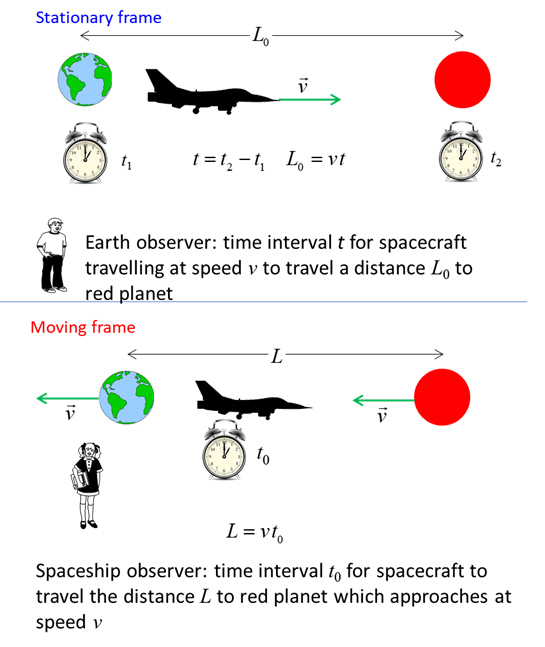
LENGTH CONTRACTION EQUATION (1) Consider a high-speed aircraft flying from the Earth to a planet
at a constant velocity
(Remember the definition of velocity in [1D]
Fig.
4. A length is measured to
be shorter when it is moving relative to the observer than when it is at
rest. Stationary frame (observer Steve on earth) Steve needs two clocks to measure the departure time Moving frame (observer Mary on aircraft) Mary
only need one clock to measure the time interval Hence,
using the dilation effect equation, we can derive the equation for length
contraction. Time dilation effect
Length contraction
(2) We
attach a laser to one end of a rod and a mirror at the other. The rod is at
rest in Mary’s system, and the length of the rod is L0 (proper length since it is at rest w.r.t observer
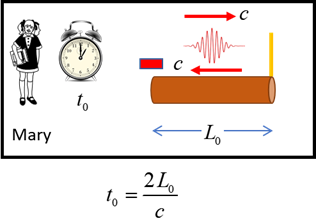
Mary). Moving system (Mary) Mary
measures a time interval t0 for a pulse of light to make the round trip from laser to
mirror and back. This is the proper time interval since the departure and
return occur at the same location in Mary’s system.
Fig. 5. The rod is
stationary in Mary’s system. The light pulse travels a distance L0 from the light source to the mirror. The time for the round
trip is t0. Stationary system (Steve) In
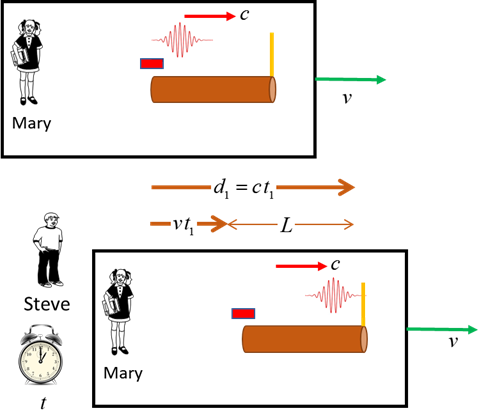
Steve’s system, the rod is moving to the right with constant speed v. Steve’s measures the
length of the rod as L and the time for the light to travel from laser to mirror as t1. During this time interval t1, the rod with laser and mirror attached moves a distance
Fig. 6. The rod is
moving to the right with constant speed v in Steve’s system. The light pulse travels a distance d1 from the laser to the mirror in time t1. The
total length of the path d1 from laser to mirror is therefore Note:
the division of L by c-u does not mean that light travels with speed c-u, but rather
the light pulse travels in Steve’s frame a distance greater than L. Repeating a similar calculation, the time interval t2 from the return journey of the light pulse from the mirror to
the laser is The
total time t for the for the round trip is The
proper time t0 and the dilated time t intervals
are connected by
Hence,
we can conclude
(3) There are two inertial frames of reference, Steve’s and
Mary’s. From Steve’s point of view, Mary’s frame in moving
with a constant velocity of magnitude v.
They both make measurements of the length of a rod. The rod is stationary in
Mary’s frame but moving with velocity v in
Steve’s frame. They both measure the length of the rod by observing the
time interval for a light pulse to travel from one end of the rod to the
other. They observe know that the speed of light is the same w.r.t both
frames of reference.
Distance measured by Mary is Distance
measured by Steve is So
far everything is straight forward, but now here comes the “tricky
part”. We must identify the proper and dilated time intervals and the
proper length and the contracted length. Steve’s
clock is stationary w.r.t. his frame, therefore, his clock records the proper
time and he view Mary’s clock which is the dilated time interval
Steve views the moving rod, so he measures the contracted
length, while the rod is stationary in Mary’s frame, so it is the
proper length
Length
contraction is real. This is not an optical illusion. The rod is really
shorter in Mary’s system than in Steve’s system. |
