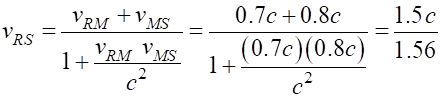|
LIGHT and SPECIAL
RELATIVITY RELATIVISTIC ADDITION OF
VELOCITIES A New Standard
of Length |
|
SUMMARY Relativistic addition of velocities
A New Standard of Length The speed of light by definition has the value 299 792 458 m.s-1 The
metre is now defined as the distance light travels in a vacuum in 1/299792458
of a second as measured by a caesium clock. |
|
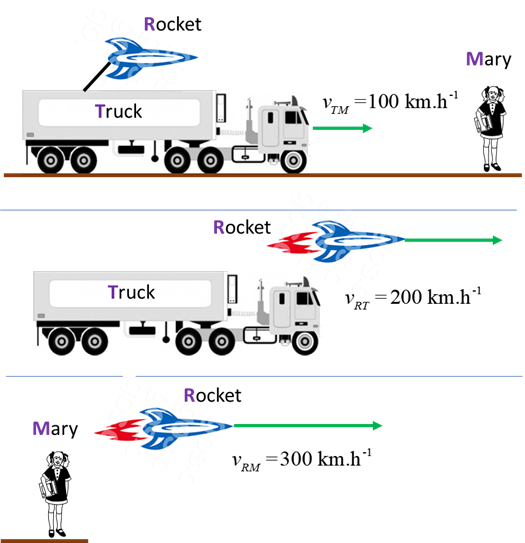
RELATIVISTIC ADDITION OF VELOCITIES A moving truck fired a rocket. The truck
was travelling at 100 km.h-1 and the rocket was launched with a
muzzle speed at 200 km.h-1 (speed of rocket w.r.t. truck) in the
same direction that the truck was moving. Obviously the speed of the rocket
is 300 km.h-1 w.r.t the ground
(100 + 200 = 300).
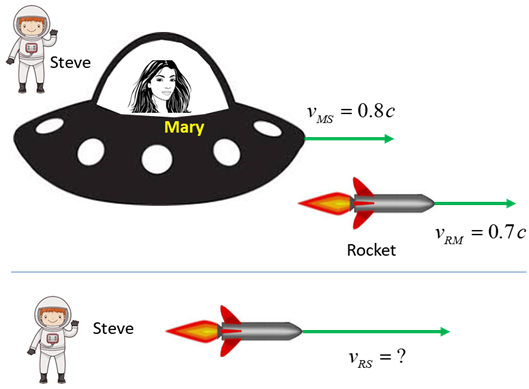
Fig. 1. Newtonian mechanics: adding velocities Mary is in a spaceship travelling at 0.8c w.r.t. Steve
Fig. 2. Addition of velocities. If According to Newtonian mechanics, the speed
of the rocket observed by Steve is But, our answer is wrong. We know that by Einstein’s
postulate that the speed of an object must be less than the speed of light c. Einstein derived the correct formula for
the addition of velocities. In our example, the velocity of the rocket w.r.t.
to the ground is (2) Applying the correction equation, the speed of the rocket w.r.t
Steve is
Note: if the speed of light were infinite A New Standard of Length
Length
is one of the fundamental quantities in Physics because its definition does
not depend on other physical quantities.
The SI unit of length, the metre was originally defined as one
ten-millionth of the distance from the equator to the geographic North
Pole. The first truly
international standard of length was a bar of platinum-iridium alloy called
the standard metre and kept in Paris.
The bar was supported mechanically in a prescribed way and kept in an
airtight cabinet at 0 oC. The distance between two fine lines
engraved on gold plugs near the ends of the bar was defined to be one metre. In
1961 an atomic standard of length was adopted by international agreement. The
metre was defined to be 1 650 763.73 times the wavelength of the orange-red
light from the isotope krypton-86.
This standard had many advantages over the original – increased
precision in length measurements, greater accessibility and greater
invariability to list a few. In
1983 the metre was re-defined in terms of the speed of light in a vacuum. The metre is now defined as the
distance light travels in a vacuum in 1/299792458 of a second as measured by
a caesium clock. Since the
speed of light is constant and we can measure time more accurately than
length, this standard provides increased precision over previous
standards. The reason for that
fraction (1/299792458) is that the standard then corresponds to the
historical definition of the metre – the length on the bar in Paris. So, our current standard of length is
defined in terms of time in contrast to the original standard metre, which
was defined directly in terms of length (distance). |