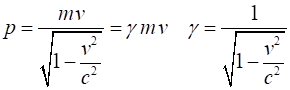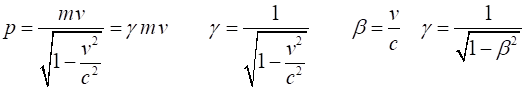VISUAL PHYSICS ONLINE

LIGHT and SPECIAL RELATIVITY

RELATIVISTIC MOMENTUM

SUMMARY

Einstein’s 1^st postulate states that the laws of physics are the same for all observers in all inertial frames of reference. So, the laws of conservation of momentum and energy applied to isolated systems must be valid in all inertial frames of reference.

Relativistic momentum

The mass of an object is taken as an intrinsic property of the object and is now considered an absolute quantity.

RELATIVISTIC MOMENTUM

Einstein’s 1^st postulate states that the laws of physics are the same for all observers in all inertial frames of reference. So, the laws of conservation of momentum and energy applied to isolated systems must be valid in all inertial frames of reference.

The relativistic momentum p of an object of mass m and moving with speed v w.r.t. to a fixed frame of reference is given by equation 1

(1)

The mass m in an intrinsic property of the object and is independent of the object’s velocity v.

The terms rest mass and relativistic mass were often used in the past. However, today, most research physicists prefer to keep the mass m of an object as an invariant (constant) quantity and thus can be considered as an absolute quantity. You should not refer to the terms rest mass and relativistic mass. All observers in all inertial frames of reference will measure the same value for the object’s mass.

Momentum is a relative quantity (like velocity), and so you always must know the frame of reference in which the momentum is measured.

As the speed v approaches the speed of light c, the relativistic momentum becomes significantly larger than the classical momentum, eventually diverging to infinity.

For low speeds v << c, the relativistic momentum and classical momentum agree p = m v.

An important consequence of the factor in the relativistic momentum equation (equation 1) is that no object can be accelerated past the speed of light. A constant force increases the momentum of an object at a constant rate. In classical physics, if the force acts for long enough, we can make the momentum and hence velocity as large as we please and greater than the speed of light c. In special relativity, an increase in momentum is reflected by increases in v and . Now as and we know that increases without limit. Thus, as the constant force keeps increasing without v ever reaching c.

Fig. 2. Classically (Newtonian Mechanics) the momentum increases in proportion to the speed. The correct relativistic momentum increases to infinity as the speed approaches the speed of light.

Example 1

A 1.00 kg object is observed to be traveling with speed 0.40 c. What is its momentum? What would be its momentum if its speed were doubled?

Relativistic answers

Note: the momentum increases by a factor greater 3 and not by a factor 2 as for the increase in speed.

Classical answers