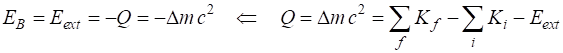|
SPECIAL RELATIVITY
and NUCLEAR REACTIONS
BINDING ENERGY |
|
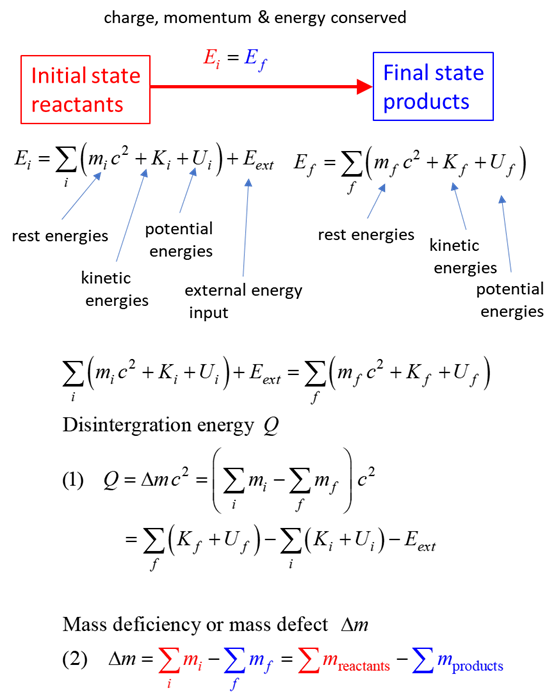
SUMMARY Total energy total
energy = rest energy + kinetic energy + potential energy
Law of
conservation mass-energy isolated
system E =
constant
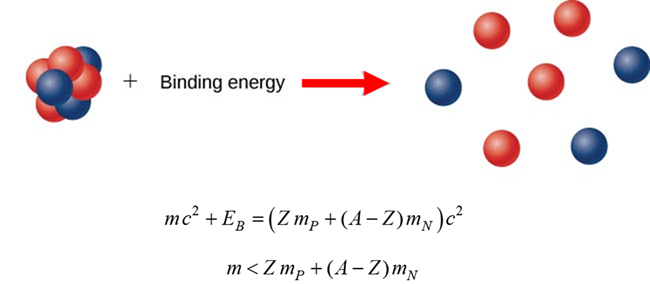
Binding Energy EB Nuclear binding energy EB is the
minimum energy that would be required to disassemble the nucleus of an atom
into its component parts. These component parts are neutrons and protons,
which are collectively called nucleons. |
|
Energy / Mass units, values and conversion factors amu (atomic mass unit) = 1 u = 1.66054´10-27 kg 1 eV = 1.602´10-19 J 1 MeV = 106 eV E = m c2
c = 2.99792´108
m.s-1
A mass of 1 u
(1 amu) has an energy equivalent of: E = (1.66054´10-27) (2.99792´108)2 J = 1.49242´10-10 J E = 931.494 MeV 1 u º 931.494 MeV/c2 Proton mass mp = 1.67262´10-27 kg = 1.0072765 u = 938.3 MeV/c2
Neutron mass mn =
1.67493´10-27 kg = 1.0086649 u = 939.6 MeV/c2 Electron mass me = 9.1093897´10-31 kg = 0.0005485799 u = 0.511
MeV/c2 BINDING ENERGY Nuclei are made up of protons and
neutrons, but the mass of a nucleus is always less than the sum of the
individual masses of the protons and neutrons which constitute it. The
difference is a measure of the nuclear binding energy which holds the nucleus
together. Nuclear binding
energy EB is the
minimum energy (work) required to pull the protons and neutrons out of the
bound state of the nucleus into separate free particles at rest. The forces that bind nucleons together in an atomic
nucleus are much greater than those that bind an electron to an atom through
electrostatic attraction. This is evident by the relative sizes of the atomic
nucleus (~10-15 m) compared with an atom (~10−10
m). So, the energy required to pry a nucleon from the nucleus is much larger
than the energy required to remove an electron from an atom (ionization). Consider the isotope AXZ which has Z protons (1H1)
and (A-Z) neutrons (1n0) in the nucleus where Z is the
atomic number and A is the mass number. The nuclear reaction to separate the
nucleus into its constituent protons and neutrons is AXZ and the Q-value
for the reaction is The binding energy is equal to the
negative Q-value
An important parameter describing a
nucleus is its binding energy per
nucleon Example 1 Binding
energy of the nucleus 4He2.
initial state (reactants)
4He2
Assume:
Atomic number Z = 2 Mass number A = 4 Number of neutrons A - Z = 2 Mass proton mP =
1.00727647 Mass neutronn mN = 1.00866492 Mass nucleus mNUC =
4.00150609 Mass defect
dm = -0.030377 u Q-value
Q = -28.2957 u Binding energy EB = 28.2957 MeV Binding energy / nucleon EB/A = 7.0739 MeV Q
<
0 implies the reaction is not spontaneous. Energy is required to pull the
nucleus apart. This energy EB is
called the binding energy. The binding energy is the work required to pull
the particles out of the bound state into separate free particles at
rest. Example 2 Binding energy 56Fe26
initial state (reactants)
56Fe26 Assume:
Atomic number Z = 26 Mass number A = 56 Number of neutrons A - Z = 30 Mass proton mP =
1.00727647 Mass neutronn mN = 1.00866492 Mass nucleus mNUC =
55.92067328 Mass defect
dm = -0.528462 u Q-value
Q = -492.2596 u Binding energy EB = 492.2596 MeV Binding energy / nucleon EB/A = 8.7903 MeV This isotope iron-56 is one of the most stable nuclei since its binding energy per nucleon is one of the highest values of any isotope. Example 3 What is the mass defect and binding energy of a deuteron nucleus 2H1 ? Mass
of deuteron nucleus 2.014186
u Mass of proton
1.007593 u Mass of neutron
1.008982 u Mass
(proton + neutron)
2.016575 u
Mass of nucleus is less than the constituent
nucleons.
Mass of deuteron nucleus (2.014186 u) < mass proton + neutron
(2.016575 u) Mass defect
Dm = (2.016575 - 2.014186) u = 0.002389 u This mass defect is responsible for the energy that
enables the nucleus to “stick together”. The binding energy EB of the deuteron is EB = Dm c2 =
(0.002389)(1.660x10-27)(3.0x108)2 J = 3.57x10-13 J EB = (3.57x10-13 / 1.602x10-19) eV = 2.22x106 eV =
2.22 MeV 1
amu = 1 u = 1.660x10-27 kg c = 3.0x108 m.s-1 qe =
e = 1.602x10-19 C
1 eV = 1.602x10-19
J 1
u = 931 MeV/c2 Alternatively EB =Dm c2 =
(0.002389)(931)c2 MeV/c2
= 2.22 MeV This number is confirmed by experiments that show that the minimum energy of a gamma ray must be greater than 2.22 MeV to disrupt a deuteron nucleus. Over two million electron volts are needed to break apart a deuteron into a proton and a neutron. This very large value indicates the great strength of the nuclear force. By comparison, the greatest amount of energy required to liberate an electron bound to a hydrogen atom by the electromagnetic attractive Coulomb force is about 10 eV. BINDING ENERGY PER NUCLEON The binding energy of the nucleus is the energy
needed to separate the nucleus into its constituent parts. If we take the total binding energy of
a nucleus and divide it by the total number of nucleons in the nucleus, we
get a very good measure of how tightly each individual nucleon is held in the
nucleus. This binding energy per
nucleon figure is a very good measure of the stability of a nucleus. The higher the binding energy per
nucleon, the more stable the nucleus.
Note that the binding energy per nucleon is low for low mass number
nuclei. This is because in such
nuclei each nucleon is not uniformly surrounded and thus does not experience
the full effects of the strong nuclear force. Most nuclei have binding energy
per nucleon values between 7 and 9 MeV, with the highest value being that for
56Fe26. For
very high mass number nuclei, the electrostatic repulsive forces between the
protons result in a gradual decrease in binding energy per nucleon values.
Fig. 1. Binding
energy per nucleon for stable nuclei. Figure 1 shows a very interesting curve when we plot the binding energy per nucleon (EB / A) vs mass number A of the nucleus. The curve is surprising regular in shape except for the peak for 4He2. The middle range nuclei have the highest binding energy per nucleon (~ 8.8 MeV / nucleon) and therefore the most stable. The higher the binding energy per nucleon, the more stable the nucleus. When a heavy nucleus is split into two lighter ones, a process called fission occurs and energy is liberated. When two very light nuclei join to form a heavier one, a process called fusion occurs and energy is liberated. For example, when two deuteron nuclei 2H1 + 2H1 to combine to give a helium nucleus 4He2, the energy liberated is about 23 MeV for this single nuclear reaction. The graph in figure 1 implies that nuclei divided or combined release an enormous amount of energy. This is the basis for a wide range of phenomena, from the production of electricity at a nuclear power plant to sunlight. |
|
|