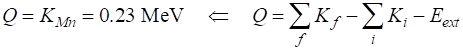Visual Physics

SPECIAL RELATIVITY and NUCLEAR REACTIONS

RADIOACTIVITY: BETA DECAY

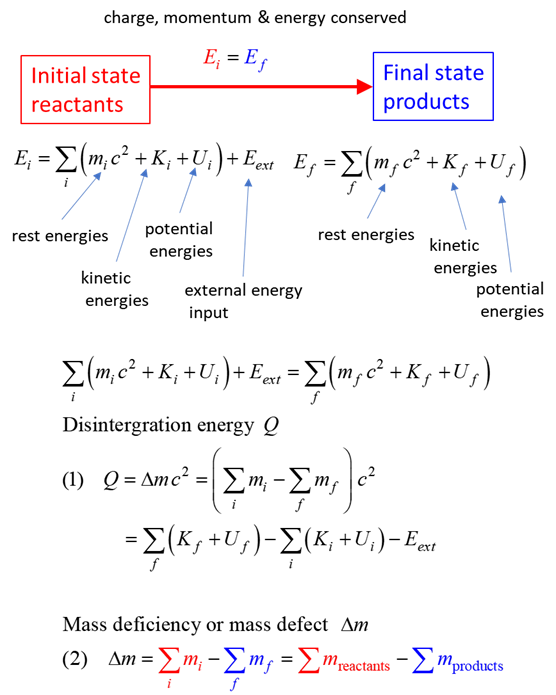
SUMMARY

Total energy

total energy = rest energy + kinetic energy + potential energy

Law of conservation mass-energy isolated system E = constant

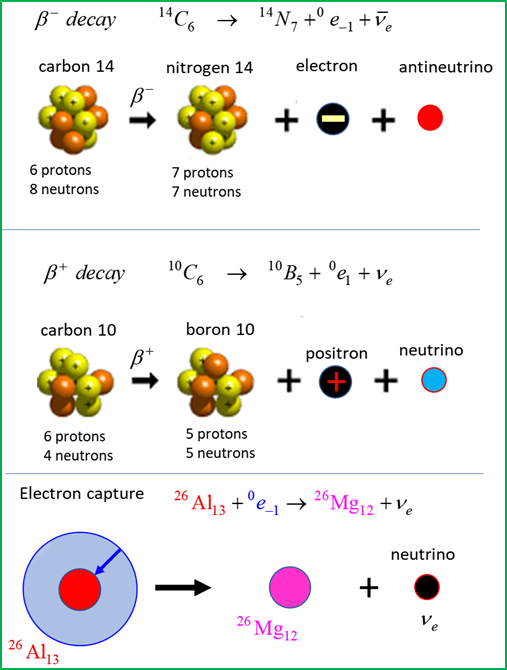
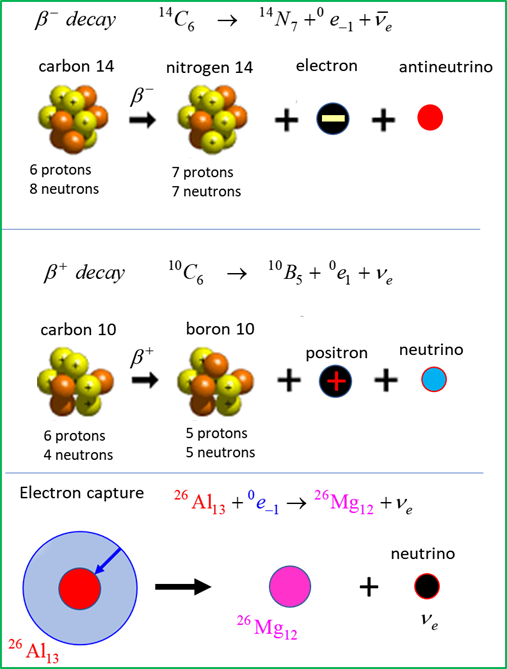
BETA DECAY

Beta decay is one process that unstable atoms can use to become more stable. There are two types of beta decay, beta-minus and beta-plus .

Beta-minus decay: a neutron in an atom's nucleus turns into a proton, an electron and

an antineutrino

Beta-plus decay: a proton in an atom's nucleus turns into a neutron, a positron and an

neutrino

Electron capture is one process that unstable atoms can use to become more stable. During electron capture, an electron in an atom's inner shell is drawn into the nucleus where it combines with a proton, forming a neutron and a neutrino. The neutrino is ejected from the atom's nucleus.

Energy / Mass units, values and conversion factors

amu (atomic mass unit) = 1 u = 1.66054´10^-27 kg

1 eV = 1.602´10^-19 J 1 MeV = 10⁶ eV

c = 2.99792´10⁸ m.s^-1

A mass of 1 u (1 amu) has an energy equivalent of:

E = (1.66054´10^-27) (2.99792´10⁸)² J = 1.49242´10^-10 J

E = 931.494 MeV

1 u º 931.494 MeV/c²

Proton mass

m_p = 1.67262´10^-27 kg = 1.0072765 u = 938.3 MeV/c²

Neutron mass

m_n = 1.67493´10^-27 kg = 1.0086649 u = 939.6 MeV/c²

Electron mass

m_e = 9.1093897´10^-31 kg = 0.0005485799 u = 0.511 MeV/c²

NUCLEAR REACTIONS

BETA DECAY

Suppose now that a nucleus exists which has either too many or too few neutrons relative to the number of protons present for stability. Stability can be achieved by the conversion inside the nucleus of a proton into a neutron or a neutron into a proton. In this transmutation:

Charge is conserved a beta particle is emitted from the nucleus

Energy and momentum are conserved a particle called a neutrino / antineutrino must also be emitted from the nucleus. Greek letter nu ()

Beta rays are more penetrating than alpha rays and move at a very high speed.

decay N / Z too large: neutron proton

The electron emitted in decay is not an orbital electron. The electron is created in the nucleus itself. We use the term particle for the electron to show its origin, nonetheless it is

indistinguishable from an orbital electron. The symbol represents the particle called the electron antineutrino (antiparticle of the electron neutrino).

A free neutron can also decay but not a free proton (on average a free neutron at rest lives for ~15 minutes)

decay N / Z too small: proton neutron

To conserve charge, the beta particle emitted is the positron . The positron is identical to an electron except that its charge is positive and is the antiparticle of the electron. In this

transmutation, an electron neutrino is also emitted.

Electron capture

Besides and emissions, there is a third process called electron capture and occurs when a nucleus captures (absorbs) one of its orbiting electrons

THE NEUTRINO

In beta decay, a more stable nucleus is produced and hence in the process energy is liberated as kinetic energy of the products. It was first envisaged that the products of beta decay were the only the daughter nucleus and an electron. Since daughter nucleus has a mass much larger than that of an electron it would recoil only very slowly with small energy whereas the electron would gain most of the energy liberated. 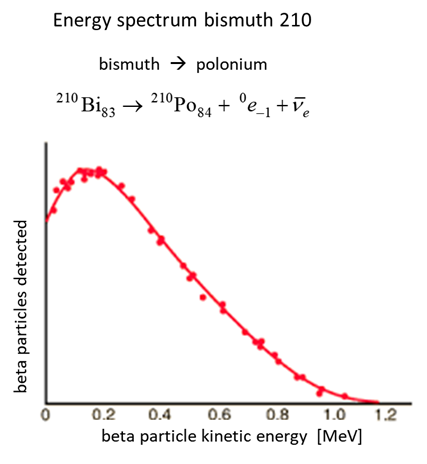Hence, it was expected that the emitted electrons in beta decay would have a fixed kinetic energy in each beta decay transmutation. But it was found experimentally that the kinetic energy of the emitted electron could have any value from zero up to the maximum value. It was if the law of conservation of energy was violated. Careful measurements indicated that linear and angular momentum were also not conserved.

Figure (1) shows the energy spectrum for the decay of bismuth into polonium.

Fig. 1. Beta decay of bismuth-210 into polonium-210 where a neutron changes into a proton.

The need to account for the energy distribution of electrons emitted in beta decay (figure 1) and to satisfy the laws of conservation of energy, linear and angular momentum, Austrian physicist Wolfgang Pauli in 1930 proposed that a neutral particle was emitted along with the particle. This particle would have no charge and zero rest mass (hence, travel at the speed of light) but would possess spin, energy and momentum. For each beta emission, the total energy carried away from the decaying nucleus would be shared between the beta particle and the neutral particle emitted with it. Hence, it would be expected that the beta particles emitted would have a range of energies depending on the energies of the neutral particles emitted with them.

In 1934, Italian physicist Enrico Fermi (1901 - 1954) named Pauli’s particle the neutrino (), meaning “little neutral one”in Italian, and formulated a theory of decay using this particle. Fermi’s theory successfully explained all experimental observations. For instance, the shape of the energy curve shown in figure (1) for Bi-210 can be predicted from the Fermi Theory of beta decay.

Despite several ingenious attempts, the neutrino was not experimentally observed until 1956. In that year, two American Physicists, Cowan and Reines successfully identified the neutrino by detecting the products of a reaction that could only have been initiated by the neutrino.

It was Fermi who, in this theory postulated the existence of the fourth force in nature: the weak nuclear force. In beta decay, it is the weak nuclear force that plays the crucial role. decay is often referred to as the weak interaction because it is 10¹² times weaker than the strong nuclear force that holds the nucleus together. The neutrino is unique in that it interacts with matter only via the weak nuclear force, which is why it is so hard to detect.